从整数阶微积分到分数阶微积分

宋超



从整数阶微积分到分数阶微积分

宋超

（南京工程学院 数理部，江苏 南京 211167）

分数阶微积分理论及其工程应用已经成为科研工作者关注的热点课题之一．从经典的整数阶积分和导数的定义谈起，简要介绍了如何从整数阶微积分的概念推广到一般的分数阶微积分及其分数阶微积分的基本性质．

整数阶微积分；分数阶微积分；分数阶微积分的性质

作为一门古老的学科，分数阶微积分已有300余年的发展历史，它最早出现在1695年9月30日Leibniz的日记中，其诞生几乎与整数阶微积分同步，但由于缺少实际应用背景，长期以来发展缓慢[1-2]．分数阶微积分准确地理解应该为非整数阶微积分，它是整数阶微积分的推广，其阶数不局限于整数而可为任意复数，它实现了连续阶微积分，从而扩展了整数阶微积分的功能．由于分数阶导数包含了从初始时刻开始到当前时刻的所有信息（整数阶导数只包含了当前时刻附近的信息），因而可以更加真实地刻画实际物理系统．分数阶系统和经典的整数阶系统相比，最大的优点在于可以描述各种物质及其演化过程的记忆和继承的性质，而在整数阶系统中这些性质都被忽略了．已有的研究表明，分数阶模型包含了经典的整数阶情形，而整数阶的情形可以作为分数阶情形的特殊情况．正因为有了如此强大的应用前景，分数阶微积分才重新回到人们的视野，受到来自各个领域学者的广泛关注，成为国际上的热点研究课题之一[3-4]．从整数阶微积分讲起，一步一步推广到分数阶微积分，并简单地介绍了分数阶微积分的基本性质，为认识分数阶微积分的发展脉络和应用提供了必备的基础知识．

1　从整数阶积分到分数阶积分

2　从整数阶导数到分数阶导数

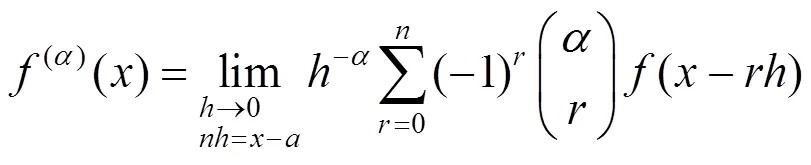
容易看出对于常数而言，它的Riemann-Liouville导数不为零，这与经典的常数的一阶导数为零相矛盾．并且实际中Riemann-Liouville分数阶微分方程的初值不易给出，它的Laplace变换较繁琐复杂，于是有了另外一种常见的分数阶导数——Caputo导数，其定义为[7]

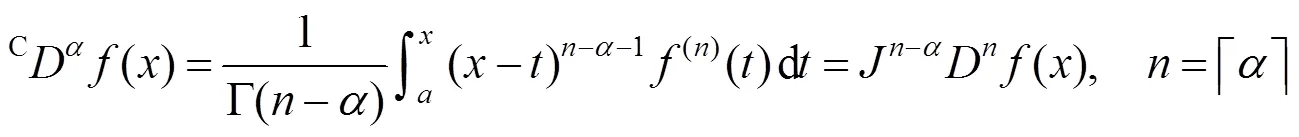
性质2无论是Riemann-Liouville导数还是Caputo导数，一般情形下，不成立，其中：．

3　结束语

分数阶微积分已在自然和社会科学的各个领域得到了广泛的关注和应用，它正在影响和改变人们的思维方式[8]．也许不久的将来，分数阶微积分理论将进入到大学数学的教材中，成为大学生所熟悉的工具．

[1] Cafagna D．Past and present-fractional calculus：A mathematical tool from the past for present engineers [J]．IEEE Industrial Electronics Magazine，2007，2（1）：35-40

[2] Ma C，Hori Y．Fractional-order control：theory and applications in motion control：past and present [J]．IEEE Industrial Electronics Magazine，2007，1（4）：6-16

[3] Ortigueira M D．An introduction to the fractional continuous time linear systems：The 21st century systems [J]．IEEE Circuits and Systems Magazine，2008，8（3）：19-26

[4] West B J．Colloquium：Fractional calculus view of complexity：A tutorial[J]．Reviews of Modern Physics，2014，86（4）：1169

[5] Diethelm K．The Analysis of Fractional Differential Equations--An application-oriented exposition using differential operators of Caputo type[M]．NewYork：Springer，Lecture Notes in Mathematics，2010

[6] Podlubny I．Fractional differential equations： an introduction to fractional derivatives，fractional differential equations，to methods of their solution and some of their applications[M]．SanDiego：Academic press，1998

[7] Kilbas A A A，Srivastava H M，Trujillo J J．Theory and applications of fractional differential equations[M]．Amsterda：Elsevier Science B V，2006

[8] West B J．Fractional Calculus View of Complexity：Tomorrow′s Science[M]．Florida：CRC Press，2015

From integer-order calculus to fractional-order calculus

SONG Chao

（Department of Mathematics and Physics，Nanjing Institute of Technology，Nanjing 211167，China）

The theory of fractional calculus and its engineering applications have become one of the hot topics for researchers．From the definition of the classical integer-order integral and derivative，briefly introduces how to generalize from the concept of integer-order calculus to general fractional-order calculus and basic properties of fractional calculus．

integer-order calculus；fractional-order calculus；basic properties of fractional calculus

1007-9831（2016）09-0015-03

O172

A

10.3969/j.issn.1007-9831.2016.09.005

2016-05-12

南京工程学院校级高等教育研究立项课题（2015ZC14）

宋超（1980-），男，山东临沂人，讲师，博士，从事分数阶系统理论及其应用研究．E-mail：chaosong@njit.edu.cn