干扰条件下MIMO雷达收发联合方向图优化设计

王玉玺 黄国策 李 伟



干扰条件下MIMO雷达收发联合方向图优化设计

王玉玺*黄国策 李 伟

(空军工程大学信息与导航学院 西安 710077)

针对干扰条件下MIMO雷达面临的信号截获以及干扰源快速移动等问题，对雷达收发方向图进行优化设计。在发射端利用最小积分旁瓣准则对发射波束矩阵进行优化，将发射信号能量集中到目标空域，降低旁瓣并在干扰方向形成发射零陷；在接收端利用广义对角加载方法优化接收方向图，在提高信号接收稳健性的同时展宽零陷。通过对MIMO雷达收发方向图进行联合优化设计，解决了信号被截获及快速移动的有源干扰等问题，从收发两端共同提高雷达整体性能。通过实验仿真对比分析，验证了所提方法的可行性和有效性。

MIMO雷达；方向图设计；稳健波束形成；零陷展宽

1 引言

近年来，集中式多输入多输出(Multiple Input Multiple Output, MIMO)雷达凭借能够发射不同波形的优异性能受到广泛关注。现有文献大都针对理想情况下MIMO雷达性能及应用进行研究。随着电子战技术快速发展，针对雷达的电子侦察和干扰方法越来越多，特别是机载干扰吊舱等干扰平台的使用，干扰方不仅具有高速机动的特点而且能够集侦查干扰于一体，根据对目标雷达信号的截获分析情况，灵活实施阻塞式或欺骗式干扰，使得雷达在战场中所面临的生存和工作环境越来越严峻。针对高速、智能化的敌方干扰，如何提高己方MIMO雷达的抗干扰能力成为目前极为迫切的研究问题。

传统集中式MIMO雷达，每个阵元通过发射相互正交信号，发射端发射功率在空间均匀分布，接收端通过波形匹配获得较大的虚拟阵列孔径，获得发射波形分集增益。但是在实际的MIMO雷达目标跟踪过程中，由于目标方向大致已知，全向的发射方向图不仅造成虚拟阵列每个阵元等效接收的信号强度较弱，而且增强了杂波信号，造成发射功率的浪费。针对该问题，人们利用MIMO雷达发射信号协方差矩阵秩大于1的特性，通过较大的发射波形自由度，来设计满足实际需求的发射方向图。文献[1]针对MIMO雷达发射方向图匹配问题提出了半正定二次规划方法(Semidefinite Quadratic Programming, SQP)，针对给定的发射方向图，利用最小二乘准则得到全局最优的发射信号相关矩阵；文献[2]将MIMO雷达发射方向图设计分为两步，首先利用约束优化得到满足要求的信号相关矩阵，然后根据相关矩阵求解具体的发射信号；文献[3]则提出了两种不同的基于凸优化的MIMO雷达发射信号相关矩阵的设计方法。虽然上述方法理论上能够得到与目标相匹配的发射方向图，但是由给定的信号相关矩阵求解具体满足要求的信号波形目前仍然较为困难，为了避免这一问题，文献[4]将信号相关矩阵优化问题转化为发射波束矩阵的优化，利用波束矩阵将方向图设计和波形设计分离；文献[5]则在此基础上进一步优化波束矩阵，使得由发射加权向量处理后的信号导向矢量具有旋转不变性；文献[6]将MIMO雷达发射方向图设计从空间和时间上解耦合，将问题转化为每个正交信号的波束形成问题，从而降低设计复杂度。同时，围绕MIMO雷达的信号接收，文献[7,8]分别设计了不同的稳健波束形成方法，提高了MIMO雷达在非理想情况下信号的接收性能。文献[9,10]则对干扰条件下的MIMO雷达稳健波束形成方法进行了研究。上述各种方法针对MIMO雷达仅从发射或接收方向图进行了单独的研究，文献[11-14]则在目标期望信号和杂波干扰方向已知的情况下，从发射端优化发射方向图抑制杂波干扰，实现了收发联合方向图的优化设计。但是在具体的对空警戒雷达等实际应用中，杂波对于目标跟踪性能的影响可以忽略，文献[10-14]所提方法仅对杂波抑制有效而且形成的零陷较窄，无法有效抵抗快速机动的敌方对己方雷达信号的截获和干扰。结合MIMO雷达实际应用中所存在的各种误差等非理想情况，以及电子战条件下雷达所可能面临的各种电子干扰，从收发双方联合优化设计MIMO雷达方向图，提高系统战场生存能力及整体工作性能，具有更好的实际应用价值。

本文针对干扰条件下，目标跟踪中MIMO雷达的收发联合方向图进行优化设计。在发射端通过利用最小旁瓣积分准则对发射波束矩阵进行优化设计，不仅避免了传统发射方向图优化设计中所存在的由给定相关矩阵求解具体信号的问题，而且降低了发射旁瓣，并利用先验信息在干扰方向上形成具有一定宽度的发射零陷，从而降低雷达信号被截获的概率。在接收端，针对现有的自适应接收波束对误差较为敏感、干扰零陷较窄等问题，利用非均匀广义对角加载的方法进一步提高接收端接收波束的稳健性并展宽零陷，从而能够有效抑制快速移动的有源干扰。通过对干扰条件下对MIMO雷达的收发方向图进行联合优化设计，从整体上提升MIMO雷达系统性能。

2 MIMO雷达信号模型

设由个阵元组成的收发共置集中式MIMO雷达，阵元间距为，第1个阵元为参考阵元，第个阵元发射信号为。远场方向处目标接收到的信号为

(2)

(4)

MIMO雷达发射信号在目标处功率为

(7)

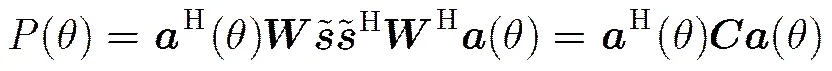
3 干扰条件下MIMO雷达发射方向图设计

MIMO雷达在目标跟踪过程中，由于目标大致方向已知，为提高目标跟踪精度，降低杂波信号强度，发射端需要将发射信号能量聚集到一定的空域范围内，同时在电子战环境中，为了防止敌方截获雷达信号进行欺骗式干扰或反辐射导弹攻击，需要在特定方向上形成零陷。针对该问题，本节首先对基于离散扁长椭圆序列(Discrete Prolate Spheroidal Sequences, DPSS)发射方向图进行零陷设计[4]，并针对该方法存在的方向图旁瓣较高的问题，结合实际应用中衡量旁瓣的积分旁瓣电平指标，利用凸优化方法设计一种新的基于最小积分旁瓣电平的MIMO雷达发射方向图。

3.1 干扰条件下DPSS发射方向图设计

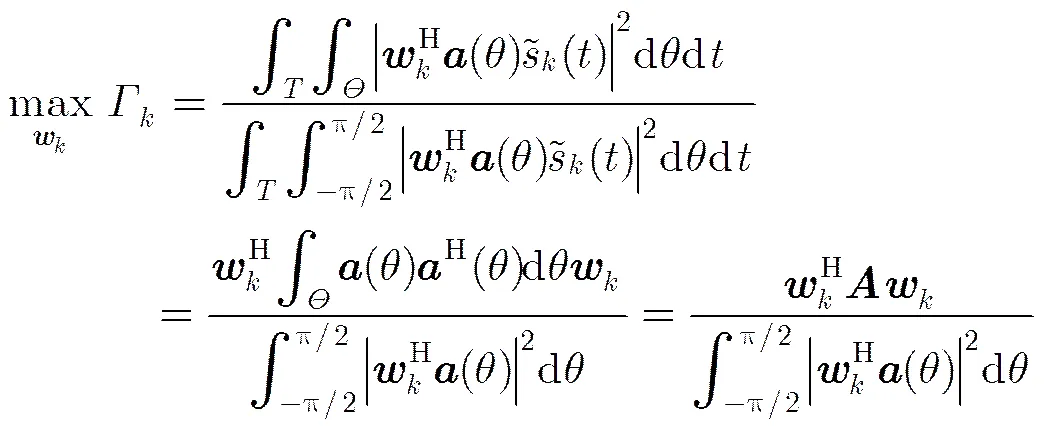
(10)

将式(10)代入式(9)可得

由式(11)可以看出，为了使信号能量尽可能集中在目标空域内，则应取为矩阵最大特征值所对应的特征向量，同时为了保证发射端的波形分集增益，需要满足,。因此最优发射波束矩阵为

(12)

计算干扰目标的正交投影矩阵为

(14)

则带有零陷的波束加权矩阵为

基于离散扁长椭圆序列的MIMO雷达发射方向图，当基带信号数目一定且发射阵元数目较少时，矩阵特征值分布相对均匀，会造成发射方向图旁瓣升高，杂波信号增强，进而影响雷达系统性能。而且通过利用干扰目标正交投影矩阵所得的波束加权矩阵所形成的发射方向图零陷较窄，因此具有高机动特性的干扰源有可能移出发射零陷并截获己方雷达信号。

3.2 干扰条件下最小积分旁瓣发射方向图设计

在实际应用中，旁瓣抑制不但可以将发射信号能量聚集在目标空域，而且能够减少来自旁瓣区域的杂波以及虚假目标的反射信号能量。本节结合实际应用中作为衡量旁瓣的积分旁瓣电平这一指标，同时针对机载干扰吊舱等集侦查和干扰于一体的快速机动干扰源，通过凸优化方法设计具有较低旁瓣和较宽零陷的发射方向图。干扰条件下最小积分旁瓣发射方向图设计模型为

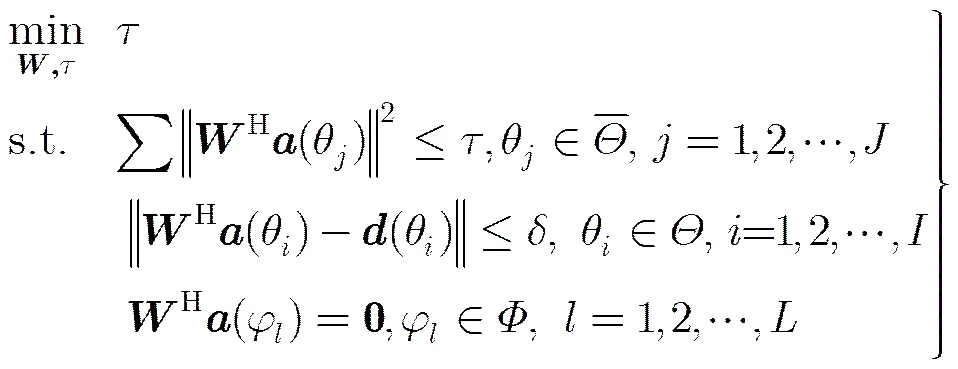
与现有的发射方向图根据功率匹配的设计思想不同，该方法利用发射波束矩阵，发射方向图由每个基带信号的发射波束合成这一性质[4]，将阵列发射信号导向矢量在目标空域内与期望信号导向矢量匹配作为约束条件，积分旁瓣作为目标函数，不仅避免了传统方法由信号协方差矩阵求解信号波形的问题，而且避免了由发射波束相关矩阵求解发射波束矩阵时所需要的向量随机化问题[5]，通过对优化后的发射加权矩阵进一步归一化处理，满足实际应用中发射总功率一定的约束条件，同时利用虚拟干扰思想，灵活展宽发射方向图零陷宽度，使敌方始终处于零陷之内，以降低雷达信号被截获侦查的概率。

4 干扰条件下MIMO雷达稳健接收方向图设计

由式(4)可知，MIMO雷达接收端接收到的信号为

(18)

对角加载算法[15]作为一种最为简单有效的稳健波束形成算法受到人们关注，该方法通过人为注入白噪声，一方面通过降低快拍数据中信噪比，减轻了期望信号导向矢量失配对波束形成质量的影响；另一方面通过人为增加噪声功率，解决了因快拍次数较小而造成的噪声子空间特征值发散，降低了噪声对波束形成的影响并提高了算法收敛速度，但是该算法存在对角加载因子固定且加载电平不易确定的问题。最差性能最优算法[8]则通过引入不确定集，解决导向矢量失配造成的波束质量下降问题，虽然该方法能够根据预先设置的不确定集给出具体的加载量，但是该方法与一般的对角加载方法相同，在提高算法稳健性时容易造成零陷变浅，抗干扰能力降低，而且算法形成零陷较窄，不能抵抗快速移动干扰。本节针对传统的均匀对角加载算法所存在的问题，利用基于非均匀广义对角加载的波束形成算法，通过设计广义对角加载矩阵实现目标信号和干扰信号的非均匀加载，在提高算法稳健性的同时加深并展宽了零陷，从而提高MIMO雷达系统整体性能。假设期望信号来波方向为

(19)

干扰信号来波方向为

(21)

对估计信号协方差矩阵进行特征值分解

(23)

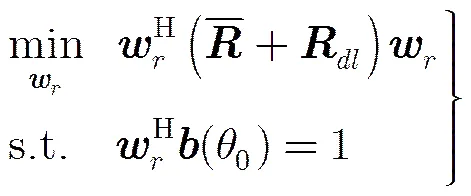
求得接收端加权向量为

(25)

根据式(5)MIMO雷达虚拟阵列结构可知，MIMO雷达联合收发等效加权向量为，通过对MIMO雷达收发方向图设计，实现了MIMO雷达联合方向图的优化，从而提高系统整体性能。由式(16)可知，发射端加权矩阵优化问题为凸优化，可利用凸优化求解程序CVX快速求得，且优化矩阵，因此发射端波形优化复杂度小于。而在接收端波束形成过程中计算复杂度主要集中在式(23)和式(25)，式(23)的计算复杂度为,为积分抽样点数且，式(25)中矩阵逆运算的计算复杂度为，因此接收端稳健波束形成总的计算复杂度为。

5 试验仿真与性能分析

实验1 干扰条件下MIMO雷达发射方向图

图1，图2分别为3种不同方法在干扰条件下的MIMO雷达发射方向图，以及为分析不同发射方向图对接收信号的影响，在MIMO雷达接收端利用非自适应接收器输出信号SINR随输入信号SNR的变化情况。

针对雷达实际应用中可能存在的有源干扰，在干扰方向先验已知的情况下，通过利用MIMO雷达发射方向图设计可以在干扰方向形成具有一定宽度的零陷如图1，确保敌方干扰源始终处于零陷范围之内，从而避免信号被截获。由图2结果分析可知，由于一般的MIMO雷达每个阵元发射全向正交信号，发射信号能量在空间均匀分布，对应于虚拟阵列每个阵元信噪比增益为，造成发射信号能量的浪费，而且在一定程度上提高了杂波信号强度；而DPSS方法和本文方法则通过每个阵元发射部分相关的信号，将信号能量集中在目标空域，虚拟阵列每个阵元信噪比增益为，其中为发射阵列发射增益。通过将发射能量集中，不仅提高了期望目标反射信号强度，同时也抑制了旁瓣区域内杂波信号，进一步提高MIMO雷达输出信号信干噪比。而且相比于DPSS方法，利用最小积分旁瓣方法得到的MIMO雷达发射方向图不仅具有较低的旁瓣，而且可以灵活调整零陷宽度，接收端输出信号SINR更高，而且可以较好地解决己方雷达信号被截获的风险，因此更适用于复杂的电磁环境中。

实验2 干扰条件下MIMO雷达接收方向图

针对雷达在实际战场环境中可能面临的快速移动干扰，以及在接收端存在的信号方向误差等问题，利用基于广义对角加载方法的稳健接收波束形成算法进行仿真分析，并与现有的在实际工程中应用最为广泛的一般对角加载算法[15]和最差性能最优算法[8]进行对比，验证了算法在抑制快速机动有源干扰的有效性及稳健性。设期望信号来波方向为，干扰信号来波方向为，信号方向波动参数，假设期望信号角度误差范围为，期望信号信噪比和干扰信号干噪比分别为10 dB和50 dB，一般对角加载算法加载因子选取为噪声功率的10倍，最差性能最优算法导向矢量不确定集，数据结果为100次蒙特卡罗试验均值。

由图3可以直观看出，本文所提算法相比于其他两种算法不仅加深展宽了零陷，而且旁瓣峰值得到降低。当期望信号来波方向估计存在误差时，由于采用非均匀对角加载，在信号方向加载量，加载后数据输入信号信噪比小于原始信号信噪比，因此算法对期望信号方向失配具有更好的稳健性，在一定误差范围内输出信号的SINR变化较小，如图4所示。当期望信号误差为时，输出信号SINR随输入信号SNR变化情况如图5所示，在期望信号来波方向存在误差时，随着输入信号SNR的提高，一般对角加载算法和最差性能最优算法输出SINR下降，甚至出现信号相消，而对于新算法，在一定误差情况下算法输出SINR仍随着输入SNR的增加而增加，而且不会出现信号相消，因此新的接收波束对期望信号方向失配具有较好的稳健性。

针对接收方向图对快速移动干扰的抗干扰能力，仿真中设干扰信号角度偏移变化范围为，其他参数不变，3种不同算法输出信号SINR随干扰信号角度偏移变化情况如图6所示。对于其他两种算法，当干扰信号角度发生偏移时，干扰移出零陷，造成信号输出信干噪比急剧下降。而对于本文所提新算法，当干扰信号偏移角度小于预先设置的信号方向波动参数时，偏移的干扰信号仍然在零陷之内，输出SINR没有任何变化，但是随着干扰偏移角度的逐渐增大，当偏移角度大于时，干扰信号移出零陷，进而导致输出信号SINR下降。

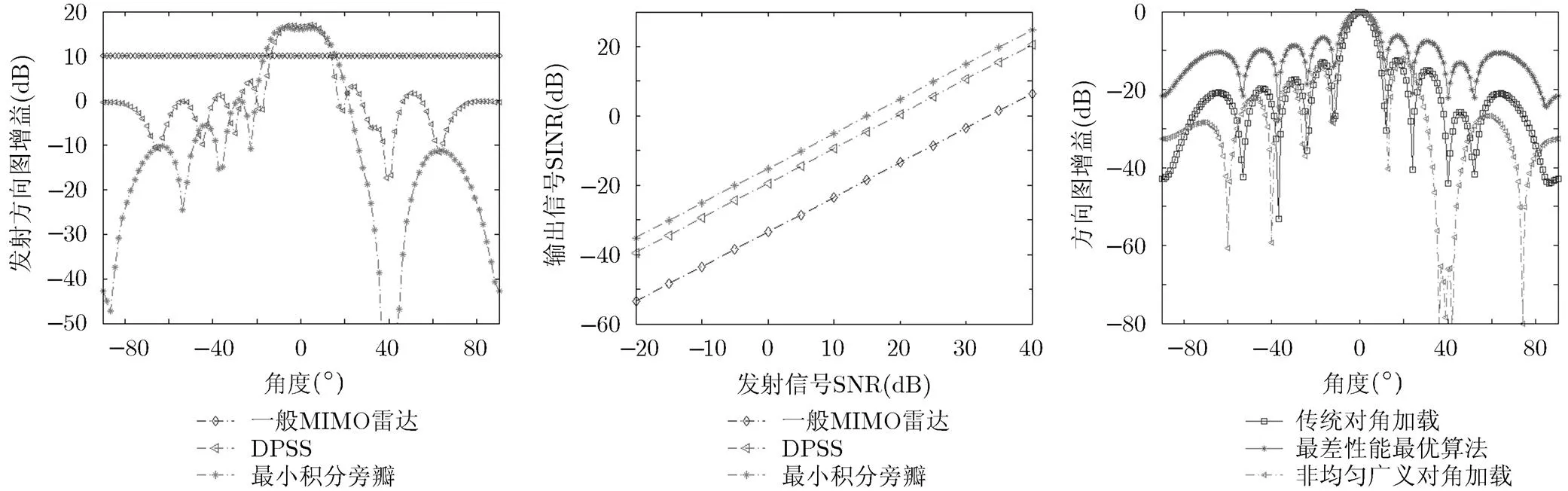
图1 干扰条件下MIMO雷达发射方向图   图2 非自适应接收条件下输出SINR   图3 基于不同算法的接收波束方向图

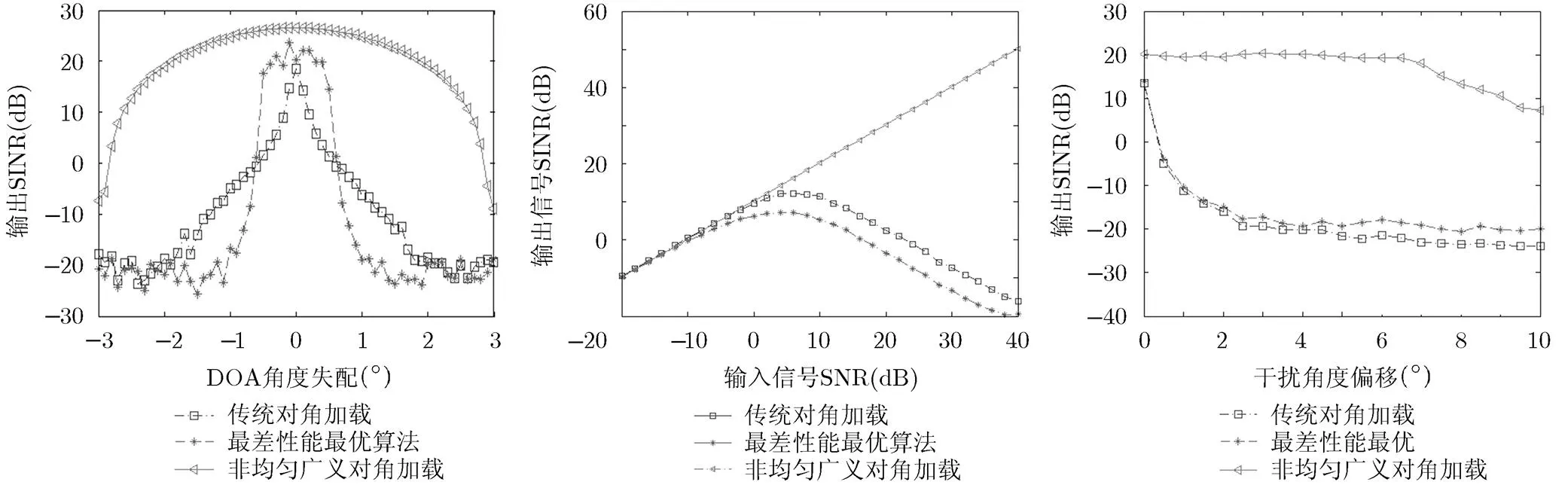
图4 输出SINR随目标信号    图5 期望信号存在误差情况下输出    图6 干扰角度偏移情况下

方向误差变化情况      SINR随输入SNR变化情况              输出SINR

实验3 干扰条件下MIMO雷达收发联合方向图 为更为直观分析对比本文设计的联合收发方向图对MIMO雷达整体性能的改善，仿真分析了不同发射和接收方法的MIMO联合收发方向图。如图7所示，3种不同的发射接收联合方向图，即(1)一般传统MIMO雷达在发射端发射全向正交信号，接收端采用最差性能最优的接收波束形成方法；(2)发射端采用DPSS发射方向图设计方法，接收端采用基于对角加载的接收波束形成方法；(3)发射端采用本文设计的最小积分旁瓣发射图设计方法，接收端采用基于非均匀广义对角加载的稳健波束形成方法。由方向图仿真结果可知，通过同时优化MIMO雷达收发方向图，不仅可以将发射信号能量聚集在目标空域，增强目标反射信号强度并降低杂波噪声，而且可以降低信号被截获概率，提高雷达战场生存能力；同时通过接收端稳健的接收波束，降低实际应用中存在的各种误差和干扰对系统性能的影响。图8显示了MIMO雷达不同收发联合方向图设计方法下，输出信号的SINR。

6 结束语

为提高MIMO雷达在复杂电磁环境下目标跟踪性能，本文针对MIMO雷达收发方向图进行了联合优化设计。在发射端，通过优化发射波束矩阵实现方向图与波形设计的分离，根据最小积分旁瓣准则，以基带信号发射导向矢量与期望导向矢量匹配为约束，在干扰方向信息先验已知的情况下，通过优化发射方向图实现发射能量在目标空域的聚焦，同时降低旁瓣并针对干扰方向形成一定宽度的零陷。在接收端，针对MIMO雷达信号接收所存在的期望信号方向误差以及干扰源快速移动的特性，通过利用非均匀广义对角加载稳健波束形成算法，提高信号接收的稳健性，并通过展宽零陷提高了MIMO雷达信号接收的抗干扰能力。通过实验仿真分析并验证了联合优化MIMO雷达发射和接收方向图方法的有效性。

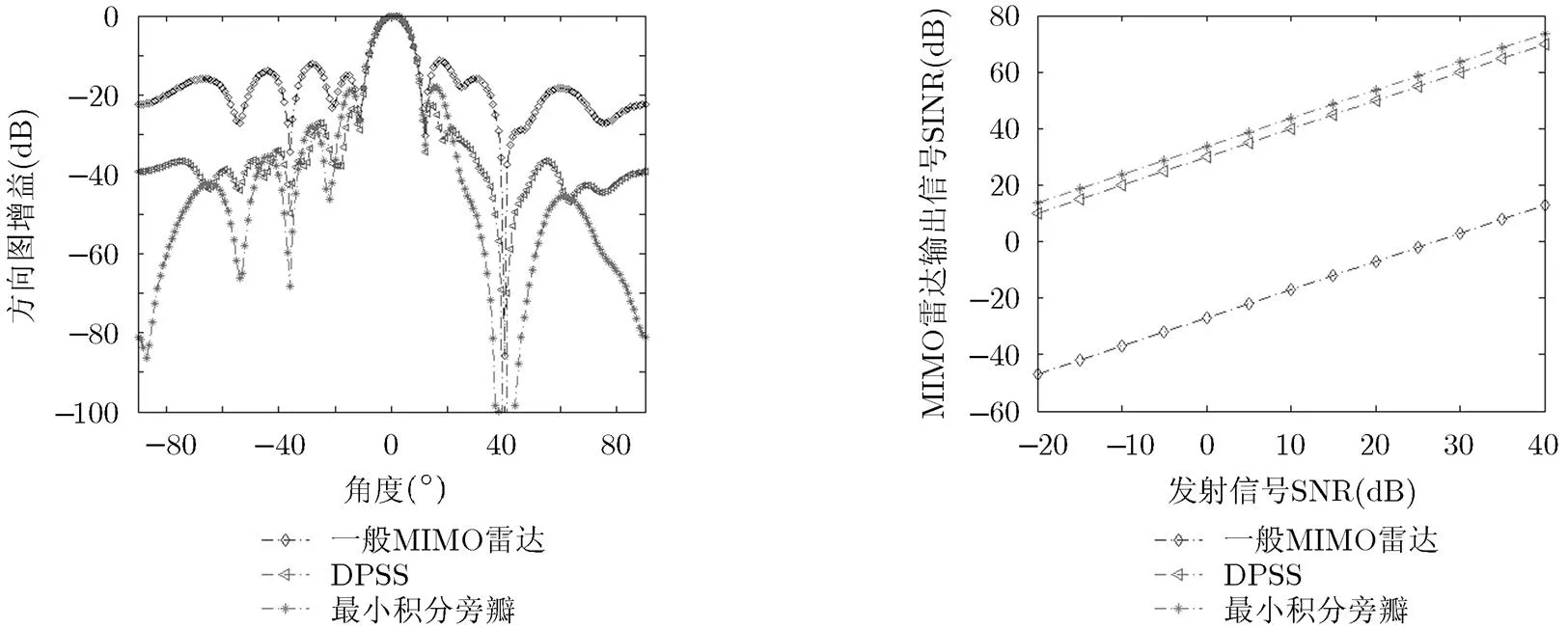
图7 MIMO雷达联合收发方向图   图8 联合收发方向图输出信号SINR随输入SNR变化

参考文献

[1] STOCIA P, LI J, and XIE Yao. On probing signal design for MIMO radar[J]., 2007, 55(8): 4151-4161. doi: 10.1109/TSP.2007.894398.

[2] FUHRMANN D R and ANTONIO G S. Transmit beamforming for MIMO radar systems using signal cross- correlation[J]., 2008, 44(1): 171-186. doi: 10.1109/TAES. 2008.4516997.

[3] GONG P, SHAO Z, TU G,. Transmit beampattern design based on convex optimization for MIMO radar systems[J]., 2014, 94: 195-201. doi: 10. 1016/j.sigpro.2013.06.021.

[4] HASSANIEN A and VOROBYOV S A. Transmit energy focusing for DOA estimation in MIMO radar with colocated antennas[J]., 2011, 59(6): 2669-2682. doi: 10.1109/TSP.2011.2125960.

[5] Khabbazibasmenj A, Hassanien A, Vorobyov S,. Efficient transmit beamspace design for search-free based DOA estimation in MIMO radar[J]., 2014, 62(6): 1490-1500. doi: 10.1109/ TSP.2014.2299513.

[6] BENJAMIN F. On transmit beamforming for mimo radar[J]., 2012, 48(4): 3376-3388. doi: 10.1109/TAES.2012.6324717.

[7] XIANG C, FENG D, and LÜ H. Robust adaptive beamforming for MIMO radar[J]., 2010, 90(12): 3185-3196. doi: 10.1016/j.sigpro.2010.05.022.

[8] LI J, STOCIA P, and WANG Z. On robust capon beamforming and diagonal loading[J]., 2003, 51(7): 1702-1715. doi: 10.1109/TSP. 2003.812831.

[9] LI Y, Vorobyov S, and Hassanien A. Robust beamforming for jammers suppression in MIMO radar[C]. IEEE Radar Conference, Cincinnati, OH, USA, 2014: 629-634.

[10] AHMED S and ALOUINI M S. MIMO radar transmit beampattern design without synthesising the covariance matrix[J]., 2014, 62(9): 2278-2289. doi: 10.1109/TSP.2014.2310435.

[11] CHEN C and VAIDYANATHAN P P. MIMO radar waveform optimization with prior information of the extended target and clutter[J]., 2009, 57(9): 3533-3544. doi: 10.1109/TSP.2009. 2021632.

[12] LIU J, LI H, and HIMED B. Joint optimization of transmit and receive beamforming in active arrays[J]., 2014, 21(1): 39-42, 2014. doi: 10.1109/LSP. 2013.2289325.

[13] CHEN Z, LI H, CUI G,. Adaptive transmit and receive beamforming for interference mitigation[J]., 2014, 21(2): 235-239. doi: 10.1109/LSP. 2014.2298497.

[14] XU H, BLUM R S, and WANG J. Colocated MIMO radar waveform design for transmit beampattern formation[J]., 2015, 51(2): 1558-1568. doi: 10.1109/TAES.2014.140249.

[15] COX H, ZESKIND R, and OWEN M. Robust adaptive beamforming[J].,, 1987, 35(10): 1365-1376. doi: 10.1109/ TASSP.1987.1165054.

王玉玺： 男，1989年生，博士生，研究方向为MIMO雷达及阵列信号处理.

黄国策： 男，1962年生，教授，博士生导师，主要研究方向为雷达通信一体化等.

李 伟： 男，1978年生，副教授，主要研究方向为新体制雷达.

Joint Transmit and Receive Beampattern Design for MIMO Radar under Jamming

WANG Yuxi HUANG Guoce LI Wei

(,,’710077,)

For the problem of signal interception and fast moving jammers in MIMO radar application, this paper designs a new transmit beampattern through optimizing the transmit beamforming matrix based on the minimization of integrated-sidelobe. This new transmit beampattern can not only focus the transmit energy on the desired spatial sector but decrease the level of sidelobe as well as form a nulling at the jammer’s direction with the prior knowledge. At the receiving, a new robust beamforming method based on non-uniform generalized diagonal loading is proposed, which can strengthen the robustness of receiving beamformer against different errors and broaden the nulling adaptively. Through the optimization of joint transmit and receive beampattern for MIMO radar, the interception of signal and fast moving jamming are addressed, which improve the performance of MIMO radar from both transmitting and receiving. Simulation results and comparisons with existing methods demonstrate the feasibility and effectiveness of the proposed methods.

MIMO radar; Beampattern design; Robust beamforming; Nulling broadening

TN958

A

1009-5896(2016)12-3212-07

10.11999/JEIT160002

2016-01-04；改回日期：2016-07-12；

2016-09-30

王玉玺 WYX10013@163.com

国家自然科学基金(61302153)

The National Natural Science Foundation of China (61302153)