基于分数阶傅里叶变换的窄带雷达飞机目标回波特征提取方法

杜 兰 史蕙若 李林森 孙永光 胡 靖



基于分数阶傅里叶变换的窄带雷达飞机目标回波特征提取方法

杜 兰*史蕙若 李林森 孙永光 胡 靖

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071) (西安电子科技大学信息感知技术协同创新中心 西安 710071)

该文研究了常规窄带雷达体制下，利用分数阶傅里叶变换扩展特征域，从而解决直升机、螺旋桨飞机和喷气式飞机3类飞机目标回波分类中的特征提取问题。在现代战场中，直升机、螺旋桨飞机和喷气式飞机具有不同的机动性能，并各自承担着重要的任务。因此，实现这3类飞机的分类具有重大的意义。该文针对3类飞机目标分类的传统特征数目少，包含信息量有限，导致分类性能不够好的问题，基于现有的特征提取方法引入分数阶傅里叶变换(Fractional Fourier Transform, FrFT)，在经过FrFT后的分数域提取3类飞机目标回波的分数阶特征，弥补传统特征的不足。并利用线性相关向量机(Relevance Vector Machine, RVM)的特征选择功能对提取的分数阶特征进行特征选择并分类。基于仿真和实测数据的实验结果证明该文提出的分数阶特征的分类性能较传统时域、多普勒域特征有较大提升。

窄带雷达；分数阶傅里叶变换；特征提取；特征选择；目标分类；喷气引擎调制

1 引言

目前在窄带雷达体制下，对于直升机、螺旋桨飞机和喷气式飞机的分类方法已有诸多研究成果，但在特征提取这一部分，除直接利用飞机的运动参数作为分类特征外，通常根据旋转部件的喷气引擎调制(Jet Engine Modulation, JEM)[1,2]特性对目标进行分类。一般来说喷气式飞机的调制周期最大，即谱线间隔最大，螺旋桨飞机次之，而直升机的调制周期最小，因此，现有方法主要通过提取与雷达时域信号的周期或多普勒域调制谱线的谱线间隔相关的特征来实现3类飞机目标的分类。例如文献[3]提出了时域相关性特征，用以描述时域周期特性；文献[4]在多普勒域提取熵特征和中心矩特征，并进行目标分类和辨识。这些现有特征虽然能在一定程度上体现目标回波的调制特性，但仅对回波的时域谱和多普勒谱进行了分析，特征单一，具有局限性。并且当驻留时间较短时，回波包含信息较少，多普勒谱分辨力也会下降；脉冲重复频率较低时，对时域信号采样率低，且会导致回波多普勒谱混叠，这些都会造成时域和多普勒域的特征分类性能下降。因此时域和多普勒域的特征通常对雷达驻留时间和雷达脉冲重复频率的要求较高。但在实际情况中，常规的窄带雷达常常无法保证对驻留时间和重复频率的相应要求。

在信号处理领域，传统的傅里叶变换是一种应用广泛的数学工具，若将其看作从时间轴逆时针旋转到频率轴的一种线性算子，则分数阶傅里叶变换(Fractional Fourier Transform, FrFT)算子就是可旋转任意角度的算子，可认为是一种广义的傅里叶变换[5]。从本质上讲，信号在分数域上的表示，同时融合了信号在时域和频域的信息，因此FrFT被认为是一种重要的时频分析方法。近年来其理论得到了快速发展，且被广泛应用在时频滤波、多路传输、图像处理等领域。文献[9]详细介绍了FrFT的原理以及目前对FrFT研究的发展和应用现状；文献[10]基于FrFT进行动目标检测；文献[11]利用FrFT进行人脸面部表情识别的研究。

本文提出将分数阶傅里叶变换理论应用到特征提取中，将现有的时域多普勒域特征扩展到分数域，通过分数阶阶次的变换，提取更多的特征，并在此基础上进行特征选择，得到最优的特征组合。基于仿真数据和实测数据的实验结果表明，使用本文提出的基于分数阶傅里叶变换的特征提取方法所提出的特征比传统特征具有更好的可分性，并在低重复频率和短驻留时间的情况下仍能体现出其优势。

2 分数阶傅里叶变换相关理论

在信号处理领域，传统的傅里叶变换是一个研究最为成熟、应用最广泛的数学工具。但傅里叶变换仅能将信号从时域变换到频域，获得信号的整体频谱，而随着信息科学的发展，傅里叶变换对信号分析的局限性也愈发突出。针对这一问题，人们提出并发展了一系列新的信号分析理论与方法，分数阶傅里叶变换作为其中一种在近年来受到广泛关注，它在保留传统傅里叶变换的性质和特点的基础上又添加了其特有的优势，融合了信号在时域与频域的信息。分数阶傅里叶变换可以看成是将信号在时间轴轴上逆时针旋转角度到轴上的射线表示。如图1所示，明显可以看出，当旋转角度时，轴就变成了传统意义上的频率轴轴；若，则为时间轴轴，因此可认为分数阶傅里叶变换是一种广义的傅里叶变换。

图1 平面旋转角到平面

然而在数字信号处理的应用中，必须采用离散形式的分数阶傅里叶变换。近年来，国内外学者提出了多种离散分数阶傅里叶变换(Discrete Fractional Fourier Transform, DFrFT)的定义及快速算法，本文使用的是由文献[12]提出的一种分解方法。这种算法将FrFT分解为信号的卷积形式，从而利用傅里叶变换来计算FrFT。改写式(1)如下：

(3)

将式(3)代入式(2)，即可变换得到FrFT的离散表达形式。根据文献[11]可知，利用原函数的离散样本值可以求出FrFT的离散样本值如式(4)：

3 基于分数阶傅里叶变换的特征提取

目前在窄带雷达体制下，对直升机、螺旋桨飞机和喷气式飞机的分类主要基于3类飞机JEM特性的差异，相关的文献大多在时域和多普勒域进行特征提取[3,4]。其中时域相关性特征峰值函数方差和峰值函数熵反映了信号的时域周期，多普勒域幅值熵在一定程度上反映了谱线的数目，多普勒域幅值方差反映了多普勒域信号的幅度起伏情况，多普勒域中心矩，在一定程度上反映了多普勒域回波的谱宽。

这些传统特征虽也具有较好的分类性能，但其仅从回波的时域谱和多普勒域谱进行分析，特征数目少，包含信息量不足，且对雷达驻留时间和雷达脉冲重复频率的要求较高。因此，针对传统特征的缺点，本文将分数阶傅里叶变换引入到特征提取中，利用分数阶傅里叶变换能将信号变换到时域与频域的中间地带，即分数域的特点扩展特征域，扩充回波信息，以寻求得到更多可以实现3类飞机目标分类的较好特征。

具体特征提取步骤如下：

(1)分数阶信号幅值相关函数域特征：峰值函数方差，峰值函数熵。

(7)

(2)分数阶信号域特征：幅值熵，幅值方差，二阶中心矩，四阶中心距。

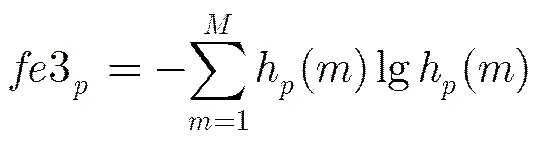
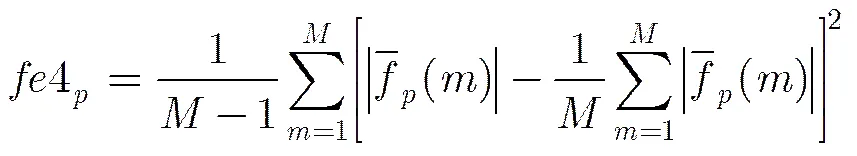
(11)

中心矩是一种简单的平移不变特征，它反映了目标的形状信息。当时为传统多普勒域中心矩，能在一定程度上反映多普勒域回波的谱宽。

4 特征选择及分类

本文在分数域提取特征极大地增多了特征数目，但其中也可能包含一些冗余特征。因此在此基础上需要进行特征选择，不仅可以降低运算量，而且能够提高对3类飞机目标的分类性能。

目前国内外现有的大部分特征选择算法中，最优特征组合的构成大都是用每次从现存特征中增加或者去掉某些特征的方法，直至特征数等于设定的特征数目为止。这种方法不仅在特征数目的设置上有一定困难，而且特征选择和分类的准则也可能存在不一致的问题，造成分类效果的不够理想。因此，本文使用线性相关向量机(Relevance Vector Machine, RVM)[13]来进行特征选择和分类，不仅可以自动确定特征数目，而且通过特征选择和分类器设计的联合优化，解决了特征选择和分类准则不一致的问题。

RVM是在贝叶斯框架下提出的一种有监督的机器学习方法。给定观测数据和对应的目标标号，在监督学习的过程中，我们希望使用这些观测数据和相关的先验信息，找出和之间的映射关系，实现分类器的训练，其中,为样本个数，为类别数目。

多类线性RVM分类器的基本模型为

(13)

5 实验结果

本文分别用仿真数据和实测数据进行训练和测试，用线性RVM分类器进行特征选择并对3类飞机目标分类，之后对比选出特征与传统时域多普勒域特征的分类性能。

5.1 基于仿真数据的实验

仿真数据：仿真按照文献[14-16]产生典型场景下22架飞机的旋转部件回波。

表1 所有分数域特征

0~1阶分数阶特征(共66维) 峰值函数方差特征 峰值函数熵特征 幅值熵特征 幅值方差特征 二阶中心矩特征 四阶中心矩特征

表2比较了本文提出的分数域特征和传统时域特征、多普勒域特征使用线性RVM的分类正确率。从表2可以看出，对于仿真数据，在相同条件下，本文提出的分数域特征在高维情况下能够更好地描述目标特性，比传统的时域或多普勒域特征分类正确率平均高近10个百分点，较大地提高了对3类飞机目标分类的正确率。

表2 在重复频率驻留时间下的仿真实验结果

所用特征分类正确率(%) 时域2维特征()88.00 多普勒域4维特征()80.89 时域多普勒域6维特征 ()91.78 分数域特征97.33

图2给出了仿真数据经线性RVM分类器特征选择的结果。图2中权值较大特征有：,,,,,,,。其中既有传统的时域和多普勒域特征，也包含其它阶次的分数域特征，体现了特征的多元化，可见引入分数域特征的确能起到扩展特征域的作用。

图3和图4分别给出了不同脉冲重复频率下，不同驻留时间对3类飞机分类正确率的影响以及不同驻留时间下，脉冲重复频率对3类飞机分类正确率的影响。

图2 仿真数据用线性RVM分类器特征选择的结果

从图3，图4可以看出在不同的雷达脉冲重复频率和驻留时间下，分数域特征对3类飞机目标的分类正确率普遍高于时域、多普勒域特征，尤其当脉冲重复频率或驻留时间较低的情况下，时域、多普勒域特征的分类性能明显下降，而与之相比，分数域特征则较为稳定。从图5可以看出分数域特征在信噪比为及以上时，分类正确率均高于90%，且在不同信噪比下性能均高于时域、多普勒域特征。

5.2 基于实测数据的实验

实测数据参数：雷达目标包括多种型号的3类飞机，雷达载频为，脉冲重复频率为，信噪比约为。

训练数据：直升机全部选用实测数据，共450个样本；螺旋桨选用部分仿真数据(420个样本)，部分实测数据(30个样本)，共450个样本；喷气式选用部分仿真数据(420个样本)，部分实测数据(30个样本)，共450个样本。

测试数据：全部选用与训练数据不同的实测数据，3类飞机各150个样本。

实验所用的具体特征如表1所示。表3比较了本文提出的分数域特征和传统时域特征、多普勒域特征使用线性RVM的分类正确率。从表3可以看出，对于该组实测数据，使用本文提出的分数域特征，能够显著提高对3类飞机目标的分类正确率，比传统的时域或多普勒域特征分类结果均提高约30个百分点。

表3 在重复频率驻留时间下实测数据实验结果

所用特征分类正确率(%) 时域2维特征()45.33 多普勒域4维特征()51.78 时域多普勒域6维特征()74.22 分数域特征80.22

图6给出了实测数据经线性RVM分类器特征选择的结果。图6中权值较大特征有：,,,,,,,,。

为了分析驻留时间和脉冲重复频率以及噪声对实测数据分类性能的影响，我们对该组实测数据也分别调整了重复频率、驻留时间和信噪比进行分类实验。图7(a)和图7(b)分别给出了脉冲重复频率为和时，3类飞机的平均分类正确率随驻留时间的变化曲线结果。

图3 不同重复频率下，驻留时间与分类正确率之间的关系

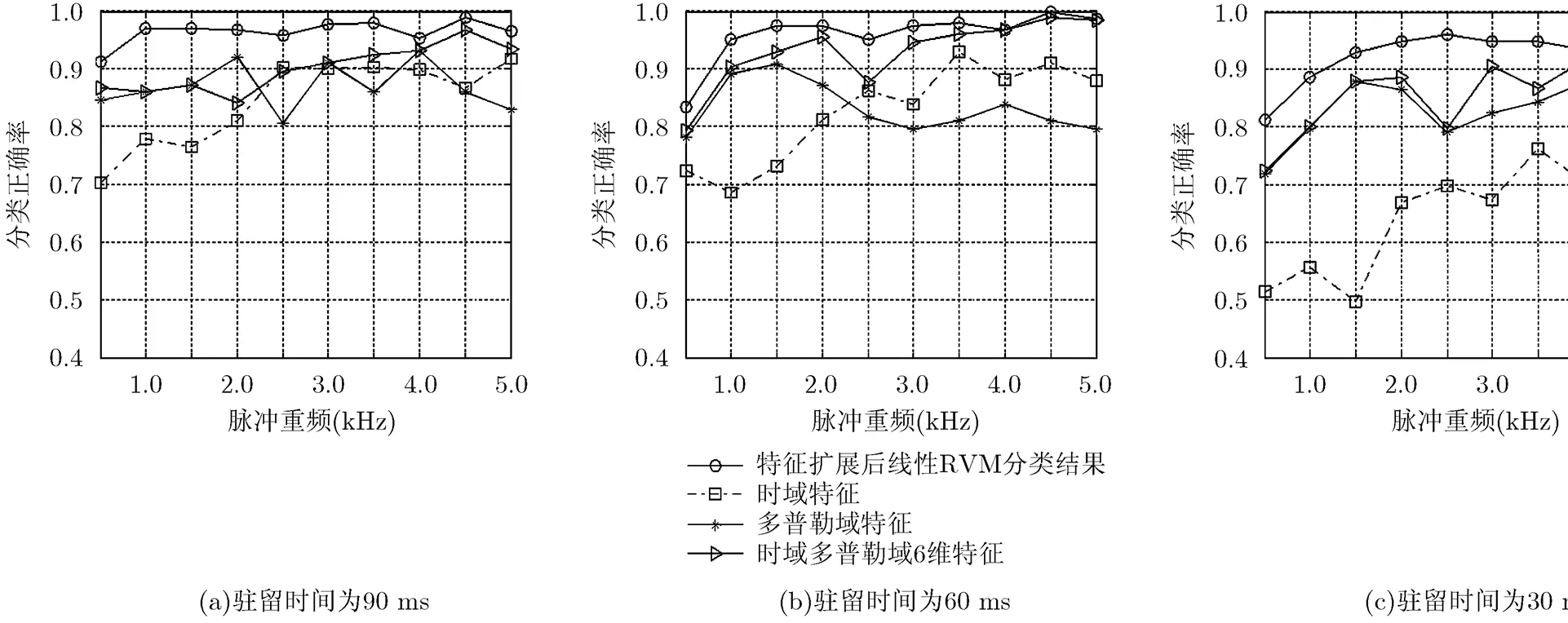
图4 不同驻留时间下，重复频率与分类正确率之间的关系

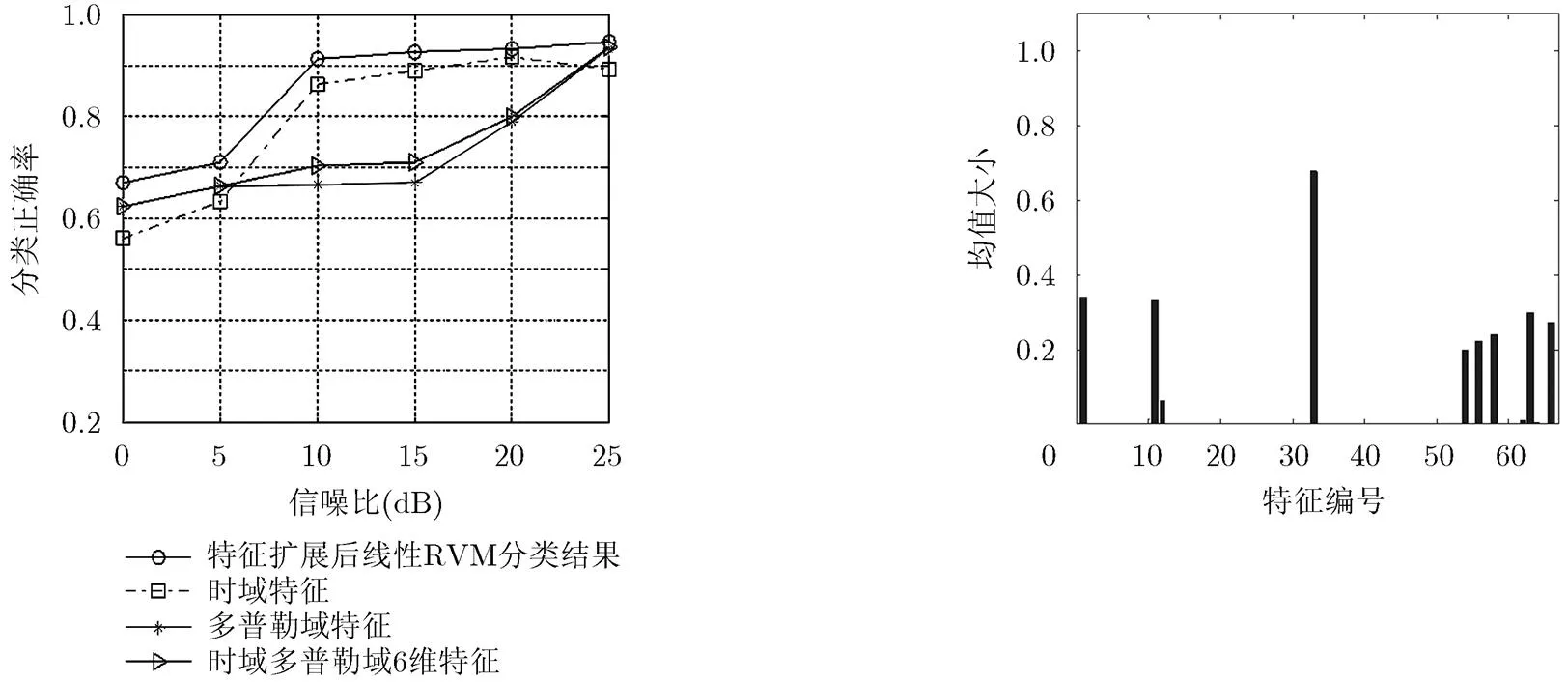
图5 信噪比与分类正确率之间的关系      图6 实测数据用线性RVM分类器特征选择的结果

图7 实测数据驻留时间与分类正确率之间的关系

6 结论

本文提出了基于分数阶傅里叶变换的特征提取方法，该方法使用分数阶傅里叶变换将信号从时域变换到分数域，提取分数域特征，与传统方法相比极大地扩展了特征域，也使信号包含的信息量显著增多，最终使得对3类飞机目标的分类性能得到了较大的提升。实验证明了本文提出的特征提取方法在低重复频率、短驻留时间以及较低信噪比的条件下也具有较好的分类性能。

参考文献

[1] CHEN V C. Radar signatures of rotor blades[J]., 2001, 4391(1): 63-70. doi: 10.1117/12.421231.

[2] YONG Y W, HOON P J, WOO B J,Automatic feature extraction from jet engine modulation signals based on an image processing method[J].,&, 2015, 9(7): 783-789. doi: 10.1049/iet-rsn.2014. 0281.

[3] 杜兰, 李林森, 李玮璐, 等. 基于时域回波相关性特征的飞机目标分类方[J]. 雷达学报, 2015, 4(6): 621-629. doi: 10.12000 /JR15117.

DU Lan,LI Linsen, LI Weilu,Aircraft target classification based on correlation features from time domain echoes[J].,2015, 4(6): 621-629. doi: 10. 12000/JR15117.

[4] 陈娟. 基于多特征融合的雷达目标识别[D]. [硕士论文], 西安电子科技大学, 2010.

CHEN Juan.Radar target recognition based on multi- features fusion[D]. [Master dissertation], Xidian University, 2010.

[5] 陶然, 齐林, 王越. 分数阶Fourier变换的原理与应用[M]. 北京: 清华大学出版社, 2004: 3-4, 31-45.

TAO Ran, QI Lin, and WANG Yue. Principle and Application of Fractional Fourier Transform[M]. Beijing: Tsinghua University Press, 2004: 3-4, 31-45.

[6] OZAKTAS H M and BARSHAN B. Convolution, filtering, and multiplexing in fractional Fourier domains and their relation to LFM and wavelet transforms[J].-, 1993, 11(2): 547-559. doi: 10.1364/JOSAA.11. 000547.

[7] PENG Hsiaowei, CHANG Hsuanting, and LIN Chingchou. 2-D linear frequency modulation signal separation using fractional Fourier transform[C]. International Symposium on Computer Consumer and Control, Xi’an, 2016: 755-758. doi: 10.1109/IS3C.2016.193.

[8] LI Y B, ZHANG F, KANG X J,Image encryption based on the iterative fractional Fourier transform and a novel pixel scrambling technique[C]. IET International Radar Conference, Hangzhou,2015: 1-6. doi: 10.1049/cp.2015.1036.

[9] 冉启文. 小波变换与分数阶傅里叶变换理论及应用[M]. 哈尔滨: 哈尔滨工业大学出版社, 2001: 1-7.

RAN Qiwen. Theory and Application of Wavelet Transform and Fractional Fourier Transform[M]. Harbin: Harbin Institute of Technology Press, 2001: 1-7.

[10] GUAN J, CHEN X L, HUANG Y,Adaptive fractional Fourier transform based detection algorithm for moving target in heavy sea clutter[J].,&, 2012, 6(5): 389-401. doi: 10.1049/iet-rsn.2011. 0030.

[11] 王亚星. 基于分数阶傅里叶变换的人脸识别[D]. [硕士论文], 郑州大学, 2015

WANG Yaxing. Human facial expression recognition based on fractional Fourier transform[D]. [Master dissertation], Zhengzhou University, 2015.

[12] OZAKTAS H M, ARIKAN O, KUTAY M A,Digital computation of the fractional Fourier transform[J]., 1996, 44(9): 2141-2150.

[13] 李志鹏, 马田香, 杜兰, 等. 在雷达HRRP识别中多特征融合多类分类器设计[J]. 西安电子科技大学学报, 2013, 40(1): 111-117. doi: 10.3969/j.issn.1001-2400.2013.01.020.

LI Zhipeng, MA Tianxiang, DU Lan,Multi-class classifier design for feature fusion in radar HRRP recognition [J]., 2013, 40(1): 111-117. doi: 10.3969/j.issn.1001-2400.2013.01.020.

[14] 王宝帅, 杜兰, 刘宏伟. 基于经验模态分解的空中飞机目标分类[J]. 电子与信息学报, 2012, 34(9): 2116-2121. doi: 10. 3724/SP.J.1146.2012.00147.

WANG Baoshuai, DU Lan, and LIU Hongwei. Aircraft classification based on empirical mode decomposition[J].&, 2012, 34(9): 2116-2121. doi: 10.3724/SP.J.1146.2012.00147.

[15] MARTIN J and MULGREW B. Analysis of the theoretical radar return signal from aircraft propeller blades[C]. IEEE International Conference Radar, New York, USA, 1990: 569-572.

[16] BELL M R and GRUBBS R A. JEM modeling and measurement for radar target identification[J]., 1993, 29(1): 73-87.doi: 10.1109/7.249114.

杜 兰： 女，1980年生，教授，博士生导师，研究方向为雷达目标识别技术.

史蕙若： 女，1992年生，硕士生，研究方向为雷达目标识别技术.

李林森： 男，1989年生，硕士生，研究方向为雷达目标识别技术.

孙永光： 男，1991年生，硕士生，研究方向为雷达目标识别技术.

胡 靖： 女，1990年生，硕士生，研究方向为雷达目标识别技术.

Feature Extraction Method of Narrow-band Radar Airplane Signatures Based on Fractional Fourier Transform

DU Lan SHI Huiruo LI Linsen SUN Yongguang HU Jing

(,,’710071,) (,,’710071,)

This paper studies on the feature extraction methods for the classification of helicopter, propeller-driven aircraft, and turbojet using a conventional narrow-band radar system. In the modern battlefield, the helicopter, propeller aircraft and jet aircraft with different motor performances each bear an important task. But the classification performance of the traditional features for the three types of aircraft target classification is not good enough, so the Fractional Fourier Transform (FrFT) is introduced. Based on the existing feature extraction method, the fractional order features of three kinds of aircraft targets are extracted from the fractional domain after FrFT to extend feature domain. Then, the effective features are selected from all extracted features and the classification of the three categories via linear Relevance Vector Machine (RVM) is realized. The experiments demonstrate that the proposed fractional features can improve the classification performance in comparison with some existing features from the time-domain and Doppler-frequency domain.

Narrow band radar; Fractional Fourier Transform (FrFT); Feature extraction; Feature selection; Target classification; Jet Engine Modulation (JEM)

TN957.51

A

1009-5896(2016)12-3093-07

10.11999/JEIT161035

2016-10-08；改回日期：2016-12-01；

2016-12-14

杜兰 dulan@mail.xidian.edu.cn

国家自然科学基金(61271024, 61322103)，高等学校博士学科点专项科研基金博士生导师类基金(20130203110013)，陕西省自然科学基础研究计划(2015JZ016)

The National Natural Science Foundation of China (61271024, 61322103), The Foundation for Doctoral Supervisor of China (20130203110013), The Natural Science Foundation of Shaanxi Province (2015JZ016)