基于知识辅助的MIMO雷达波形设计方法

关 键 李秀友 黄 勇 薛永华



基于知识辅助的MIMO雷达波形设计方法

关 键 李秀友*黄 勇 薛永华

(海军航空工程学院信息融合技术研究所 烟台 264001)

该文针对雷达系统受到天线主瓣和副瓣杂波以及强干扰影响时性能下降问题，提出基于距离扩展目标和杂波先验信息的MIMO雷达波形设计方法。首先建立了目标函数，综合考虑了波束主瓣增益、旁瓣杂波抑制能力以及目标输出SCNR的改善性能；然后在优化问题求解中对约束条件进行松弛，使得波形矩阵空域和时域2维解耦合，从而实现空域波束形成和时域波形设计独立优化求解；其次利用L-BFGS算法设计恒模的发射波形矩阵，形成低副瓣的波束方向图和较深的强杂波抑制凹口，并基于目标输出SCNR最大化准则，利用迭代算法分步求解优化的主瓣发射波形和接收滤波器；最后通过电磁仿真的距离扩展目标数据验证所提算法的有效性。

MIMO雷达；知识辅助；波形设计；距离扩展目标

1 引言

近年来，大量文献研究了基于知识辅助的波形设计方法，利用背景和目标的先验信息智能化的调整发射波形，能够提高雷达目标检测性能、跟踪精度和识别概率，因此知识辅助的波形设计技术将全面提高现代雷达系统的整体性能。

文献[8,9]研究了基于国家土地覆盖数据库(NLCD)等辅助知识的波形设计方法，在脉间设计最优编码波形，提高系统对窄带点目标的检测性能。文献[10]研究了基于距离扩展目标和杂波先验信息的波形优化设计算法，提出了交替求解发射波形和接收滤波器的迭代算法，并具有较好的收敛性和SINR改善性能。但是该文献未考虑波束形成问题，所设计的发射波束在目标方向增益较低，无法提高目标输出SNR。

MIMO雷达由于每个阵元可以发射不同的编码波形，因此波形设计中具有较大的自由维度，能够设计优化波形同时在空域和时域2维匹配目标并抑制杂波[11]。当雷达系统工作在复杂场景时，会受到从天线主瓣和副瓣进入的杂波以及来自副瓣强干扰的影响，为了有效抑制杂波和干扰，需要在波束形成中自适应形成深凹口方向图对准干扰方位，在波形设计过程中对杂波进行白化并匹配目标，使得目标输出SCNR最大化。要设计MIMO雷达波形矩阵使得波束方向图和时域波形同时达到最优难度较大[12]。文献[13]在研究MIMO雷达非平稳条件下的波形设计问题时，在优化求解过程中对来自副瓣的微弱杂波做了近似处理，将波束形成问题和波形优化问题解耦合，再分层次分别求解最优发射波束方向图和最优发射波形及接收滤波器。

受以上思路的启发，本文提出了一种基于距离扩展目标和杂波先验信息的MIMO雷达波形设计方法。首先建立了目标函数，综合考虑了波束主瓣增益、旁瓣杂波抑制能力以及目标输出SCNR的改善性能；然后在优化问题求解中对约束条件进行松弛，使得波形矩阵空域和时域2维解耦合，从而实现空域波束形成和时域波形设计独立优化求解；其次利用L-BFGS算法设计恒模的发射波形矩阵，形成低副瓣的波束方向图和较深的强杂波抑制凹口，并基于目标输出SCNR最大化准则迭代分步求解优化的发射波形和接收滤波器；最后通过距离扩展目标的电磁散射仿真数据验证本文算法的有效性。

2 系统模型及优化问题分解

(2)

(4)

(6)

(8)

目标回波信号和杂波回波信号经过接收波束并作归一化处理可得

(10)

(12)

则接收滤波器输出的SCNR可以表示成

(14)

文献[13]在附录中证明，经过发射波束和接收波束的空间调制，主瓣杂波通常远大于副瓣杂波，即。因此，对式(14)可以进行松弛，仅考虑来自主瓣的杂波，对于来自副瓣的强杂波可以通过自适应形成波束方向图深凹口实现旁瓣杂波抑制。为了保证目标所在方位的照射能量，波束主瓣增益应该满足

(16)

经过天线波束方向图调制，来自副瓣的杂波能量为不同方位杂波能量与天线副瓣增益乘积之和，并对副瓣杂波总能量进行约束。

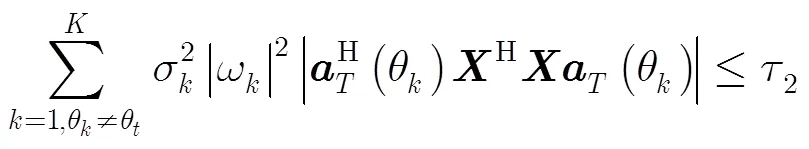
为了简化优化表达式，将约束条件式(16)和约束条件式(17)进行合并，则约束条件为

(18)

则发射波形恒模条件约束下的MIMO雷达发射波形和接收滤波器联合优化设计问题可以表示成如式(19)所示优化问题：

其中，约束条件1用于提高SCNR，约束条件2用于控制波束主瓣增益损失和来自副瓣波束的杂波功率，约束条件3保证发射波形的恒模特性。

当2足够小的时候，来自天线副瓣的杂波足够小，可以近似处理，则式(19)问题可以松弛为

在较小的主瓣损失约束条件下，主波束合成波形幅度起伏相对较小，可以近似认为恒模发射波形，可以近似表示为,，其中为发射波形相位，则发射波形矩阵可以表示成[13]

(21)

(23)

上述问题可以认为是知识辅助的波束形成和波形矩阵设计问题，通过控制波束副瓣来降低来自副瓣的杂波功率，并保证了主瓣波束发射功率。

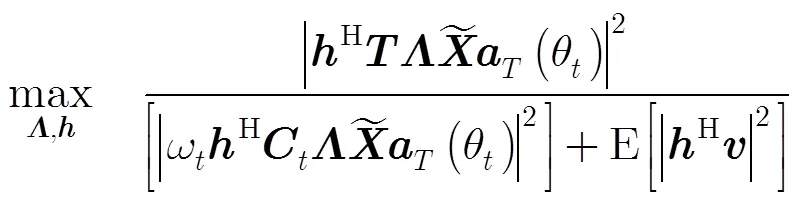
子问题2可以认为是知识辅助的发射波形和接收滤波器联合优化设计问题。

3 知识辅助MIMO雷达分层波形设计

3.1 知识辅助的波束形成和波形矩阵设计

由于优化问题式(24)的目标函数和约束条件都是非凸的，求取该问题的全局最优解难度较大。根据文献[14]中对非凸二次最小化问题的分析，可以看出四阶三角多项式的局部最小值为全局最小值的1/2近似值，即对于如下的四阶三角多项式函数

(27)

则优化问题式(24)可以等价表示成如式(29)所示矩阵形式

(29)

其中，

可以得到

(30a)

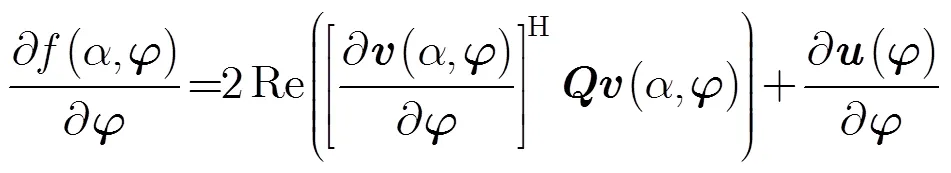
其中，

(31)

无约束优化问题式(24)可以利用拟牛顿法高效求得近似解，并定义相邻两次迭代波形的相对变化量：

3.2 知识辅助的发射波形-接收滤波器联合优化

根据文献[10]的交替迭代算法，问题式(33)可以先假设已知求得最优的接收滤波器，再根据求得的最优接收滤波器求，具体迭代步骤如下，其中步骤1用于初始化，步骤6用于计算相邻两次迭代优化波形对SINR的改善值，当改善值小于给定值时循环终止。具体运算步骤如下：

步骤5 求取发射波形

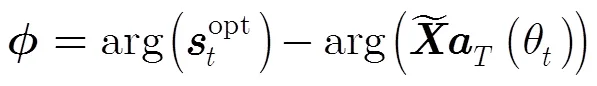
从而最优发射波形矩阵可以表示为

(35)

3.3 运算量分析

在上述算法中，需要利用迭代算法设计MIMO雷达的2维发射波形矩阵和接收滤波器，其中矩阵求导和求逆运算均会消耗大量的运算量，因此，需要对上述两个子问题求解过程的运算量进行分析。子问题1迭代算法中的步骤1存在矩阵求导，对应的式(30)需要次复乘运算，其他步骤运算量为，因此，当迭代次数为次时，子问题1求解过程的运算量为。子问题2迭代算法中主要运算量消耗在步骤3和步骤5的矩阵求逆运算中，步骤3中矩阵维数为，求逆运算的运算量为，其中；步骤5中矩阵维数为N，求逆运算的运算量为，因此，当迭代次数为次时，子问题2迭代运算的运算量为。

4 仿真结果及性能分析

4.1 仿真条件及数据说明

实验过程中目标采用了波音727飞机电磁散射仿真数据，其中雷达为X波段步进频体制，中心工作频率为9 GHz，系统带宽为150 MHz，脉冲重复频率为20 kHz，回波脉冲数为256，距离单元个数64，目标为距离扩展目标占据多个距离单元。仿真的目标回波数据原本用于ISAR成像算法验证，由于目标存在转动现象，不同脉冲对应不同的视角，图1为目标一个视角的1维距离像。仿真过程中，令扩展目标回波信号所在方位角，目标脉冲响应为。

4.2 知识辅助的波束形成

图4给出了根据本文算法所设计的优化发射波束方向图，从图中可以看出，波束旁瓣功率水平比主波束低约20 dB，并在和两个强杂波方位形成深凹口，凹口深度接近，能够有效地抑制来自波束旁瓣的强杂波干扰，相对于未优化波束方向图，基于本文优化方法设计的波束获得了更低的副瓣和更深的杂波抑制凹口。

4.3 知识辅助的发射和接收波形优化设计

图1 波音727飞机距离扩展目标1维距离像  图2 杂波方位和距离2维响应    图3 不同方位的杂波功率水平(dB)

图6给出了目标256个不同视角回波的输出SCNR，仿真过程中每个目标回波的输出SCNR通过1000次不同杂波的平均得到。从图6中可以看出，由于目标视角变化，回波信号存在一定的起伏现象，使得最终输出SCNR存在一定的起伏，但是不同视角回波输出SCNR围绕均值起伏范围不超过3 dB，这说明在已知目标脉冲响应和杂波脉冲响应先验知识的条件下，本文算法均能够保证较大的SCNR改善性能，且具有较好的稳健性。

5 结束语

本文为了抑制来自天线主瓣和副瓣杂波以及强干扰，提出了一种基于距离扩展目标和杂波先验信息的MIMO雷达波形设计方法。该方法综合考虑了波束主瓣增益、旁瓣杂波抑制能力以及目标输出SCNR的改善性能，在优化问题求解过程中对约束条件进行松弛，使得空域最优波束形成和时域优化波形设计独立求解，并利用L-BFGS算法和分步迭代算法求解恒模的发射波形矩阵，最后通过电磁仿真的距离扩展目标验证所提算法。基于目标和杂波先验知识的优化波形能够通过空域和时域2维抑制杂波并匹配距离扩展目标，能够大幅提高输出SCNR，具有较大的应用价值。但是先验知识数据库如何获取、如何进行交互等问题还有待进一步深入研究。

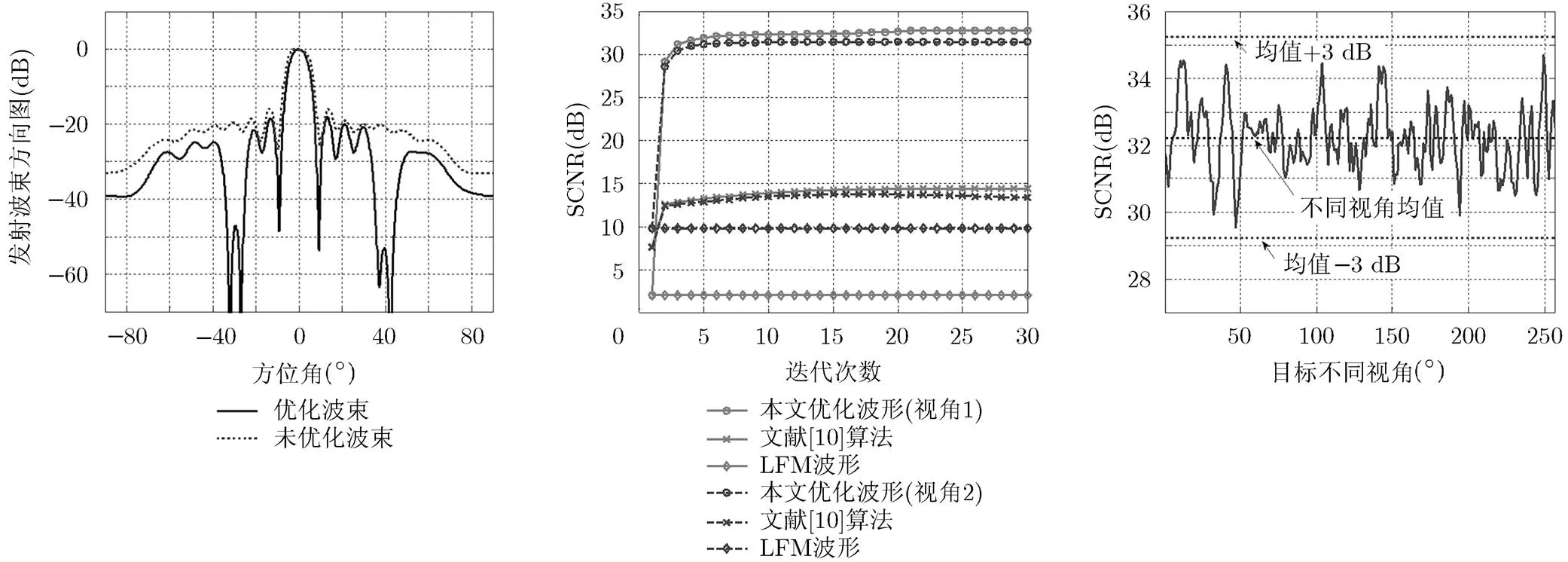
图4 优化后的发射波束方向图  图5 目标两个视角输出SCNR与迭代次数关系图  图6 目标不同视角的SCNR输出图

参考文献

[1] VESPE M, JONES G, and BAKER C J. Lessons for radar: waveform diversity in echolocating mammals[J]., 2009, 26(1): 65-75.

[2] YANG Y and BLUM R S. Minimax robust MIMO radar waveform design[J]., 2007, 1(1): 147-155.

[3] COCHRAN D, SUVOROVA S, HOWARD S D,Waveform libraries: measures of effectiveness for radar scheduling[J]., 2009, 26(1): 12-21.

[4] JIU Bo, LIU Hongwei, ZHANG Lei,Wideband cognitive radar waveform optimization for joint target radar signature estimation and target detection[J]., 2015, 51(2): 1530-1546.

[5] YAN Junkun, JIU Bo, LIU Hongwei,Prior knowledge- based simultaneous multibeam power allocation algorithm for cognitive multiple targets tracking in clutter[J]., 2015, 63(2): 512-527.

[6] YAN Junkun, LIU Hongwei, JIU Bo,Power allocation algorithm for target tracking in unmodulated continuous wave radar network[J]., 2015, 15(2): 1098-1108.

[7] TURLAPATY A and JIN Yuanwei. Bayesian sequential parameter estimation by cognitive radar with multiantenna arrays[J]., 2015, 63(4): 974-987.

[8] AUBRY A, DE MAIO A, FARINA A,. Knowledge- aided (potentially cognitive) transmit signal and receive filter design in signal-dependent clutter[J]., 2013, 49(1): 93-116.

[9] AUBRY A, DE MAIO A, JIANG Bo,. Ambiguity function shaping for cognitive radar via complex quartic optimization[J]., 2013, 61(22): 5603-5619.

[10] CHEN Chunyang and VAIDYANATHAN P P. MIMO radar waveform optimization with prior information of the extended target and clutter[J]., 2009, 57(9): 3533-3544.

[11] GUERCI J R. Cognitive Radar: The Knowledge-Aided Fully Adaptive Approach[M]. Norwood, MA, USA, Artech House, 2010, Chapter 2.

[12] HULEIHEL W, TABRIKIAN J, and SHAVIT R. Optimal adaptive waveform design for cognitive MIMO radar[J]., 2013, 61(20): 5075-5089.

[13] JIU Bo, LIU Hongwei, WANG Xu,.Knowledge-based spatial-temporal hierarchical MIMO radar waveform design method for target detection in heterogeneous clutter zone[J]., 2015, 63(3): 543-554.

[14] KISIALIOU M, LUO X D, and LUO Z Q. Efficient implementation of quasi-maximum-likelihood detection based on semidefinite relaxation[J]., 2009, 57(12): 4811-4822.

[15] WANG Yongchao, WANG Xu, LIU Hongwei,. On the design of constant modulus probing signals for MIMO radar[J]., 2012, 60(8): 4432-4438.

关 键： 男，1968年生，教授，博士生导师，研究方向为雷达目标检测与跟踪、侦察图像处理和信息融合等.

李秀友： 男，1983年生，博士生，研究方向为认知雷达波形设计、海杂波中目标检测等.

黄 勇： 男，1979年生，博士，研究方向为MIMO雷达波形设计及目标检测等.

薛永华： 男，1986年生，博士，研究方向为MIMO雷达波形设计及目标检测等.

Knowledge-aided MIMO Radar Waveform Design Method

GUAN Jian LI Xiuyou HUANG Yong XUE Yonghua

(,,264001,)

In order to solve the problem of performance degradation when radar system is influenced by clutter from mainlobe and sidelobe, MIMO radar waveform design algorithm based on knowledge of range-spread target and clutter is investigated. Firstly, an optimization cost function is established, which includes mainlobe gain, sidelobe clutter suppression capability and Signal to Clutter plus Noise Ratio (SCNR) improvement. Secondly, to tackle the optimization problem, a relaxation is made to decouple spatial and temporal domain of the waveform matrix, beamforming and waveform design can be solved independently. Thirdly, L-BFGS algorithm is used to design the unimodular waveform matrix, beampattern with lower sidelobe and deep null is got. Based on maximization of SCNR, transmitted waveform and receiving filter are designed by iterative algorithm. Finally, the effectiveness of the proposed algorithm is verified by electromagnetic simulation of range-spread target.

MIMO radar; Knowledge-aided; Waveform design; Range-spread target

TN957.51

A

1009-5896(2016)12-3063-07

10.11999/JEIT160008

2016-01-04；改回日期：2016-05-30；

2016-07-19

李秀友 lixiuyou2012@163.com

国家自然科学基金(61471382, 61401495, 61201445, 61179017, 61501487)，山东省自然科学基金(2015ZRA06052)，“泰山学者”建设工程专项经费

The National Natural Science Foundation of China (61471382, 61401495, 61201445, 61179017, 61501487), Natural Science Foundation of Shandong Province (2015ZRA 06052), Special Funds of Taishan Scholars Construction Engineering