一种基于复阻抗的电压暂降定位方法
2016-10-13程志友王雪菲
程志友,王雪菲,徐 佳
一种基于复阻抗的电压暂降定位方法
程志友1,2,王雪菲2,3,徐 佳2
(1.教育部电能质量工程研究中心, 安徽 合肥 230601;2.安徽大学电子信息工程学院, 安徽 合肥 230601;3.安徽四创电子股份有限公司, 安徽 合肥 230088)
电压暂降是目前电力系统最重要的电能质量问题之一,日益受到社会的关注。针对传统算法运算复杂、精度较差的缺陷,提出了一种基于复阻抗的电压暂降定位方法。该方法首先对检测到的电压和电流信号分别进行Hilbert变换构造其解析信号,然后计算对应的复阻抗,利用电压暂降发生时阻抗和相位突变的特性,结合超限判别,准确定位电压暂降的发生时刻,检测出其持续时间,最后通过实验验证所提方法的有效性。实验结果表明,该方法检测精度高、易于判别,具有广泛的推广价值。
Hilbert变换;复阻抗;电压暂降;电能质量
0 引言
随着大功率电力电子和自动控制等技术的迅猛发展,以及各种新型用电设备和冲击性负荷的大量使用,供、用电双方对电能质量提出了越来越高的要求[1]。在电能质量问题的各种现象中,电压暂降已经上升为最重要的电能质量问题之一[2]。电压暂降不仅导致电压敏感设备不能正常工作,而且会带来巨大的经济损失,甚至造成设备毁坏和人员伤亡。引起电压暂降的原因有很多,其中短路故障、大负荷装置启动和雷击是引起电压暂降的最主要原因;在输配电系统中发生开关操作、变压器以及电容器组的投切等事件时,也会引起电压暂降[3]。国内外广大电力工作者对如何改善和治理电压暂降问题,做了广泛的研究[4-10]。而解决这些问题的前提是快速准确地定位电压暂降的发生以及检测其持续时间。Flavio B. Costa等提出了一种基于小波系数能量的电压暂降分析方法[11],该方法由于使用了均方根电压值进行数据分析,导致时间滞后,从而产生了定位误差。文献[12]提出了一种使用强跟踪滤波器检测暂态电能质量扰动的方法,在处理电压暂降问题中能够有效捕捉电压暂降的发生,但需要对大量的数据进行处理,实时性不高。M. Sabarimalai Manikanda等提出了一种使用稀疏信号分解检测和分类电能质量扰动的方法[13],在处理电压暂降问题时,需要同时提取原始信号的细节和近似信号,再对包含细节或近似信号的瞬时均方根波形进行提取分析,运算繁杂,计算量大。
为了克服传统算法运算复杂、检测精度较差的问题,本文基于电压暂降发生时电压下降伴随电流上升导致阻抗大幅跌落的特性,提出了一种结合Hilbert变换的电压暂降定位方法,用于检测线路故障引起的电压暂降。首先对检测到的电力系统电压和电流信号分别进行Hilbert变换,构造其解析式,然后计算出对应的阻抗模值以及相位。在电压暂降发生时,该方法相较于电压幅值的变化,阻抗幅值会相对急剧,结合设定的超限判别,可以准确定位电压暂降的发生以及检测其持续时间。实验表明,阻抗模值会凸显电压暂降的发生,同时由于检测精度高,易于判别,具有较高的应用价值。
1 基于复阻抗的电压暂降定位原理
1.1 Hilbert变换
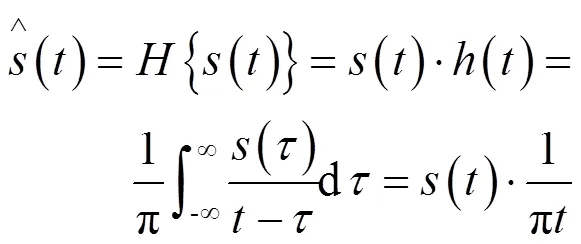
(2)

通过以上分析可以得出,Hilbert变换相当于幅频特性为1,负频率分量+90°相移、正频率分量-90°相移的全通滤波器。信号经过Hilbert变换后,解析信号剔除了实信号的负频率成分,同时不会造成任何信息损失。

其中
(5)
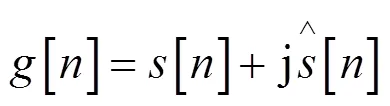
1.2 电压暂降信号检测
复阻抗应用于电能质量扰动信号分析,首先需要定义其抽样信号模型,这里构造电压和电流信号的仿真模型为

式(7)经Hilbert变换以后得到电压、电流信号的解析信号为
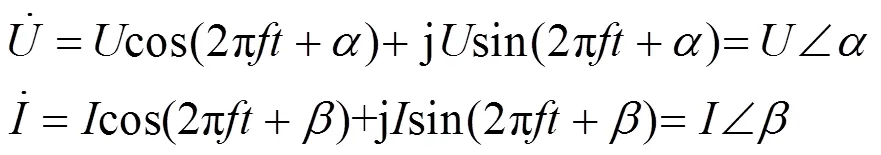
(9)
1.3 电压暂降超限判别
电压暂降是指供电电压均方根值在短时间突然下降的事件,其典型持续时间为0.5~30周波,IEEE将其定义为下降到额定值的90%~10%。而且,电压暂降往往还伴随有电压相位跳变。电压暂降的幅值、持续时间和相位跳变是标称电压暂降的最重要的三个特征量[1]。
离散的电压电流信号分别经过Hilbert变换,构造出相应的解析信号,得到实际复阻抗的模值和相位;同时由软件锁相环获取的额定电压信号和实际电流信号分别经过Hilbert变换,构造相应解析信号后得到复阻抗的额定模值和额定相位。根据式(10)及电压暂降相关定义获取电压暂降的发生时间和持续时间,从而判定电压暂降的发生。其中为实际阻抗和额定阻抗,和分别为实际电压、电流和额定电压构造的相应解析信号。

根据电压暂降的定义,设定实际阻抗下降到额定阻抗的90%~10%之间,即发生电压暂降。通过软件锁相环锁定获取判别基准线,从而划定两条分别为0.9 p.u.和0.1 p.u.的电压暂降判别线。在电压暂降发生的判定中,根据阻抗模值与其判别线的两次相交,判定电压暂降的产生时刻和持续时间。
在电压暂降发生时,电流会随之上升,对应的阻抗模值则会大幅下降,从而更精准地检测到电压暂降的发生;阻抗相位的检测主要用于电压发生暂降时导致相位跳变相关机理的分析。
2 基于复阻抗的电压暂降定位仿真
为了对扰动信号进行分析,下面模拟了电压暂降的信号。首先讨论发生电压暂降时未伴随相位跳变的情况,构造的电压和电流信号模型如式(11)和式(12)所示。

(12)
输入的电压和电流信号波形如图1所示。将上述信号分别进行Hilbert变换,构造其解析信号,从而得到相应的阻抗模值和相位,阻抗模值中的虚线表示电压暂降的两条判别线,如图2所示。
由图2可以看出,在电压暂降发生的0.1~0.2 s,阻抗模值从22 Ω跌落至5 Ω,相位保持在60°不变,仅在0.1 s和0.2 s处有两个小突起,电压暂降持续了0.1 s。
接下来对比发生电压暂降时伴随相位跳变的情况,构造的电压和电流信号模型如式(13)和式(14)所示。

图1 电压波形和电流波形

图2 阻抗模值和相位

(14)
电压和电流信号的波形如图3所示,此时发生电压暂降的同时伴随了相位跳变,电压初相位由2π/3跳变为π/3,电流初相位由π/3跳变为2π/3。将上述信号分别经过Hilbert变换,得到其解析信号,检测出对应的阻抗模值和相位,同样阻抗模值中的虚线表示电压暂降的两条判别线,如图4所示。
由图4可以看出,电压暂降发生在0.1~0.2 s,阻抗模值也从22 Ω跌落至5 Ω,而阻抗相位由60°跳变到了-60°,电压暂降同样持续了0.1 s。在实际应用中,阻抗模值为判定标准,相位用于辅助分析。
基于上述实验效果,下面通过搭建三相电压暂降的模型进行验证,此模型为定步长采样,检测时间在0~0.5 s。设置三相电源相间电压为380 V,频率为50 Hz,内阻为0.312 Ω,电抗量为2.081 82 Ω;线路Line 1、2、3、4均为50 km;三相开关在0.15~0.3 s闭合,A、B、C三相同时作用,开关电阻为0.001 Ω,缓冲电阻为0.000 006 Ω,缓冲电容无穷大。图5、图6和图7分别为仿真模型、三相电压和电流波形。

图3 电压波形和电流波形
可以看到图6中A、B、C三相的电压幅值从311.81 V降至180.78 V,在三相开关作用的0.15 s和0.3 s都发生了短暂的畸变,0.3 s之后A、B、C三相的电压幅值最大时分别达到514.35 V、753.29 V和582.66 V,之后三相电压幅值又很快回到了初始的311.81 V;图7中A、B、C三相的电流幅值初始值为20.98 A,0.15 s三相开关闭合后发生显著增大,最大幅值分别达到49.89 A、42.07 A和44.32 A,之后在0.3 s三相开关断开后又恢复到之前的20.98 A。

图4 阻抗模值和相位
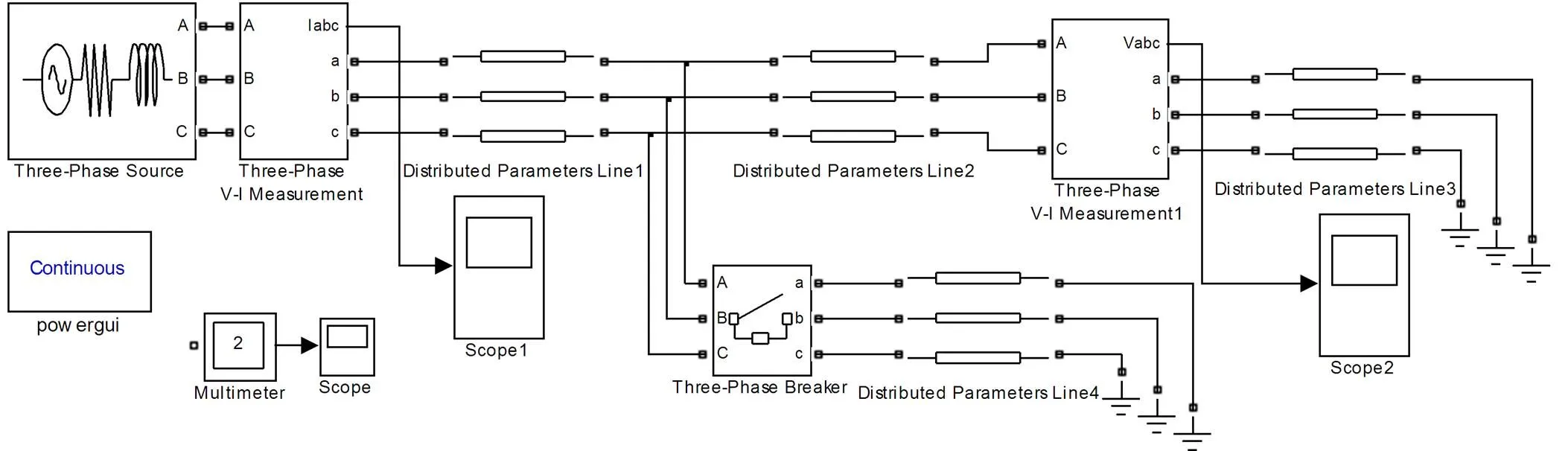
图5 仿真模型
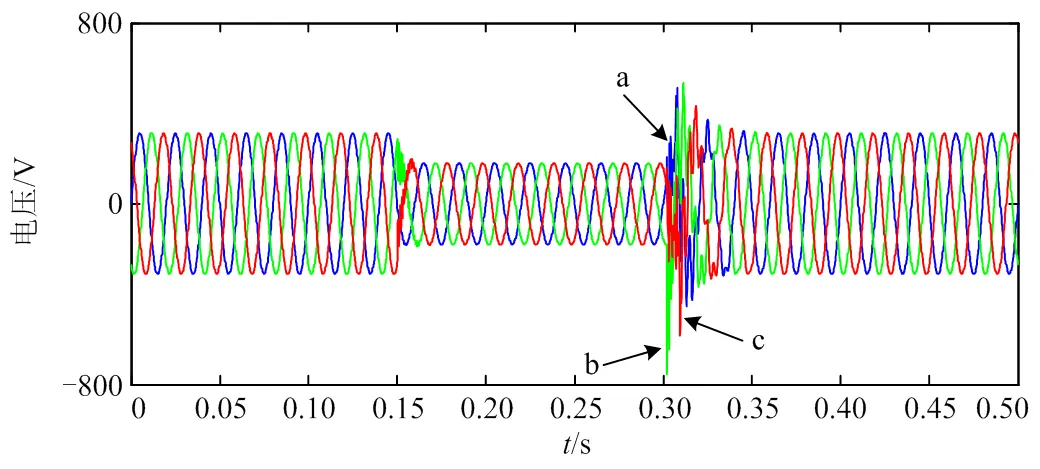
图6 三相电压仿真波形
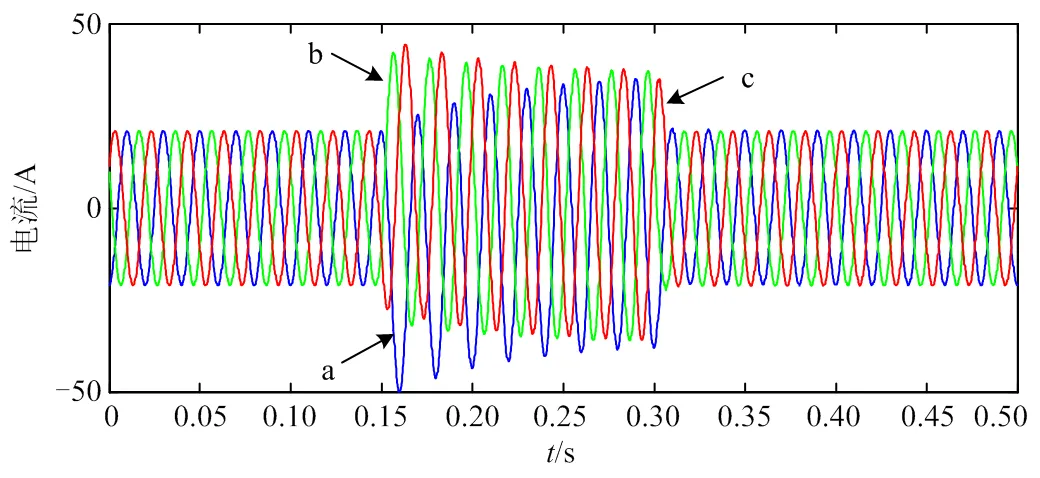
图7 三相电流仿真波形
下面将得到的仿真波形数据提取出来进行分析。对三相中的每一组电压电流数据分别进行Hilbert变换获取其解析信号,从而得到相应的阻抗模值和相位;同时结合软件锁相环获取的电压暂降判别线,检测这三组数据,阻抗模值中的虚线即表示电压暂降的两条判别线,如图8所示。
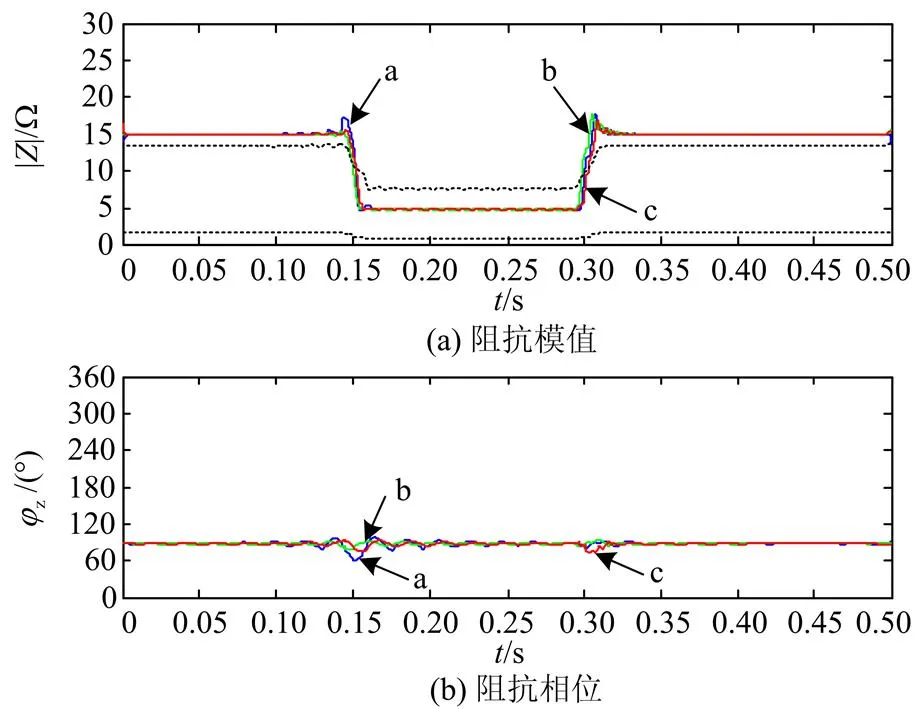
图8 阻抗模值和相位
由图8可以看出,A、B、C三相的阻抗模值与电压暂降判别线分别发生了两次相交,第一次相交分别在0.152 s、0.149 s 和0.152 s,第二次相交分别在0.300 s、0.299 s和0.302 s。这里说明了此次电压暂降发生的时间在0.15~0.3 s之间,持续时间为0.15 s。通过以上阻抗模值和电压暂降判别线的相交可以准确地将电压暂降发生的时间进行定位,表明本文提出的方法具有一定的实用价值。
3 实际数据分析
为了进一步验证该方法的可行性,对某大型企业的电压和电流信号进行监测,提取了某日11时06分38秒感应电动机启动时的电压和电流数据,如图9和图10所示。测得电压、电流信号的初始幅值分别为310.23 V和26.14 A,感应电动机启动平稳后的幅值分别为295.13 V和25.98 A。
如图11所示,对检测到的上述三相电压、电流信号进行处理,可见阻抗模值在感应电动机启动前为11.87 Ω,平稳后为11.36 Ω。A、B、C三相阻抗模值与电压暂降判别线的两次相交时间分别在38.321 s、38.318 s、38.318 s和38.348 s、38.349 s、38.351 s,即电压暂降发生的时间在38.32~38.35 s之间,持续了0.03 s。感应电动机启动前阻抗相位在28.74°,启动平稳后变为42.49°。

图9 电压波形
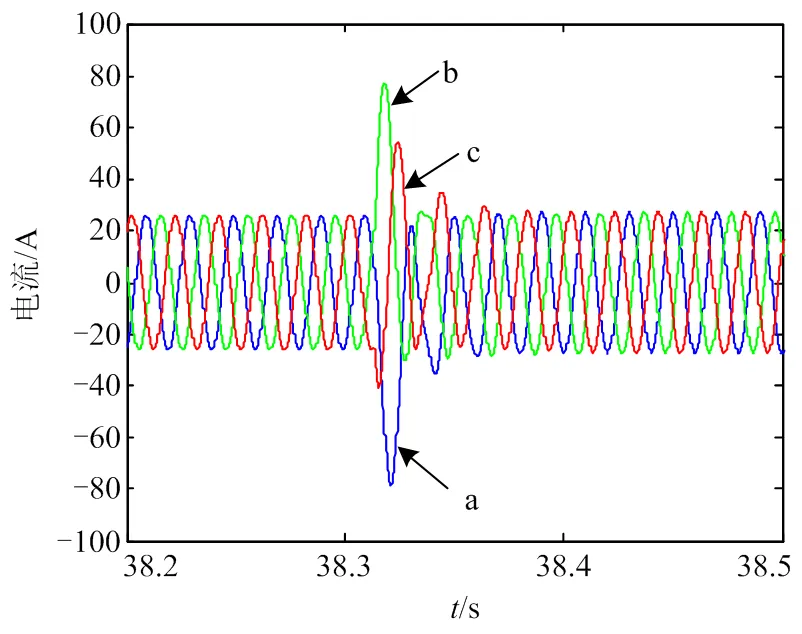
图10 电流波形
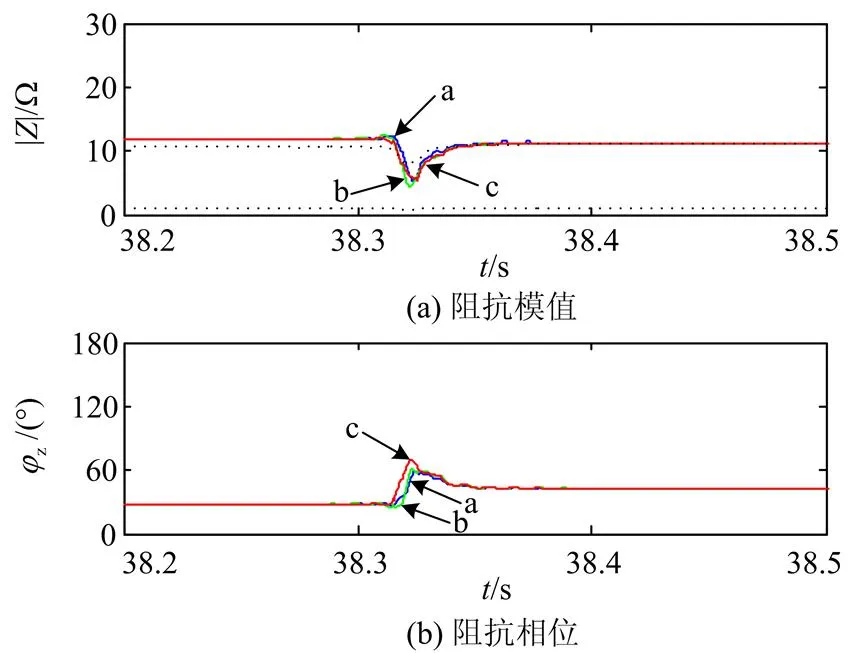
图11 阻抗模值和相位
4 结论
本文基于电压暂降信号的复阻抗特性,通过运用Hilbert变换,结合超限判别的方法,对其进行准确定位和检测。在电压暂降发生时,电压下降电流上升,导致阻抗模值大幅跌落,使电压暂降的数值变化更易于判别;阻抗相位用于辅助分析。由仿真实验结果可知,该方法可以准确地定位电压暂降的发生以及检测其持续时间,并且具有计算简单、检测精度高的特点,在实际应用中具有广泛的前景。
[1] 肖湘宁, 韩民晓, 徐永海, 等. 电能质量分析与控制[M]. 北京: 中国电力出版社, 2010.
[2] 程浩忠, 艾芊, 张志刚, 等. 电能质量[M]. 北京: 清华大学出版社, 2006.
[3] BOLLEN M H. Understanding power quality problems[M]. New Jersey: Wiley-IEEE Press, 1999.
[4] 杨达亮, 卢子广, 杭乃善. 新型单相电压暂降实时检测方法及实现[J]. 电力自动化设备, 2015, 35(2): 110-113.
YANG Daliang, LU Ziguang, HANG Naishan. Method and realization of real-time single-phase voltage sag detection[J]. Electric Power Automation Equipment, 2015, 35(2): 110-113.
[5] 肖助力, 龚仁喜, 陈双. 一种改进不完全S变换的电压暂降检测方法[J]. 电力系统保护与控制, 2015, 43(9): 62-68.
XIAO Zhuli, GONG Renxi, CHEN Shuang. Detection of voltage age by a modified incomplete S-transform[J]. Power System Protection and Control, 2015, 43(9): 62-68.
[6] 赵莹, 赵川, 叶华, 等. 应用主成分分析约减电压暂降扰动源识别特征的方法[J]. 电力系统保护与控制, 2015, 43(13): 105-110.
ZHAO Ying, ZHAO Chuan, YE Hua, et al. Method to reduce identification feature of different voltage sag disturbance source based on principal component analysis[J]. Power System Protection and Control, 2015, 43(13): 105-110.
[7] 陈国栋, 朱淼, 蔡旭, 等. 一种软件锁相环和电压跌落检测新算法[J]. 中国电机工程学报, 2014, 34(25): 4385-4394.
CHEN Guodong, ZHU Miao, CAI Xu, et al. A new algorithm for software phase locked-loop and voltage sag detection[J]. Proceedings of the CSEE, 2014, 34(25): 4385-4394.
[8] 黄小庆, 曹阳, 吴卫良, 等. 考虑电压暂降指标的电压协调控制方法研究[J]. 电力系统保护与控制, 2015, 43(22): 147-154.
HUANG Xiaoqing, CAO Yang, WU Weiliang, et al. Research on voltage coordination control method considering voltage sag index[J]. Power System Protection and Control, 2015, 43(22): 147-154.
[9] 唐轶, 陈嘉, 樊新梅, 等. 基于扰动有功电流方向的电压暂降源定位方法[J]. 电工技术学报, 2015, 30(23): 102-109.
TANG Yi, CHEN Jia, FAN Xinmei, et al. A method for detecting voltage sag sources based on disturbance active current direction[J]. Transactions of China Electrotechnical Society, 2015, 30(23): 102-109.
[10] 薛尚青, 蔡金锭. 基于Sage-Husa卡尔曼滤波的三相电压暂降检测[J]. 电力系统自动化, 2012, 36(1): 71-74.
XUE Shangqing, CAI Jinding. Three-phase voltage sag detection based on Sage-Husa Kalman filtering[J]. Automation of Electric Power Systems, 2012, 36(1): 71-74.
[11] COSTA F B, DRIESEN J. Assessment of voltage sag indices based on scaling and wavelet coefficient energy analysis[J]. IEEE Transactions on Power Delivery, 2013, 28(1): 336-346.
[12] HE Shunfan, LI Kaicheng, ZHANG Ming. A new transient power quality disturbances detection using strong trace filter[J]. IEEE Transactions on Instrumentation and Measurement, 2014, 63(12): 2863-2871.
[13] MANIKANDAN M S, SAMANTARAY S R, KAMWA I. Detection and classification of power quality disturbances using sparse signal decomposition on hybrid dictionaries[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64(1): 27-38.
[14] 彭启琮, 邵怀宗, 李明奇, 等. 信号分析导论[M]. 北京: 高等教育出版社, 2010.
[15] 程志友, 王家琦, 左靖坤. 基于ASW-ESPRIT的电能质量扰动分析[J]. 电力系统保护与控制, 2013, 41(2): 132-137.
CHENG Zhiyou, WANG Jiaqi, ZUO Jingkun. Power quality disturbance analysis based on ASW-ESPRIT[J]. Power System Protection and Control, 2013, 41(2): 132-137.
[16] 黄长蓉. Hilbert变换及其应用[J]. 成都气象学院学报, 1999, 14(3): 273-276.
HUANG Changrong. Hilbert transform and its applications[J]. Journal of Chengdu Institute of Meteorology, 1999, 14(3): 273-276.
(编辑 魏小丽)
A voltage sag detection method based on complex impedance
CHENG Zhiyou1, 2, WANG Xuefei2, 3, XU Jia2
(1. Power Quality Engineering Research Center, Ministry of Education, Hefei 230601, China; 2. School of Electronics and Information Engineering, Anhui University, Hefei 230601, China; 3. Anhui Sun Create Electronic Co., Ltd., Hefei 230088, China)
Voltage sag is currently one of the most important power quality problems in power system, which has become increasingly a focus of attention in society. Due to the defects of traditional algorithm that has complex operation and poor precision, this paper proposes a voltage sag detection method based on complex impedance. Firstly, Hilbert transform is used to construct the analytic signals for detected voltage and current signals separately, and then their corresponding complex impedance will be calculated, making use of the specialty that when the voltage sag happened, its impedance and phase angle will jump at the same time, and combining overrun discriminator, the proposed method can locate the occurrence time of voltage sag, and detect its time duration. Finally, the effectiveness of the proposed method in this paper is verified by several experiments, the experimental results show that this method has high accuracy and easy to distinguish, it has wide promotional value.
Hilbert transform; complex impedance; voltage sag; power quality
10.7667/PSPC150709
安徽省高等学校省级自然科学研究项目(J01010127)
2015-04-27;
2015-11-19
程志友(1972-),男,博士,教授,研究方向为电能质量分析、检测和评估;E-mail: czy@ahu.edu.cn
王雪菲(1990-),女,通信作者,助理工程师,研究方向为电能质量分析、检测和评估;E-mail: 377811040@qq.com
徐 佳(1987-),男,硕士研究生,研究方向为电能质量分析、检测与评估。
