极大平面图的结构与着色理论(1)色多项式递推公式与四色猜想

许 进



极大平面图的结构与着色理论(1)色多项式递推公式与四色猜想

许 进*

(北京大学信息科学技术学院 北京 100871)(北京大学高可信软件技术教育部重点实验室 北京 100871)

该文给出了极大平面图的色多项式递推计算公式：若,是中轮心为，轮圈为的4-轮，则，其中,；若,是中为轮心，以为轮圈的5-轮，则，其中,，“”表示收缩运算；进而讨论了使用公式证明四色猜想的应用：将四色猜想转化成研究一种特殊图类：4-色漏斗型伪唯一4-色极大平面图。

四色猜想；极大平面图；色多项式；伪唯一4-色平面图；4-色漏斗

1 引言

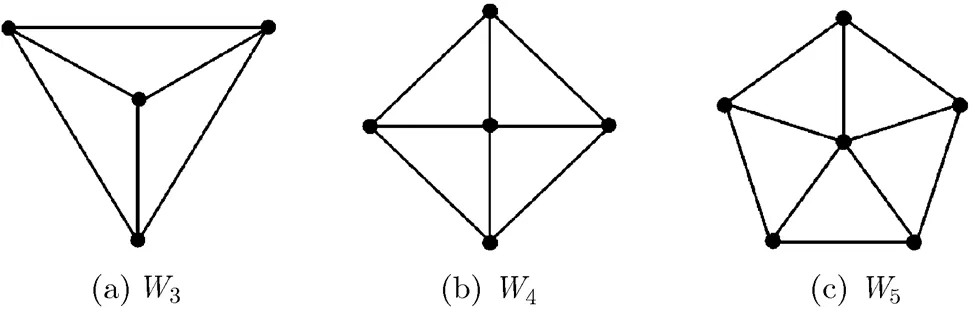
图1 轮图示例

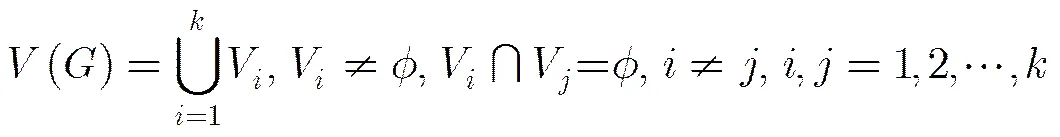
如果一个图能够画在平面上使得它的边仅在顶点相交，则称这个图为平面图。平面图的这样一种画法称为它的一个平面嵌入，本文所研究的平面图均是指基于它的一个平面嵌入下的平面图。对于一个平面图，如果只要任何两个不相邻的顶点之间再加一条边，其平面性一定被破坏，则称该平面图为极大平面图。若一个平面图的每个面(包括无穷面)都由3条边界组成，则称该平面图为三角剖分图。易证，极大平面图和三角剖分图是等价的。

无论是理论上还是应用上，平面图都是一类非常重要的图类。理论上，著名的4-色猜想，唯一4-色平面图猜想，9-色猜想，以及3-色问题等[1]不仅在图论领域，乃至整个数学界都具有重大影响；从应用的角度来讲，平面图理论可直接应用于电路布线[2]，信息科学[3]等领域。

由于著名的4-色猜想的研究对象可归为极大平面图，因此，100多年来，关于极大平面图的研究吸引了众多的学者，围绕着4-色猜想，相继研究了诸如度序列、构造、着色特性、可遍历性，生成运算等诸多方面[4]。并且在研究过程中，提出了诸如唯一4-色极大平面图猜想以及9-色猜想等，它们也逐渐构成了极大平面图着色理论的核心研究目标。

在4-色猜想的研究过程中，从1879年KEMPE的“证明”[5]，到HEAWOOD的反例[6]，再到1976年由HAKEN与APPEL给出的“计算机证明”，主要集中在“寻找可约的不可避免集”这一种研究方法上。利用这种方法通过电子计算机找到了1936个可约的不可避免集，证明了四色猜想成立；1997年由ROBERTSON, SANDERS, SEYMOUR和THOMAS等人找出了633个可约构形的不可避免集，简化了四色猜想的计算机证明。

“不可避免集”的研究起源于1904年WERNICKE的工作[12]；“可约构形”是BIRKHOFF于1913年提出来的[13]。在利用“寻找可约的不可避免集”这种思想的证明过程中，德国数学家HEESCH做出了不可磨灭的贡献，他发现了证明可约性的一种方法放电法[14]，并确信此方法可解决四色猜想，为1976年利用电子计算机求解四色猜想奠定了基础。另外，还有不少学者在此方法上作出贡献，诸如FRANKLIN, REYNOLDS[17], WINN[18], ORE和STEMPLE[19], MAYER[20]。

人是无法通过手工对不可避免集和可约构形进行验证的，因此，如何给出数学证明仍是一个尚待解决的数学难题。

除了基于“可约的不可避免集”的证明方法外，另一个具有影响的证明方法是基于假设：“每个3-正则3-连通的平面图都有哈密顿圈”的条件给出的“证明”，该证明是由TAIT于1880年给出[21]。由于这个假设是错的，其证明自然是错的。这个错误的假设是PETERSEN[22]发现的，但直到1946年，TUTTE才找到该证明的反例[23]。后来，GRINBERG[24]在1968年找到了一个必要条件，由此可产生很多3-正则3-连通的非HAMILTON平面图。虽然TAIT的证明是错的，但TAIT的工作对于图论的研究，特别是边着色理论产生了深远的影响。用表示对标定图的顶点用种颜色进行着色时具有的着色数目。显然，当时，即该图没法被着色时，；但当，这种着色的数目肯定存在，即。对于任意一个平面图，当时，若能够证明，则就相当于证明了四色猜想！这就是BIRKHOFF在1912年提出用来证明四色猜想的一种方法[25,26]。后来发现，是一个关于的多项式，故称为图的色多项式。目前，图的色多项式已经成为了图论学科中一个很有魅力的独立分支[27]。遗憾的是，BIRKHOFF的愿望至今尚未实现。对色多项式的研究引起了众多学者的极大兴趣。关于这方面研究较为深入的文章与专著可参阅文献[25-31]，其中文献[28]的结果最为诱人，证明了：当(其中)时，。此结果与四色猜想有点“擦肩而过”的遗憾，因为只要能够证明，则四色猜想成立。

在计算给定图的色多项式方面，一个最为基本的公式是所谓的缩边递推公式。

缩边递推公式[25]若图是简单图，则对图的任何边，都有

另外，本文作者在文献[32,33]分别给出缩点递推公式以及图与补图的色多项式等。

可能是因为TUTTE的工作很漂亮，以及TUTTE在学术界的地位，人们认为以图的色多项式为工具解决四色猜想似乎不可能，本文下述的工作重新“燃起”了利用图的色多项式作为工具之一来证明四色猜想的希望。

2 色多项式的缩轮递推公式

为方便，先给出如下2个引理：

引理1[26]对任何无自环的平面图,是4-可着色的当且仅当

引理2[25,27]若图是子图与的并，且与的交为-阶完全图，则

图2 一个含有4度顶点的极大平面图

即

从而本定理获证。

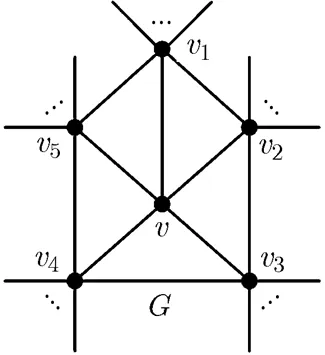
图3 一个含有5度顶点的极大平面图

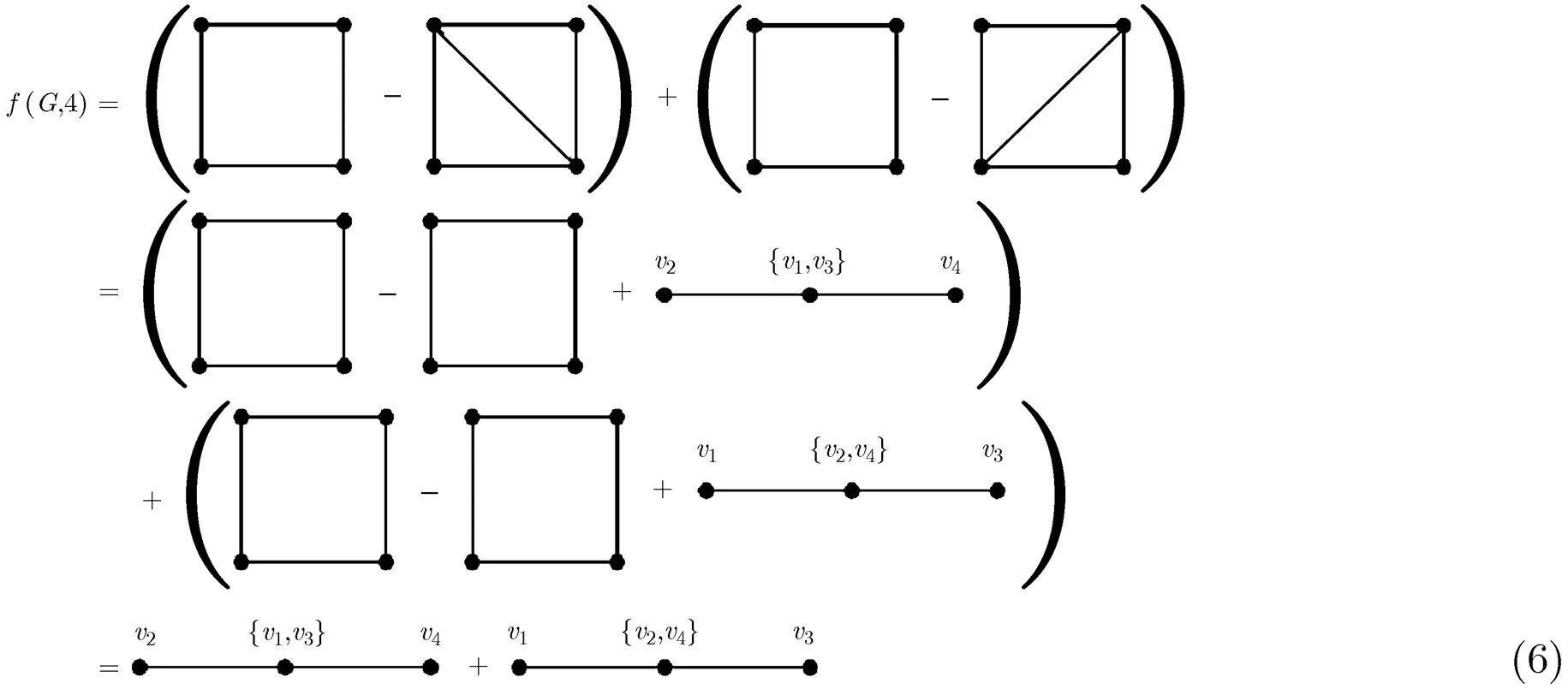
由引理2，式(10)最后一个等号右端第1个图的色多项式应该为。因此，我们有

注意到式(13)等号右端第1个括号内的第1个图实际上就是图；第2个括号内的第1个图实际上是；第3个括号内的第1个子图实际上是，从而本定理获证。

3 定理2给出了证明四色猜想的一种思路

众所周知，四色猜想的最终证明一般需采用数学归纳法，且按照最小度进行分类。当最小度为时，由归纳法容易证明，但当时，至今数学方法尚未给出证明。下面，给出一种基于定理1和定理2的四色猜想证明思路：

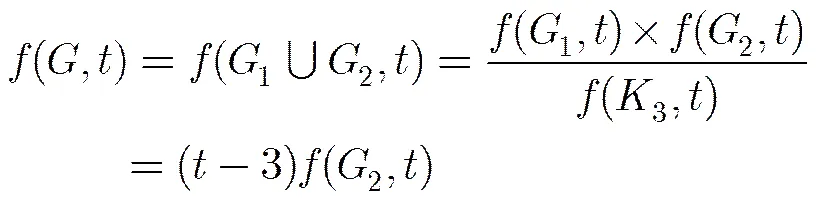
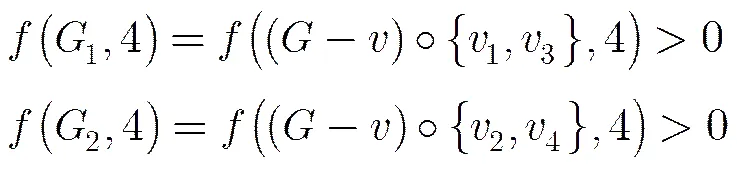
关键是下面的情况3。

顶点数最少的最小度为5的极大平面图是正20面体，如图4(a)所示，具有12个顶点，它显然是4-可着色的。不存在13阶的最小度为5的极大平面图。故对顶点数，且最小度为5的极大平面图

第1种思路：显然，由于

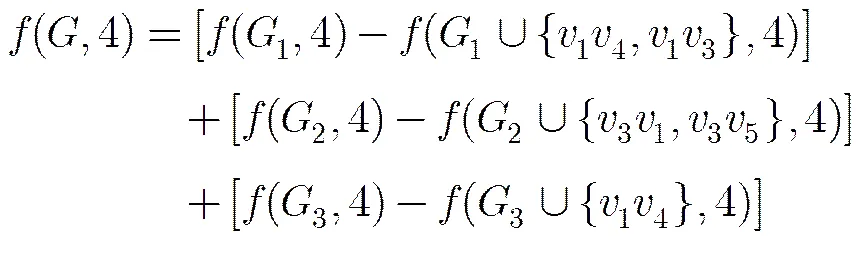
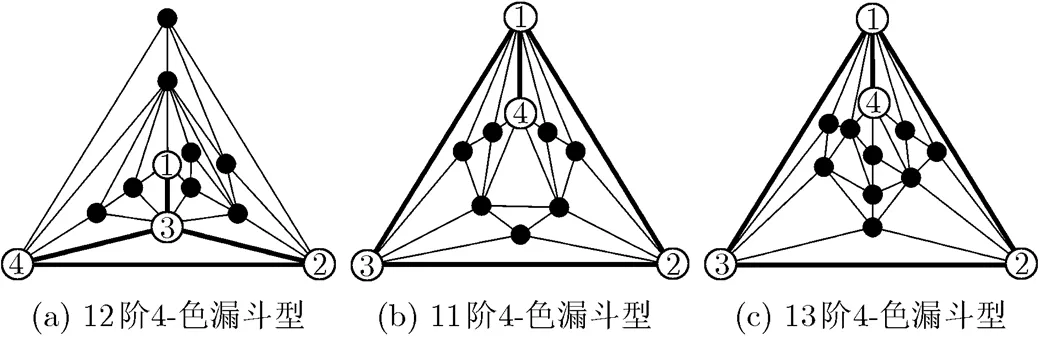
图5 3个4-色漏斗型-伪唯一4-色极大平面图

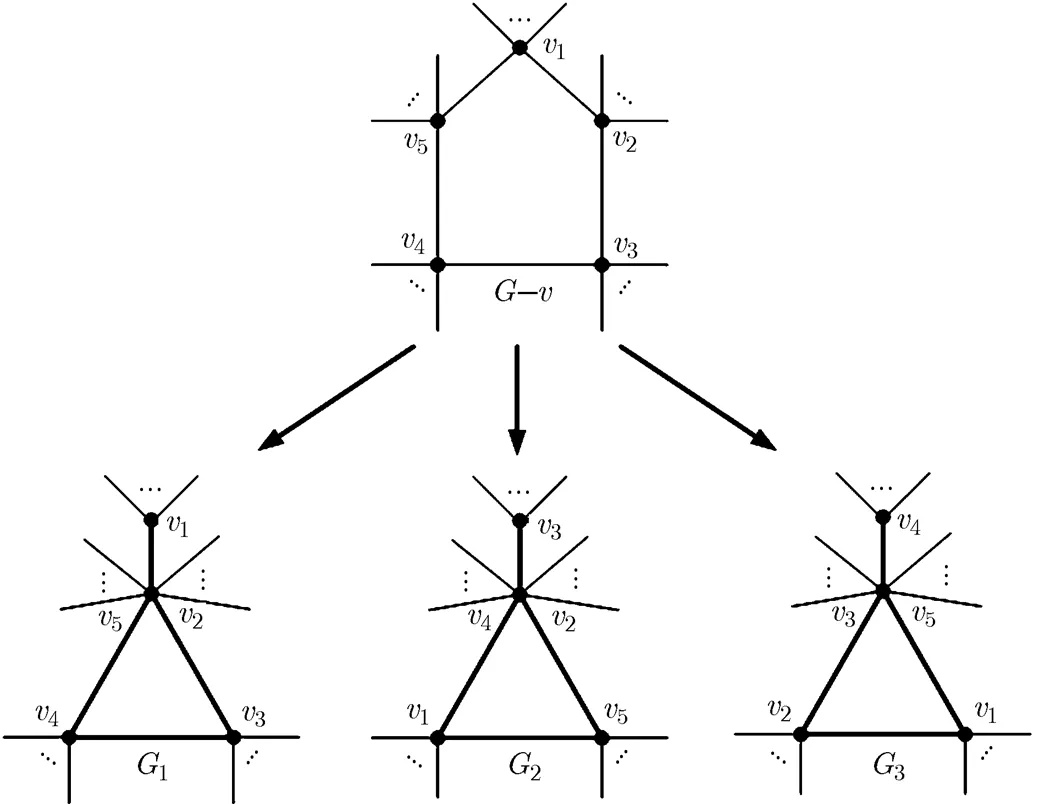
图6 3个漏斗子图的产生过程说明示意图

由此给出证明四色猜想的第2种思路：对于一个最小度为5的极大平面图中的5-轮，对应于,,的3个漏斗子图,,至少有一个为非4-色漏斗。例如，我们视图5(a)是由图7中的5-轮按图6所示的方法获得的，容易证明，按图6中所示的方法获得的其余两个极大平面图不含4-色漏斗。

4 结束语

本文给出了求解极大平面图的一种色多项式的递推公式，由该公式发现：第一，证明四色猜想的两种思路；第二，导出了一种将图的着色与构造相融合的构造极大平面图的方法扩缩运算系统，如图5(a)就是通过所谓的扩5-轮运算获得图7中所示的极大平面图，或者说，图7中所示的极大平面图是通过缩5-轮运算得到图5(a)。极大平面图的扩缩运算系统的详细研究将在本系列文章的第2篇中给出。

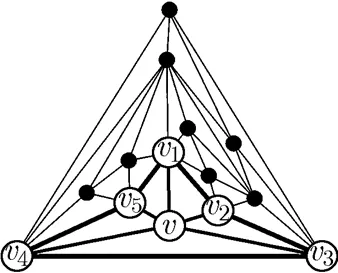
图7 可收缩成图5中第1个图的极大平面图

致谢：本文在完成过程中相继与我的5位图论专业学生：朱恩强与李泽鹏博士后；刘小青与王宏宇博士生以及周洋洋硕士生等进行了多次有益的讨论，在此表示感谢。

[1] JENSEN T R and TOFT B. Graph Coloring Problems[M]. New York: John Wiley & Sons, 1995: 48-49

[2] DÍAZ J, PETIT J, and SERNA M. A survey of graph layout problems[J]., 2002, 34(3): 313-355.

[3] BRODER A, KUMAR R, MAGHOUL F,. Graph structure in the Web[J]., 2000, 33(1-6): 309-320.

[4] 许进, 李泽鹏, 朱恩强. 极大平面图的研究进展[J]. 计算机学报, 2015, 38(7): 1680-1704.

XU Jin, LI Zepeng, and ZHU Enqiang. Research progress on the theory of maximal planar graphs[J]., 2015, 38(7): 1680-1704.

[5] KEMPE A B. On the geographical problem of the four colors [J]., 1879, 2(3): 193-200.

[6] HEAWOOD P J. Map colour theorem[J]., 1890, 24: 332-338.

[7] APPEL K and HAKEN W. The solution of the four-color map problem[J]., 1977, 237(4): 108-121.

[8] APPEL K and HAKEN W. Every planar map is four colorable, I: Discharging[J]., 1977, 21(3): 429-490.

[9] APPEL K, HAKEN W, and KOCH J. Every planar map is four-colorable, II: Reducibility[J]., 1977, 21(3): 491-567.

[10] ROBERTSON N, SANDERS D P, SEYMOUR P,. A new proof of the four colour theorem[J]., 1996, 2: 17-25.

[11] ROBERTSON N, SANDERS D P, SEYMOUR P D,. The four color theorem[J].,, 1997, 70(1): 2-44.

[13] BIRKHOFF G D. The reducibility of maps[J]., 1913, 35(2): 115-128.

[14] HEESCH H. Untersuchungen Zum Vierfarbenproblem[M].Mannheim/Wien/ZÄurich: Bibliographisches Institut, 1969: 4-12.

[15] FRANKLIN P. The four color problem[J].,1922, 44(3): 225-236.

[16] FRANKLIN P. Note on the four color problem[J]., 1938, 16: 172-184.

[17] REYNOLDS C. On the problem of coloring maps in four colors[J]., 1926-27, 28(1-4): 477-492.

[18] WINN C E. On the minimum number of polygons in an irreducible map[J]., 1940, 62(1): 406-416.

[19] ORE O and STEMPLE J. Numerical calculations on the four-color problem[J]., 1970, 8(1): 65-78.

[20] MAYER J. Une propriètè des graphes minimaux dans le problµeme des quatre couleurs[J].,, 1978, 260: 291-295.

[21] TAIT P G. Remarks on the colouring of maps[J]., 1880, 10: 501-516.

[22] PETERSEN J. Surle théorème de Tait[J]., 1898, 5: 225-227.

[23] TUTTE W T. On Hamiltonian circuits[J]., 1946, 21: 98-101.

[24] GRINBERG E J. Plane homogeneous graphs of degree three without Hamiltonian circuits[J]., 1968, 5: 51-58.

[25] BIRKHOFF G D. A determinantal formula for the number of ways of coloring a map[J]., 1912, 14: 42-46.

[26] BIRKHOFF G D and LEWIS D. Chromatic polynomials[J].

, 1946, 60:

355-451.

[27] DONG F M, KOH K M, and TEO K L. Chromatic Polynomials and Chromaticity of Graphs[M].World Scientific, Singapore, 2005: 23-215.

[28] TUTTE W T. On chromatic polynomials and the golden ratio[J]., 1970, 9(3): 289-296.

[29] TUTTE W T. Chromatic sums for planar triangulations, V: Special equations[J]., 1974, 26: 893-907.

[30] READ R C. An introduction to chromatic polynomials[J]., 1968, 4(1): 52-71.

[31] WHITNEY H. On the coloring of graphs[J]., 1932, 33(4): 688-718.

[32] XU Jin. Recursive formula for calculating the chromatic polynomial of a graph by vertex deletion[J]., 2004, 24(4): 577-582.

[33] XU Jin and LIU Z. The chromatic polynomial between graph and its complementAbout Akiyama and Hararys,open problem[J]., 1995, 11: 337-345.

[34] ZYKOV A A. On some properties of linear complexes[J]., 1949, 24(66): 163-188 (in Russian);, 1952, 79.

许 进： 男，1959年生，教授，主要研究领域为图论与组合优化、生物计算机、社交网络与信息安全等.

Foundation Items: The National 973 Program of China (2013CB329600), The National Natural Science Foundation of China (61472012, 6152046, 6152012, 61572492, 61372191, 61472012)

Theory on the Structure and Coloring of Maximal Planar Graphs(1)Recursion Formulae of Chromatic Polynomial and Four-Color Conjecture

XU Jin

(School of Electronics Engineering and Computer Science, Peking University, Beijing 100871, China)(Key Laboratory of High Confidence Software Technologies, Peking University, Beijing 100871, China)

In this paper, two recursion formulae of chromatic polynomial of a maximal planar graphare obtained: when, letbe a 4-wheel ofwith wheel-centerand wheel-cycle, then; when, leta 5-wheel ofwith wheel-centerand wheel-cycle, then,,, where“”denotes the operation of vertex contraction. Moreover, the application of the above formulae to the proof of Four-Color Conjecture is investigated. By using these formulae, the proof of Four-Color Conjecture boils down to the study on a special class of graphs, viz., 4-chromatic-funnel pseudo uniquely-4-colorable maximal planar graphs.

Four-Color Conjecture; Maximal planar graphs; Chromatic polynomial; Pseudo uniquely-4-colorable planar graphs; 4-chromatic-funnel

O157.5

A

1009-5896(2016)04-0763-17

10.11999/JEIT160072

2016-01-15；改回日期：2016-01-20；网络出版：2016-01-22

许进 jxu@pku.edu.cn

国家973规划项目(2013CB329600)，国家自然科学基金(61472012, 6152046, 6152012, 61572492, 61372191, 61472012)