多基地雷达中双门限CFAR检测算法

胡勤振 苏洪涛 周生华 刘子威



多基地雷达中双门限CFAR检测算法

胡勤振 苏洪涛*周生华 刘子威

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

针对多基地雷达系统，该文为解决传统集中式检测算法数据传输率大的问题，根据广义似然比检测算法和自适应匹配滤波算法，提出两种双门限恒虚警率检测器：双门限广义似然比检测器和双门限自适应匹配滤波检测器。首先各个局部雷达站将超过第1门限的局部检验统计量传送到融合中心。然后融合中心根据局部雷达站传送的数据计算融合后的全局检验统计量，并与第2门限比较，得到最终的判决结果。在各空间分集通道的信杂噪比假设相同的条件下，给出了双门限自适应匹配滤波检测器的虚警概率和检测概率的解析表达式。仿真结果表明，两种双门限检测器在低数据率传输时能够保持较好的检测性能。

雷达；双门限检测；恒虚警率检测；广义似然比检测；自适应匹配滤波

1 引言

在多基地雷达系统中，为了获得某种准则下最优的检测性能，通常需要各个雷达站将接收的信号全部传输到融合中心，这无疑需要很大的通信传输带宽[1,2]。如果采用光纤通信，其通信带宽很容易满足数据传输要求，但是这种有线连接方式限制了雷达站的机动性和灵活性。但对于机载雷达和舰载雷达等移动平台，需要通过无线传输将雷达回波数据传送给处理中心。这种情况下，信号传输带宽往往不能满足数据的传输要求，并且随着通信带宽的增加，需要付出更多的代价。

解决数据传输率约束的有效手段是局部雷达站将原始观测数据进行量化[3,4]后传送给融合中心。在传统的分布式检测算法中，局部雷达站将“0/1”判决结果传送给融合中心，融合中心根据相应的融合准则得到最终判决结果[5,6]。基于局部判决的分布式检测算法虽然能有效降低处理中心的计算量和局部雷达站与处理中心之间的数据传输量，但是破坏了原始数据的结构，减少了数据所包含的信息量，从而降低分布式系统的检测性能。为解决将局部判决结果传送到融合中心引起的信息损失问题，人们研究了多种既能减小数据传输量又能增加信息量的分布式检测算法。在文献[7-10]中，讨论了在数据传输率和虚警概率的约束条件下，确定含有信息量更多的观测区域，并将落入该区域的观测传送给融合中心，使检测性能或目标函数达到最优。然而，当检验统计量的统计特性很难给出时，上述根据约束条件解优化方法计算量大，并且很难给出闭式解。在文献[11]中，局部雷达站根据观测量含有信息量的大小按顺序传送信号，当融合中心得到判决时，将控制信息反馈给局部雷达站，终止数据的传送，从而降低数据传输量，同时保证与无通信带宽约束条件具有相同的虚警概率和漏警概率。但这种方法需要严格控制雷达站的数据传送时间，同时需要反馈，系统较为复杂。在实际应用中，往往需要一种结构简单，效率更高的检测算法。在杂波和噪声功率已知的情况下，文献[12,13]提出了一种结构简单的双门限检测算法。第1门限由数据传输率约束确定，在奈曼皮尔逊准则下，数据传输率约束可近似由局部虚警概率约束表示。局部雷达站将超过第1门限的观测数据传送到融合中心；融合中心根据奈曼皮尔逊准则得到似然比检测器，并由第2门限保证全局虚警概率。然而，上述检测算法是在已知噪声功率且无杂波背景条件下展开讨论的，不适用于存在未知功率的杂波和噪声的情况。

本文重点研究在杂波和噪声功率未知和数据传输率约束条件下的双门限恒虚警率检测(Double Threshold Constant False Alarm Rate, DT-CFAR)方法。根据广义似然比检测(Generalized Likelihood Ratio Test, GLRT)算法[14]或自适应匹配滤波(Adaptive Matched Filter, AMF)算法[15]，本文提出了两种DT-CFAR检测器：DT-GLRT检测器和DT- AMF检测器。在杂波加噪声功率未知的情况下，各个局部雷达站采用GLRT算法或AMF算法进行第1门限检测，并将超过第1门限的观测数据传送到融合中心。融合中心根据局部雷达站传送的数据计算融合后的GLRT或AMF，并与第2门限比较，得到最终的判决结果。本文详细推导了两种不同检测器在融合中心的检验统计量的具体表达式。经过分析可以看出，各空间分集通道只需要将超过第1门限的局部检验统计量传送给融合中心。在各个通道信噪比相同条件下，给出了DT-AMF算法的检测概率和虚警概率解析表达式。最后对数据传输率对检测性能的影响进行了仿真分析。

2 信号检测模型

双门限恒虚警率检测方法如图1所示，图中，检测单元附近为保护单元。在第个空间分集通道中，根据局部虚警概率fa,n设置第1门限。

图1 DT-CFAR检测器流程图

在雷达信号传输过程中，数据传输率定义为每秒中传输的数据量，单位是bit/s。假设系统的采样频率为Hz，采样量化位数为bit。在集中式检测算法中，每个空间分集通道的数据传输率可近似表示为bit/s。数据传输率可通过第1门限控制。在各空间分集通道中，回波数据中大部分为杂波和噪声等无用信号，因此数据传输量可近似为虚警点数。因此经过第1门限处理后，每个空间分集通道的数据传输率约为sfa,nbit/s。

3 双门限CFAR检测器和性能分析

GLRT算法的本质是对似然函数中的未知参数进行最大似然估计。GLRT算法[14]是将参考单元信号和检测单元信号的联合概率密度函数作为似然函数，似然函数中的未知参数为杂波加噪声功率，杂波加噪声功率水平进行最大似然估计需要同时考虑参考单元和待检测单元数据。然而，在AMF算法[15]中，先假设杂波加噪声功率已知，似然函数为检测单元的概率密度函数。得到似然比后，利用参考单元估计出的杂波加噪声功率水平代入似然比中。下面主要分析两种算法的检测结构和性能。

3.1 DT-GLRT检测

假设各个空间分集通道的局部虚警概率相同，即fa,1==fa,N=fa，经过简单推导，可得

其中，

将式(12)代入到式(6)，并取对数运算，DT-GLRT检测器可以表示为

3.2 DT-AMF检测

与GLRT算法不同，AMF算法首先假设杂波加噪声功率已知，待检测单元按照似然比的形式给出。然后将由参考单元估计的杂波加噪声功率带入似然比中。第个空间分集通道的AMF可表示为

其中，

代入到式(6)，并取对数运算，DT-AMF检测器可以表示为

因此，全局虚警概率可表示为

可以看出，虚警概率与杂波加噪声功率无关，只与局部虚警概率、空间分集通道的个数和参考单元个数有关，因此DT-AMF检测器具有CFAR特性。

在各个空间分集通道的信杂噪比不同的条件下，需要计算独立但不同参数的广义帕累托分布求和，即加权的独立Pareto分布求和的统计特性，目前还无法给出显式表达式。

由式(13)和式(19)中可以看出，无论是DT- GLRT检测器还是DT-AMF检测器，其融合中心的全局检验统计量均为的函数。因此，各空间分集通道可以直接传送统计变量而不是观测数据给融合中心，然后融合中心根据相应的检测融合准则融合。实际上，在各空间分集通道中，统计变量为单元平均CFAR检测器的检验统计量。因此，在各空间分集通道中，局部雷达站可以先进行单元平均CFAR检测，然后将过第1门限的检验统计量传送给融合中心。这样，在降低了数据量传输的同时也降低了融合中心的计算复杂度。

4 数值仿真及分析

为了分析数据传输率对检测性能的影响，在此进行数值仿真实验。仿真参数设置如下：两个分布式雷达发射站发射正交波形，有两个分布式雷达接收站，因此共有个空间分集通道，每个空间分集通道的参考单元个数。仿真中，总的信杂噪比定义为各空间分集通道的信杂噪比之和。

在各通道信杂噪比相同情况下，全局虚警概率与局部虚警概率、第2门限之间的关系如图2所示。总的信杂噪比设置为10 dB，各空间分集通道的信杂噪比相同。图中横坐标为第2门限，纵坐标为全局虚警概率。从图中可以看出，在给定局部虚警概率条件下，当第2门限小于某一临界值时，全局虚警概率保持不变，即只要融合中心接收到局部雷达站的数据，就判为，此时第2门限不起作用。该临界值的取值为当且时，式(13)和式(19)左右相等时计算得到的的值。对于DT-GLRT检测器，的临界值为

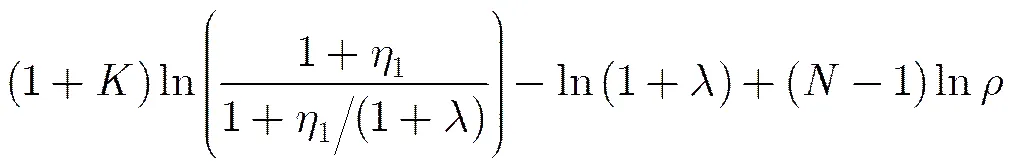
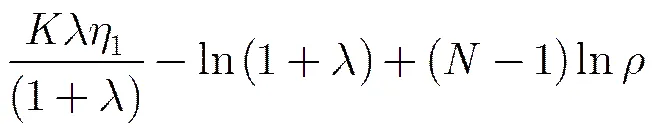
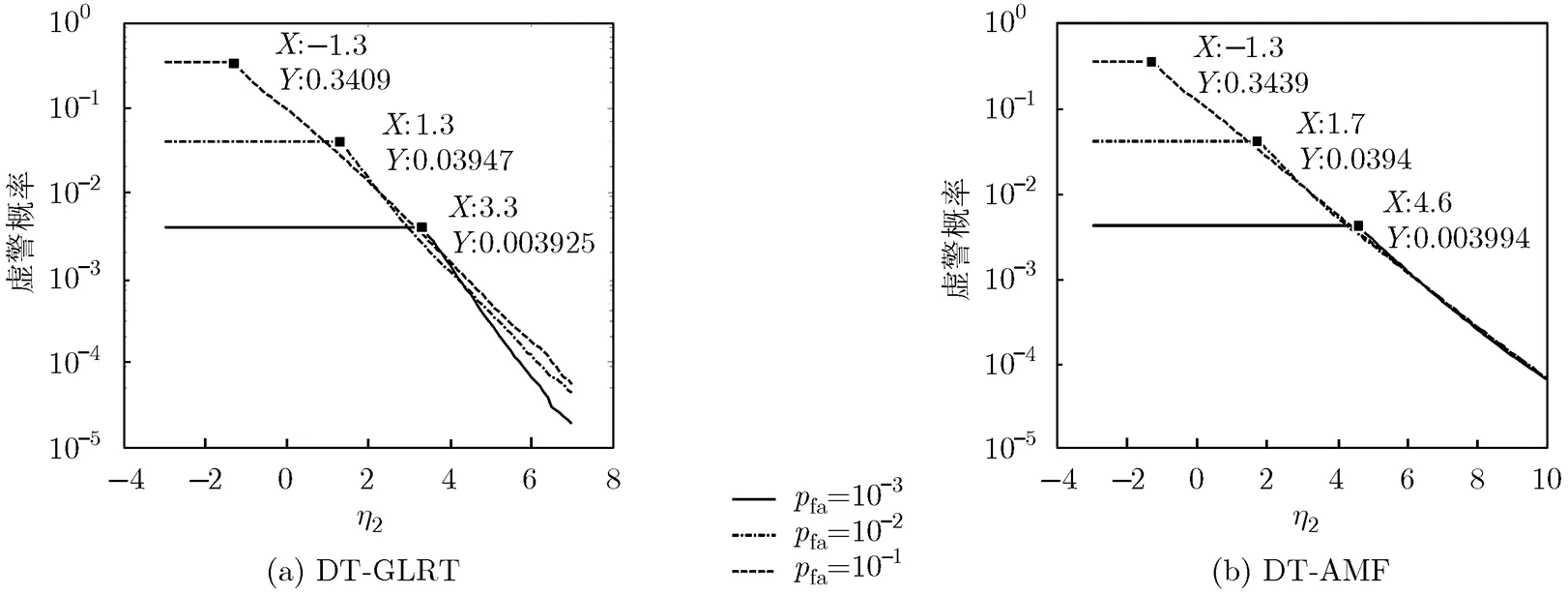
图2 全局虚警概率与局部虚警概率、第2门限之间的关系

数据传输率约束对检测性能的影响如图3所示。全局虚警概率设置为, SCNR表示总的信杂噪比，横坐标为局部虚警概率，纵坐标为检测概率。图3(a)和图3(b)分别为各通道信杂噪比相同和不同两种情况，图3(b)中各通道信杂噪比之比设为[100 100 1 1]。从图中可以看出，随着局部虚警概率的减小，DT-GLRT检测器和DT-AMF检测器的检测性能下降缓慢。因此在这是因为，当局部虚警概率越小，第1门限越高，局部雷达站传给融合中心的数据信息越少，因此检测性能越差。还可以发现，DT-GLRT的检测性能要优于DT-AMF，然而随着局部虚警概率的减小，二者的检测性能逐渐接近。可以看出，两种情况下，在局部虚警概率变大时，其检测性能损失很小，因此，双门限检测器在低数据率传输时能够保持较好的检测性能。对比图3(a)和图3(b)可以看出，在低SCNR下，信杂噪比不同情况下的检测性能要优于信杂噪比相同的情况；在高SCNR下，在第1门限小于临界值时，信杂噪比相同情况下的检测性能优于信杂噪比不同的情况，但当第1门限超过临界值时，信杂噪比不同情况下的检测性能要优于信杂噪比相同的情况。

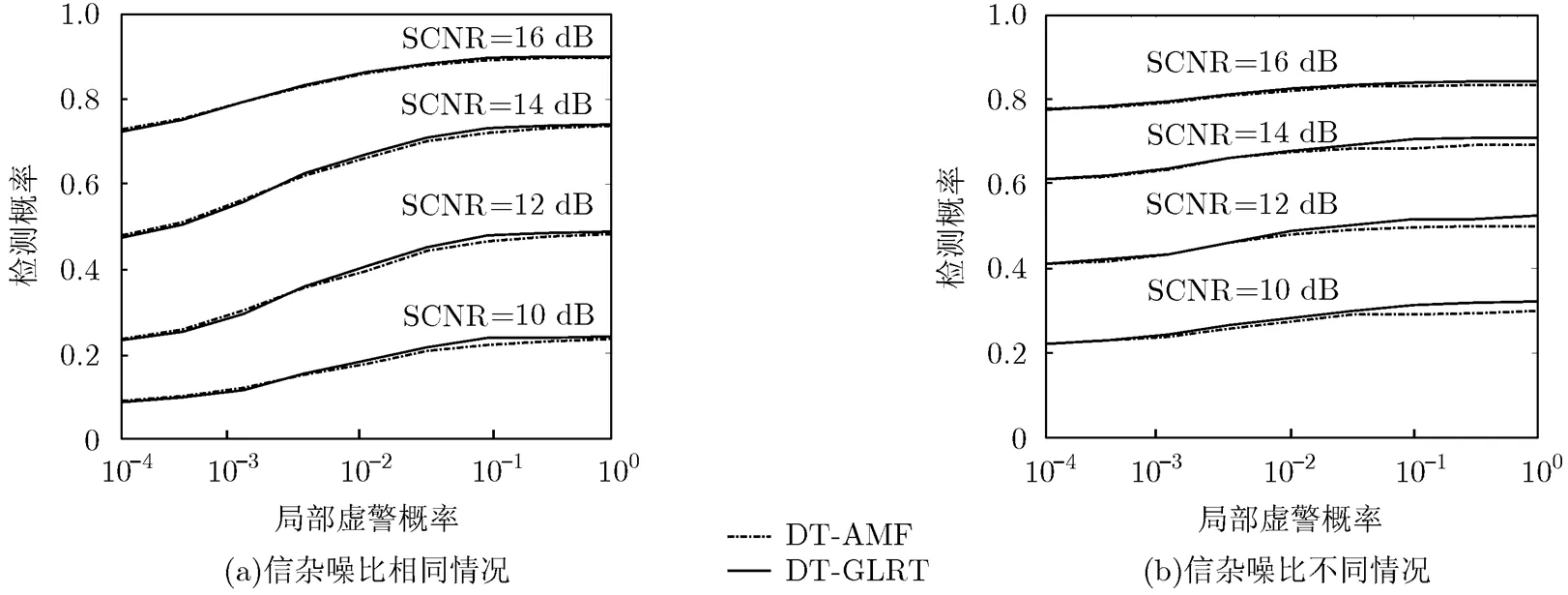
图3 检测概率随局部虚警概率的变化

图4分析了在不同局部虚警概率下，检测概率随信杂噪比变化的性能。全局虚警概率设置为,fa=1表示第1门限，即采用集中式检测算法，此时具有最优的检测性能。从图中可以看出，与集中式检测算法相比，当时，双门限检测器只有很小的信杂噪比损失；当时，即在数据传输量降低100倍时，双门限检测器有不到1 dB的信杂噪比损失。同时，两种双门限检测器性能上要优于分布式“或”准则(OR rule)检测器。因此，双门限检测器在低数据率传输时能够保持较好的检测性能。

图4 检测概率随SCNR的变化

图5给出了各通道信杂噪比相同和不同两种情况下的检测性能比较，各通道信杂噪比不同时，各通道信杂噪比之比设为[100 100 1 1]，图5(a)和图5(b)中，局部虚警概率分别设置为和。通过比较可以看出，在低SCNR条件下，信杂噪比不同情况下的检测性能要优于信杂噪比相同的情况；在高SCNR下，信杂噪比相同情况下的检测性能优于信杂噪比不同的情况。

图5 不同局部虚警概率下性能比较

从图3，图4和图5中可以看出，本文提出的两种检测器，DT-GLRT的检测性能要略优于DT- AMF。文献[18]中的1维信号集中式检测算法虽然未使用第1门限处理，得到的似然比检测器与本文的GLRT检测器结构相似，其似然比检测器的一阶近似于AMF检测器结构相似，其仿真结果可以看出其似然比检测器要优于似然比检测器的一阶近似。在空时2维自适应检测问题中，对于单基地雷达系统[15,19]，存在较大的临界值，当信噪比高于该临界值时，AMF检测器的检测性能会优于GLRT检测器。对于多基地雷达系统[19]，得到的仿真结果是GLRT的检测性能优于AMF检测器，但文献作者认为，可能存在该临界值，只是随着通道数的增加，该临界值变得非常大。其实在1维信号处理中，当在只有一个道数的情况下，DT-AMF检测器与DT-GLRT器具有相同的检验统计量，此时，两种检测器的检测性能相同，这是与文献[15,19]的不同之处。

5 结论

双门限检测器剔除掉信息量小的数据并将含有更多信息的数据传输到融合中心进行融合检测。因此，双门限检测器在有效降低局部雷达站向融合中心传输的数据量的同时，能保证较好的检测性能。在杂波和噪声功率未知的情况下，结合GLRT算法和AMF算法，本文给出了两种DT-CFAR检测器：DT-GLRT检测器和DT-AMF检测器。各空间分集通道只需要将超过第1门限的局部检验统计量传送给融合中心；融合中心根据相应的准则，得到全局检验统计量。在各通道信杂噪比相同的条件下，本文还给出了DT-AMF检测器的虚警概率和检测概率的闭式表达式。由于检测器结构简单，因此对实际系统工程应用具有一定的参考价值。

参考文献

[1] Haimovich A, Blum R, Cimini L,. MIMO radar with widely separated antennas[J]., 2008, 25(1): 116-129. doi: 10. 1109/MSP.2008. 4408448.

[2] Zhou S H and Liu H W. Space-partition-based target detection for distributed MIMO radar[J]., 2013, 49(4): 2717-2729. doi: 10.1109/TAES.2013.6621848.

[3] Xu G, Zhu S Y, and Chen B. Decentralized data reduction with quantization constraints[J]., 2014, 62(7): 1775-1784. doi: 10.1109/TSP. 2014.2303432.

[4] Gao F, Guo L L, Li H B,Quantizer design for distributed GLRT detection of weak signal in wireless sensor networks[J]., 2015, 14(4): 2032-2042. doi: 10.1109/TWC. 2014.2379279.

[5] Barkat M and Varsheny P. Decentralized CFAR signal detection[J]., 1989, 25(2): 141-149. doi: 10.1109/7.18676.

[6] Kailkhura B, Brahma S, Han Y S,Distributed detection in tree topologies with byzantines[J]., 2014, 62(12): 3208-3219. doi: 10.1109/TSP.2014.2321735.

[7] Rago C, Willett P, and Bar-Shalom Y. Censoring sensors: a low-communication-rate scheme for distributed detection[J]., 1996, 32(2): 554-568. doi: 10.1109/7.489500.

[8] Appadwedula S, Veeravalli V, and Jones D. Decentralized detection with censoring sensors[J]., 2008, 56(4): 1362-1373. doi: 10.1109/TSP.2007.909355.

[9] Gul G and Zoubir M. Robust detection under communication constraints[C]. IEEE 14thWorkshop on Signal Processing Advances in Wireless Communications, Darmstadt, 2013: 410-414. doi: 10.1109/SPAWC.2013. 6612082.

[10] He H and Varshney P. Distributed detection with censoring sensors under dependent observations[C]. IEEE International Conference on Acoustic, Speech and Signal Processing, Florence, 2014: 5055-5059. doi: 10.1109/ICASSP. 2014.6854565.

[11] He Q, Blum R, and Rawas Z. Ordering for energy efficient communications for noncoherent MIMO radar networks[C]. IEEE International Conference on Acoustic, Speech and Signal Processing, Kyoto, 2012: 5189-5192. doi: 10.1109/ ICASSP.2012.6289089.

[12] Scharrenbroich M, Zatman M, and Balan R. Cooperative radar techniques: the two-step detector[C]. Conference Record of the 45th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, 2011: 1975-1979. doi: 10.1109/ACSSC.2011.6190370.

[13] Scharrenbroich M, Zatman M, and Balan R. Performance of a practical two-step detector for non- fluctuating targets[C]. IEEE 7th Workshop on Sensor Array and Multichannel Signal Processing, Hoboken, 2012: 313-316. doi: 10.1109/SAM.2012.6250498.

[14] Kelly E. An adaptive detection algorithm[J]., 1986, 22(1): 115-127. doi: 10.1109/TAES.1986.310745.

[15] Robey F, Fuhrmann D, Kelly E,A CFAR adaptive matched filter detector[J]., 1992, 28(1): 208-216. doi: 10.1109/7.135446.

[16] Christian W. Hand-book on Statistical Distributions for Experimentalists[M]. Stockholm: University of Stockholm, 2007: 133-133.

[17] Ramsay C M. The distribution of sums of certain I.I.D Pareto variates[J].-, 2006, 35(1): 395-405. doi: 10.1080/03610920500 476325.

[18] Mathur A and Willett P K. Local SNR consideration in decentralized CFAR detection[J]., 1998, 34(1): 13-22. doi: 10.1109/7.640257.

[19] Donald P B and Nathan A G. Adaptive detection and diversity order in multistatic radar[J]., 2008, 44(4): 1615-1623. doi: 10.1109/TAES.2008.4667736.

Double Threshold CFAR Detection for Multisite Radar

HU Qinzhen SU Hongtao ZHOU Shenghua LIU Ziwei

(,,’710071,)

For multisite radar system, to solve the data transmission rate problem, two kinds of Double Threshold Constant False Alarm Rate (DT-CFAR) detectors, the DT Generalized Likelihood Ratio Test (DT-GLRT) detector and the DT Adaptive Matched Filter (DT-AMF) detector, are proposed based on the GLRT and the AMF algorithms. Fisrt, the local test statistics which exceed the first threshold are transferred to the fusion center. Then, the global test statistic is obtained from the local test statistics and the final decision is made compared to the second threshold in the fusion center. The closed form expression for probabilities of false alarm and detection of the DT-AMF detector are also given when the Signal to Clutter plus Noise Ratios (SCNRs) are identical in the spatial diversity channels. Simulation results illustrate that the DT-CFAR detectors can maintain a good performance with a low communication rate.

Radar; Double hreshold detection; Constant False Alarm Rate (CFAR); Generalized Likelihood Ratio Test (GLRT); Adaptive Matched Filter (AMF)

TN957.51

A

1009-5896(2016)10-2430-07

10.11999/JEIT151163

2015-10-21；改回日期：2016-07-08；网络出版：2016-08-26

苏洪涛 suht@xidian.edu.cn

国家自然科学基金(61372134, 61401329)

The National Natural Science Foundation of China (61372134, 61401329)

胡勤振： 男，1988年生，博士生，研究方向为雷达目标检测及统计信号处理.

苏洪涛： 男，1974年生，教授，研究方向为自适应信号处理、超视距雷达信号处理.

周生华： 男，1982年生，副教授，研究方向为多基地雷达系统及统计信号处理.