软开关隔离型升压DC-DC变换器设计与实现*
2016-10-13茹金平陈得友
茹金平,陈得友
(1.郑州财经学院艺术设计系,郑州450044;2.郑州财经学院计算机系,郑州450044)
软开关隔离型升压DC-DC变换器设计与实现*
茹金平1*,陈得友2
(1.郑州财经学院艺术设计系,郑州450044;2.郑州财经学院计算机系,郑州450044)
为了满足升压型变换器低成本和大功率密度的需求,提出了一种软开关单极隔离型DC-DC变换器。该变换器电路包含一个无损耗缓冲器,通过漏电感固定住开关的电压峰值,从而实现开关的ZVS关断。在失谐状态下,使用Lr-Cr串联谐振电路来实现二极管的ZCS关断。由于磁化电流低,相较于传统的基于反激的变换器,变压器的容量更少。在输出功率250 W和开关频率100 kHz的条件下进行了实际测试,提出的变换器的最大测量效率为97%。
升压型DC-DC变换器;单极开关;软开关;隔离型
隔离型升压DC-DC变换器的应用需求正在逐渐增大,如光伏系统、便携式燃料电池系统以及车载逆变器等。这些应用需求通常要求具有高效率、大功率密度以及低成本[1-2]的性能。
由于输入电流纹波较小,二极管的额定电压较低并且变压器匝数比较小,电流型隔离式变换器更适合升压型应用需求[3]。电流型隔离式变换器有两种类型:无源钳位变换器[4]和有源钳位变换器[5]。无源钳位变换器的结构简单、开关数量少,但是功率损耗过多,这些损耗是RCD缓冲器消耗的并且与主开关的硬开关有关。基于3个基本拓扑结构开发了有源钳位变换器:推挽、全桥和半桥[6-7]。它们不仅实现了因变压器漏感引起的电压峰值的无损耗钳位,还实现了开关的零电压开关(ZVS)开通。然而,由于它们至少需要4个开关和门驱动电路,在高功率和低功率需求下实现成本均较高。
文献[8]提出了适用于功率低应用需求的带有较少开关的隔离式变换器。例如带有一个主开关和一个前卫钳位型开关的隔离式DC-DC变换器实现了开关的ZVS开通,但是关闭了带有硬切换功能的开关[9]。隔离式单极开关DC-DC变换器实现了低成本,因此更具吸引力[10]。Z-源变换器[11]以及反激式变换器[12]在开通和关断的瞬间都采用硬开关。频率控制的反激式变换器以及串联的正-反激式变换器实现了开关的零电流开关(ZCS)开通,但是在关断的瞬间,开关是硬开关。上述单极开关技术增加了变压器的容量,原因在于磁化电感器用于能量转移。隔离式单极开关谐振变换器同时实现了开关的ZCS开通和ZCS关断,但是,对于升压型应用需求,需要具有高变压器匝数比,原因在于电压增益低,因此,此变换器不适合升压型应用需求。
因此,本文提出了一种满足升压应用需求的软开关单极隔离型DC-DC变换器。提出的变换器具有以下特性:(1)不管电压和负载出现任何变化,都会实现开关的ZCS开通和ZVS关断;(2)都会实现所有二极管的ZCS关断,这样可忽略不计与二极管反向恢复有关的电压浪涌;(3)由于CCM操作,输入电流纹波都会较小;(4)由于磁化电流低,变压器的容量都会减少;(5)无损耗缓冲器的额定低,这样可以实现适合升压型应用需求的高效率和低成本。经过100 kHz且250 W的实验测试,结果显示提出的变换器性能满足了设计理念。
1 本文提出的变换器
图1为本文提出的变换器的电路图。
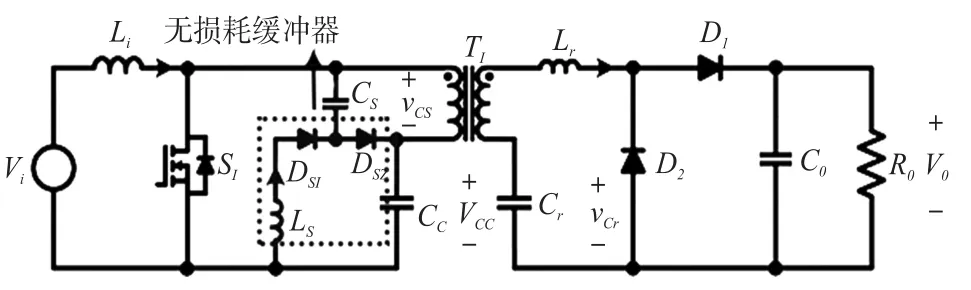
图1 本文提出的隔离式单极开关ZCS-ZVS变换器
本文提出的变换器包括滤波电感器Li、开关S1、包含电容器Cs和电感器Ls的无损耗缓冲器、二极管Ds1和Ds2、钳位电容器Cc以及Lr-Cr串联谐振电路、二极管D1和D2。无损耗缓冲器可以通过漏电感固定住开关的电压峰值,还可以实现开关的ZVS关断。此外,Lr-Cr串联谐振电路可以实现二极管的ZCS关断。图2表示根据谐振频率fi1变化得出的3个谐振操作,谐振频率fi1如式(1)所示:高于谐振的情况(DTs<0.5Tr1)、谐振情况(DTs=0.5Tr1)以及低于谐振的情况(DTs>0.5Tr1)。
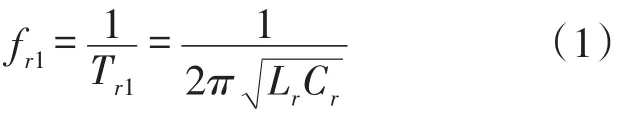
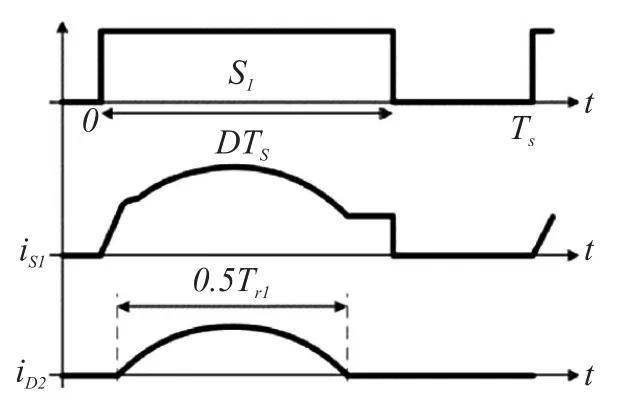
图2 fr1低于谐振(DTs>0.5Tr1)时,对开关及二极管电流波形
从图2中可看出,在低于谐振的情况下,总开关损耗更少。原因在于相较于在高于谐振的情况,在这种情况下,开关关断的电流以及二极管di/dt更小。因此,对于本文提出的变换器,应选择低于谐振的情况,即失谐状态下。
1.1操作模式
图3表示本文提出的变换器的关键波形。为了简化稳态操作时的分析,我们假设输入滤波器和磁化电感足够大,这样在切换周期内会被当作恒流源。同时又假设钳位和输出电容足够大,这样在切换周期内会被当作恒流源。通过钳位式电容器的电压VCc与输入电压Vi一样。在低于谐振的操作下,Ts内有9种模式:
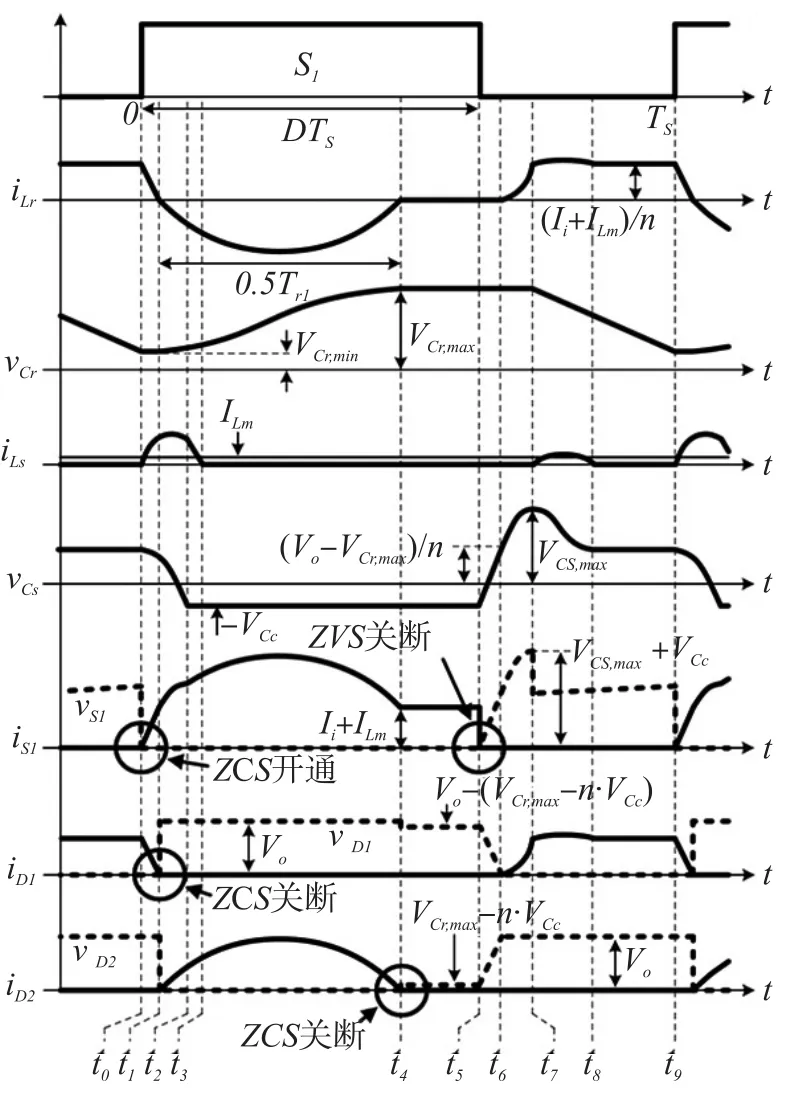
图3 在低于谐振的情况下,本文提出的变换器的关键波形
模式1(t0~t1)当开关S1开通时,开始此模式。图4(a)表示此模式的等效电路。Ls和Cs开始谐振,并且谐振电流iLs通过Ls、Ds1、Cs和S1流动。分别确定了谐振部件的电压和电流,如下所示:
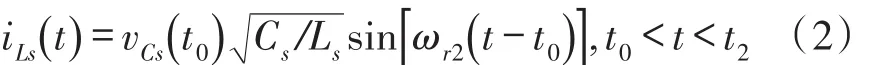
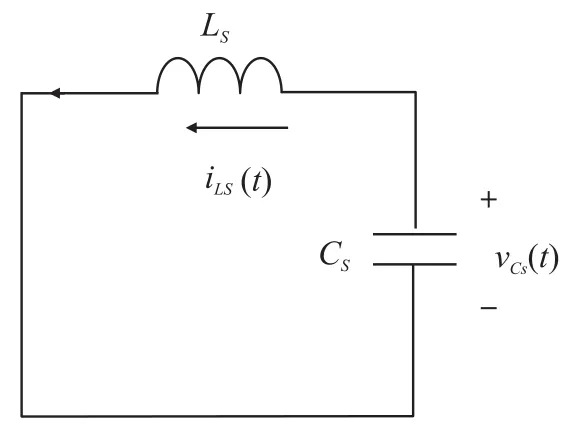
图4(a) 等效谐振电路模式1~2(t0-t1)
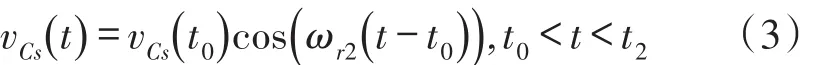
模式2(t1~t2)当电流iLr改变方向时,此模式开始。图4(b)表示此模式的等效电路。Lr和Cr开始谐振,并且谐振电流iLr通过Lr、Cr和D2流动。分别确定了谐振部件的电压和电流,如下所示:
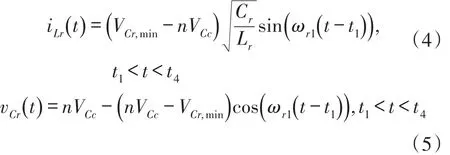
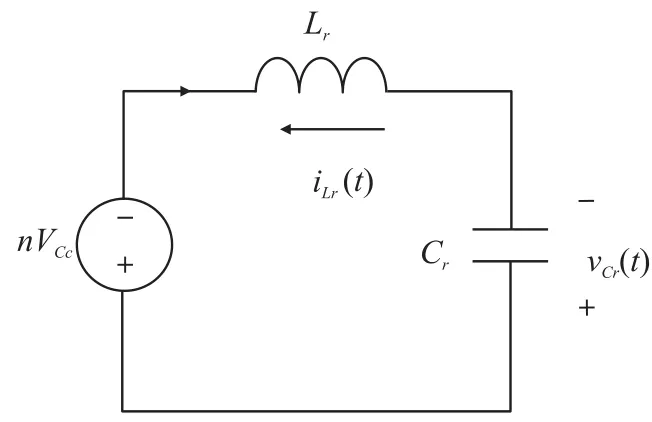
图4(b) 等效谐振电路模式2~4(t1-t4)
模式3(t2~t3)当开通二极管Ds2时,此模式开始。由下列方程确定电流iLs,并且当电流iLs达到0A时,此模式结束。值得注意的是,在ZCS条件下,关断二极管Ds1和Ds2。
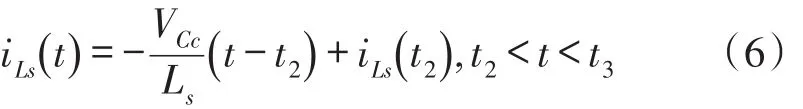
模式4(t3~t4)在此模式期间,Lr-Cr谐振继续进行;当电流iLr达到0 A时,此模式结束。注意:在ZCS条件下,关断二极管D2。
模式5(t4~t5)在此模式期间,恒定电流通过S1流动,此电流的值是输入电流Ii和磁化电流ILm的总和。
模式6(t5~t6)当关断S1时,此模式开始。然后,Ii+ILm通过Cs、Ds2和Cc流动。随着(Ii+ILm)/Cs的斜率增加,下列方程确定的通过缓冲电容器Cs的电压也线性增加,这样出现了S1的ZVS关断。
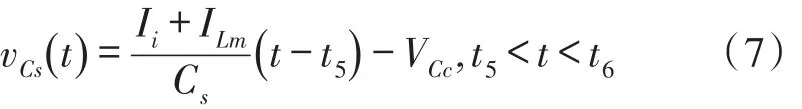
当vCs等于(Vo-VCr,max)/n时,此模式结束。
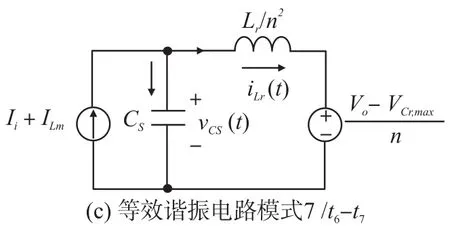
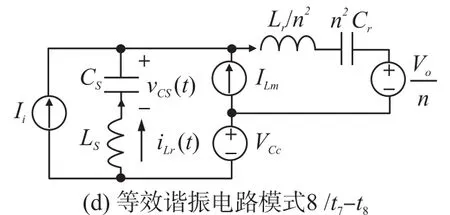
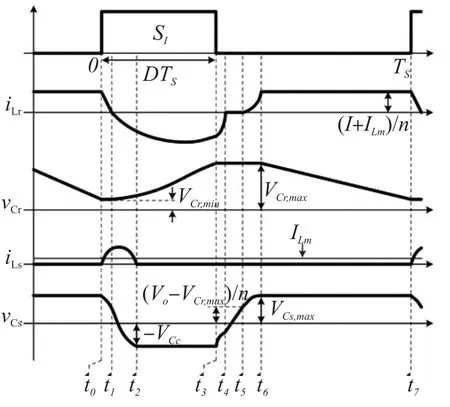
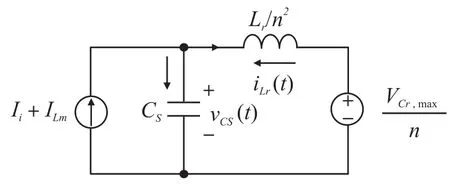
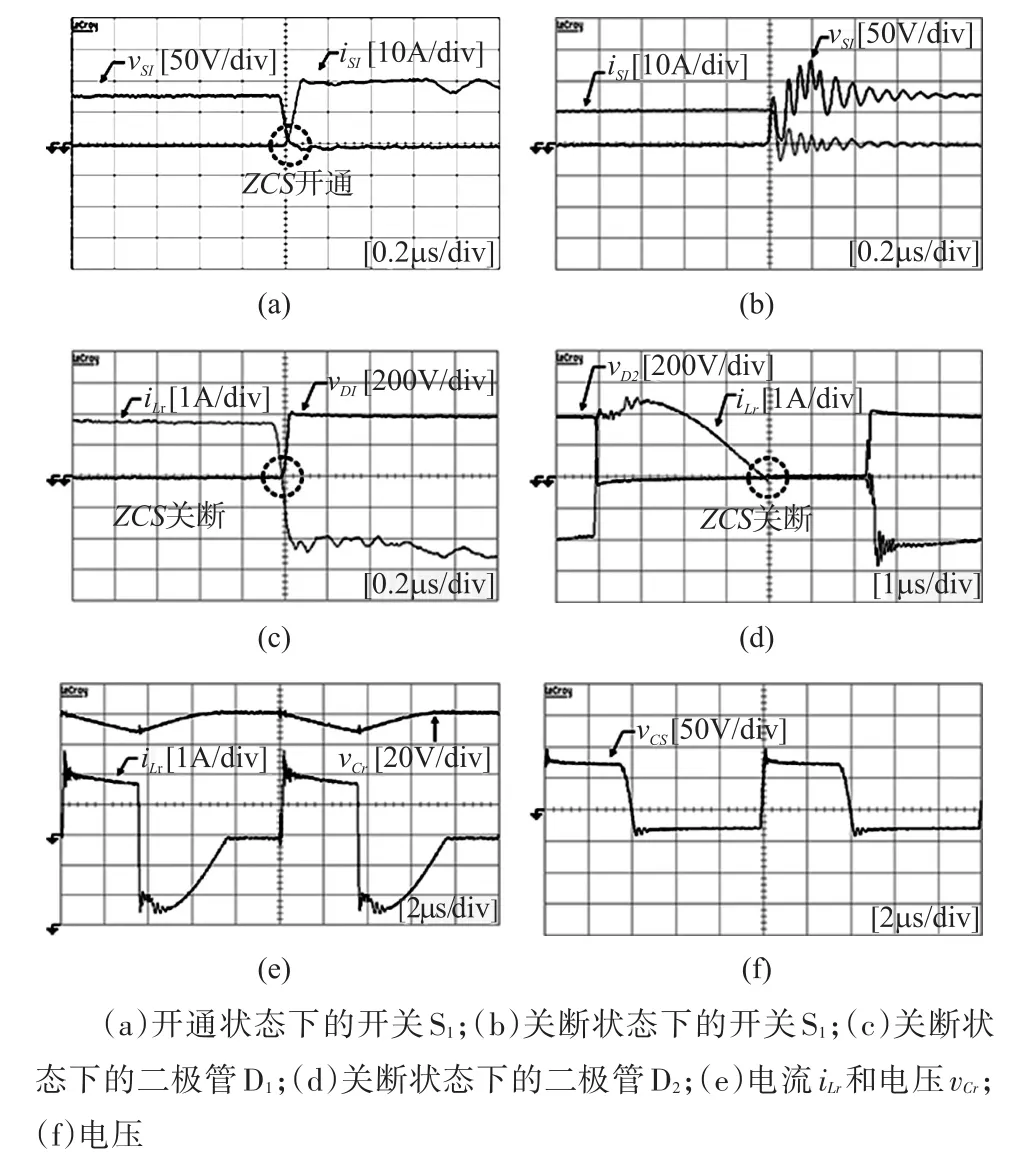
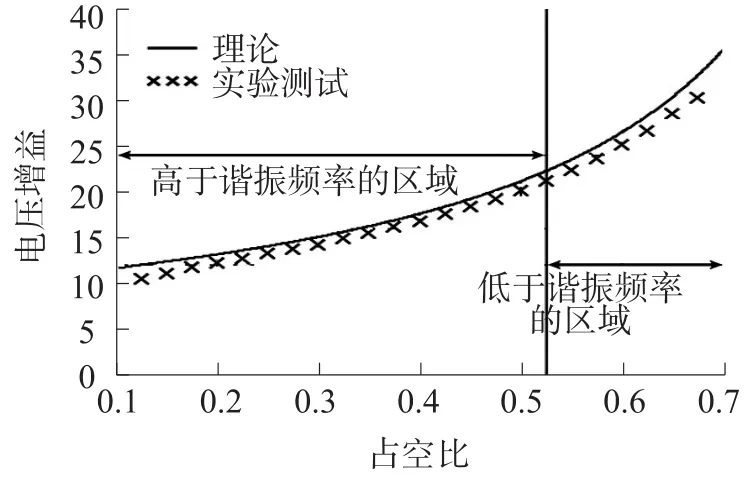
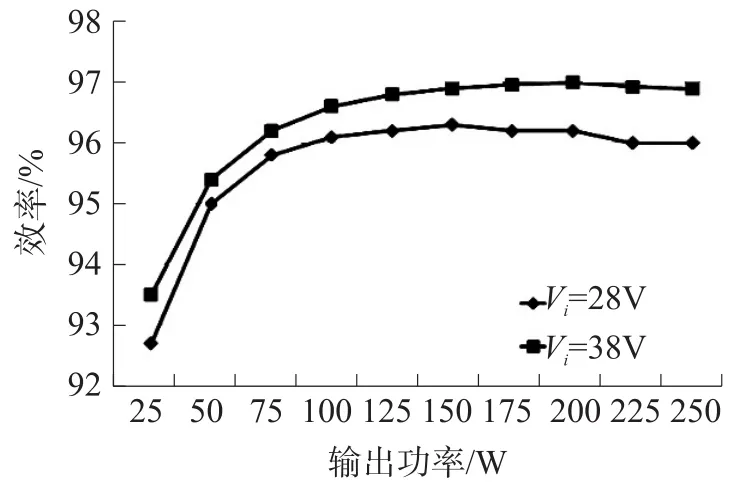
模式7(t6~t7)当开通二极管D1时,此模式开始。图4(c)表示此模式的等效电路。Lr和Cs开始谐振,并且谐振电流通过Cs、Ds2、Lr、D1和Cr流动。我们假设Cs< 图4(c) 等效谐振电路模式7(t6-t7) 模式8(t7~t8)当开通二极管Ds1时,此模式开始。图4(d)表示此模式的等效电路。Ls、Cs、Lr和Cr开始谐振,并且谐振电流iLr通过Ls、Ds1、Cs、Cc、Lr和Cr流动。我们假设Cs< 图4(d) 等效谐振电路模式8(t7-t8) 我们假设在此模式期间iLr≈(Ii+ILm)/n,由下列方程确定电压vCr: 当电流iLs达到0 A时,此模式结束。 模式9(t8~t9)开关S1处于关断状态,输入电流和磁化电流的总和转移到次级。电流iD1等于(Ii+ ILm)/n。当开通开关S1时,此模式结束。 磁化电感器Lm的平均电流等于缓冲电感器Ls的平均电流,原因在于ILs,avg=IDs2,avg和IDs2,avg=ILm,avg。因此,值得注意的是,相较于基于反激的变换器,本文提出的变换器的变压器铁芯容量非常小,原因在于将ILs,av(g=ILm,avg)设计的较小。 1.2电压增益推导 为了获得本文提出的变换器的电压增益,我们假设通过Cc的电压是恒定的,并且在切换周期Ts内可忽略磁化电流。 (1)低于谐振的操作(DTs>0.5Tr1):由于二极管D2的平均电流与稳态下的平均负载电流一样,可获得下列方程: 从式(4)和式(13)可知,由下列方程可获得谐振电容器的最小电压VCr,min: 从式(5)和式(14)可知,由下列方程可获得谐振电容器的最大电压VCr,max: 从式(12)和式(15)可知,由下列方程可获得图3中t7~t9的时间间隔: 从式(7)可知,由下列方程可看出图3中t5~t6的时间间隔: 图3中t6~t7的时间间隔是Lr-Cs谐振频率的四分之一,并且由下列方程确定。 通过将式(16)~式(18)应用到(1-D)Ts,由下列方程可获得电压增益: 其中,A=πfs/2ωr3并且B=Cs(2CrfsRo-1)/2nCr。 (2)高于谐振的操作(DTs<0.5Tr1):图5表示在高于谐振的操作下,本文提出的变换器的关键波形。除了t3~t4的时间间隔,高于谐振的操作原理与低于谐振的操作原理一样。我们假设Cs< 图5 在高于谐振的情况下,本文提出的变换器的关键波形 图6 在高于谐振的条件下t3~t4时间间隔内的等效谐振电路 从式(4)和式(20)可知,由下列方程可获得谐振电容器的最小电压VCr,min: 从式(5)和式(21)可知,由下列方程可获得谐振电容器的最大电压VCr,max: 从式(12)和式(22)可知,由下列方程可获得图5中t6~t7的时间间隔: 我们假设在图5中t3~t5的时间间隔内dvCs/dt≈Ii/ Cs,从式(7)可知,由下列方程可获得时间间隔: 图5中t5~t6的时间间隔是Lr-Cs谐振频率的四分之一,并且由下列方程确定。 通过将式(23)~式(25)应用到(1-D)Ts,由下列方程可获得电压增益: 提出的变换器的设计规格如下所示:输出功率Po=250 W,输出电压Vo=380,输入电压Vi=28 V~38 V,并且开关频率fs=100 kHz。 (1)选择缓冲电感器电流的平均值ILs,avg:为了使缓冲器部件的传导损耗和磁化电流的数量级减到最少,ILs,avg应尽可能的小。从式(2)和式(10)可知,ILs,avg与缓冲电容Cs成正比。然而,如果选择较小的Cs以便减少缓冲器部件的传导损耗,开关的额定电压就会增加,如式(9)所示,会导致开关的传导损耗大。因此,考虑到对开关和缓冲器部件之间的传导损耗进行折衷,选择约为平均输入电流3%的ILs,avg,可表示为: (2)确定n、Lr和Cr的数值:为了简化设计步骤,电压增益可近似于: 如上文所述,由于开关关断的电流和二极管di/dt较小,为本文提出的变换器选择了低于谐振的频率。从图2可知,由下列方程可获得失谐状态下,最小工作周期: 由于应把谐振电感Lr设计为将二极管D1的反向恢复影响降到最小,图3中t0~t1的时间间隔应比3trr1大,可表示为: 其中,trr1是二极管D1的反向恢复时间。 基于前面分析的操作原理,可分别获得开关S1的RMS电流和开通电压,如下所示: 图7表示基于带有不同n值的开关S1的RMS电流和开通电压。在此实际制作中,考虑到对开关S1的传导损耗和开关损耗进行的折衷,选择的变压器n的匝数比为5。通过使用式(28)~式(30),分别由5 μH和560 nF确定谐振值Lr和Cr。 图7 带有不同n值的开关S1的RMS电流和开通电压 (3)确定Cs的数值:通过使用式(2)、式(6)和式(10),由下列方程可获得ILs,avg为: 其中, 通过将n、Lr、Cr和式(27)代入到式(33),缓冲电容Cs可计算为16nF。 (4)确定Ls的数值:应把缓冲电感Ls设计为将缓冲二极管Ds1和Ds2的反向恢复影响降到最低。因此,图3中t2~t3的时间间隔应比3trr2大,可表示为: 其中,trr2是二极管Ds1和Ds2的反向恢复时间。根据式(34),缓冲电感Ls可计算为5 μH。 (5)选择半导体器件:根据之前的设计步骤和操作原理,对本文提出的变换器的半导体器件进行选择。从图3可看出,输出二极管D1和D2有Vo的最大电压应力。从公式(13)可知,输出二极管D2的峰值电流为0.5πIo/Dmin。由下列方程确定通过开关S1的最大电压应力: 由式(31)确定开关S1的电流应力。如图3所示,通过缓冲二极管Ds1和Ds2的最大电压应力分别为vCs(t0)+VCc和VCc。缓冲二极管Ds1和Ds2的峰值电流分别为式(2)中的和Ii。根据之前设计的部件参数值如表1所示。 表1 部件参数值 设计并制作了本文提出的变换器250 W的变换器,并且对其进行测试用以核实本文提出的理念。表1列出了本文提出的变换器的部件参数。我们从表1可看出,缓冲器部件的额定电流远低于主要部件的额定电流。变压器的漏电感作为谐振电感。图8和图9表示当输入电压为28 V时,分别在满载和半载条件下的实验波形。图8(a)和图9 (a)表示在满载和半载条件下,开通带有ZCS的开关S1。图8(b)和图9(b)表示在关断状态下S1的实验波形。然而,从图8(b)和图9(b)可看出,由于原型电路上MOSFET的输出电容和寄生电感之间的寄生谐振造成了振铃,S1产生了少量的损耗。使用专业的生产技术可以减少此损耗。 图8 在Vi=28 V和Po=250 W条件下的实验波形 图9在Vi=28 V和Po=150 W条件下的实验波形: 图8(c)和图9(c)表示在两种条件下,关断带有ZCS的二极管D1。图8(d)和图9(d)表示在两种条件下,关断带有ZCS的二极管D2。图8(e)和图9(e)表示iLr和vCr的波形,与图3中分析的波形较为吻合。在两种条件下,测量的电压VCr,max分别为143.1 V和142.5 V。这与从式(14)和式(15)获得的分析数据(145.8 V和143 V)非常接近。图8 (f)和图9(f)表示vCs的波形。 图10表示在Vi=28 V且Ro=577 Ω的条件下,本文提出的变换器的理论电压增益和实验电压增益。实验的电压增益与理论电压增益较为吻合。 图10 在Vi=28 V且Ro=577 Ω的条件下,本文提出的变换器的理论电压增益和实验电压增益 对本文提出的变换器的效率进行测量,如图11所示。当输入电压为38 V时,在250 W的条件下,本文提出的变换器的最大测量效率为97.0%。根据输入电压出现的变化,在Vi=28 V条件下的测量满载效率为96.0%;在Vi=38 V条件下的测量满载效率为96.9%。图12表示本文提出的变换器实物图。 图11 本文提出的变换器的测量效率 图12 本文提出的变换器实物图 为了满足光伏系统、便携式燃料电池系统及车辆逆变器等升压型DC变换应用的需求,本文提出了一种软开关单极开关隔离式变换器。相较于传统的基于反激的变换器,本文提出的变换器的实现成本更低且功率密度较大,原因在于其具有改进的特性,如:开关和二极管具有全软开关的特征、无损耗缓冲器的额定较低以及变压器的容量减少。经过100 kHz和250 W的变换器实际测试,得出的实验结果验证了提出的变换器的正确性,且在250 W的条件下,获得了97.0%的最大测量效率。 [1]Ma H,Chen L,Bai Z.An Active-Clamping Current-Fed Push-Pull Converter for Vehicle Inverter Application and Resonance Analy⁃sis[C]//Industrial Electronics(ISIE),2012 IEEE International Symposium on.IEEE,2012:160-165. [2]Choe S Y,Ahn J W,Lee J G,et al.Dynamic Simulator for a PEM Fuel Cell System With a PWM DC/DC Converter[J].Energy Con⁃version IEEE Transactions on,2008,23(2):669-680. [3]Nymand M,Andersen M A E.High-Efficiency Isolated Boost DCDC Converter for High-Power Low-Voltage Fuel-Cell Applica⁃tions[J]IEEE Trans Ind Electron,2010,57(2):505-514. [4]Park K B,Moon G W,Youn M J.Two-Transformer Current-Fed Converter with a Simple Auxiliary Circuit for A Wide Duty Range [J].Power Electronics IEEE Transactions on,2011,26(7):1901-1912. [5]Kim H,Yoon C,Choi S.An Improved Current-Fed Zvs Isolated Boost Converter For Fuel Cell Applications[J].Power Electronics IEEE Transactions on,2010,25(9):2357-2364. [6]褚恩辉,叶树仁,王遨宇.一种新型的有源软开关变换器[J].电机与控制学报,2011,15(5):72-77. [7]张云安,孙强,王阳.峰值电流模式的移相半桥三电平DC/DC变换器闭环系统建模研究[J].电子器件,2008,31(6):1828-1831. [8]York B,Yu W,Lai J S.Hybrid-Frequency Modulation for PWMIntegrated Resonant Converters[J].IEEE Transactions on Power Electronics,2013,28(2):985-994. [9]张相军,刘冠男,王懿杰,等.软开关双向DC-DC变换器控制模型[J].电机与控制学报,2013,17(11):89-96. [10]魏山力,项安.隔离升压推挽式软开关DC/DC变换器双闭环控制系统设计[J].机电一体化,2014,20(1):42-46. [11]王宇星,朱波.一种用于PWM控制Buck型DC-DC变换器的带隙基准源[J].电子器件,2013,36(2):252-255. [12]Lee J H,Liang T J,Chen J F.Isolated Coupled-Inductor-Integrat⁃ed DC-DC Converter with Nondissipative Snubber for Solar Ener⁃gy Applications[J].Industrial Electronics IEEE Transactions on,2014,61(7):3337-3348. 茹金平(1980-),女,汉族,黑龙江鹤岗人,大学本科,讲师,主要研究方向为计算机应用、平面设计,rujinping@126.com。 Design and Implementation of the Soft Switching Isolation Boost DC-DC Converter* RU Jinping1*,CHEN Deyou2 In order to meet the demand of low cost and high power density of the boost converter,a soft switching DC-DC converter with unipolar switching mode is presented.The converter circuit contains a non loss buffer,which is fixed by the leakage inductance of the switch voltage peak,thereby achieving the switch of the ZVS off.In the con⁃dition of failure,the Lr-Cr series resonant circuit is used to realize the ZCS off of the diode.Due to the low magneti⁃zation current,the transformer capacity is less than the traditional fly-back converter.Under the condition of the out⁃put power 250 W and the switching frequency 100 kHz,the maximum efficiency of the converter is 97%. boost DC-DC converter;single pole switch;soft switch;isolation type TM46 A 1005-9490(2016)02-0305-07 EEACC:1290B10.3969/j.issn.1005-9490.2016.02.013 项目来源:基于C++技术的学校排课系统设计与实现项目(豫教201413658) 2015-07-30修改日期:2015-08-27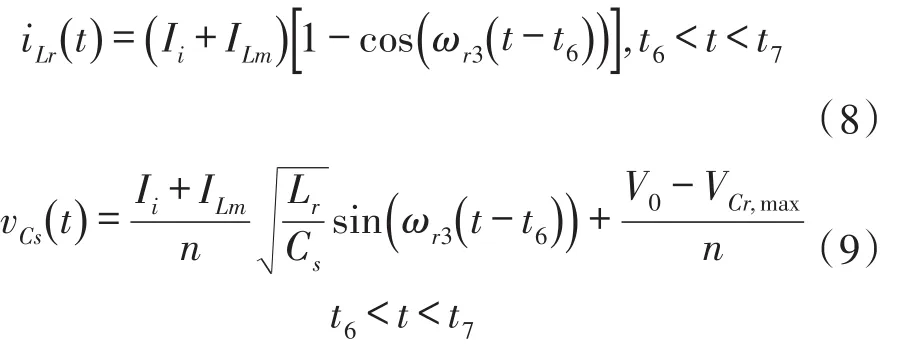
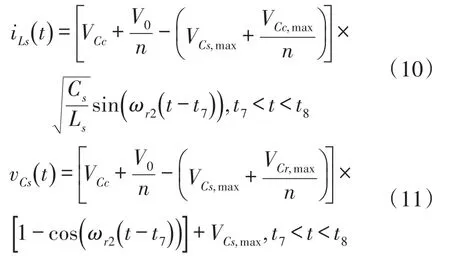
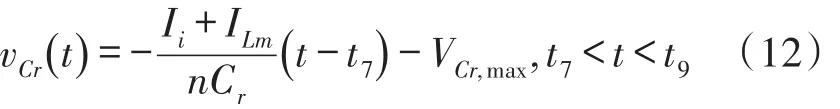
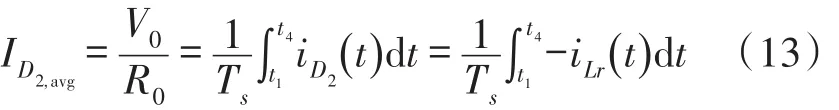
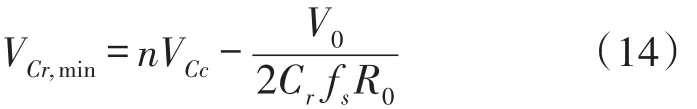
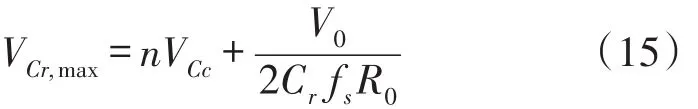

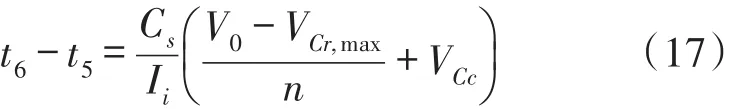


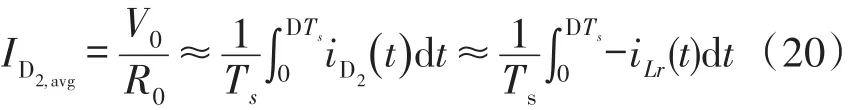
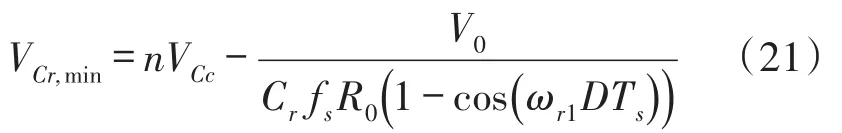
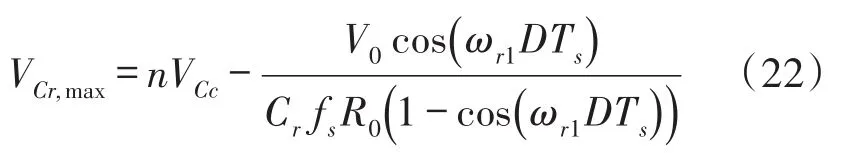

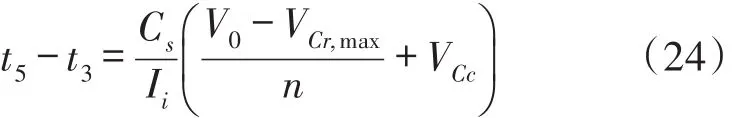


2 具体设计步骤
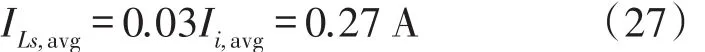


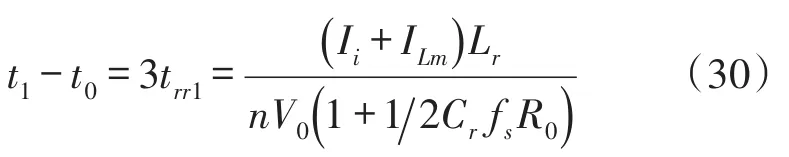
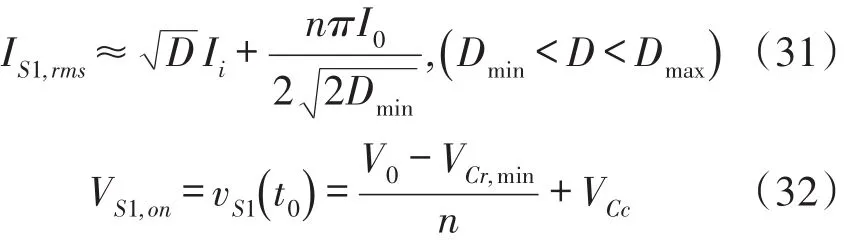
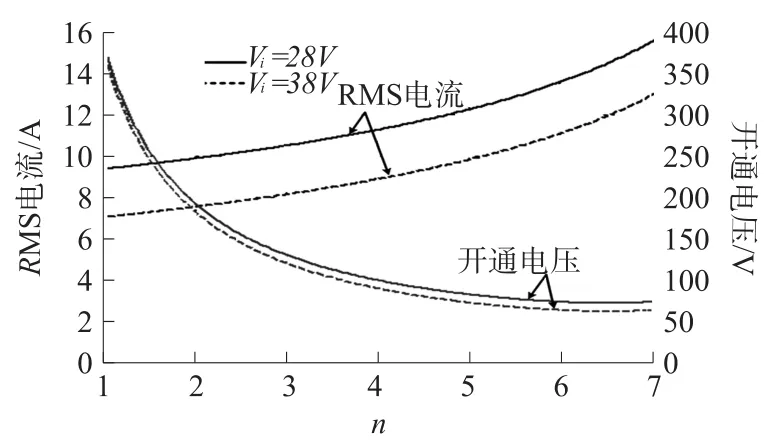
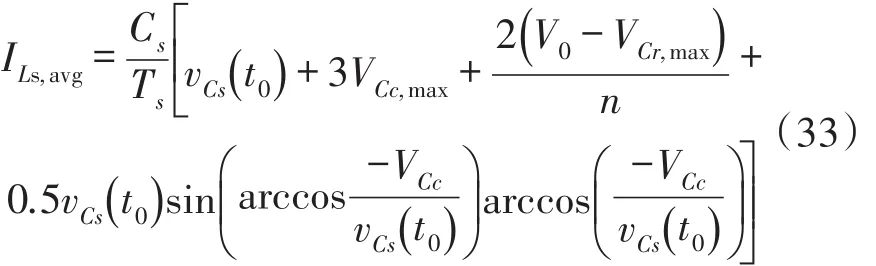
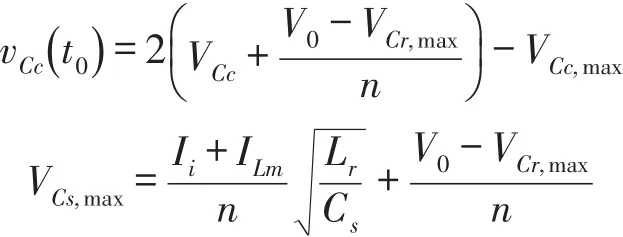
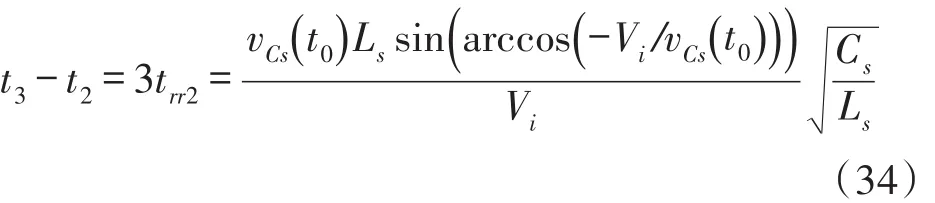
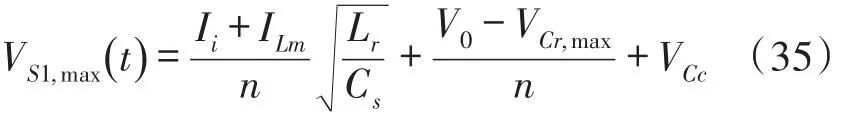

3 实验结果

4 总结

(1.Department of Art Design,Zhengzhou College of Finance and Economics,Zhengzhou 450044,China;2.Department of Computer,Zhengzhou College of Finance and Economics,Zhengzhou 450044,China)
