超磁致伸缩致动器的等效电路研究及驱动波形设计
2016-10-13薛光明张培林何忠波孙也尊李冬伟
薛光明, 张培林, 何忠波, 孙也尊, 李冬伟
(1.军械工程学院车辆与电气工程系,河北石家庄050003;2.总装军代局驻二四七厂军代室,山西太原030009)
超磁致伸缩致动器的等效电路研究及驱动波形设计
薛光明1, 张培林1, 何忠波1, 孙也尊2, 李冬伟1
(1.军械工程学院车辆与电气工程系,河北石家庄050003;2.总装军代局驻二四七厂军代室,山西太原030009)
针对超磁致伸缩致动器由于大电感线圈的存在而使电流上升时间较长,以致于无法满足快速开启需求的问题,分析了致动器等效电路以计算精确的线圈电流,并设计了较为合理的驱动电压波形。从对致动器阻抗的描述精度出发考察3种等效电路,确定了带并联电阻的等效形式最为合理;分析计算了该种等效形式下方波电流输入时的电流表达式,得到不同频率下致动器电流瞬时响应,并通过实验测试了致动器阻抗以及电流瞬时值以验证等效电路的准确性。最后基于该等效电路,借鉴电磁阀的大电压开启方法,分析了合理的电压形式并提出了参数设计方案,计算结果表明,设计电压能在保证较小超调量的同时有效地降低电流调整时间。
超磁致伸缩致动器;等效电路;阻抗;瞬态响应;驱动电压
0 引言
超磁致伸缩材料(giant magnetostrictive material,GMM)是一种较为新型的功能材料,具有磁致伸缩应变大、磁机耦合系数高、响应速度快及居里点温度高等优良性能[1-3],在减振降噪、力或位移检测、超精密加工及流体器件设计等方面有着广泛应用[4-7]。超磁致伸缩致动器(giant magnetostrictive actuator,GMA)是超磁致伸缩材料最常见的应用形式,采用一定的预压机构使超磁致伸缩材料处于良好的输出状态,并通过激磁线圈及偏置磁铁产生的磁场将材料驱动。
超磁致伸缩致动器结构形式确定后,驱动电源对致动器的瞬态和稳态特性有着重要影响,国内外学者对超磁致伸缩致动器的驱动技术进行了一定研究。大连理工大学的杨兴等[8]基于功率MOSFET元件设计了线性度高、误差小且响应速度快的驱动电源;浙江大学的葛荣杰等[9]利用连续调整型恒流源原理设计了大功率恒流源,可实现电流在-3~+3A范围内连续可调;德克萨斯农机大学的Won-jong Kim等[10]借助有限元技术对超磁致伸缩致动器线圈进行改进,并设计了三相电源的局部激励方案,减小了致动器功率损耗;长安大学的王松等[11]基于DSP主控芯片设计了带控制电路的驱动电源,实现SPWM波形的输出,并具有过流保护及谐振频率自动跟踪的功能;山东大学的李永等[12]基于PWM逆变器设计了驱动电源,并建立了驱动模型。
以上电源设计从致动器的稳态电流幅值出发,并重点研究了电路器件设计,取得了较好的效果,然而对致动器输出的瞬态过程以及致动器适用的理想电信号形式研究较少。实际上,由于大电感线圈的存在,致动器的响应速度并不快。致动器输出需经历电生磁和磁产生机械效应两个过程,由于超磁致伸缩材料的磁机过程非常迅速,整个致动器的响应时间与电生磁的时间大致相等。又由于线圈通入电流的瞬间即产生磁场,致动器响应时间几乎等于线圈两端加压至线圈内电流稳定的时间。线圈电感对电流的上升或下降时间有较大影响,电感越小,响应时间越短,然而超磁致伸缩材料对磁场强度的需求较大,线圈电感的降低会使外磁场强度降低,而使致动器输出位移不够[13-14]。因此,整个致动器的响应速度并不快,甚至不如某些高速电磁铁,这限制了超磁致伸缩材料在对驱动器瞬态特性要求较高场合(如高压共轨喷油器)的应用[15-16]。如何削减线圈电流响应时间,将超磁致伸缩材料的真实输出特性表现出来具有重要的研究价值。
本文着眼于超磁致伸缩致动器的瞬态性能提升,对比确定了较合理的致动器电路等效方案,并从稳态特性和瞬态特性两个角度验证等效电路的准确性,继而基于此等效电路对线圈电流进行分析,借鉴电磁式驱动器中的大电压驱动主喷射脉宽,计算了适用于超磁致伸缩致动器的理想驱动方波。研究内容具有较强的适用性,且对致动器部件的优化以及驱动电源的电路设计具有一定指导意义。
1 喷油器用超磁致伸缩致动器
现行高压共轨喷油器多采用常闭式球阀,断电时球阀关闭,通电后再打开,对应在驱动器上为断电时尺寸最长,通电后缩短。由于超磁致伸缩材料在通电后总是伸长的,需采用一定的措施将此伸长转化为致动器尺寸的缩短,如施加强偏置磁场、采用筒式材料等。本文设计了一种超磁致伸缩致动器,借助一个筒式杆件可实现位移的有效转化,其具体结构如图1所示。
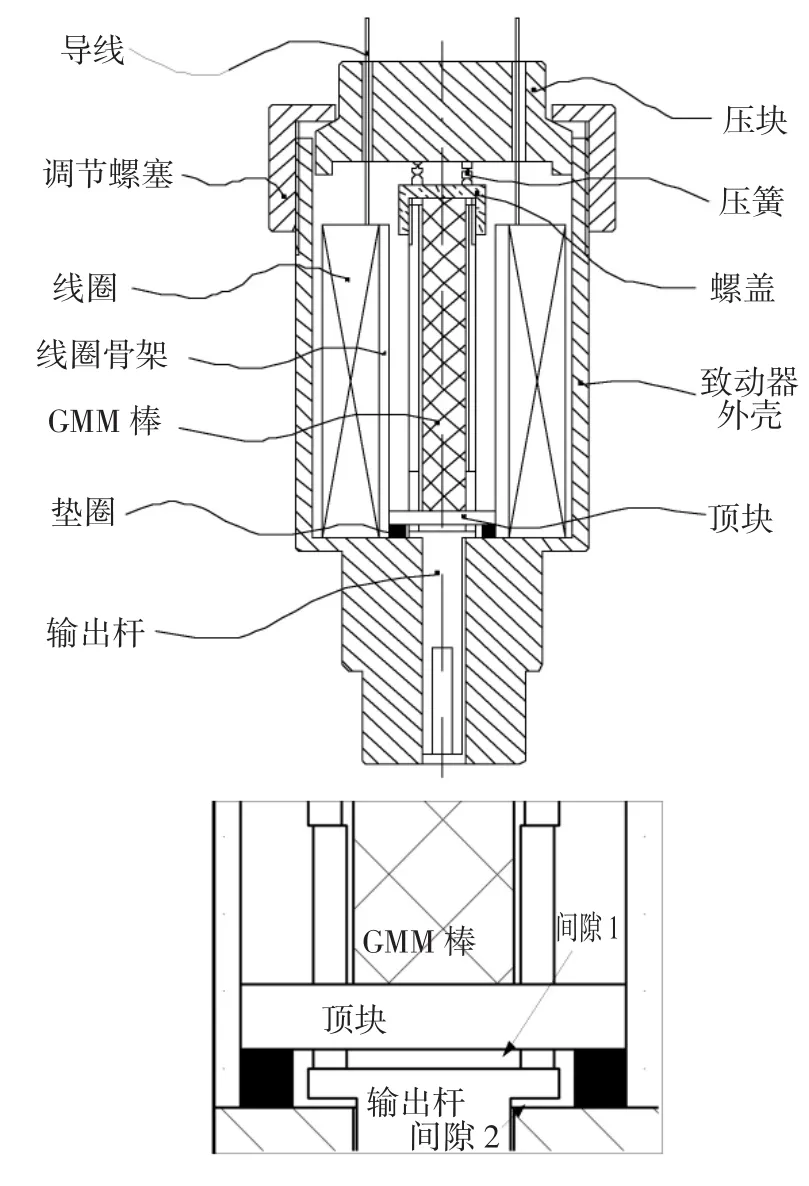
图1 喷油器用超磁致伸缩致动器结构图Fig.1 Diagram of the GMA used on electric injector
2 致动器等效电路
2.13种等效电路
对于1节所设计的超磁致伸缩致动器,研究其线圈中的电流需对整个致动器的电路进行等效。以电感线圈为核心,超磁致伸缩棒可视为线圈的铁心,对线圈电感有一定影响,其它部件对线圈电感也有一定影响。普通空心或铁心线圈常等效为一个无感电阻与理想电感的串联,这种等效方法形式简单,在输入信号频率较低时效果不错,描述电流的瞬态特性也具有一定精确度。然而模型参数较少,对于高频输入或影响因素较多的情形描述精度不够。为此本文对此等效模型进行优化,一个想法是考虑多匝线圈各层之间的并联电容,另一个是引入并联电阻的等效形式,3类等效电路及其参数如图2所示。
下面计算3种等效电路的阻抗。对于图2(a)电路,其等效阻抗Za为

由计算结果可知,Za的相角正切值为ωL/R,该值总是随输入信号的频率的增大而成比例增大,因而该等效电路在刻画相角时具有一定局限性。
对于图2(b)和图2(c)形式的等效电路,二者等效阻抗Zb和Zc分别为
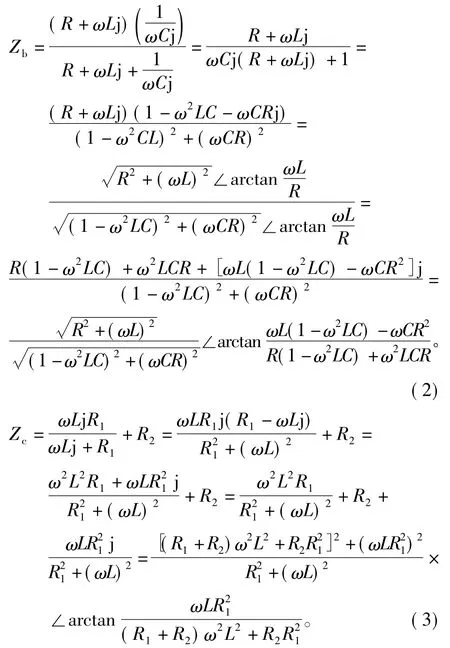
由式(2)和式(3)可知,由于分别增加了一个参量,图2(b)和图2(c)等效方案对阻抗的幅值或相角刻画更加丰富,克服了图2(a)电路的缺陷。
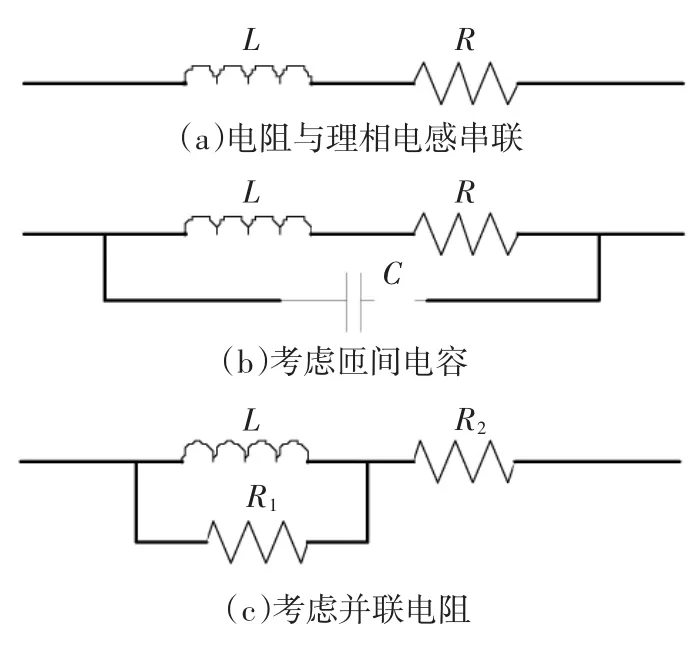
图2 致动器电路的3种等效方式Fig.2 Three kinds of equivalent circuits of the actuator
2.2等效电路参数辨识及对比
下面对3种等效电路中的参数进行分析并对比等效方案的优劣。对于3种等效电路中电阻、电感和电容的大小,直接采用LCR数字电桥的测量结果不够精确,因为电桥测量只针对某几种内置的电路形式,非内置电路器件的测试并不适用;而且等效电路是一种简化形式,直接测试结果考虑其它因素较少,测量值并不是使该种等效方案描述致动器阻抗最理想的等效值。因此这里采用LCR数字电桥测试致动器等效阻抗的模和相角,并根据试验结果对3种等效电路中的参数进行辨识,然后代入辨识参数对比3种方案。
以等效电路的计算阻抗与实测阻抗的相对误差来评定等效结果。相对误差定义为计算与实验结果的差值除以实验结果的比值,首先通过数字电桥测得不同频率下的致动器阻抗的模和相角,分别计算不同频率下的模和相角的相对误差,取这两组相对误差中的最大值P作为评定标准,
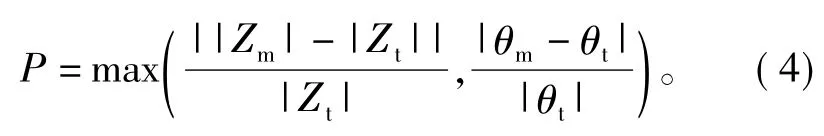
式中:|Z|和θ分别为阻抗的模和相角,下标m、t分别表示等效电路计算和实验结果。采用相对误差最大值能保证等效电路在所有测试频率下,对阻抗模或相角的描述均比较精确,P越小,说明等效电路模型越准确。各等效电路的参数辨识也以P最小化为目标,可以最大限度地发挥各等效模型的性能。
3种等效电路的参数辨识是一个无约束多变量优化问题,其目标为使P取最小值,采用Matlab中的fminsearch函数进行多变量搜索,为减少时间,LCR数字电桥直接测试10 Hz下电阻、电感和电容作为搜索初值。测试的超磁致伸缩致动器图3所示,参数初值、辨识结果以及该等效方案下评定标准最小值Pmin如表1所示。

图3 致动器实物Fig.3 Actual object of the actuator
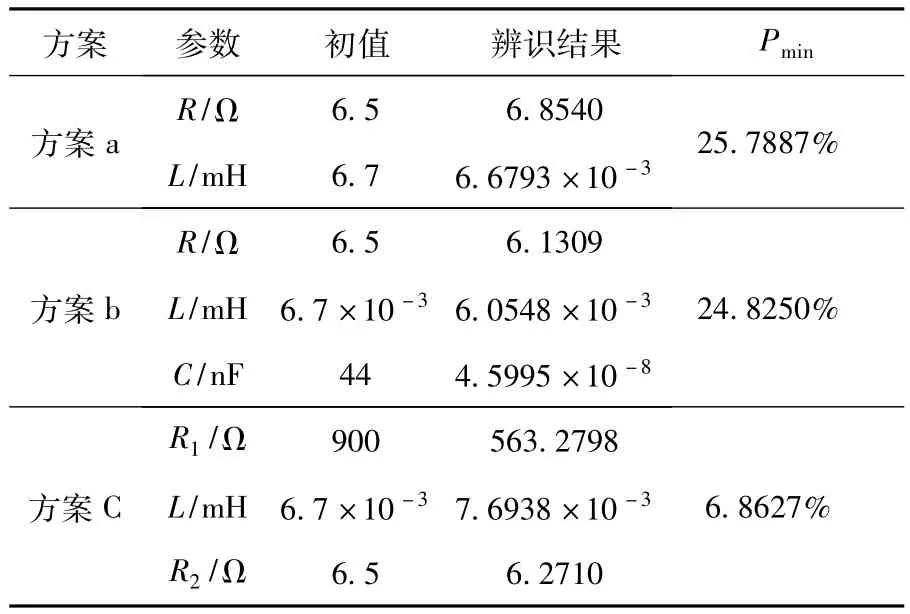
表1 参数计算结果Table 1 Calculated results of parameters
由计算结果可知,前两种方案对不同频率下致动器阻抗的描述精确度较差,某个频率下的最大相对误差超过了20%,而方案c较为准确,所有相对误差均小于7%。为进一步分析3种方案的效果,将辨识结果代入等效模型,得到模和相角的模型计算结果与实验结果分别如图4和图5所示,3种等效的相对误差如图6所示。
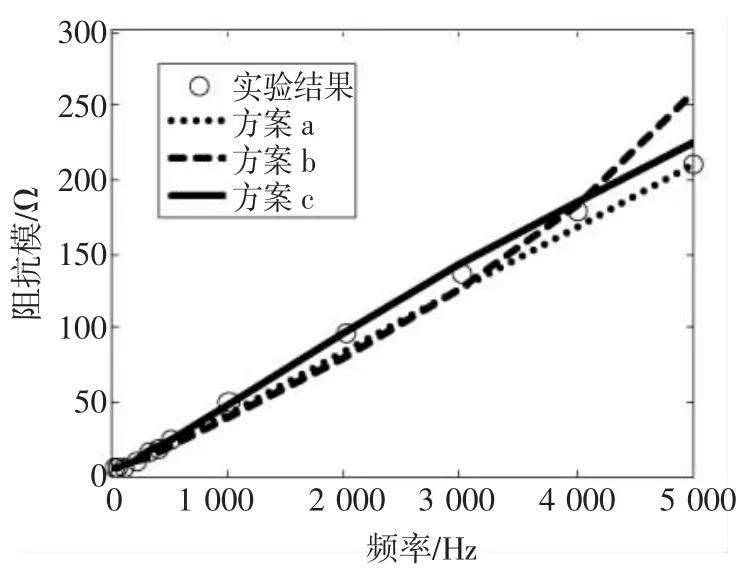
图4 阻抗模的实验与计算结果Fig.4 Experimental and calculated result of the modulus
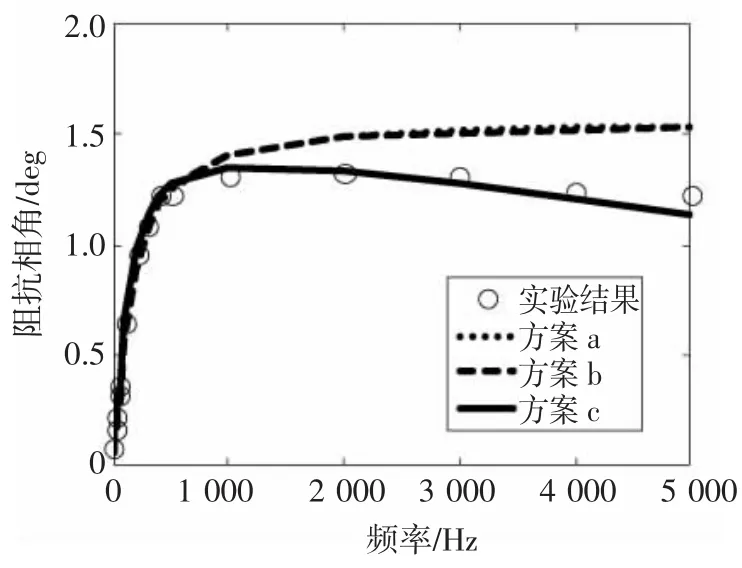
图5 阻抗相角的实验与计算结果Fig.5 Experimental and calculated result of the phase

图6 3种等效阻抗的相对误差Fig.6 Relative error of the three equivalent circuits
分析实验和计算结果可知,采用方案a描述致动器等效阻抗具有一定精确度,但对低频和高频的情况不能同时描述精确,尤其是在计算相角时,Za的虚部随频率的增大而增大(见式(1)),使得计算相角也随频率增大而增大,这与实验结果不符。方案b虽然引入了匝间电容这一变量,但对阻抗的描述改观不大,实际上,方案b在单独描述阻抗模或相角趋势时效果比较理想,也能刻画相角在一定频率后随频率增大反而减小的情况,但不能同时使计算模和相角具有一定精度。对比前两种等效方案,方案c计算精度较高。
由相对误差计算结果可知,方案a描述阻抗相角的效果比较差,且在频率的两端位置相对误差最大,超过了25%;方案b和c对模和相角描述的误差分布大致相当,在频率轴的两端相对误差偏大,但方案c的相对误差整体较小,说明等效方案比较理想。
由以上分析可知,考虑并联电阻形式的致动器等效电路对阻抗的描述比较有效,且适用于不同频率的情况,测试频率点处的相对误差均小于7%,具有较高精度。
3 等效电路瞬态特性分析
3.1瞬态过程计算
以上对带并联电阻等效电路的阻抗进行了分析,阻抗的模决定了谐波激励下的稳态电流幅值,相角决定了电流的滞后相位,因此以上分析相当于是方案c等效电路的稳态特性分析,要验证等效电路的准确性,还需对该电路的瞬态特性进行分析和验证。采用方波输入研究等效电路在通电和断电的暂态过程,如图7所示,其中i(t)为流经线圈的等效电流。
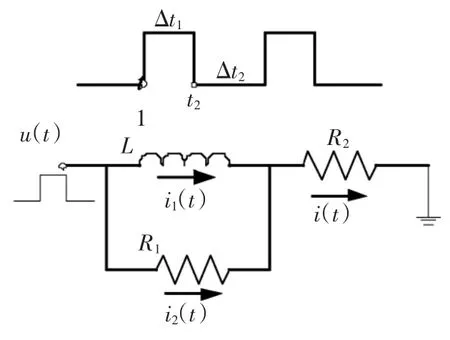
图7 等效电路输入电压及电流Fig.7 Input voltage and energized current of the circuit
由节点电流定律得,流经线圈的电流i(t)为理想电感电流i1(t)和并联电阻电流i2(t)之和,即
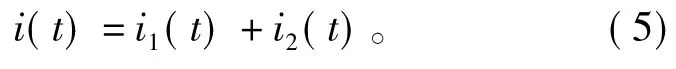
由节点电压定律得,理想电感与并联电阻两端的电压相等
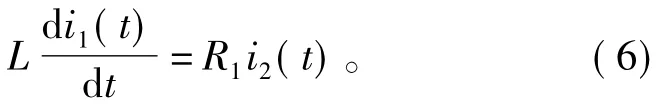
此外,输入电压u(t)为并联电阻和串联电阻的压降和
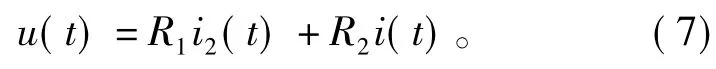
整理式(5)、式(6)和式(7)可得
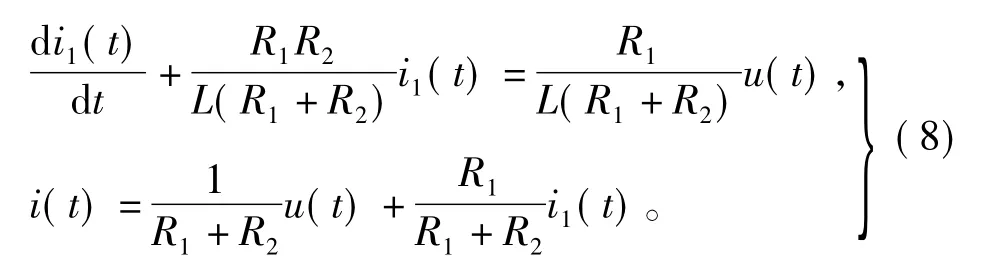
求解时,先求解i1(t),再求解i(t),可以避免多个微分项的计算。通电时,若记方波电压幅值为U,电压上升时刻为 t1,则式中 i1(t)的通解为C1e-(t-t1)/τ+U/R2,代入第2式可得 i(t)通解(C1为任意常数)。设t1时刻电流i(t)初值为Ir0(非i1(t)的初值),代入可得C1,整理即得通电时等效电路中上升电流变化ir(t)规律为
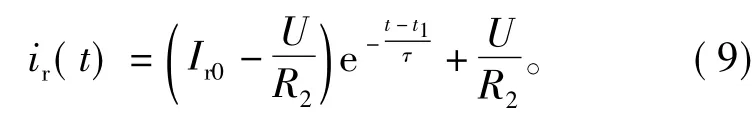
式中τ为时间常数,且τ=L(R1+R2)/R1R2。
断电时,电压幅值为0,记电压下降时刻为t2,式(8)中i1(t)的通解为C2e-(t-t2)/τ,代入第2式可得i(t)通解(C2为任意常数)。设t2时刻电流i(t)初值为Id0,代入可得C2,整理即得断电时等效电路中下降电流变化id(t)规律为

除初始输入方波外,上升电流初值Ir0为上一个方波的下降电流终值,即 Ir0=id(t2+Δt2)= Id0e-Δt2/τ,在图8中的低压持续时间Δt2较大时,下降电流接近为0,Ir0也近似为0。同理,下降电流初值Id0为上升电流终值,即 Id0=ir(t1+Δt1)=Ir0e-Δt1/τ+U/R2(1-e-Δt1/τ),在高电压持续时间 Δt1较大时,上升电流接近稳态值U/R2,Id0也近似为U/R2。
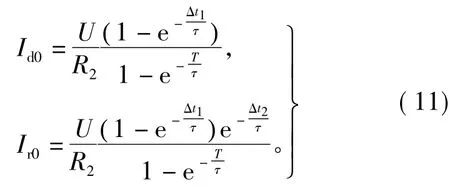
式中,周期T=Δt1+Δt2。
3.2测试及验证
喷油器用超磁致伸缩致动器电压及电流测试系统如图8所示。计算机利用PicoScope 6软件产生数字信号,借助数字示波器(PicoScope 2000)转化为模拟信号,经功率放大器(GF800)放大输入致动器线圈,线圈电流及两端电压由功率放大器监视口输出至数字示波器,最后导入计算机进行采集。

图8 致动器测试系统Fig.8 Testing setup for the actuator
3.1节最后一段对电流初值进行了说明,设定占空比为50%,持续时间Δt1和Δt2较大(电流值趋于稳定)、较小(电流值仍在变化)分别对应方波低频、高频的情况,这里以频率 f分别取 10 Hz、100 Hz、500 Hz为例进行验证。10 Hz时,输入电压幅值U=1.6V,Δt1=Δt2=0.05 s,L、R1、R2为表1中的辨识结果,任一上升沿Ir0≈0,下降沿Id0≈U/ R2(由结果可验证),代入至式(9)和式(10)中可得模型计算结果,与测试结果对比如图9(a)所示。方波频率分别取100 Hz和500 Hz时,采用式(11)确定初值,模型计算结果与测试结果对比分别如图9中(a)和(b)图所示。
由结果可知,基于等效电路的计算结果与实验结果比较吻合,在描述方波电流的上下限、上升及下降时间、电流变化趋势方面具有一定精度,验证了致动器等效电路描述电流瞬态变化的有效性。
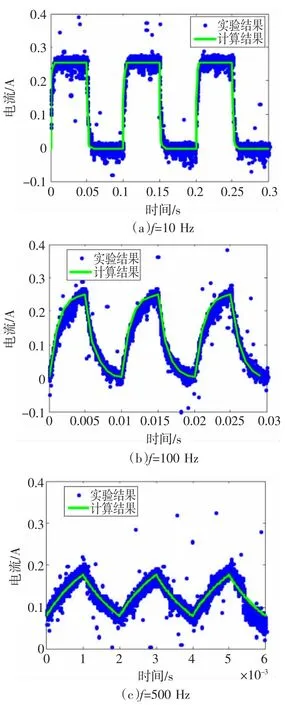
图9 计算与实验结果对比Fig.9 Calculated and experimental results
4 理想驱动电压设计
经过验证,带并联电阻的等效电路在描述致动器阻抗和刻画电流瞬态特性方面具有较高精度,下面基于该模型对致动器的输入电压进行优化。
4.1电压形式分析
由图9中的仿真结果可以看出,由于线圈电感的存在,超磁致伸缩致动器的响应有所延时,为提升响应速度,这里利用电控喷油器电磁阀的大电流开启方法:先用大电压使电流迅速增大,再输入较低电压使电流稳定在一定幅值。超磁致伸缩材料并不能直接采用电磁阀驱动器的高频开关电信号,因为电磁阀的衔铁是被电磁力吸附住的,即使电流在小范围内发生波动,衔铁位置不会发生变化,而超磁致伸缩材料会随电流变化而发生形变,导致致动器位移变化,虽然位移变化在材料磁饱和时影响不大,但会引起不利的油压波动。因此超磁致伸缩致动器的驱动电压仍应采用较低频的方波。
图10为不同电压输入时的电流波形图。普通方波输入时,电流需到稳态才能达到所需幅值,在电感较大时上升时间ton较大。采用图10(b)所示的电压形式输入时,初始输入高电压可使电流迅速增大至所需电流,然后电压立刻降低至维持电压,由式(9)可知初始电流Ir0=U/R2时,电流值将保持为U/R2而不发生变化。这种情况比较理想,然而由于开关器件无法实现电压瞬变,所以设计了图10(c)所示的实际可执行波形。(由于理想喷射形式是“快开慢关”,断电时的电流衰减速度可以较慢。)
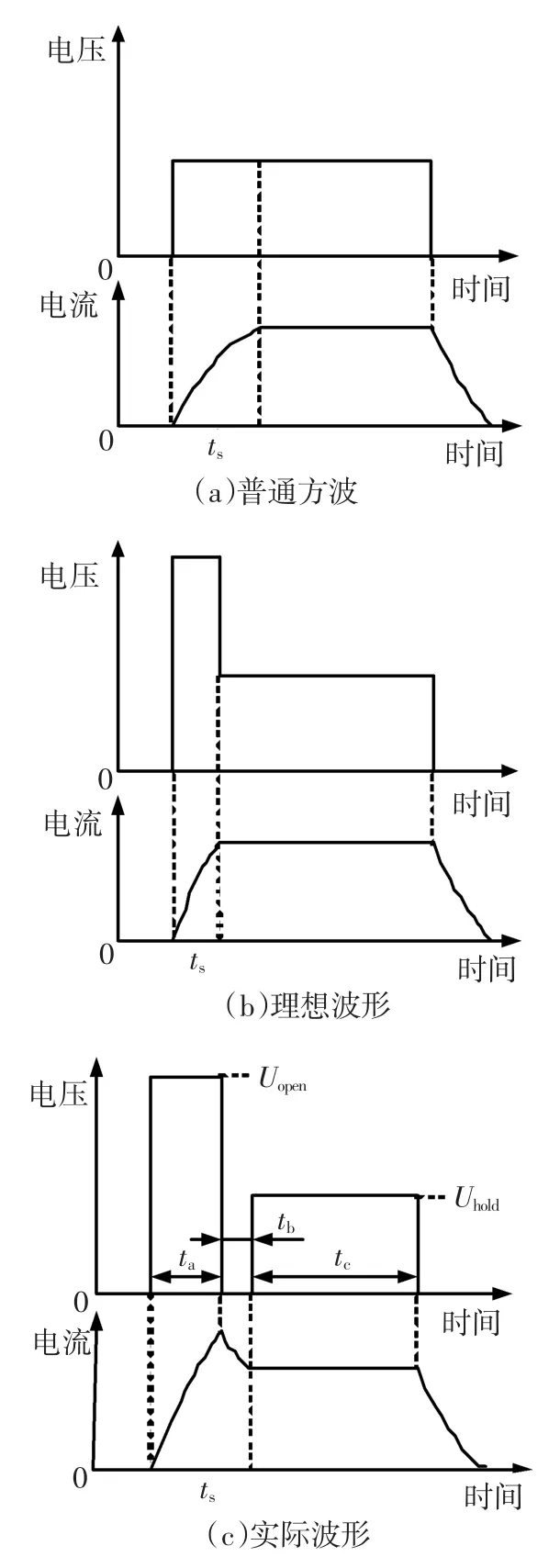
图10 不同输入电压形式及线圈电流Fig.10 Different input voltages and energized currents
实际波形中,先通入较高的开启电压Uopen,持续时间为ta,由式(9)可知,电流将增大至一个较高点-Uopene-ta/τ/R2+Uopen/R2,为减小调整时间,经过断电时间tb,电流应恰能降至所需电流,即
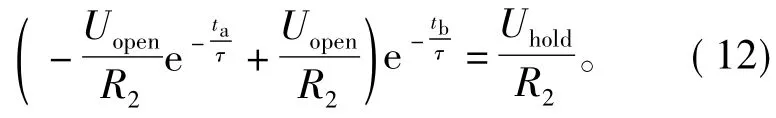
整理上式可得ta和tb的关系
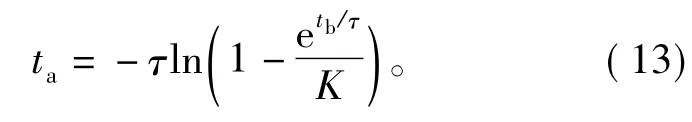
式中:电压比K=Uopen/Uhold>1,而且为保证表达式有意义,设计的驱动波形应满足1-etb/τ/K>0。
又有电流调整时间ts为ta与tb之和,即
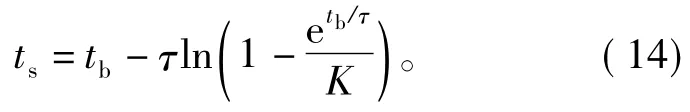
除减小ts外,输入波形应尽量减小电流超调量M,M定义为最大电流值超过稳态值的百分比

根据式(14)和式(15)可得到ts、M与tb之间的关系曲线如图11所示。
由图11可知,tb越小,电流调整时间ts越短,超调量M也越小,对电流迅速稳定是有利的;开启电压Uopen越大(K越大),ts越小,但过大的Uopen容易造成电子器件失效,应在保证电路可靠的情况下增大此电压。因此在设计驱动电压形式时应尽可能减小tb(视电子器件所能达到的最短的关断时间来定),并选择较安全的高开启电压Uopen,然后根据式(13)确定ta。
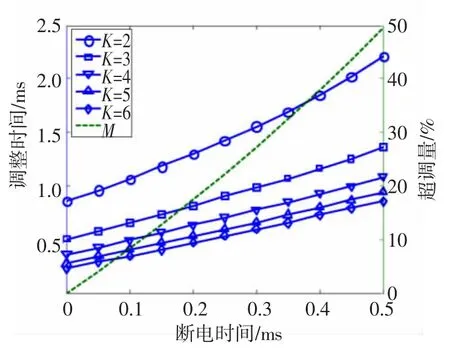
图11 ts和M随tb的变化曲线Fig.11 Curves of relationships between ts,M and tb
4.2驱动电压参数设计
下面分析断电时间与开启电压对致动器电流的影响。维持电压Uhold设定为24 V,开启电压Uopen为72 V(K=3),得到断电时间tb分别为0.5,0.25,0.1,0.05,0.01 ms时的电流仿真曲线如图12所示。由仿真结果可知,tb对超调量M和调节时间ts均有影响,且影响效果比较明显,当tb由0.5 ms减小至0.05 ms,系统超调量由50%减小至5%以下,调节时间也减小了至0.7 ms左右。但由于tb不影响电流的初始增长过程,由0.05 ms继续减小时,tb对ts影响不大。
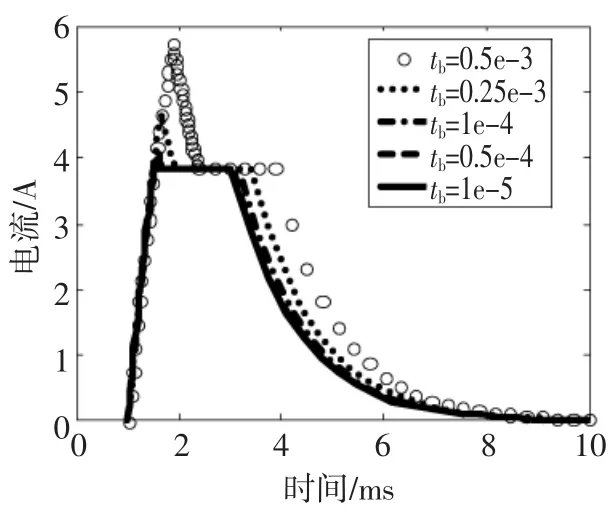
图12 不同断电时间对电流的影响Fig.12 Effect of tbon the energized current
令断电时间tb=0.1 ms,电压比K分别设定为2,3,4,5,6,得到不同开启电压时致动器电流仿真曲线如图13所示。由仿真结果知,增大开启电压不影响电流超调量M,但能有效减小调整时间ts,K从2增大至5时(Uopen由48 V增大至120 V),ts由大于1 ms减小至0.4 ms左右。而且由于K对初始电流增长率有影响,继续增大开启电压值可进一步减小ts,但不应超过电子器件的耐压。
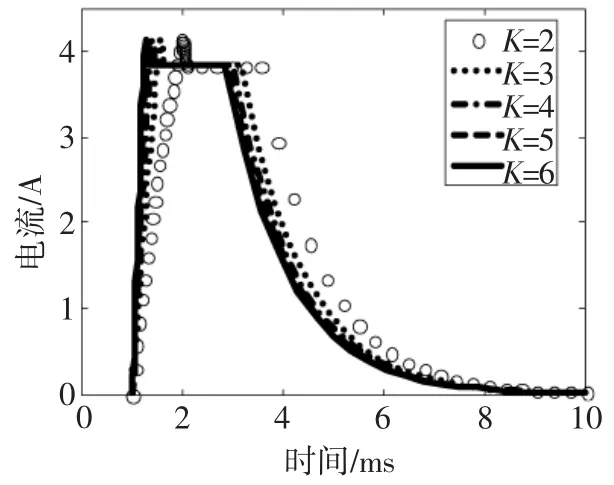
图13 不同开启电压对电流的影响Fig.13 Effect of Uopenon the energized current
综上所述,为使致动器线圈电流具有较低的电流调整时间及较小的超调量,断电时间tb应不高于0.05 ms(视电子元件开关能力,越低越好),开启电压Uopen应在保证器件长时间安全工作的前提下越大越好。
5 结论
1)以喷油器用超磁致伸缩致动器为例,对比了3种形式的致动器等效电路,以阻抗模和相角的相对误差最小为评判标准,确定了带并联电阻的等效形式最为有效,与实验结果的相对误差小于7%,说明了等效模型较为准确。
2)对带并联电阻的等效形式进行瞬态特性分析,通过对不同持续时间下初值的分别考虑,得到较准确的上升及下降电流表达式;借助实验系统测得电流瞬态值,实验结果与等效电路计算结果吻合,从而验证了等效模型在描述电流瞬态特性方面的准确性。
3)基于等效电路分析了适用于喷油器用超磁致伸缩致动器的驱动电压形式,并对其中的参数进行了优化设计,所设计的驱动波形能降低线圈电流的调整时间及超调量,取得了良好的效果。
[1]CLARK A E,LINDGREN E A.Development of Terfenol-D transducer material[J].Journal of Applied Physics,1998,83 (11):7282-7284.
[2]王博文,曹淑瑛,黄文美.磁致伸缩材料与器件[M].北京:冶金工业出版社,2008.
[3]卢全国,陈定方,魏国前,等.GMM的发展现状及其在精密致动器件中的应用[J].湖北工业大学学报,2006,21(3):92 -94. LU Quanguo,CHEN Dingfang,WEI Guoqian.Development of giant magnetostrictive materials and its application in the field of precision actuators[J].Journal of Hubei University of Technology,2006,21(3):92-94.
[4]李跃松,朱玉川,吴洪涛,等.射流伺服阀用超磁致伸缩执行器磁场建模与分析[J].兵工学报,2010,31(12):1587-1592. LI Yuesong,ZHU Yuchuan,WU Hongtao,et al.The magnetic field modelling and analysis of giant magnetostrictive actuator for jet servo valve[J].Journal of China Ordnance,2010,31(12):1587 -1592.
[5] BRAGHIN F,CINQUEMANI S,RESTA F.A low frequency magnetostrictive inertial actuator for vibration control[J].Sensors and actuators A:Physical,2012,180:67-74.
[6]TING Zhang,BIN Tang Yang,HONG Guang Li,et al.Dynamic modeling and adaptive vibration control study for giantmagnetostrictive actuators[J].Sensors and actuators A:Physical,2013,190:96-105.
[7]宣振兴,邬义杰,王慧忠,等.超磁致伸缩材料发展动态与工程应用研究现状[J].轻工机械,2011,29(1):116-119. XUAN Zhenxing,WU Yijie,WANG Huizhong,et al.Development and applications research on giant magnetostrictive materials [J].Light Industry Machinery,2011,29(1):116-119.
[8]杨兴,贾振元,武丹,等.基于功率MOSFET的超磁致伸缩执行器驱动源[J].压电与声光,2001,23(1):33-36. YANG Xing,JIA Zhenyua,WU Dan,et al.Study on driving power of giant magnetostrictive actuator based on power MOSFET[J]. Piezoelectrics&Acoustooptics,2001,23(1):33-36.
[9]葛荣杰,邬义杰,徐君,等.基于通用运放的GMA用大功率恒流驱动源设计[J].机床与液压,2008,36(2):5-7. GE Rongjie,WU Yijie,XU Jun,et al.Study on great power constant current power amplifier of GMA based on general operational amplifier[J].Machine Tool&Hydraulics,2008,36(2):5-7.
[10]Won-jong Kim,Ali Sadighi.A novel low-power linear magnetostrictive actuator with local three-phase excitation[J].IEEE Transactions On Magnetics,2010,15(2):299-307.
[11]王松,赵祥模,惠飞,等.基于DSP的超磁致伸缩换能器驱动电源设计[J].电子设计工程,2012,20(12):96-67,102. WANG Song,ZHAO Xiangmo,HUI Fei,et al.Design of rareearth magnetostrictive transducer based on DSP[J].Electronic Design Engineering,2012,20(12):96-98,102.
[12]李永,林明星,张承瑞,等.超磁致伸缩致动器功率驱动器设计[J].电机与控制学报,2013,17(7):22-26. LI Yong,LIN Mingxing,ZHANG Chengrui,et al.Power driver design of giant magnetostrictive actuator[J].Electric Machines and Control,2013,17(7):22-26.
[13]贾振元,郭东明.超磁致伸缩材料微位移执行器原理与应用[M].北京:科学出版社,2008.
[14]薛光明,何忠波,李冬伟,等.超磁致伸缩棒磁场强度建模及线圈优化分析[J].纳米技术与精密工程,2014,12(2):85 -90. XUE Guangming,HE Zhongbo,LI Dongwei,et al.Magnetic field intensity model for giant magnetostrictive rod and coil optimization analysis[J].Nanotechnology and Precision Engineering,2014,12(2):85-90.
[15]彭张.基于压电陶瓷的柴油机电控喷油器的研究[D].武汉理工大学,2010.
[16]袁文华,鄂加强,龚金科.柴油机高压共轨喷油系统设计优化及智能控制[M].北京:中国水利水电出版社,2014.
(编辑:刘琳琳)
Equivalent circuit and driving voltage suitable for giant magnetostrictive actuator in electric injector
XUE Guang-ming1, ZHANG Pei-lin1, HE Zhong-bo1, SUN Ye-zun2, LI Dong-wei1
(1.Vehicles and Electrical Engineering Department,Ordnance Engineering College,Shijiazhuang 050003,China;2.247 Military Representative Office,GAD Military representative Bureau,Taiyuan 030009,China)
Raising time of the current within the giant magnetostrictive actuator,with a winding inside,is always considerably long for the big inductance of the winding,and then the requirement of quick response could not be satisfied.To solve this problem,equivalent circuit for calculating precise current of the actuator was analyzed and suitable format of the driving voltage was designed.Three kinds of equivalent circuits were considered,and the equivalent form with a parallel-resistance inside was selected as the most effective one for its best description on the impedance of the actuator.The current equation of the best equivalent circuit,under square voltage input,was calculated and then the transient responses under different frequencies were achieved.Experimental impedance of the actuator and transient current within the winding was compared with the calculated results to validate the equivalent circuit.Based on the equivalent form with a parallel-resistance inside,efficient form of the driving voltage,with the high-switching-voltage technology employed,was designed and inside parameters were optimized.The calculated results show that the driving voltage designed reduces the modulating time of the current effectively with little overshoot.
giantmagnetostrictiveactuator;equivalentcircuit;impedance;transientresponse;driving voltage
10.15938/j.emc.2016.03.004
TM 131;TM 303
A
1007-449X(2016)03-0020-09
2015-04-16
国家自然科学基金(51275525)
薛光明(1990—),男,博士研究生,研究方向为超磁致伸缩材料的特性及应用、超磁致伸缩喷油器的优化设计及智能控制;
张培林(1955—),男,博士,教授,博士生导师,研究方向为车辆故障诊断及智能材料在车辆中的电子控制;
何忠波(1968—),男,博士,教授,博士生导师,研究方向为超磁致伸缩材料的应用和关重器材的保障;
孙也尊(1988—),男,硕士,助理工程师,研究方向为车辆底盘性能提升设计;
李冬伟(1979—),男,博士,讲师,研究方向为超磁致伸缩致动器的优化设计。
薛光明
