电网电压不对称跌落时DFIG的控制策略研究

朱晓荣，刘世鹏



电网电压不对称跌落时DFIG的控制策略研究

朱晓荣，刘世鹏

(新能源电力系统国家重点实验室(华北电力大学), 河北 保定 071003)

相比于对称故障，不对称故障时双馈风力发电机(Doubly Fed Induction Generators, DFIG)的电磁暂态过程更为复杂，对DFIG造成的危害也越大。从电网电压不对称跌落时DFIG的电磁暂态过程入手，分析了DFIG各电磁量产生二倍频波动和过电流的直接原因。在此基础上，提出了一种电网电压不对称跌落时转子侧变换器(Rotor Side Converter, RSC)的转子电压补偿控制策略，通过控制RSC交流侧的输出电压，对转子暂态电动势和负序电动势进行补偿。该控制策略可在电网轻度不对称故障时有效消除转子电流二倍频波动；在电网严重不对称故障时最大限度地减小转子电流冲击，增强DFIG的低电压穿越能力。此外，根据转子侧变换器的电压容量，对补偿控制策略的完全补偿范围进行了分析。仿真结果验证了所提出控制策略的有效性。

双馈风电机组；电网电压不对称跌落；低电压穿越；转子电压补偿；滑模控制

0 引言

电网电压不平衡时，双馈风力发电机(Doubly Fed Induction Generators, DFIG)会产生复杂的电磁暂态过程[1-4]。这会对DFIG的稳定运行造成十分不利的影响，比如，转子电流和定子电流的不平衡发热；输出有功功率和无功功率波动；电磁转矩振荡，造成机械系统的磨损、老化[1-3]。当电网发生严重不对称故障时，其造成的危害比对称故障更为严重[1]。此时转子中会产生很大的冲击电流，严重威胁转子侧变换器(Rotor Side Converter, RSC)的安全运行。

目前，不对称电网电压下DFIG的改进控制策略已经成为当前研究的热点问题。电网电压轻度不对称跌落下的主要控制目标是抑制DFIG各电磁量的二倍频波动。文献[4]提出了一种正负序、双轴电流控制方案，通过在正反转同步坐标系中分别控制转子电流正负序分量，实现不同的不平衡控制目标。该方法需要复杂的正负序分解，存在固有延时，影响了控制策略的动态响应性能，且正负序电流指令的计算较为复杂。文献[5]提出一种快速正负序分解方法，改善了系统的控制性能。文献[6]提出了一种在定子静止坐标系中的比例-谐振控制方案，该方案不需要对转子电流进行正负序分解，但为获得转子电流指令，其他分量如定子电压，定子电流依然需要正负序分解。

电网电压严重跌落时的控制目标主要是抑制转子过电流，保证DFIG的不脱网运行。文献[7]在电网不对称故障时，向转子端注入与定子暂态磁链和负序磁链方向相反的暂态电流和负序电流，减小了转子电压冲击。由于需要注入转子暂态电流和负序电流，加重了故障过程中的转子冲击电流。文献[8]提出了一种暂态磁链跟踪控制方法，在电网故障时控制转子磁链与定子磁链相等，降低了转子电流冲击。该方法导致DFIG从电网吸收无功功率，不利于故障恢复。

本文首先详细分析了电网电压不对称跌落时DFIG的电磁暂态过程，指出DFIG各电磁量产生二倍频波动的直接原因。基于此，提出一种转子电压补偿控制策略，即通过控制RSC交流侧的输出电压，对转子暂态电动势和负序电动势进行补偿。该控制策略可在电网轻度故障时有效抑制转子电流一倍频波动和二倍频波动；在电网严重故障时可减小转子电流冲击，增强DFIG的低电压穿越能力。同时根据RSC的电压容量，对补偿控制策略的完全补偿范围进行了分析。最后，仿真结果验证了所提出控制策略的有效性。

1  电网故障时DFIG的电磁暂态过程

1.1 DFIG数学模型

定子侧和转子侧均采用电动机惯例，在两相静止坐标系下，DFIG的数学模型为[9]

式中：s,r分别为定、转子电压矢量；s，r分别为定、转子电流矢量；s，r分别为定、转子磁链；s，r分别为定、转子电阻；s，r分别为定、转子自感；m为定转子互感；r为转子电角速度。

由式(1)~式(4)可得转子电压方程，并转化到转子坐标系中为

图1转子侧等效电路

Fig. 1 Equivalent circuit of the rotor side

1.2 电网不对称故障时DFIG的瞬态响应

电网电压不对称故障时，定子磁链将感应出正序分量sf1、负序分量sf2和暂态直流分量sn，其表达式如式(6)所示[1]。

式中：s1和s2分别为定子电压正、负序分量；s为同步角频率；s为定子磁链总量，由式(3)获得。

定子磁链各分量在转子绕组中产生的反电动势如式(7)~式(9)所示[7]。

式中：rf1、rf2和rn分别为转子反电动势正序分量、负序分量和暂态直流分量；为转差率。

将式(5)写成频域的形式[7,10]，可得：

式中，r=rr。

根据式(10)的矢量关系，并结合式(7)~式(9)，可得电网不对称故障时在定子静止坐标系中的转子侧矢量图如图2所示。从图中可以看出，rf2的转速为-s，rn为直流量。若RSC不能提供与rf2和rn频率、幅值、相位均相同的输出电压rf2和rn，则转子电流中也将感应负序分量rf2和直流分量rn。rf2和rn在同步旋转坐标系中的频率分别为2s和s，分别表现为二倍频波动和一倍频波动。由于转子电流、定子电流、定子有功功率和无功功率、电磁转矩之间的耦合效应，这些电磁量中也将出现在相应的一倍频波动和二倍频波动，对DFIG的稳定运行造成十分不利的影响。

当电网发生严重不对称故障时，rf2和rn的幅值很高，可能远远超出RSC所能提供的最大输出电压。此时，转子绕组中将产生幅值很高的负序电流和暂态电流，严重威胁DFIG和RSC的安全运行。

图2电网电压不对称时转子侧矢量图

2  DFIG二阶滑模控制

DFIG转子侧通常采用矢量控制方法，通过双闭环PI控制实现定子输出有功功率和无功功率的解耦控制。这种控制方法具有参数整定困难，鲁棒性差等缺点。滑模控制是一种鲁棒控制，不仅能有效抑制系统内部参数摄动和外部扰动，而且具有良好的动态响应性能[11]。传统的滑模控制存在抖振现象，阻碍了其在实际中的应用。抑制抖振的一种有效的方法是采用二阶滑模控制，二阶滑模控制将不连续的控制作用在滑模量的高阶微分上，从而保证滑模量的一阶导数是连续的，理论上可以完全消除抖振[12]。因此，本文采用二阶滑模控制设计转子侧控制器。

将式(1)~式(4)转换到同步旋转坐标系，并采用定子电压定向，得到转子侧数学模型为

式中：rd，rq为转子电压轴分量；rd，rq为转子电流轴分量；s1=s-r为转差角速度。

定义功率流出为正，则DFIG定子输出有功功率和无功功率分别为

式中：sd，sq分别为定子电压轴和轴分量；sd，sq为分别为定子电流轴和轴分量。

转子侧变换器的控制目标是实现DFIG输出有功功率和无功功率的精确调节，因此本文采用如式(13)的切换函数。

式中：积分项是为了消除系统的静态误差；P和Q为正常数；s*，s*为有功功率和无功功率参考值。

根据滑模控制的设计方法，滑模控制的控制输入由开关控制和等效控制两个部分组成[13]。本文采用二阶滑模控制中的超螺旋算法设计系统的开关控制[12-13]。结合式(13)，得到开关控制为

式中，p1，p2，q1，q2为正常数。

最终，得到系统总的控制输入为：

3  转子电压补偿控制策略

3.1 控制策略的理论分析

由第1节的分析可知，不对称电网电压下，RSC必须准确提供与转子反电动势负序分量和自由分量幅值、相位、频率相同的输出电压，才能完全抑制转子电流一倍频波动和二倍频波动。

转子电流负序分量和自由分量在坐标系中表现为交流量。当转子侧控制器采用典型的PI控制时，其对交流量的调节能力有限，因此RSC不能准确提供相应的励磁电压以抑制转子电流波动。

当采用滑模控制时，转子侧滑模控制器通过有功功率和无功功率参考值直接获得RSC的调制电压。当电网不对称故障时，转子电流感应出负序分量和自由分量，造成有功功率和无功功率的一倍频和二倍频波动。此时，转子侧滑模控制器的功率参考值仍按稳态情况给定，因此对这部分转子电流波动成分的调节能力也是有限的。此时RSC不能准确提供相应的励磁电压以抑制转子电流波动。

由式(10)可得转子电流负序分量为

同理可得转子电流自由分量的表达式为

假设RSC能够对转子反电动势负序分量和自由分量进行完全补偿，则此时的转子侧矢量图如图3所示。可以看出，加入补偿控制后，转子电流负序分量和自由分量得以完全消除。此时转子侧正序电压rf1即为滑模控制的输出电压。滑模控制器通过控制输出电压rf1调节转子电流正序分量rf1，进而实现DFIG有功功率和无功功率的解耦控制。

图3转子电压补偿控制下的转子侧矢量图

然而，RSC的电压输出能力有限。当电网发生严重不对称故障时，转子绕组反电动势将大于RSC所能提供的最大输出电压，RSC无法对其进行完全补偿。仅考虑负序分量，此时的转子侧矢量图如图4所示。图中，r_max为RSC能够提供的最大输出电压。可以看出，当采用转子电压补偿控制时，RSC能够输出与转子反电动势负序分量相位相同的补偿电压，且幅值达到r_max。未加补偿时，RSC的输出电压由滑模控制器获得，由于其对负序分量的调节能力有限，RSC的输出电压存在滞后，且幅值往往不能达到r_max。通过对比可以看出，两种控制策略下转子电流均出现负序分量，但采用补偿控制策略时，其幅值明显减小。因此，当电网发生严重不对称故障时，采用转子电压补偿控制策略能够有效抑制转子电流冲击，增强DFIG的LVTR能力。

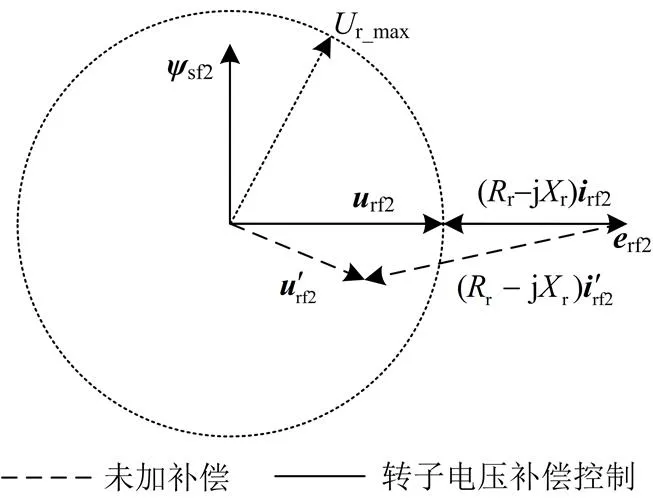
图4电网严重故障时转子侧矢量图

3.2 控制策略的实现

所提出的控制策略的控制框图如图5所示。该控制策略由RSC滑模控制器和转子电压补偿两部分组成。滑模控制对正序分量进行调节，实现DFIG输出功率的解耦控制。转子电压补偿控制在电网故障时抑制转子电流负序分量和暂态分量。图中，下标和分别代表两相静止坐标系和两相同步旋转坐标系。

图5转子电压补偿控制策略框图

由于该控制策略的控制目标是抑制转子电流负序分量和暂态分量，因此仅对rαβ2和rαβn进行补偿。得到补偿电压为

式中：rαβ2和rαβn由式(8)和式(9)获得；c1和c2分别为rαβn和rαβ2的补偿系数，其值在0~1之间。

最终，得到转子调制电压为

式中，rαβ_SMC为滑模控制的输出电压。经过SVPWM调制后，实现对DFIG的控制。

为补偿转子电动势负序分量，需要对定子电压进行正负序分解。本文采用文献[14]提出的快速正负序分解方法，其原理如图6所示，其中为系统角频率，为延迟角度。该方法仅仅需要简单的代数和延时运算，且最快可在一个采样周期内完成正负序分解。因此采用该方法可以实现对转子电动势快速精准的补偿，提高控制算法的动态响应性能和控制效果。

图6快速正负序分解

综上所述，所提出的转子电压补偿控制策略将补偿电压直接加在转子侧控制器的输出电压上，控制结构简单。快速正负序分解的引入提高了系统的动态响应性能。整个控制策略仅需要对定子电压进行正负序分解，简化了系统的设计。当电网故障时，该控制策略能快速响应转子侧电动势的变化，因而能够有效抑制转子电流波动。

3.3 转子电压完全补偿范围

RSC的补偿能力与其电压输出范围有关，当采用SVPWM调制算法时，RSC输出线电压的最大有效值为[15]

电网不对称故障时，转子绕组反电动势最大值为正序分量、负序分量和暂态分量的绝对值之和。由式(9)可知，暂态分量正比于定子暂态磁链，其幅值与故障类型和故障时刻有关[1]，本文仅考虑其幅值最大的情况：

由式(7)~式(9)可得转换到转子侧的转子绕组反电动势最大值为

式中：t为转子绕组与定子绕组的变比[15]；=|s2|/|s1|为不对称故障时的电网电压的不平衡度。

采用表1中所示的参数，根据式(21)和式(23)可得电网不对称故障时RSC的完全补偿范围如图7所示。图中实线为不同电网电压不平衡度下的转子绕组反电动势，虚线为RSC能够提供的最大输出电压。虚线以下的部分即为RSC的完全补偿范围，即采用转子电压补偿控制策略时，理论上可以完全消除转子电流的一倍频波动和二倍频波动。

可以看出，电网不对称故障时，RSC的完全补偿范围是有限的。提高直流侧电压可以拓宽RSC的完全补偿范围，提高DFIG的低电压穿越能力。

表1 仿真系统参数

图7不平衡电网电压下RSC的完全补偿范围

4  仿真研究

为验证本文所提出的控制策略，建立了风力发电系统仿真模型，系统的参数如表1所示。为了进行对比，设计了两种控制算法：算法(1)采用未加补偿的滑模控制，算法(2)采用转子电压补偿控制。

4.1 电网轻度故障

本文定义图7中虚线以下范围内的故障为轻度故障，即电网故障时的转子绕组反电动势小于RSC所能提供的最大励磁电压。

仿真开始时，DFIG以转速1.1 p.u.运行，定子输出有功功率为0.9 p.u.。=0.25 s时DFIG定子A相电压跌落至0.8 p.u.，造成7%的定子电压不平衡度。故障持续500 ms。补偿系数c1和c2取1。采用未加补偿的滑模控制策略和转子电压补偿控制策略的仿真结果分别如图8(a)和图8(b)所示。

图8电网轻度不对称故障时的仿真结果

由图7可知，电压跌落导致的转子反电动势在RSC的完全补偿范围之内。从图8(a)可以看出，未加补偿时，DFIG各电磁量均出现了一倍频波动和二倍频波动。加入补偿后，转子电流、定子电流、有功功率和无功功率的一倍频脉动和二倍频脉动基本得到消除，仅存在十分微小的波动。这是由于转子电压补偿指令需要经过RSC的调制才能作用到转子侧，这不可避免地会出现延时。电磁转矩的一倍频和二倍频波动依然存在，但与未加补偿相比，波动幅值明显减小。

由前面的分析可知，不加补偿时，转子侧控制器不能产生足够的励磁电压对转子电流自由分量和负序分量进行有效的抑制。从图8可以看出，未加补偿时的RSC调制电压(坐标系下，即rd和rq)较小。加入补偿电压以后，rd和rq幅值增大，但没有超过输出电压最大值，与理论分析的结果一致。

4.2 电网严重故障

电网故障前，DFIG以转速0.8 p.u.运行，定子输出有功功率为0.5 p.u.。=0.25时电网发生A相短路故障，导致DFIG定子A相电压跌落至0.2 p.u.，故障持续625 ms。为便于比较，在仿真过程中保护装置始终不动作。采用未加补偿的滑模控制策略和转子电压补偿控制策略的仿真结果分别如图9(a)和图9(b)所示。

电网严重故障时，转子侧控制器的控制目标是减小转子电流冲击，保证DFIG的不脱网运行。从图9可以看出，加入补偿后，转子电流幅值被限制在2 p.u.以内。定子电流、定子有功功率和无功功率、电磁转矩的振荡幅值也得到了明显的抑制。进入稳态后，由负序分量引起的转子电流、定子电流、有功功率和无功功率、电磁转矩的二倍频波动也得到了明显的减小。由于加入了补偿电压，转子输出电压明显增大，达到饱和，与理论分析的结果一致。

4.3 DFIG故障穿越范围

当采用转子电压补偿控制策略时，本文以转子电流不超过2 pu为限，测试了DFIG在不同输出有功功率和无功功率时的故障穿越范围，如图10所示。图中曲面以下部分为DFIG的安全运行区域，曲面以上部分为非安全运行区域，此时必须采取其他措施才能保证DFIG的不脱网运行。随着DFIG输出有功功率和无功功率的增加，DFIG的安全运行范围减小，这是由于随着DFIG输出有功功率的增大，转子转速升高，故障时产生的转子绕组反电动势就越大。此外，故障时DFIG输出的有功功率和无功功率越大，转子电流稳态幅值就越大，转子稳态电流与暂态电流叠加，更容易引起过流。

图10 电网不对称故障下DFIG的穿越范围

5  结论

本文在分析了电网不对称故障时DFIG的电磁暂态过程的基础上，提出一种电网电压不对称跌落时的转子电压补偿控制策略。可以得出以下结论：

(1) 电网轻度故障时，该控制策略可有效抑制转子电流的一倍频波动和二倍频波动；

(2) 电网严重故障时，该控制策略可最大限度地减小转子电流冲击，增强DFIG的低电压穿越能力；

(3) 所提出的控制策略对定子电流、定子有功功率和无功功率、电磁转矩的一倍频波动和二倍频波动也能起到很好的控制效果；

(4) 根据RSC的输出电压容量，对补偿控制策略的完全补偿范围进行了分析。指出了提高直流侧电压有利于提高DFIG的低电压穿越能力。

[1] LOPEZ J, GUBIA E, SANCHIS P, et al. Wind turbines based on doubly fed induction generator under asymmetrical voltage dips[J]. IEEE Transactions on Energy Conversion, 2008, 23(1): 321-330.

[2] 郑涛, 魏占朋, 李娟, 等. 计及撬棒保护的双馈风电机组不对称短路电流特性分析[J]. 电力系统保护与控制, 2014, 42(2): 7-12.

ZHENG Tao, WEI Zhanpeng, LI Juan, et al. Unsymmetrical short circuit current analysis of doubly fed induction generators with crowbar protection[J]. Power System Protection and Control, 2014, 42(2): 7-12.

[3] 何山, 王维庆, 张新燕, 等. 双馈风力发电机多种短路故障电磁场仿真研究[J]. 电力系统保护与控制, 2013, 41(12): 41-46.

HE Shan, WANG Weiqing, ZHANG Xinyan, et al. Simulation study of multiple short-circuit fault electromagnetic field about DFIG in wind power[J]. Power System Protection and Control, 2013, 41(12): 41-46.

[4] XU L, WANG Y. Dynamic modeling and control of DFIG-based wind turbines under unbalanced network conditions[J]. IEEE Transactions on Power Systems, 2007, 22(1): 314-323.

[5] 胡胜, 林新春, 康勇, 等. 一种双馈风力发电机在电网电压不平衡条件下的改进控制策略[J]. 电工技术学报, 2011, 26(7): 21-29.

HU Sheng, LIN Xinchun, KANG Yong, et al. An improved control strategy of doubly-fed induction generator under grid voltage unbalance[J]. Transactions of China Electrotechnical Society, 2011, 26(7): 21-29.

[6] 胡家兵, 贺益康, 王宏胜. 不平衡电网电压下双馈感应发电机转子侧变换器的比例–谐振电流控制策略[J]. 中国电机工程学报, 2010, 30(6): 48-56.

HU Jiabing, HE Yikang, WANG Hongsheng.Proportional- resonant current control scheme for rotor-side converter of doubly-fed induction generators under unbalanced network voltage conditions[J]. Proceedings of the CSEE, 2010, 30(6): 48-56.

[7] 杨淑英, 陈刘伟, 孙灯悦, 等. 非对称电网故障下的双馈风电机组低电压穿越暂态控制策略[J]. 电力系统自动化, 2014, 38(18): 13-19.

YANG Shuying, CHEN Liuwei, SUN Dengyue, et al. LVRT transient compensation strategy for doubly fed wind turbines under asymmetrical grid faults[J]. Automation of Electric Power Systems, 2014, 38(18): 13-19.

[8] XIAO S, YANG G, ZHOU H, et al. An LVRT control strategy based on flux linkage tracking for DFIG-based WECS[J]. IEEE Transactions on Industrial Electronics, 2013, 60(7): 2820-2832.

[9] HAO Zhenghang, YAO Zhiqing, LI Shaohua, et al. The contribution of double-fed wind farms to transient voltage and damping of power grids[J].Tehnicki Vjesnik, 2015, 22(1): 43-49.

[10] LOPEZ J, SANCHIS P, GUBIA E, et al. Control of doubly fed induction generator under symmetrical voltage dips[C] // IEEE International Symposium on Industrial Electronics, IEEE, 2008: 2456-2462.

[11] 朱鑫, 刘俊勇, 刘洋, 等. 基于滑模变结构的含不平衡负荷微电网控制策略研究[J]. 电力系统保护与控制, 2015, 41(6): 25-32.

ZHU Xin, LIU Junyong, LIU Yang, et al.Study of micro- grid control strategy contained unbalanced load based on sliding-mode variable structure[J]. Power System Protection and Control, 2015, 41(6): 25-32.

[12] 孙宜标, 杨雪, 夏加宽. 采用鲁棒微分器的永磁直线同步电机二阶滑模控制[J]. 中国电机工程学报, 2007, 27(33): 6-10.

SUN Yibiao, YANG Xue, XIA Jiakuan. Second order sliding mode control for PMLSM using robust differentiator[J]. Proceedings of the CSEE, 2007, 27(33): 6-10.

[13] ZHU Xiaorong, LIU Shipeng, WANG Yi. Second-order sliding-mode control of DFIG-based wind turbines[C] // IET Renewable Power Generation Conference, IET, 2014: 1-6.

[14] LIANG Y. A new time domain positive and negative sequence component decomposition algorithm[C] // IEEE Power Engineering Society General Meeting, IEEE, 2003: 1638-1643.

[15] HU J, HE Y. DFIG wind generation systems operating with limited converter rating considered under unbalanced network conditions ——analysis and control design[J]. Renewable Energy, 2011, 36(2): 829-847.

(编辑 周金梅)

A control strategy of DFIG under unbalanced voltage dips

ZHU Xiaorong, LIU Shipeng

(State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources (North China Electric Power University), Baoding 071003, China)

Compared with symmetrical voltage fault, the electromagnetic transient process of the doubly fed wind generator (DFIG) under asymmetrical fault is more complex, which causes much harm to the DFIG. The immediate cause of the appearance of pulsation second order component in the rotor current and other variables of the DFIG is analyzed by analyzing the electromagnetic transient process in DFIG during unbalanced grid dips. According to this analysis, a rotor voltage compensation control strategy is proposed to eliminate the rotor current pulsation under slight voltage dip and to reduce the over-current in the rotor circuit under serious voltage dips. Under the proposed control strategy, the AC terminal voltage of the rotor side converter (RSC) is controlled to compensate the DC and negative sequence components of the electromotive force. The complete compensation range is analyzed according to the limited AC terminal voltage of the RSC. Simulation results validate the proposed control strategy.

doubly fed induction generators; unbalanced voltage dips; low voltage ride through; rotor voltage compensation; sliding mode control

10.7667/PSPC151020

2015-06-18；

2015-07-20

朱晓荣(1972-)，女，博士，副教授，研究方向为新能源发电及并网技术、电力系统分析等；E-mail: xiaorongzhu@ ncepu.edu.cn

刘世鹏(1990-)，男，通信作者，硕士研究生，研究方向为新能源发电及并网技术。E-mail: liushipeng90@foxmail.com