多尺度微分模式相似性角点检测算法

王富平，水鹏朗



多尺度微分模式相似性角点检测算法

王富平，水鹏朗

( 西安电子科技大学雷达信号处理国家重点实验室，西安710071 )

为了避免图像的边缘毛刺及对比度差异对角点检测产生的不利影响，提出了一种多尺度局部微分模式相似性的角点检测算法。算法在边缘轮廓提取的基础上，利用各向异性高斯方向导数(ANDD)滤波器提取每一个边缘像素的局部微分模式。考虑到单个像素的微分模式容易受边缘毛刺的影响，因此利用像素及其支撑区域的微分模式之间的相似性构建角点测度。最后将3个尺度下的测度融合为新的角点测度，实验结果显示，与已有的3种算法相比，提出的算法在检测准确率、错检率、定位精度以及重复率上均具有更好的性能。

边缘检测；多尺度；微分模式；角点检测

0 引 言

角点是图像中稳定的局部特征之一，在计算机视觉、机器学习中应用广泛，比如图像配准、目标识别和图像检索[1]。已有的角点检测算法大致上分为三类：基于模板，基于强度和基于轮廓的角点检测算法。

基于模板的检测算法根据预定义的角点模板与局部图像的相似性进行角点检测。SUSAN[2]根据圆形模板中心像素与其他像素之间的加权相似度构建角点测度。文献[3]则利用双圆环代替圆形模板，提高了算法的检测精度。基于强度的检测算法直接利用图像强度变化进行角点检测。Harris[4]和多尺度Harris[5]利用图像一阶微分自相关矩阵的主曲率来检测角点。这两类算法充分利用了角点处的局部强度变化特性，能准确地识别真实角点，但是受噪声的影响，算法容易在同质区域产生伪角点。

基于轮廓的角点检测算法则是在边缘轮廓提取的基础上，根据轮廓的几何特性进行角点检测。He[6]在曲率尺度空间(Curvature Scale Space, CSS)算法的基础上，利用局部支撑区域自适应地确定判决阈值，从而克服了CSS算法中阈值难以确定的问题。Awrangjebp[7]利用3个尺度下的点到弦距离累积(Chord to Point Distance Accumulation，CPDA)曲率积检测角点，该算法对噪声比较鲁棒，但相邻角点距离很近时，容易丢失角点。为此，Teng[8]根据轮廓像素之间位置的三角函数特性提出了两种改进的角点检测算法，有效地提高了角点分辨力。Shui[9]在轮廓检测的基础上，利用噪声鲁棒的各向异性高斯方向导数(Anisotropic Gaussian Directional Derivative，ANDD)滤波器来提取轮廓像素的方向微分，并提出了基于归一化残余面积(Residual Area，RA)的角点测度，该算法融合了基于轮廓和基于强度的算法优点。Zhang[10]则通过提取边缘上Gabor滤波器的归一化微分能量来检测候选角点。

以上算法中，基于轮廓上像素的微分信息的检测算法具有更高的检测准确率[9-10]。主要原因是算法通过轮廓提取避免了同质区的伪角点，同时利用方向微分滤波器能更精确地描述角点处的局部微分变化信息。但当图像中不同区域间对比度存在差异时，容易在一些非角点处产生强响应，导致伪角点。另外，此类算法只利用了每一个边缘像素本身的方向微分信息，构建的角点测度容易受边缘毛刺的影响。为此，本文利用边缘像素及其左右支撑区域的微分模式之间的相似性来构建角点测度，使得最终测度对图像对比度具有不变性。最后通过融合3个尺度下的角点测度，来增强噪声鲁棒性同时提高角点定位准确性。实验结果表明，本文算法在角点检测准确率、错检率、角点重复率上均优于对比算法。

1 各向异性高斯导数滤波器

通常使用的一阶高斯微分算子具有的各向同性尺度特性使得其在提取方向微分时容易产生模糊，为此，Shui引入了ANDD滤波器来精确提取方向微分信息[9]。ANDD滤波器可以表示为

其中：为尺度因子，为各向异性因子，=[n，n]。旋转式(1)就可以得到角度为的ANDD滤波器：

(2)

(3)

2 多尺度微分模式的角点检测

2.1 边缘检测和轮廓填充

算法首先检测并提取图像的二值边缘轮廓。但由于噪声的影响，提取的边缘图会出现细小的断裂，导致部分角点丢失。为此，首先以8邻域区域增长算法遍历二值边缘图，将边缘图中每一条连通的轮廓以单独的顺序链码的形式存储，即={1，2,¼,}。然后对于每一个轮廓的端点而言，如果以其为中心的5 pixels×5 pixels窗口内包含其它轮廓的端点，那么根据这两个端点的坐标，利用线性插值方式计算间隙中需要填充的像素位置，并将这些像素赋值为1以达到填充间隙的目的；如果窗口内包含其它轮廓上的非端点像素，就将此端点沿边缘的方向延伸到其它轮廓即可。对轮廓的填充有助于找回一些丢失角点和T型角点，同时提高了部分角点的定位精度。

2.2 基于微分模式相似性的角点测度

在基于微分滤波器的角点检测方法中，文献[9]和文献[10]只利用了像素本身的微分信息来检测角点，而文献[11]则只利用了像素的ANDD主方向来构建角点测度。图1(a)为16个方向的ANDD滤波器的空域示意图。事实上，边缘上的像素是否被判定为角点，和像素本身及周围像素都有密切关联。为此，本文借鉴文献[7]中的支撑区域的思想，引入了单边支撑区域的概念。对于轮廓上的像素而言，其左右两边个像素分别构成了的左支撑区域L()和右支撑区域R()，如图1(b)所示。那么轮廓像素的左右支撑区域及整个区域内的平均微分模式分别为

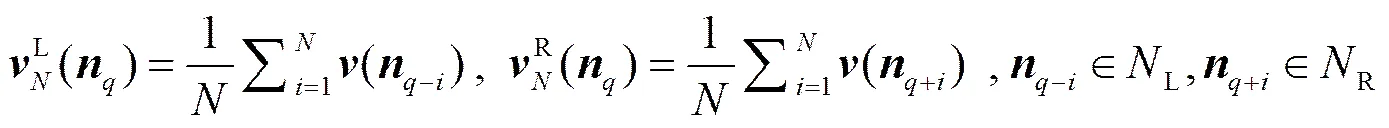
(5)

支撑区域内像素的ANDD微分模式有助于判定中心像素的类型。图1(c)是极坐标下显示的点及其L、R区域的ANDD微分模式。图1(d)~(f)分别是点处对应的微分模式。可以看出，简单边缘像素及其左右支撑区域的平均ANDD微分模式几乎一致，而由于多条不同方向边缘的影响，角点及其左右支撑区域的平均ANDD微分模式差异比较大。本文定义两个ANDD微分模式之间的相似度为

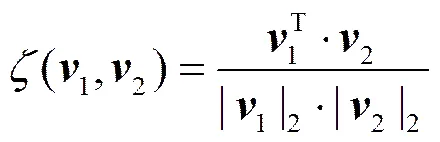
为了充分利用每一个轮廓像素本身及其支撑区域的微分模式，当支撑区域为时，提出的角点测度为

(7)

本文设定支撑区域的宽度为尺度参数，当比较小时，微分模式的角点定位性较好，但容易受边缘毛刺的影响产生伪角点。而当比较大时，区域内的均值平滑使得角点测度更加稳定，增强了噪声鲁棒性，但同时降低了部分角点的定位精度。为此，最终角点测度是3个尺度下的角点测度的几何平均：

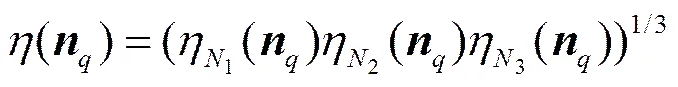
为了说明提出的测度有效性，分别利用CPDA[7]、RA[9]和本文算法计算图2(a)中的轮廓上每个像素的角点测度，该轮廓包含13个角点。图2(b)~(d)分别显示了3种算法的角点测度。图2(b)中CPDA角点测度曲线比较平滑，对边缘毛刺比较鲁棒，但其容易丢失强角点邻近的弱角点，如图中“○”所示。而图2(c)中基于RA的角点测度在角点处的响应十分明显，但由于受到图像对比度不均匀和边缘毛刺的影响，在非角点处容易产生大的响应，如图中“ÿ”所示。图2(d)中提出的角点测度继承了大尺度下测度的噪声鲁棒性，在非角点处响应值几乎为零，而且提出的角点测度充分利用了邻域像素和中心像素的微分模式之间的信息，构建的多尺度角点测度在角点与非角点处差异明显，设置简单的阈值就可以准确检测出真实角点。

图2 不同算法的角点测度比较

Fig.2 Comparison of corner measures of different algorithms

本文提出的基于多尺度微分模式相似性的角点检测算法的基本步骤如下：

步骤 1) 利用边缘检测算法提取图像中的边缘轮廓，并对轮廓上的间隙进行填充；

步骤 2) 利用式(2)构建个方向的ANDD滤波器，平滑轮廓并提取每一个像素处的ANDD微分模式；

步骤 3) 对于轮廓上的每一个像素，分别计算尺度1，2和3下其左支撑区域和右支撑区域的平均ANDD微分模式，进而得到单尺度下的角点测度1，2，3，然后带入到式(8)中，得最终融合角点测度;

步骤 4) 当角点测度大于设定的阈值时，就认定该像素是候选角点；

步骤 5) 对于每一个候选角点，如果其是5 pixel×5 pixel窗口内的最大值，就认定其为最终角点，否则将其剔除。

3 实验结果与分析

本文算法包括的可调节参数有：ANDD滤波器的尺度因子和各向异性因子，滤波器离散方向数，窗口尺度1，2和3以及最终判决阈值。其具体设置如下：对于算法中的ANDD滤波器而言，文献[11]指出，越小，ANDD滤波器受到周围结构影响的范围越小，其区分邻近角点的能力就越强，但要精确提取方向微分信息又要求滤波器具有强的各向异性，此时需满足>2。为了兼顾两者，本文采用文献[11]中的推荐参数2=2=6。滤波器离散方向数越大，ANDD滤波器的角度分辨率越高，提取的方向微分信息越丰富，同时对局部特征描述得越好，但算法计算量也会明显增加。为此，在滤波器具有不同的离散方向下，计算本文算法对于图3(a)中的9幅图像的平均角点配准率和错误检测率。图3(b)中显示，随着方向数的增大，角点检测准确率提高而错检率下降。当≥8时，检测准确率基本变化很小，但方向个数的增加导致滤波器的个数增加，使得提取ANDD微分模式的计算量明显增大，综合考虑算法计算量和检测准确率，本文选择=8。窗口尺度越小，越容易受噪声影响，使错检率上升，而过大又会过度平滑角点测度，使部分真实角点测度很小，导致正确检测率下降。为了选择合适的窗口尺度，令1在[1,6]上取值，2=21，3=31，从图3(c)中可以看出当尺度设置为1=3时，其平均配准率最高而错误检测率较小，因此本文中尺度参数为1=3，2=6，3=9。在角点检测中提高配准率和降低错检率是同等重要的，但从图3(d)中可以看出，随着角点判决阈值的增大，平均配准率和错检率都明显减小。通过计算配准率与错检率的差异，发现当0.08<<0.12时这种差异最大，所以，在实验中本文选择经验阈值=0.10。

图3 平均配准率和错检率随不同参数的变化

3.1 算法有效性实验

本实验包含36和249个参考角点的“Plane”和“Lab”图像[9-11],分别在无噪声和含噪声标准差为2=100两种情况下，利用CPDA[7]、RA[9]、Gabor[10]和本文算法检测图像角点，统计其配准角点、错误角点数目及定位误差。其它三种算法的程序和参数设置由原作者提供，本文算法的参数是：=8，2=2=6，1=3，2=6，3=9，=0.1。无噪声时的检测结果如图4所示，含噪声时的检测结果如图5所示。

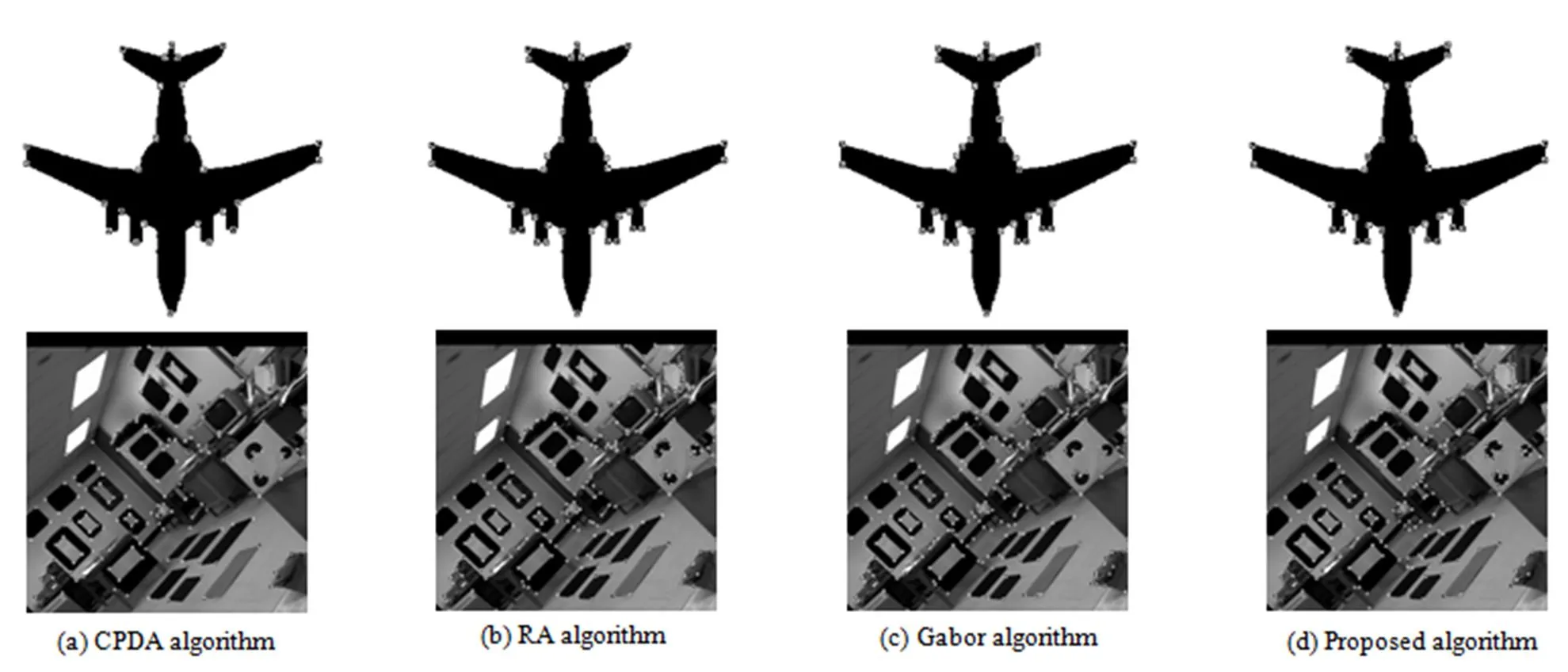
图4 无噪声下“Plane”和“Lab”图像检测结果

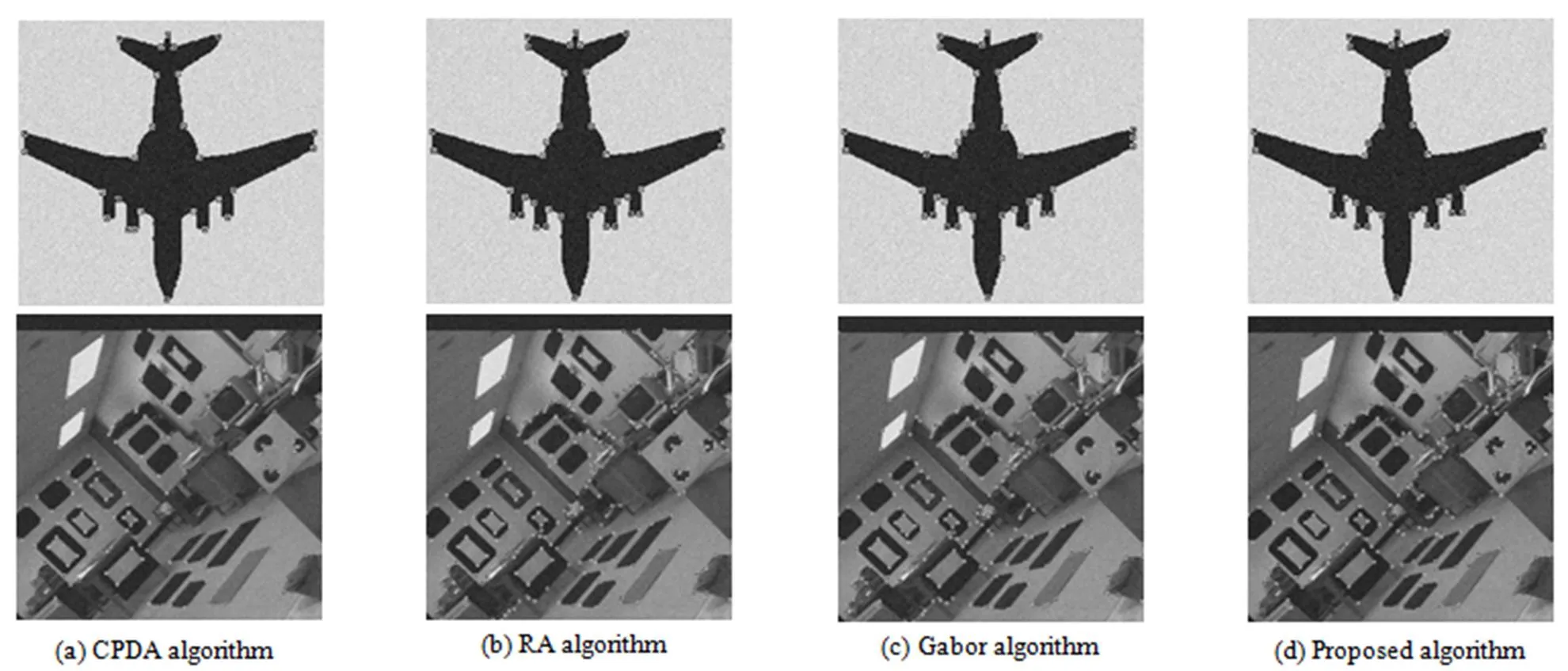
图5 含噪声ε2=100下“Plane”和“Lab”图像检测结果

从图4(a)可以看出，CPDA算法丢失了许多真实角点，这是因为CPDA使用了三个弦长(=10，20，30)对测度进行平滑，当相邻角点之间距离小于一定像素时，就无法区分开。而基于RA和基于Gabor的角点检测算法中使用的多方向局部微分信息相比曲率更能精确地描述角点处的特征，因此，图4(b)和图4(c)中两种算法的角点检测结果中的配准角点数目明显比CPDA多。但这两种算法中使用的方向导数滤波器又容易受到边缘毛刺的影响，会产生一些伪角点。图4(d)中可以准确地检测出真实角点，主要原因是局部支撑区将邻域的微分模式融入到最终角点测度中，使得算法具有很高的准确率。同时非角点支撑区域的微分模式相似性很强使得构建的角点测度几乎接近于零，降低了角点错检率，本文算法的错误角点的数目最少。

表1给出了无噪声和含噪声方差2=100时的四种算法的检测结果统计。为了公平比较，含噪声下的结果进行50次实验后的中值。无噪声情况下，CPDA算法检测到的配准角点数目和错误角点数目都最少，而其它三种算法的配准角点数目都明显比CPDA多。RA和Gabor算法受到边缘上对比度变化和边缘毛刺的影响，其错误角点数目也比较多。而本文算法在非角处微分模式的高度一致性使得最终角点测度很小，降低了角点错检率。CPDA和本文算法的检测结果变化不大，说明这两种算法的噪声鲁棒性很好。本文算法的测度对支撑区域的微分模式进行了平均处理，可以抑制边缘上的噪声和毛刺的影响，增强了算法的噪声鲁棒性。噪声导致边缘毛刺增多，而基于RA和基于Gabor的算法对于边缘毛刺相对比较敏感，导致错误角点数目明显增多。就噪声鲁棒性而言，CPDA算法最优，其次是本文算法，RA算法次之，Gabor算法最差。得益于小尺度下角点测度的定位准确性，本文算法的定位误差也相对比较小。在软件环境为Windows 7，Matlab 2010b，硬件环境是CPU 2.70 GHz，内存4 G的条件下计算四种算法的平均运行时间，如表1。Gabor、RA和本文算法都明显比CPDA算法的运行时间慢，这是由于这三种算法都用到了比较耗时的多方向微分滤波器，但这三种算法的检测结果明显优于CPDA。相比之下，本文算法和Gabor算法的运行时间比较接近，本文算法与RA算法都使用了ANDD滤波器来提取边缘上像素的微分信息，但本文算法对于两幅测试图像的运行时间分别是RA算法的33%(Plane图像)和25%(Lab图像)，运行时间明显比RA算法少。

表1 无噪声下和含噪声ε2=100时四种算法检测结果比较

3.2 重复率实验

角点重复率也是衡量角点检测算法性能的一个重要指标。假设原始图像和变换后图像中检测到的角点数目分别为0和T，其中重复角点为r个。那么，这组图像的角点重复率为a=(r/0+r/T)/2。对于文献[10]中的24幅测试图像(图6(a)显示了其中9幅图像)，分别计算四种算法在2种仿射变换和噪声干扰下的平均重复率。其中图像变换参数为：尺度变换中，坐标的尺度因子在[0.5，2]上采样；剪切变换('=+，'=)中剪切因子在[-1，1]上采样；高斯噪声干扰下的噪声标准差在[1，15]上采样。

四种算法的角点重复率如图6(b)~(d)，可以看出，尺度变换改变了图像大小，对边缘检测结果产生了影响，导致四种算法的平均重复率都下降。而本文算法融合了多尺度下的信息，具有一定的尺度鲁棒性，使得本文算法的重复率一直最高。剪切变换下，角点处的边缘轮廓的夹角发生了变化，使得四种算法的重复率都有所下降。而本文算法重复率最高，其原因是剪切变换虽然导致提取的ANDD微分发生了变化，但相邻像素的微分模式之间的相似性仍变化不大。而噪声干扰下，本文算法的重复率都最高。这是由于本文算法利用了支撑区间的多个像素的ANDD微分模式，相比CPDA、RA算法和Gabor算法，本文算法包含了更多的角点局部微分信息。因此，在角点重复率上，本文算法优于其它三种算法。

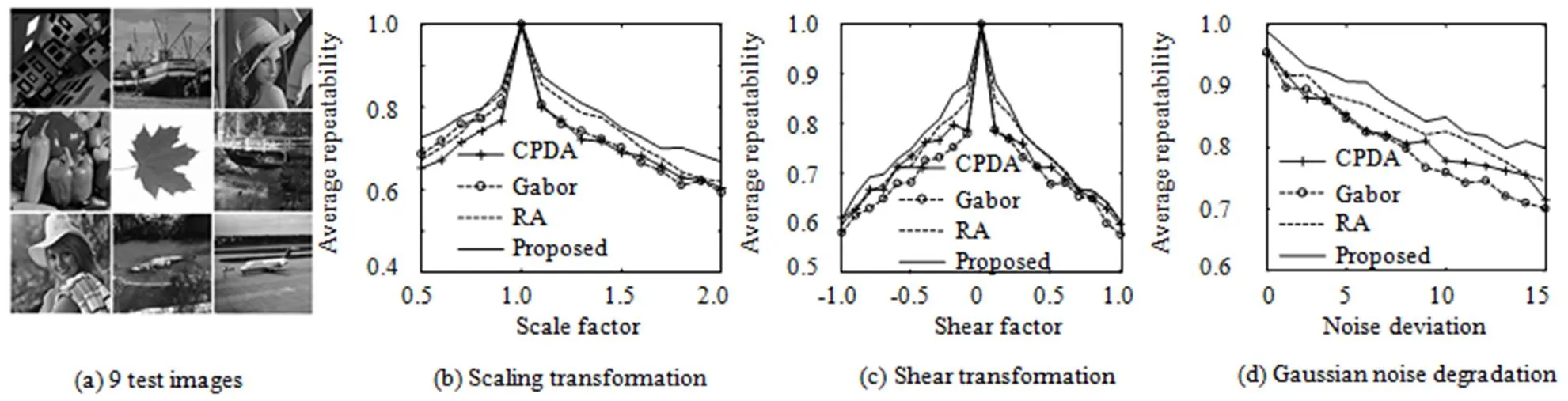
图6 不同图像变换下四种算法的重复率比较

4 结 论

本文提出了一种基于多尺度微分模式相似性的角点检测算法。不同于传统基于微分的方法中只利用像素本身的信息，本文算法将边缘像素支撑区域的微分信息融入到最终角点测度中，使得算法的检测性能更加稳定。同时，融合多尺度下的相似性角点测度既增强了算法噪声鲁棒性又提高了定位精度。实验结果显示，提出的算法在正确检测率、错检率和角点重复率上具有较好的性能。

参考文献：

[1] 毕国玲，赵建，续志军，等. 基于角点和局部特征描述子的快速匹配算法 [J]. 光电工程，2014，41(9)：63-68.

BI Guoling，ZHAO Jian，XU Zhijun，. A Fast Matching Algorithm Based on Corner and Local Feature Descriptor [J]. Opto-Electronic Engineering，2014，41(9)：63-68.

[2] Smith S M，Brady J M. SUSAN-a New Approach to Low Level Image Processing [J]. International Journal of Computer Vision(S0920-5691)，1997，23(1)：45-78.

[3] LAN Jinhui，ZHANG Meng. Fast and Robust Corner Detector Based on Double-circle Mask [J]. Optical Engineering(S0091-3286)，2010，49(12)：1-8.

[4] Harris C G，Stephens M J. A Combined Corner and Edge Detector [C]// Proceedings of the 4th Alvey Vision Conference，Manchester，England，August 31-September 2，1988：147-152.

[5] 王浩，周祚峰，曹剑中，等. 基于边缘轮廓上多尺度自相关矩阵的角点检测 [J]. 系统工程与电子技术，2014，36(6)：1220-1224.

WANG Hao，ZHOU Zuofeng，CAO Jianzhong，. Corner Detection via Multi-scale Autocorrelation Matrix on Edge Contours [J]. Journal of Systems Engineering and Electronics(S1004-4132)，2014，36(6)：1220-1224.

[6] HE Xiaochen，YUNG Nelson H C. Corner Detector Based on Global and Local Curvature Properties [J]. Optical Engineering(S0091-3286)，2008，47(5)：1-12.

[7] Awrangjeb M，LU Guojun. Robust Image Corner Detection Based on the Chord-to-Point Distance Accumulation Technique [J]. IEEE Transactions on Multimedia(S1520-9210)，2008，10(6)：1059-1072.

[8] TENG Shyhwei，Sadat R M，LU Guojun. Effective and Efficient Contour-based Corner Detectors [J]. Pattern Recognition(S0031-3203)，2015，48(7)：2185-2197.

[9] SHUI Penglang，ZHANG Weichuan. Corner Detection and Classification using Anisotropic Directional Derivative Representations [J]. IEEE Transactions on Image Processing(S1057-7149)，2013，22(8)：3204-3218.

[10] ZHANG Weichuan，WANG Fuping. Corner Detector using Gabor filters [J]. IET Image Processing(S1751-9659)，2014，8(11)：639-646.

[11] ZHANG Weichuan，SHUI Penglang. Contour-based Corner Detection via Angle Difference of Principal Directions of Anisotropic Gaussian Directional Derivatives [J]. Pattern Recognition(S0031-3203)，2015，48(9)：2785-2797.

Corner Detection Algorithm Using Multiscale Differential Mode Similarity

WANG Fuping，SHUI Penglang

( National Key Lab of Radar Signal Processing, Xidian University, Xi’an 710071, China )

To avoid theadverse effects of edge burrs and the difference of contrast ratio, a corner detection algorithm via multi-scale differential mode similarity is proposed. Based on the edge contour extraction, it extracts the local differential mode at each edge pixel by using the Anisotropic Gaussian Directional Derivative (ANDD) filters. Considering the fact that the differential mode at single pixel suffers from edge burrs, thus the similarity between the differential modes at a pixel and its support region is constructed as corner measure to enhance the stability of the corner measure. Finally, the measures at three scales are fused into a new corner measure to enhance the noise robustness and to improve the localization accuracy of corner measure. The experimental results show that the proposed algorithm behaves better performance in detection accuracy ratio, false detection ratio, localization and repeatability compared with three state-of-art algorithms.

edge detection; multi-scale; differential mode; corner detection

1003-501X(2016)10-0056-07

TP391.41

A

10.3969/j.issn.1003-501X.2016.10.010

2015-11-30；

2016-01-04

国家自然科学基金资助项目(61271295)

王富平(1987-)，男(汉族)，陕西兴平人。博士研究生，主要研究图像边缘、角点检测及其应用。E-mail: LD160811@163.com。