适于非线性机动目标跟踪的新IMM平滑算法
2016-10-13王美健吴小俊
王美健,吴小俊
适于非线性机动目标跟踪的新IMM平滑算法
王美健,吴小俊
( 江南大学物联网工程学院,江苏无锡 214122 )
针对非线性条件下机动目标跟踪问题,在此提出了一种增广交互式多模型容积卡尔曼滤波(AIMMCKF)算法。该算法将交互式多模型容积卡尔曼滤波(IMMCKF)应用到一个非线性状态增广系统,以得固定延迟平滑状态估计。同时,采用增广转换操作处理所用模型集中的不同模型可能属于不同状态空间的问题,保证算法能够正常进行。仿真结果表明,与传统非线性跟踪算法相比,所提算法在机动目标跟踪方面有更高的精度与更强的适应性。
机动目标跟踪;状态增广;容积卡尔曼滤波;非线性
0 引 言
近几十年来,在军事和民用方面目标跟踪技术均得到了广泛的关注,如何根据被跟踪目标的特点来建立相应的运动模型以及选择合适的滤波算法,是提高跟踪性能的关键。卡尔曼滤波[1](KF)是在线性最小均方根误差准则下进行目标状态估计的最优滤波算法,但是却不适合用于非线性情况。常用的非线性滤波算法有扩展卡尔曼滤波[2](EKF)、不敏卡尔曼滤波[2-3](UKF)、容积卡尔曼滤波[2,4-5](CKF)和粒子滤波[6-7](PF)等算法。
但以上这些算法均是基于单模型的滤波算法,能够对具有单一运动方式的目标有较好的跟踪性能。而实际的机动目标一般具有多种运动方式,以单一的运动模型来刻画其运动过程,往往和实际情况有较大的偏差,最终会因模型失配而导致跟踪误差增大甚至跟踪失败。因此,各种多模型估计得到了极大的研究关注,其中最具代表性的算法是交互式多模型(IMM)算法[8-9]。它集一阶广义伪贝叶斯[10](GPB1)计算上的优势及二阶广义伪贝叶斯[10](GPB2)良好的性能于一身,是一种较有效的混合估计算法。并且一系列改进的IMM算法也相继被提出,其中适合非线性情况下机动目标跟踪的有IMMUKF[11-12]、IMMEKF[13]及IMMCKF[14-15]等常用算法。
在文献[16]中提出的IMM固定时延平滑算法,是将IMM算法引入到状态增广系统内(故也可称AIMM算法),以此获得精度更好的固定时延平滑状态估计。而本文为改善非线性情况下机动目标跟踪的整体性能,提出一种AIMMCKF算法。该算法将IMMCKF算法应用到一个非线性状态增广系统中,同时针对算法所用的不同模型可能属于不同的状态空间,以相应的增广转换操作使各模型对应估计在交互混合与融合阶段处在相同空间。最后仿真结果表明,AIMMCKF算法能够在带来跟踪精度提高的同时,也较好地避免其他一些滤波器带来的缺陷,如当状态及协方差初始值误差较大时,EKF、UKF容易导致滤波器发散[17];并通过分析可知,在模型集的各模型属于不同空间的情况下,引入增广转换操作能保证算法的正常进行。
1 非线性状态增广系统描述
在此使用一种状态增广方式定义一个非线性状态增广系统。增广状态向量由状态向量增广所得:
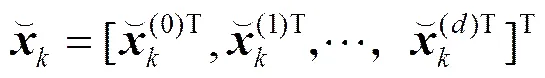
(2)
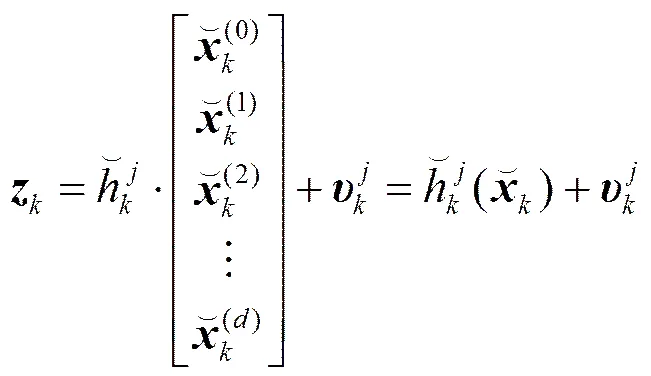
2 提出的算法
为得到非线性系统下的平滑状态估计,将IMMCKF算法引入到非线性状态增广系统内,并采用增广转换操作有效解决算法所用不同模型可能对应不同状态空间的问题。
2.1 增广转换操作
当多模型算法所用不同模型代表着不同状态空间时,为使算法中类似交互混合或结合的步骤能够正常进行,文献[18]采用了转换操作,使各模型对应估计在这些步骤能处在同一状态空间。在此主要简介常用的线性转换操作。假定有着不同状态空间的各模型状态与相同空间的状态,则:
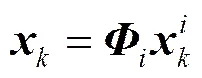
(5)
2.2 增广容积卡尔曼滤波算法
要处理增广形式的状态及其协方差,相应的滤波算法也应进行增广。在此将CKF[2,4-5]算法应用到第一节的非线性状态增广系统内形成增广容积卡尔曼滤波(ACKF)算法,其算法步骤:
1) 预测
2) 更新
预测测量容积点计算:

预测测量计算:
(7)
交叉协方差矩阵计算:
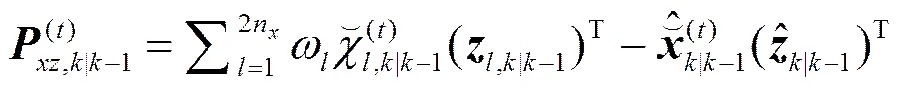
新息协方差矩阵计算:
(9)
其中R为时刻的测量噪声误差协方差矩阵。
卡尔曼增益计算:
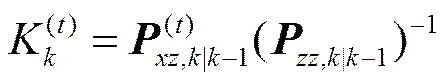
2.3 AIMMCKF算法
AIMMCKF算法是将IMMCKF算法引入到第一部分的非线性状态增广系统内,同时算法采用2.1部分的增广转换操作,使所用模型集中各模型对应的状态空间在交互混合与结合阶段相同,且保持其他阶段各模型处在原状态空间。算法的一个循环周期步骤如下(以下1)、5)与7)三个步骤的计算可参考文献[16]):
1) 混合权重计算。
2) 混合:
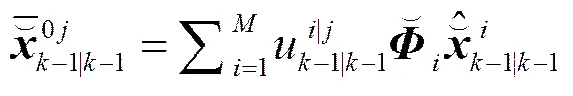
(12)
3) 滤波输入初始化:

(14)
4) 模型匹配滤波(ACKF滤波算法)。以上得到的增广混合状态及其协方差作为相对应的模型匹配滤波器的输入,再利用测量计算出、以及似然估计。
5) 滤波模型概率更新。
6) 状态估计和协方差综合:
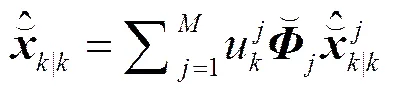
(16)
7) 平滑模型概率。
8) 固定延迟平滑状态及协方差输出:

(18)
3 仿真结果及分析
新算法的有效性阐明于两种仿真情况,仿真软件为MATLAB R2013a。传感器采样周期均为1 s,固定时延均取为3,蒙特卡洛运行次数均取为1 000。
情况1:目标的初始位置为(100 km,100 km),初始速度为(1 km/s,1 km/s),仿真时间为100 s,目标在21~40 s、61~80 s分别以角速度rad/srad/s进行匀角速度转弯运动,其他时间均进行匀速直线运动。仿真参数设置采用两个模型:模型1是过程噪声因子的匀速直线(CV)模型,且状态向量为;模型2是过程噪声因子、转率因子的未知转率的近协同转弯(NCT)模型,且状态向量为。显然,CV模型与NCT模型对应不同状态空间,为使各模型对应相同状态空间,设置转换矩阵如下:
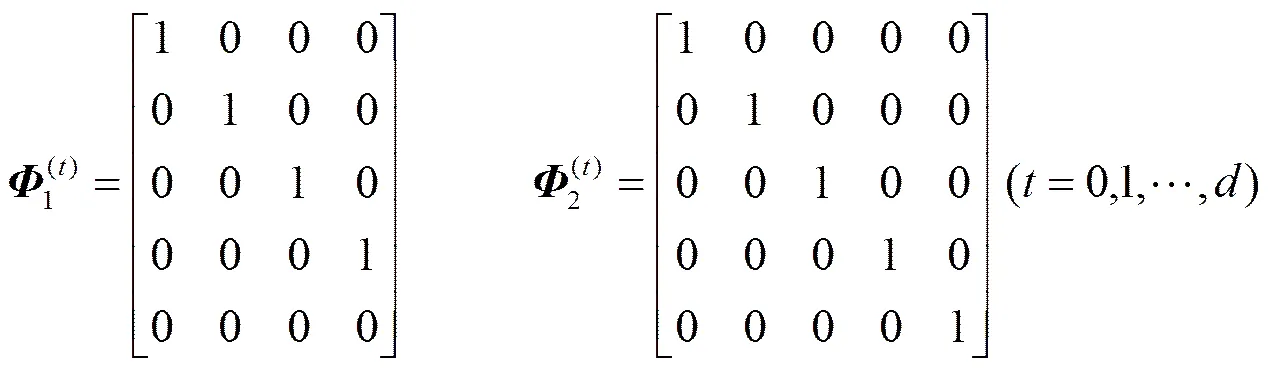
情况2:目标的初始位置在(4 700 m,1 200 m),初始速度为(-42 m/s,0 m/s),目标发生机动的时刻及加速度大小如表1所示。传感器的初始状态在(4 700 m,1 100 m),初始速度为(-10 m/s,-30 m/s),在1~45 s进行匀速直线运动,在46~52 s以加速度为(-5 m/s2,3 m/s2)的匀加速运动,最后48 s进行匀速直线运动。

CV模型、CA模型对应的状态转移矩阵以及NCT模型对应的非线性状态转移分别为
,,
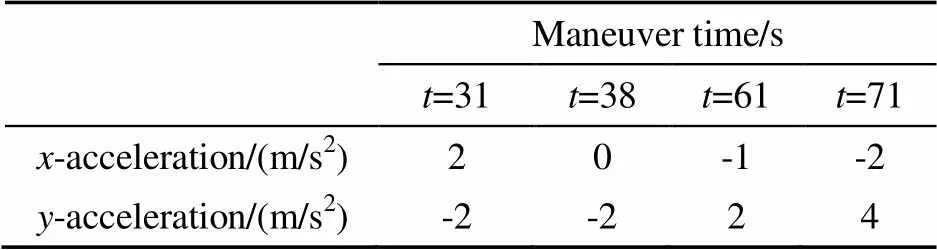
表1 目标机动情况表
情况1的仿真结果如图1到图5,情况2的仿真结果如图6到图10,其中图(a)表示各算法在状态初始值误差较小时所取得的仿真结果,图(b)为状态初始值误差较大时的仿真结果。由情况1的结果可得AIMMCKF算法的跟踪效果最好,在系统的非线性稍强情况下,机动目标的跟踪效果比AIMMEKF算法好很多;与IMMCKF比较可以看出,所得到的固定延迟平滑状态估计准确性较高于滤波状态估计。情况2属于稍弱的非线性系统下的机动目标跟踪。当状态初始值误差较小时,IMMCKF比IMMUKF算法的跟踪性能好些,且AIMMCKF与AIMMEKF算法的性能相近,比其余算法都好。当状态初始值较大时,AIMMEKF与IMMUKF算法容易出现发散,AIMMCKF与IMMCKF算法能较好解决这种情况。同样AIMMCKF相比于IMMCKF算法有显著性能优势。
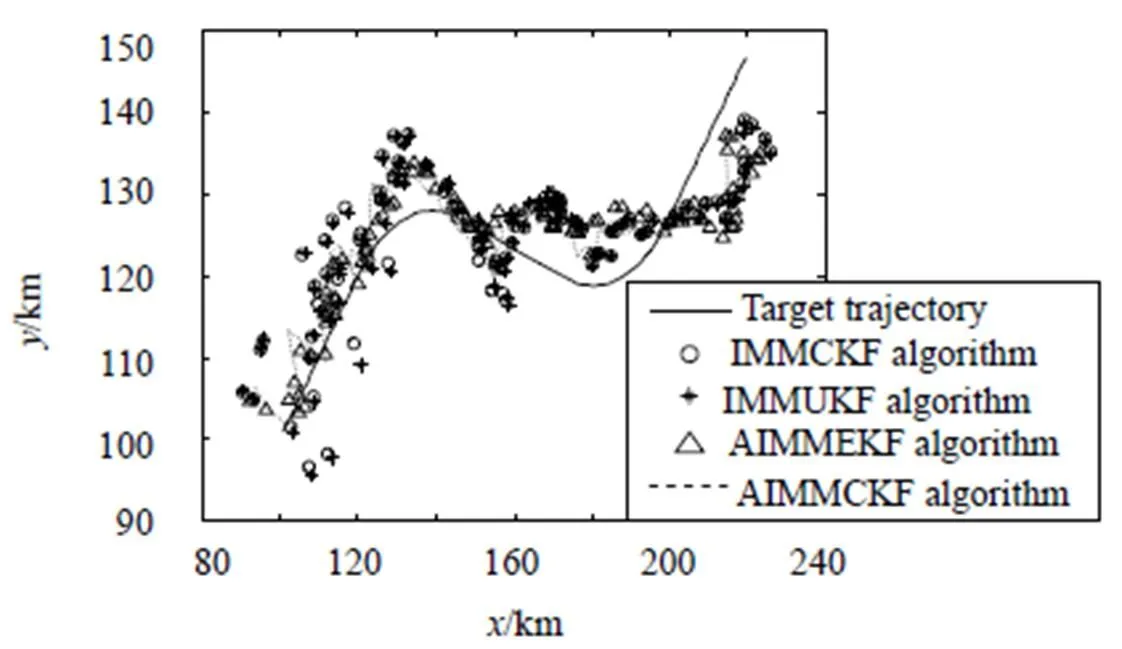
图1 目标位置的真实值与估计值

图2 x-位置均方根误差
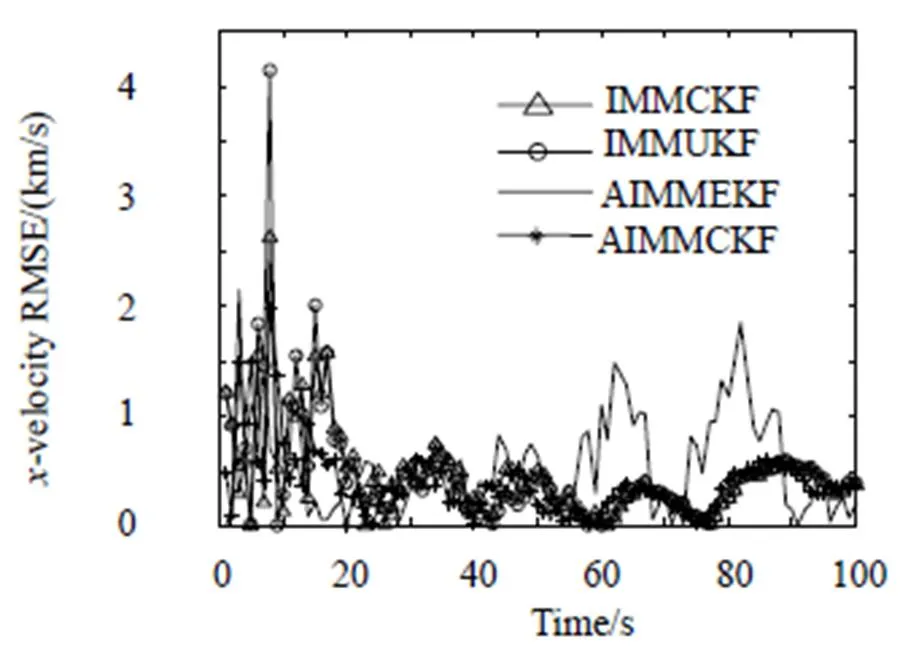
图3 x-速率均方根误差

图4 y-位置均方根误差

图5 y-速率均方根误差
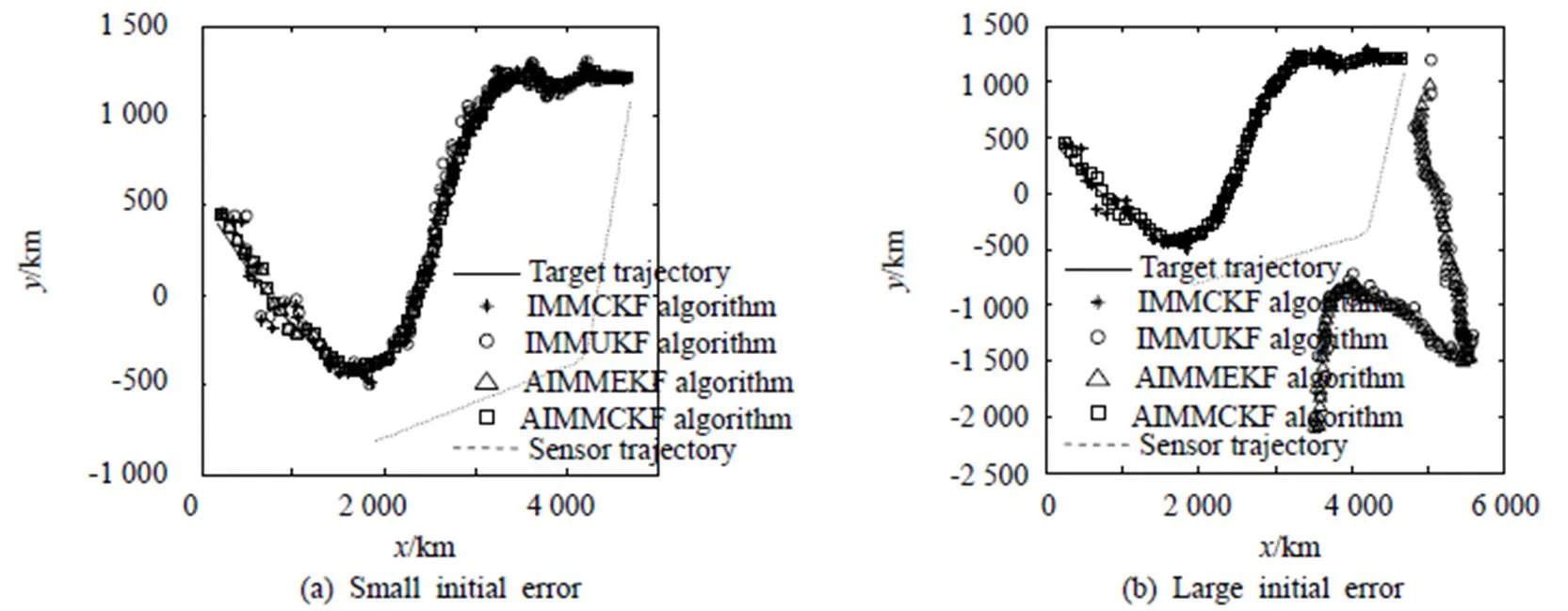
图6 目标位置的真实值与估计值

图7 x-位置均方根误差

图8 x-速率均方根误差

图9 y-位置均方根误差

图10 y-速率均方根误差
综合分析:在稍强非线性情况下,AIMMEKF算法因受滤波器EKF算法的影响,跟踪性能显著较差;在初始误差较大情况下,AIMMEKF与IMMUKF受滤波器影响容易出现发散;而AIMMCKF算法对机动目标跟踪有较好适应能力,不但能得到更优于滤波状态估计的固定延迟平滑状态估计,而且在状态初始误差较大时也容易出现滤波发散。对于仿真中不同模型对应不同状态空间,若采用低维添0使各模型处在相同状态空间的传统应对方式,传统IMMCKF与IMMUKF算法在运行过程中易出现异常,可能在低维添0方式不能保证如CKF、UKF等滤波算法中Cholesky分解的正常进行。尤其是不同模型对应状态空间存在很大差别时,其可行性可能更差。故本文将转换操作引入到传统IMMCKF、IMMUKF算法,而所提的增广算法也采用增广转换操作,以此较好地解决这方面问题。
4 结 论
本文提出的AIMMCKF算法,将IMMCKF算法应用到非线性状态增广系统中,得到性能更优的固定延迟平滑状态估计,同时也能避免其他一些传统算法由于滤波器带来的一些缺陷,如不太适应强非线性系统或初始误差较大容易导致跟踪性能较差,甚至出现发散。并且采取增广转换操作,解决算法中不同模型属于不同状态空间的问题,保证在跟踪过程中算法的正常进行。最后通过仿真结果证明了算法的有效性。需要指出,所提算法中的增广转换操作只列出常用的线性形式,若实际需要也可有效扩展到非线性形式。
参考文献:
[1] Haug A J. Bayesian Estimation and Tracking:A Practical Guide [M]. John Wiley & Sons,2012:70-74.
[2] DAI Hongde,DAI Shaowu,CONG Yuancai,. Performance Comparison of EKF/UKF/CKF for The Tracking of Ballistic Target [J]. Telkomnika(S2087-278X),2012,10(7):1537-1542.
[3] WU Yuanxin,HU Dewen,WU Meiping,. Unscented Kalman Filtering for Additive Noise Case:Augmented versus Nonaugmented [C]// American Control Conference,Portland,USA,June 8-10,2005:4051-4055.
[4] Ienkaran Arasaratnam,Simon Haykin. Cubature Kalman Filters [J]. IEEE Transactions on Automatic Control(S0018-1269),2009,54(6):1254-1269.
[5] Ienkaran Arasaratnam,Simon Haykin,Thomas R Hurd. Cubature Kalman Filtering for Continuous-Discrete Systems:Theory and Simulations [J]. IEEE Transactions on Signal Processing(S1053-587X),2010,58(10):4977-4993.
[6] Arulampalam M S,Maskell S,Gordon N,. A Tutorial on Particle Filters for Online Nonlinear/Non-gaussian Bayesian Tracking [J]. IEEE Transactions on Signal Processing(S1053-587X),2002,50(2):174-188.
[7] ZHAO Yunji,PEI Hailong. Object Tracking Based on Particle Filter with Discriminative Features [J]. Control Theory and Application(S2095-6983),2013,11(1):42-53.
[8] Henk A P Blom,Yaakov Bar-Shalom. The Interacting Multiple Model Algorithm for Systems with Markovian Switching Coefficients [J]. IEEE Transactions on Automatic Control(S0018-9286),1988,33(8):780-783.
[9] LI Xiaorong,Vesselin P Jilkov. Survey of Maneuvering Target Tracking [J]. IEEE Transactions on Aerospace and Electronic Systems(S0018-9251),2005,41(4):1255-1321.
[10] 夏佩伦. 目标跟踪与信息融合 [M]. 北京:国防工业出版社,2010:152.
XIA Peilun. Target Tracking and Information Fusion [M]. Beijing:National Defense Industry Press,2010:152.
[11] GONG Shuli,WU Honglan,TAO Cheng,. Tracking Maneuvering Target on Airport Surface Based on IMM-UKF Algorithm [C]// Optoelectronics and Image Processing,Haiko,China,November 11-12,2010,2:671-675.
[12] ZANG Rongchun,CUI Pingyuan,CUI Hutao,. Integrated Navigation Algorithm Based on IMM-UKF [J]. Kongzhi Lilun yu Yingyong/ Control Theory & Applications(S1000-8152),2007,24(4):634-638.
[13] Branko Ristic M,Sanjeev Arulampalam. Tracking a Maneuvering Target Using Angle-only Measurements:Algorithms and Performance [J]. Signal Processing(S0165-1684),2003,83(6):1223-1238.
[14] WAN Mingjie,LI Pengfei,LI Tao. Tracking Maneuvering Target with Angle-Only Measurements Using IMM Algorithm Based on CKF [C]// Communications and Mobile Computing,Shenzhen,China,April 12-14,2010,3:92-96.
[15] JIA Bin,Erik Blasch,Khanh D Pham. Space Object Tracking and Maneuver Detection via Interacting Multiple Model Cubature Kalman Filters [J]. IEEE Aerospace Conference(S1095-323X),Montana,USA,May 7-14,2015:1-8.
[16] CHEN Bing,Tugnait J K. Interacting Multiple Model Fixed-Lag Smoothing Algorithm for Markovian Switching Systems [J]. IEEE Transactions on Aerospace and Electronic Systems(S0018-9251),2000,36(1):243-250.
[17] YANG Wenbo,LI Shaoyuan,LI Ning. A Switch Model Information Fusion Filter Based on ISRUKF for Autonomous Navigation of Spacecraft [J]. Information Fusion(S1566-2535),2014,18:33-42.
[18] GAO Yongxin,LIU Yu,LI Xiaorong,. Multiple Model Estimation with Heterogeneous State Representation [C]// Conference on Information Fusion,Washington,DC,July 6-9,2015:1840-1847.
New IMM Smoothing Algorithm Suitable for Nonlinear Maneuvering Target Tracking
WANG Meijian,WU Xiaojun
( School of LoT Engineering, Jiangnan University, Wuxi214122, Jiangsu, China )
In order to solve tracking problem of maneuvering target in nonlinear background, an Augmented Interacting Multiple Model Cubature Kalman Filter (AIMMCKF) algorithm is put forward. To obtain the fixed-lag smoothing state estimation, IMMCKF approach is applied to a nonlinear state-augmented system in the proposed algorithm. At the same time, to tackle different models problem within being represented in different state spaces, corresponding augmented conversion operation can be used. The simulation results show that, the proposed algorithm achieves higher precision and stronger adaptability for maneuvering target tracking in comparison with traditional nonlinear tracking algorithms.
maneuvering targets tracking; state augmented; cubature Kalman filter; nonlinear
1003-501X(2016)10-0018-07
TP301.6
A
10.3969/j.issn.1003-501X.2016.10.004
2016-01-28;
2016-05-15
国家自然科学基金资助项目(61373055);江苏省研究生培养创新工程资助项目(KYLX_1123)
王美健(1989-),男(汉族),江西吉安人。硕士研究生,主要研究工作是信息融合与目标跟踪。E-mail: WMJian3617@126.com。
