基于巴特沃思滤波基准提取的专利技术研究

申丁

（福建省计量科学研究院，福建 福州　350100）

基于巴特沃思滤波基准提取的专利技术研究

申丁

（福建省计量科学研究院，福建 福州350100）

高斯滤波器因其构造、设计简单，且滤波特性具有零相移特性，目前已经是ISO 11562和ASME B46.1规定的基准提取方法，但由于其支撑域范围过大，一定程度影响到其在三维基准提取中效率［1］。为此，结合相关专利与文献，引入巴特沃思函数构建基于并行算法的高斯滤波算法，以提高其在实际工程应用中的效率。并将其运用到三维实例中，从中可以发现基于并行的算法所耗时间低于其他算法。

高斯滤波器；巴特沃思滤波器；并行算法

巴特沃思滤波器是利用巴特沃思函数所设计的高通、低通、带通和带阻滤波器的统称，广泛用于不同领域的研究和专利中。其最早由英国工程师Stephen Butterworth于上世纪三十年代提出。其主要特点在于通带内的频率响应曲线最平滑，但也存在截止频率处其过渡区间较长的不足。虽然学者也将其进行串行运算来逼近高斯滤波，最终也实现了较为快速基准提取［1-2］。通过实际应用发现，将其进行并行改进，算法的耗时将会进一步减少。由于基准提取中的高斯滤波器为典型的低通滤波器，因此也选取巴特沃思低频滤波器为研究对象。

其中，|H（jw）|为巴特沃思滤波器频域响应的幅值函数，w和wc分别为频率和截止频率，n为低通滤波器的阶次，为了简化，将其设置为1。巴特沃思滤波器在二维复坐标系上满足如下关系：

式（1-2）中的函数极点位于在实轴距离原点wc的位置，根据z变换和双线性变化可得巴特沃斯滤波的传递函数满足如下关系：

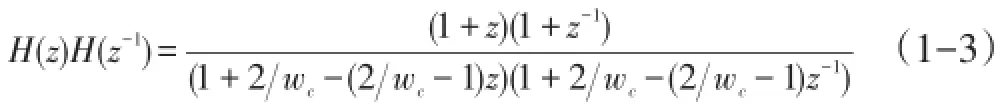
1　巴特沃思滤波拟合算法

实际滤波过程中，可以将一般的卷积运算化简为如下的差分形式［4］：

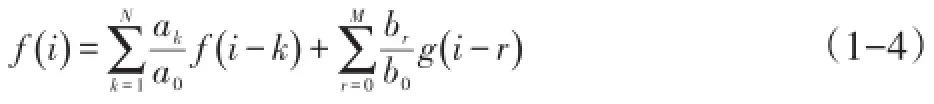
式中ak、br、M、N为滤波器常数，g（·）和f（··）分别为信号函数。公式（1-4）得出其滤波过程实际是对采样数据进行一系列的加法和乘法的运算。在计算机运算中，乘法计算的复杂程度明显会高于加法，因此通过减少算法中所含乘法的数量即可提高算法效率。普通高斯滤波器是典型的有限冲击响应滤波器（FIR），为了达到减少乘法的目的，可以通过使用无限冲击滤波（IIR）来拟合高斯滤波器，其主要推导过程如下：

高斯函数s（x）一般写成如下形式：

对其进行级数分解，形式如下：

当x 远小于1时，可以将上式等价于如下形式：

此时，高斯滤波器已转化为简单的无限冲击响应滤波器（IIR）。根据卷积定理，时域卷积的傅立叶变化等于频域的点积。而频域卷积的逆傅立叶变化等于时域的点积。这样对于高斯函数来说，无论是傅立叶变化还是逆傅立叶变化，其所得到的函数均为高斯函数，且自卷积和自乘积都是高斯函数。根据中心极限定理，得到更加逼近高斯滤波的方法，其推导过程如下：

对于点乘来说，高斯函数满足：

对于卷积来说，高斯函数同时满足：

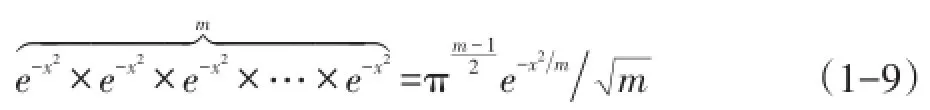
其中，×为卷积算子，m为运算次数。同时：

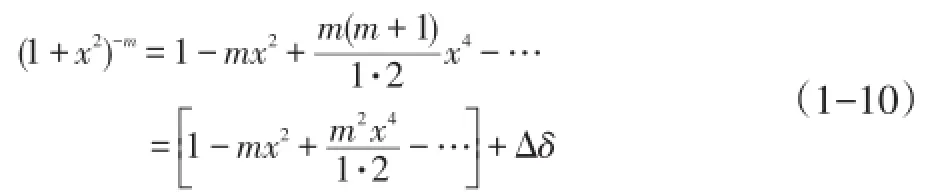
其中，Δδ为等式残差。根据等式（1-7）可以得到：

当x→0、m→∞，根据中心极限定理，Δδ→0，近似得到如下关系

对等式（1-5）进行傅立叶变换，得到高斯函数的频域响应函数。

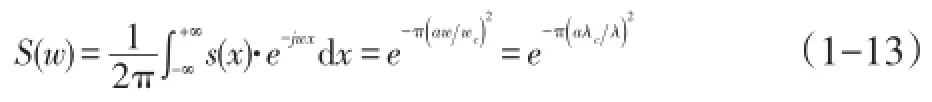
其中，λ为波长参数。因此，根据ISO11562定义高斯滤波器，其传输特性为：

从上述等式可以看出，高斯函数是一种典型的低通滤波器。为了使用无限冲击响应滤波器（IIR）来拟合高斯滤波器，通过使用等式（1-12）的1/（1+x2）来拟合等式（1-14），其定义如下函数：

按照ISO11562规定，当λ=λC时，滤波器的传输率为0.5（即Hβ（λCλ）=0.5），从而可以计算出不同级联阶次下β的取值，例如，当一级级联时，则β=1，（n=1）。

将此种并联拟合的思路引入巴特沃思滤波器（1-15）。可将级联滤波器传递函数如下表述：

式中n为其级联的阶次，a、b根据其截止波长λc、采样间隔Δx和n确定，对等式（1-16）进行并联改进，则A（z）的等式如下：

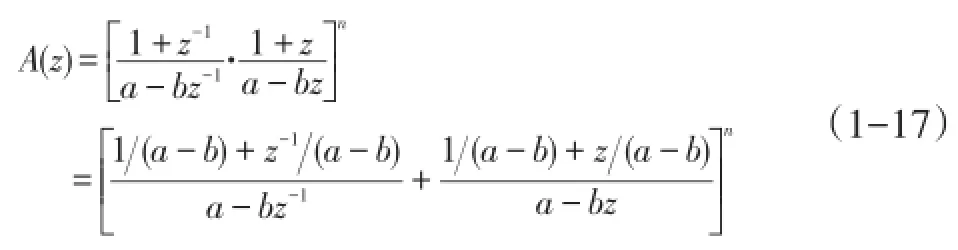
其中1/（a-b）=0.5。下面将列出并行运算的具体计算公式。

上式中，由于函数w1（k）、w2（k）可在计算机中同时计算且互不干扰，这种简单并行结构就大大减少了计算耗时，提高其在实际工程中的效率。

2　三维实例分析

用光学干涉仪对一实测研磨加工表面进行采集，如图2（a）所示。其中截止波长为 λc=50μm，取样间隔，Δx=1μm采样数据的大小为256×256。同样选择八阶级联滤波器逼近标准高斯滤波器，根据公式（1-15）可知，α= 5.7865、b=3.7865和1/（α-b）=0.5，最后用不同算法进行了表面粗糙度评定。

表1 计算耗时对比表（单位：s）

从表1可以看出，高斯滤波所耗时间是最长，基于串联拟合滤波所耗时间有所下降，但大于并联拟合滤波所耗时间，而并联形式耗时仅仅是0.0921s，说明改进的方法的高效性。

3　结语

通过提出基于并行巴特沃思滤波器快速拟合高斯滤波器的基准提取算法，大大提高了基准提取的效率。在三维实例中，改进算法所提取的三维表面基准，在保证粗糙度参数相差极小的基础下，耗时远远小于高斯滤波器和级联拟合滤波器，论证了并联方法的有效性，在相关基准提取专利和研究领域中具有很好的应用前景。

［1］王大伟，贾荣丛，王划一.基于Matlab的巴特沃斯滤波器设计［J］.现代电子技术，2012，35（21）：71-72.

［2］胡广书.数字信号处理：理论，算法与实现［M］.北京：清华大学出版社，2003.

The Technical Research of Reference Characterized Algorithm Based on Butterworth Filter

Shen Ding
（The Metrology Institute of Fujian Province，Fuzhou Fujian 350100）

Due to the convenience in design and zero phase- shift， the Gaussian Filter has been adopted in ISO 11562 and ASME B46.1 as a standard reference representation method. However， it always has bad performance and low efficiency in 3-D reference representation.Therefore，make use of the parallel Butterworth Filter to realized the traditional Gaussian Filter and increase its efficiency in reference representation based on related patents and theses.

gaussian filter；utterworth filter；parallel algorithm

TB921

A

1003-5168（2016）06-0074-02

2016-6-20

申丁（1988-），男，研究生，助理工程师，研究方向：振动和表面工程技术。