基于混合耦合与未知扰动的复杂网络同步研究

2016-10-13常安成纪晓燕田时宇

湖南科技学院学报 2016年5期

常安成　纪晓燕田时宇

常安成纪晓燕田时宇

（湖南信息学院，湖南长沙 410151）

文章主要讨论了一类带有外部扰动和混合时滞耦合的复杂网络模型，为了克服未知的外部对网络部分节点的扰动，并实现复杂网络的同步，通过设计一款自适应控制器，构造合适的Lyapunov函数，利用稳定性理论，对复杂网络的同步进行了严密的论证，证实了该理论成果的有效性。

复杂网络；自适应性；同步；鲁棒性

文章介绍了一类具备混合时滞和未知外部扰动的混合耦合复杂网络，通过设计一款简易的鲁棒自适应控制器来实现复杂网络的同步。网络被扰动是复杂的，我们考虑的是网络部分关键的节点被扰动，即使先前不知道被扰动的强度。必须强调的是，我们并没有假定耦合矩阵为对称矩阵或对角矩阵。但该控制器仍具有增强鲁棒性，降低复杂网络的脆弱性的特点，因此具备很强的现实意义。

1　预备知识与假设

一类由N个相同的节点同时具有混合时滞与外部扰动的混合耦合复杂网络模型，其公式如下：

无外部扰动的网络孤立节点系统描述为：

如果系统（1.2）被扰动时，则（1.2）就转向下面的系统：

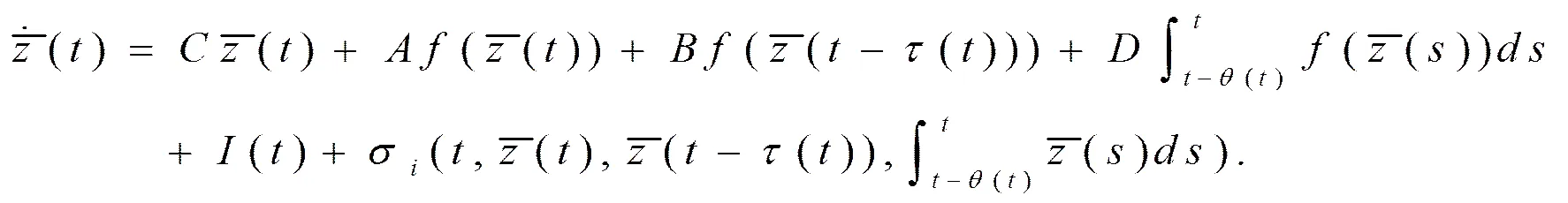
一般来说，一个系统被扰动则该系统的状态将会被改变。我们假设该系统（1.3）的状态仍是前面所提到的三种状态之一，但不一定是最初的那一种状态。

下面我们做出以下本文所需的假设必要条件：

注1.1 在其它文章中所研究的混沌系统（如：Lorenz系统、Rossler系统、混沌神经网络等）与我们所研究的网络系统（1.2）没有冲突，因此，本文的结果具有一定的通用性。

本文的目标就是证明所有形式的复杂网络（1.1）都是同步的。

就在这时，砖子和赵仙童的手机几乎同声响起，一个是小鸟叫，一个轻音乐，两人查看信息时，头颅同时伸向对方的手机，同声说，女儿发来的，老爸，你和老妈没什么问题吧？老妈，你和老爸没什么问题吧？

引理1.1（Schur 因式分解）见文[4]。

引理1.2 见文[5]。

引理1.3（Barbalat 引理）见文[6].

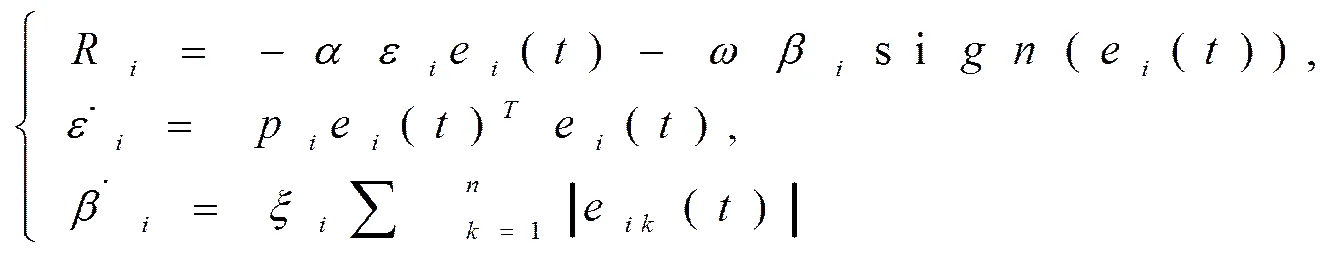
2　部分节点被扰动情况下的复杂网络同步

通常复杂网络只有部分节点被扰动的情况，如果一个网络的一些重要节点被扰动，就会使得整个网络不能正常工作，进而影响到整个网络的稳定性。理论上讲大的无定向网络或更大的定向网络的节点比小的无定向网络或更小的定向网络的节点更容易受到扰动的影响，这是由节点的状态决定的。另一方面,现实世界的复杂网络通常有大量的节点,若对网络中所有的节点都添加控制器加强稳定性,这通常是不切实际的，也是无法控制的。因此，从实践的角度和控制成本的角度出发，我们可以应用牵制控制方案（见文[1-3]）来防止外部扰动影响，实现复杂网络的同步。

在本文中，我们假设矩阵U是不可约矩阵，那么网络就不存在网络隔离集群，当第节点在外部扰动下受到影响时，为了不失一般性，我们重新组合网络节点的顺序，取第个节点进行控制，因此，针扎控制下复杂网络可以描述为：