基于点源解的偏心井试井典型曲线分析

姜瑞忠， 郜益华， 孙召勃， 何吉祥， 滕文超

( 1. 中国石油大学(华东) 石油工程学院，山东 青岛　266580；　2. 中海石油(中国)有限公司 天津分公司，天津　300452 )



基于点源解的偏心井试井典型曲线分析

姜瑞忠1， 郜益华1， 孙召勃2， 何吉祥1， 滕文超1

( 1. 中国石油大学(华东) 石油工程学院，山东 青岛266580；2. 中海石油(中国)有限公司 天津分公司，天津300452 )

直井试井一般假设井位于地层中心，在实际试井测试过程中很难保证。利用点源理论、叠加原理、镜像原理给出偏心点源解，以及外边界封闭、定压的圆形油藏中偏心井的线源解，绘制偏心井试井的典型压力曲线并分析偏心距对试井典型曲线的影响。结果表明：对于外边界封闭和定压油藏试井曲线偏心距的存在使边界响应提前出现；与井位于地层中心时的情况不同，考虑偏心距后外边界封闭油藏的边界响应可划分为封闭边界响应扩大阶段和整个封闭边界响应阶段；考虑外边界定压油藏偏心距后，边界响应体现出压力导数下降变缓特征。

偏心井； 线源解； 典型压力曲线； 偏心距； 边界响应

0　引言

目前，考虑外边界条件的圆形地层直井试井分析一般均假设井位于地层中心[1-9]。在实际试井测试中由于地层条件存在复杂性，很难出现井位于地层中心的理想情况，因此有必要对偏心井问题进行研究。Muskat M、葛家理等利用镜像反映法得到圆形地层考虑外边界条件的偏心井稳定产量公式[10-11]，刘洪等采用边界元方法研究封闭地层中偏心井的不稳定产量变化[12]，但关于偏心井不稳定试井的研究极少。

笔者采用偏心距描述偏心井在地层中的位置，利用点源理论得到外边界定压和封闭油藏中偏心井的线源解，从而得到偏心井试井问题的解析解和典型试井曲线，为偏心井试井分析提供依据。为验证模型的正确性，与刘洪等采用边界元方法所得结果[12]进行对比，并将文中的模型退化为井位于地层中心的情况，与Ozkan E给出的井位于地层中心的线源解[13]进行对比，分析偏心距对考虑外边界条件试井曲线的影响。

1　模型建立及求解

1.1物理模型

考虑单层、均质外边界封闭或定压圆形油藏中一口偏心井的情况，见图1。模型基本假设：

(1)油藏水平均质，厚度为h，外边界半径为re，开井生产前均匀分布的地层压力为pi；

(2)地层流体、岩石微可压缩，流动符合达西定律；

(3)井位于油藏内任意位置，采用偏心距ra描述井的位置；

(4)井可视为线源，以定产量q生产，且井在整个油层内射孔生产；

(5)忽略重力影响；

(6)考虑表皮因子和井筒存储效应的影响。

1.2数学模型及模型求解

在球坐标系下，偏心点源的渗流微分方程为

(1)

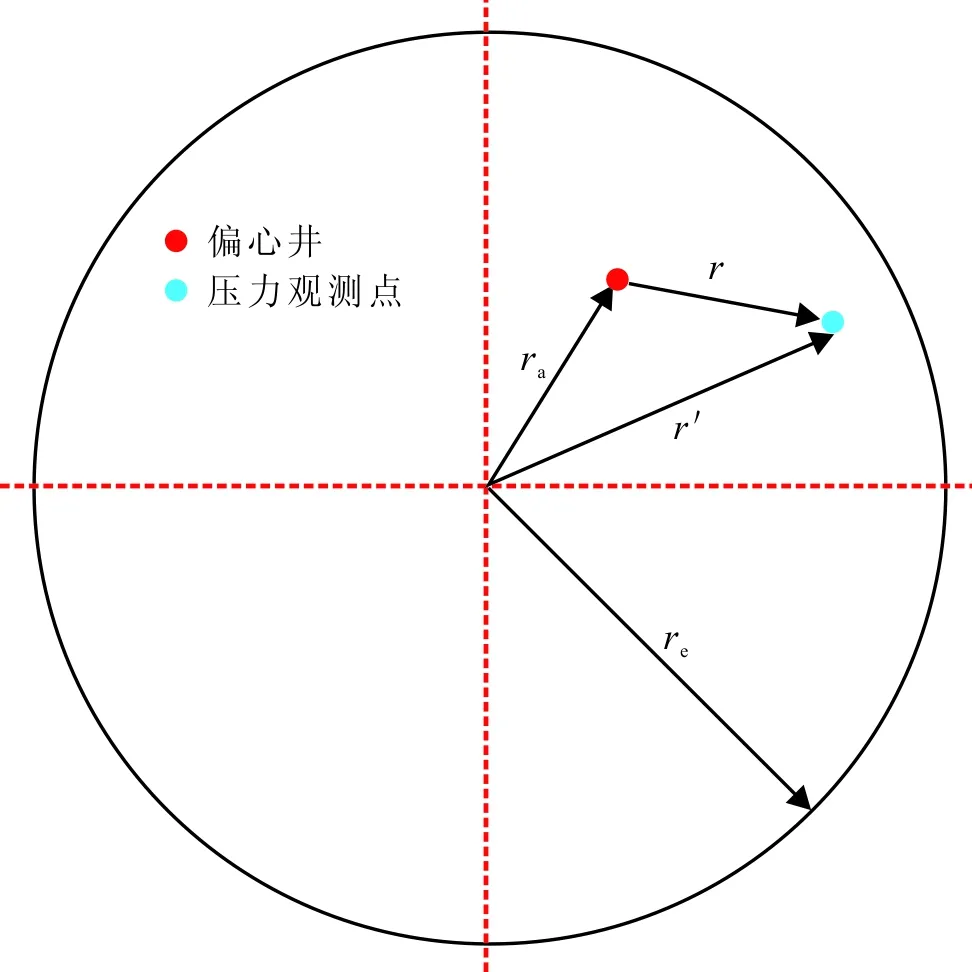
图1　外边界封闭或定压油藏偏心井示意Fig.1 Schematic diagram of eccentric well in reservoir with closed boundary or constant pressure boundary

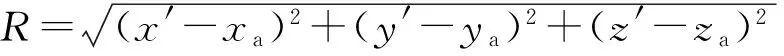
瞬时点源的内边界条件为

(2)

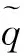
油藏初始条件为

(3)

外边界条件：

(1)定压外边界

(4)

式中：re为柱坐标系下从油藏中心计起的外边界半径。

(2)封闭外边界

(5)

顶底边界封闭

(6)

将无因次变量代入式(1-6)并进行拉普拉斯变换,拉式空间下的瞬时偏心点源模型为

(7)

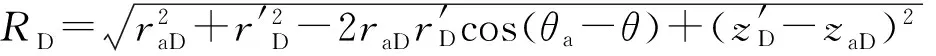
无因次瞬时点源内边界条件为

(8)

顶底边界封闭

(9)

外边界条件：

(1)定压外边界条件

(10)

(2)封闭外边界条件

(11)

式(10-11)中：reD为外边界无因次半径。

由点源理论[13-16]知，瞬时偏心点源模型对应的连续偏心点源解可写成

(12)

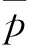
在瞬时偏心点源模型的基础上，结合叠加原理、镜像原理可得无穷大外边界的连续偏心点源解为

(13)

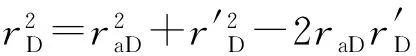
(14)

式中：Ik为k阶第一类虚宗量贝塞尔函数;Kk为k阶第二类虚宗量贝赛尔函数；a为系数。

将式(14)代入式(13)可得

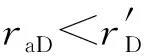
(15)

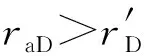
(16)

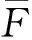
(17)

式中:ξk、ζk为待定系数。

此时，有

(18)

(1)对于封闭外边界油藏，有

(19)

(20)

(2)对于定压外边界油藏，有

(21)

(22)

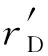
对于封闭边界油藏偏心线源解为

(23)

对于定压边界油藏偏心线源解为

(24)

当考虑井筒存储效应和表皮效应时，利用杜哈美原理[18]可得

(25)

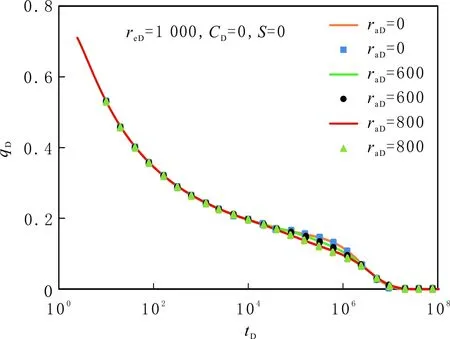
图2　封闭边界偏心井不稳定产量结果对比Fig.2 Comparison of transient rate for eccentric well in reservoir with closed boundary between Liu's study and results in this paper

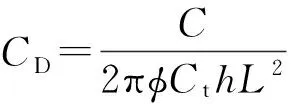
对式(25)利用Stehfest数值反演方法进行反演，即可得到真实空间的偏心井井底压力解。

2　模型验证

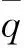
(26)

刘洪等应用边界元方法研究外边界封闭时偏心井不稳定产量变化[12]。为验证模型，利用文中模型及式(26)做出封闭边界条件下不稳定产量变化与刘洪等所得结果进行对比，见图2(实线为文中模型所得结果；点线为刘洪等利用边界元法所得结果)。

由图2知：文中得到的封闭边界偏心井不稳定产量解析解与刘洪等利用边界元方法得到的结果一致，在一定程度上验证模型的正确性。

另外，为验证模型的正确性，令模型中偏心距raD=0，做出井位于地层中心时的压力及压力导数曲线，与Ozkan E给出的井位于地层中心线源解[11]进行对比。为方便对比，将Ozkan E给出的线源位于地层中心的解[11]转化为文中给出的无因次压力形式，结果见图3和图4。

对于封闭外边界，有

(27)

对于定压外边界，有

(28)

由图3和图4知：当偏心距raD=0时，文中模型可以退化为井位于地层中心时的试井模型，两者所得结果相同，再次验证模型的正确性。

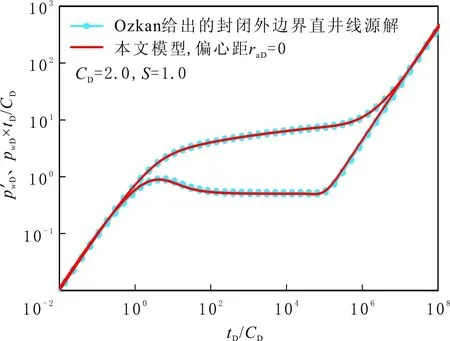
图3　封闭外边界典型压力图版对比Fig.3 Comparison of type pressure curve for reservoir with closed boundary

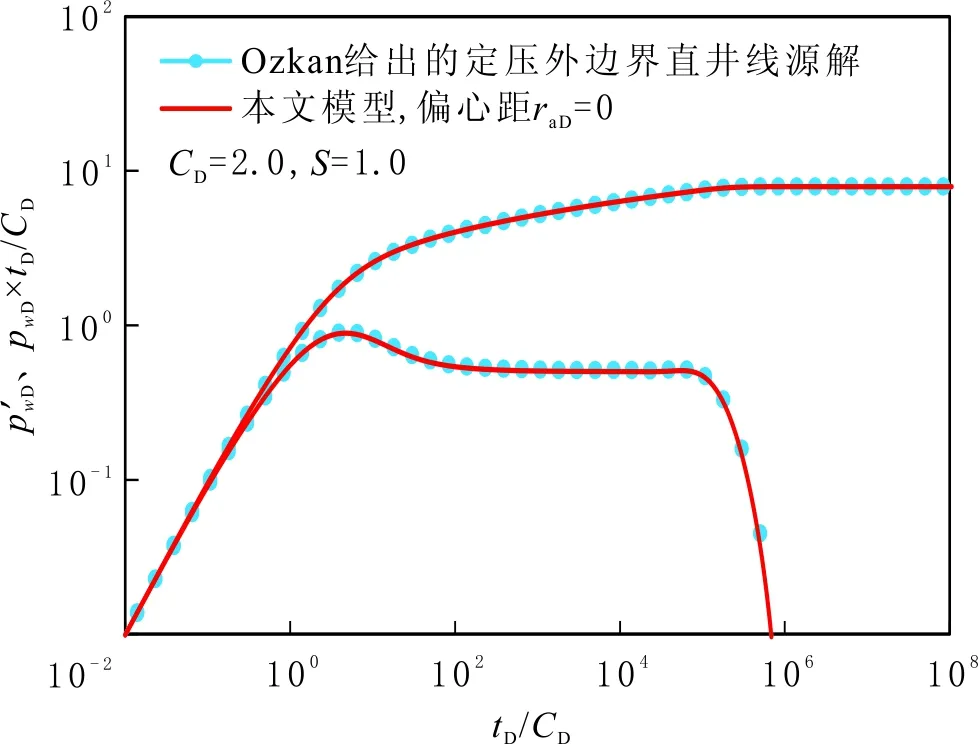
图4　定压外边界典型压力图版对比Fig.4 Comparison of type pressure curve for reservoir with constant-pressure boundary

3　压力图版分析

3.1典型图版

根据文中模型做出外边界封闭和定压时的偏心井试井典型压力曲线，并与井位于地层中心(raD=0)的典型曲线进行对比，见图5和图6。

图5分别给出封闭边界条件下不考虑偏心距(raD=0)时外边界reD=1 000、200，以及考虑偏心距raD=800，而外边界为reD=1 000时的压力及压力导数曲线。由图5可见，考虑偏心距后边界响应提前出现。另外，不考虑偏心距时封闭边界的响应特征是压力导数斜率为1，而考虑偏心距后封闭边界可分为2段：封闭边界响应扩大段，偏心井压力传播到部分边界，该阶段压力导数上升，但斜率不为1；整个封闭边界响应阶段，偏心井压力完全传到边界，该阶段压力导数斜率为1。因此，考虑偏心距后圆形封闭边界油藏直井试井的流动阶段可划分为5个阶段：(1)早期纯井筒存储阶段；(2)过渡阶段；(3)径向流阶段；(4)封闭边界响应扩大阶段；(5)整个封闭边界响应阶段。

图6分别给出定压边界条件下不考虑偏心距(raD=0)时外边界reD=1 000、200，以及考虑偏心距raD=800而外边界为reD=1 000时的压力及压力导数曲线。由图6可见，考虑偏心距的主要影响体现在边界反映阶段，偏心距后边界响应提前出现。另外，考虑偏心距后边界响应特征也明显不同，对于定压边界，边界响应的特征为压力导数下降，不考虑偏心距时不同外边界半径下的边界响应基本平行，而考虑偏心距后压力导数的下降变缓，压力下降速率最后趋于相同。与封闭边界不同，定压边界油藏考虑偏心距后其边界响应没有明显分界线，流动阶段划分4个阶段：(1)早期纯井筒存储阶段；(2)过渡阶段；(3)径向流阶段；(4)定压边界反映阶段，在偏心距的影响下压力导数下降变缓。

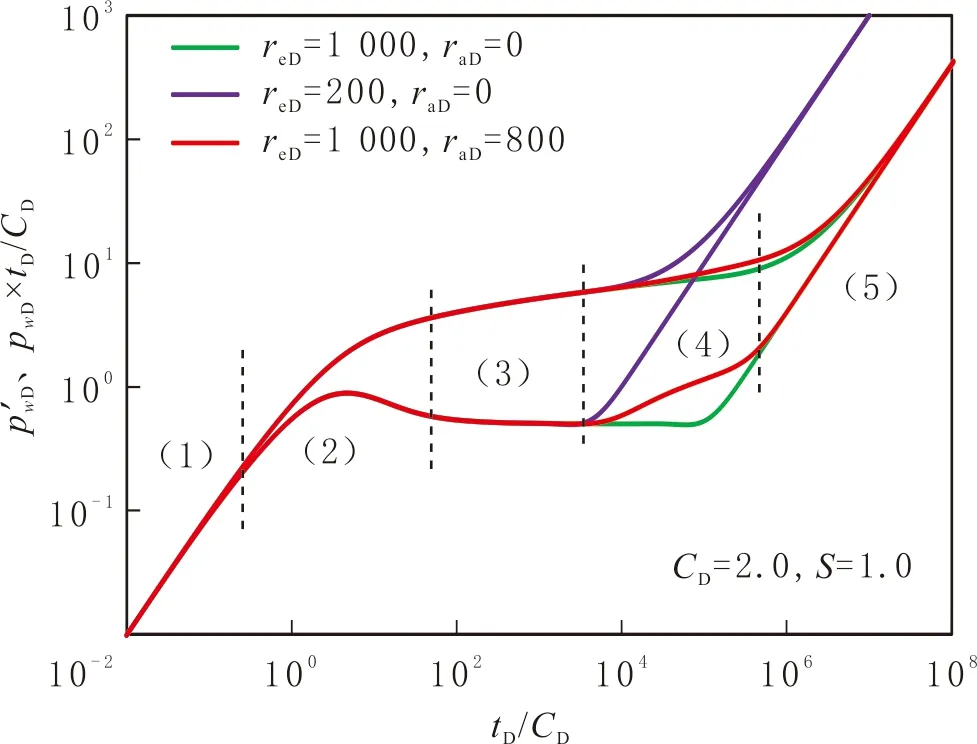
图5　封闭边界下偏心井典型压力图版Fig.5 Type pressure curve of eccentric well in reservoir with closed outer boundary

图6　定压边界下偏心井典型压力图版Fig.6 Type pressure curve of eccentric well in reservoir with constant pressure outer boundary

3.2参数敏感性

为研究偏心距对外边界封闭或定压油藏试井曲线的影响，绘制不同偏心距下的典型压力图版，见图7和图8。

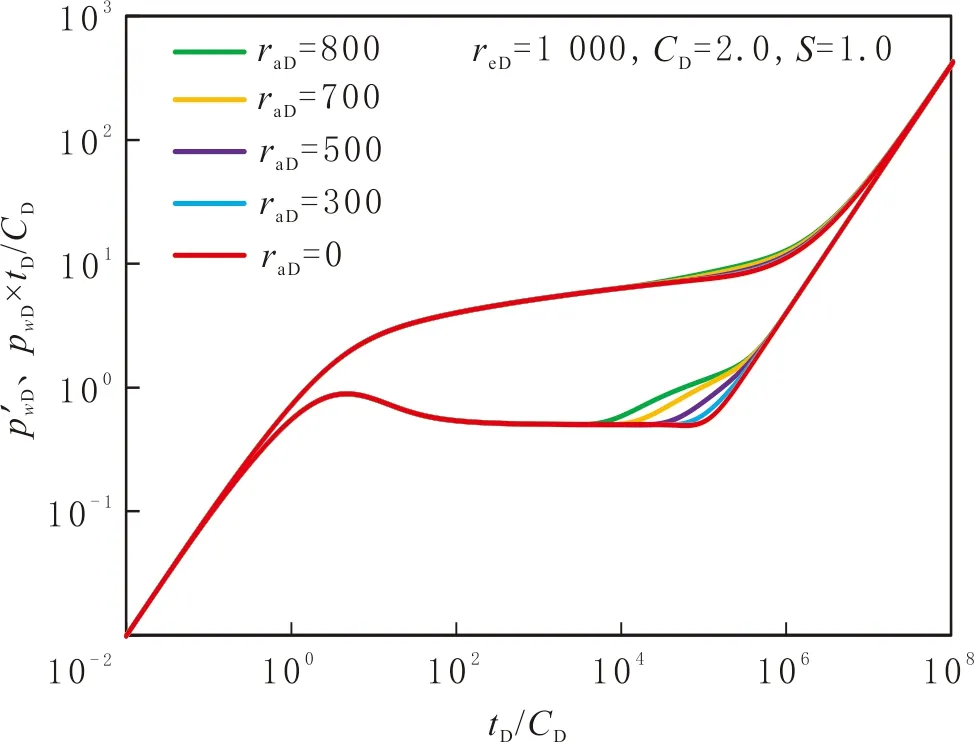
图7　偏心距对封闭边界油藏的影响Fig.7 Effect of offset distance on the pressure curve for eccentric well in reservoir with closed boundary

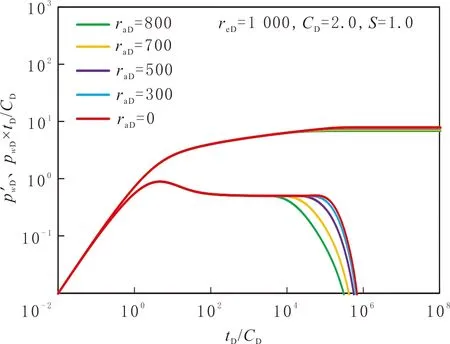
图8　偏心距对定压边界油藏的影响Fig.8 Effect of offset distance on the pressure curve for eccentric well in reservoir with constant pressure boundary

由图7可知，偏心距越大，边界响应开始的越早，封闭边界响应扩大段越长，该阶段压力导数的斜率越小。这是因为偏心距越大，直井距外边界的最小距离越小，压力开始传播到边界的时间越短，边界响应开始的时间越早；同时，偏心距增大，导致压力完全传播到边界的时间变晚，边界响应早期压力导数的斜率越小。

由图8可知，偏心距越大，边界响应出现越早，压力导数曲线下降越缓。这是因为考虑偏心距后，压力传播到边界的时间不同，偏心距越大，压力开始传播到边界的时间越早，边界响应出现越早；同时，偏心距越大，压力完全传播到边界的时间越晚，边界响应早期压力导数的下降越缓。

4　实例解释

某油田对一直井测得300 h的压力下降数据，见图9。该井的试井数据表现出偏心井特征，采用文中模型得到很好的拟合效果。经解释，该井的外边界半径约为255 m，偏心距约为45 m，渗透率约为150×10-3μm2。

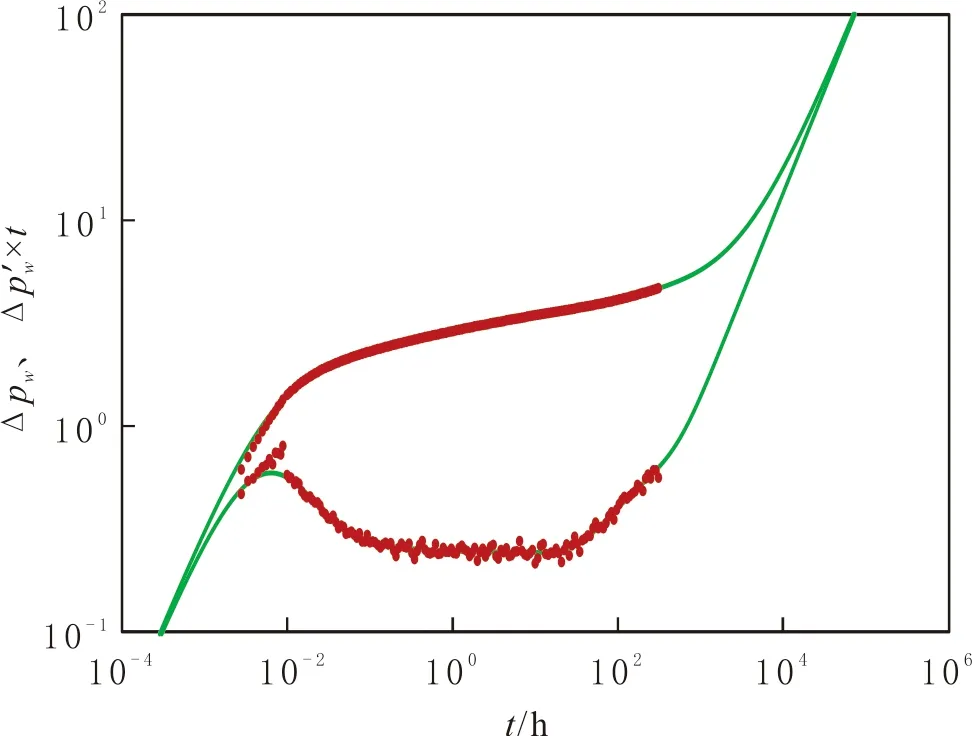
图9　某封闭边界偏心井拟合结果Fig.9 Matching result of a closed boundary eccentric well

5　结论

(1)在点源理论基础上得到偏心井试井模型的解析解，并通过与刘洪、Ozkan E等的研究结果进行对比，验证模型的正确性。

(2)对于封闭外边界油藏，偏心距使边界响应分为2段：封闭边界响应扩大段，偏心井压力传播到部分边界，压力导数上升，但斜率不为1；整个封闭边界响应阶段，偏心井压力完全传播到边界，压力导数斜率为1。

(3)对于定压外边界油藏，考虑偏心距后边界响应并没有明显的分界线。偏心距越大，边界响应出现越早，边界响应阶段压力导数曲线下降越缓。

[1]张璋,何顺利.变形介质储层压力恢复试井曲线特征[J].重庆大学学报,2013,36(11):108-114.

Zhang Zhang, He Shunli. Pressure buildup behavior in deformable medium formation [J]. Journal of Chongqing University, 2013,36(11):108-114.

[2]张林,贾永禄,张福洋,等.考虑二次压力梯度非线性渗流三区复合油藏模型分析[J].大庆石油学院学报,2011,35(5):54-59.

Zhang Lin, Jia Yonglu, Zhang Fuyang, et al. Analysis of considering quadratic pressure gradient nonlinear percolation in 3-zone composite reservoir [J]. Journal of Daqing Petroleum Institute, 2011,35(5):54-59.

[3]陈方方,贾永禄,霍进,等.三孔介质径向复合油藏模型与试井样板曲线[J].大庆石油学院学报,2008,32(6):64-67.

Chen Fangfang, Jia Yonglu, Huo Jin, et al. The flow model of the triple-medium composite reservoirs and the type curves [J]. Journal of Daqing Petroleum Institute, 2008,32(6):64-67.

[4]姚军,刘顺.基于动态渗透率效应的低渗透油藏试井解释模型[J].石油学报,2009,30(3):430-433.

Yao Jun, Liu Shun. Well test interpretation model based on mutative permeability effects for low-permeability reservoir [J]. Acta Petrolei Sinica, 2009,30(3):430-433.

[5]杨志刚,陈玉祥,王霞.考虑外边界影响的多层复合油藏试井解释数学模型[J].石油化工应用,2011,30(3):16-19.

Yang Zhigang, Chen Yuxiang, Wang Xia. Logging interpretation mathematical model of multi-bed composite reservoir considering the influence of boundary [J]. Petrochemical Industry Application, 2011,30(3):16-19.

[6]贾永禄.外边界定压试井分析有效井径模型及其样版曲线[J].西南石油学院学报,1993,15(4):51-57.

Jia Yonglu. Effective wellbore radius model with constant pressure at external boundary and its type-curves in well test analysis [J]. Journal of Southwestern Petroleum Institute, 1993,15(4):51-57.

[7]刘泽俊,孙智,宋考平.有界地层非牛顿渗流试井解释模型[J].大庆石油地质与开发,1996,15(3):63-66.

Liu Zejun, Sun Zhi, Song Kaoping. Interpretive models for non-newtonian seepage flow well testing in bounded formations [J]. Petroleum Geology & Oilfield Development in Daqing, 1996,15(3):63-66.

[8]胡建国.圆形定压边界油藏试井分析方法[J].中国海上油气:地质,1997,11(5):51-59.

Hu Jianguo. Method of well-test analysis for a circular reservoir with constant-pressure outer boundary [J]. China Offshore Oil and Gas: Geology, 1997,11(5):51-59.

[9]廖新维,沈平平.现代试井分析[M].北京:石油工业出版社,2002:122-124.

Liao Xinwei, Shen Pingping. Modern well test analysis [M]. Beijing: Petroleum Industry Press, 2002:122-124.

[10]Muskat M. The flow of homogeneous fluids through porous media [M]. Boston: International Human Resources Development Corporation, 1982:169-175.

[11]葛家理,宁正福,刘月田,等.现代油藏渗流力学原理[M].北京:石油工业出版社,2000:89-90.

Ge Jiali, Ning Zhengfu, Liu Yuetian, et al. The modern mechanics of fluids flow in oil [M]. Beijing: Petroleum Industry Press, 2000:89-90.

[12]刘洪,王新海,任路,等.偏心井产量变化规律研究[J].数值计算与计算机应用,2012,33(3):159-166.

Liu Hong, Wang Haixin, Ren Lu, et al. Production change rules of eccentric well [J]. Journal on Numerical Methods and Computer Applications, 2012,33(3):159-166.

[13]Ozkan E. Performance of horizontal wells [D]. Oklahoma: The University of Tulsa, 1988:22-26.

[14]Ozkan E. New solutions for well-test-analysis problems: Part Ⅲ-additional algorithms [C]. SPE 28424, 1994.

[15]Ozkan E, Raghavan R. New solutions for well-test-analysis problems: Part 1-analytical considerations [J]. Society of Petroleum Engineers, 1991,6(3):359-368.

[16]Gringarten A C, Ramey H J. The use of source and Green's function in solving unsteady-flow problems in reservoirs [J]. Society of Petroleum Engineers Journal, 1973,13(5):285-296.

[17]Carslaw H S, Jaeger J C. Conduction of heat in solids [M]. 2nd ed. London: Oxford University Press, 1959:376-378.

[18]Kuchuk F. Generalized transient pressure solutions with wellbore storage [G]. Society of Petroleum Engineers, 1986.

[19]Van-Everdingen A F, Hurst W. The application of the Laplace transformation to flow problem in reservoirs [J]. Journal of Petroleum Technology, 1949,1(12):305-324.

2016-02-29；编辑：关开澄

国家自然基金项目(51374227,51574265)；国家科技重大专项(2016ZX05027004-004)。

姜瑞忠(1964-)，男，博士，教授，博士生导师，主要从事油气田开发方面的研究。

10.3969/j.issn.2095-4107.2016.04.010

TE353

A

2095-4107(2016)04-0080-08