公私伙伴关系中风险分担的最适比率研究
2016-10-13张阿迪沈江
张阿迪,沈江
公私伙伴关系中风险分担的最适比率研究
张阿迪,沈江
(天津大学管理与经济学部,天津300072)
随着我国经济的发展,公私伙伴关系(PPP)项目日益流行和普遍。本文首先列出了政府和机构对公私伙伴关系(PPP)的多种定义,之后介绍了实践中最常用的四种公私伙伴关系形式。其次,本文将通过有效边界和无差异曲线证明风险分担最适比率的存在。同时,在马科维茨模型的基础上建立风险分担模型,并通过拉格朗日乘数法得到这一模型的解。最后,将此模型应用到一个实际案例——广东奥林匹克体育中心中,展示该风险分担模型的实用性和有效性。
公私伙伴关系(PPP);马科维茨模型;风险分担模型;拉格朗日乘数法
一、引言
我国是世界上发展最快的国家之一,其基础设施投资领域前景光明。但由于政府在资源分配和项目融资中扮演主导角色,因此存在广泛的风险。根据学者Wilkins和Zurawski的研究表明,“中国约85%的基础设施投资由国家主导,远远高于其它国家的一般比例。由于缺乏完善的项目优先排序框架和透明的成本效益分析,只能高度依赖政府主导的投资,造成了无效投资和资源分配不当的可能性”①。我国已经就解决政府融资相关问题提出了多种改革措施,其中之一就是提高私人投资基础设施的比例。由此,公私伙伴关系(PPP)项目无疑将更加流行和普遍。
由于PPP建设项目的特殊性,此类项目存在巨大风险,因此需要特别注意[1]。尤其是在我国,PPP项目刚刚起步,相关的市场机制和行业标准尚未成熟,存在诸多不确定因素。因此,对风险分担问题进行分析有助于增强承包商对此类项目交付体系的信心,激励承包商予以尝试,缓解政府的财政压力。
基于这一目标,本文首先对PPP进行定义,并比较世界各地对PPP的不同定义方法和多种PPP形式。其次,将利用有效边界和无差异曲线展示风险分担最适比率的存在。通过使用基于马科维茨均值-方差组合模型的二维规划法,将建立适用于我国的风险分担模型。最后,将此模型应用到一个实际案例-广东奥林匹克体育中心中,将利用拉格朗日乘数法等数学方法寻找不同模型场景的解,实现风险分担边界的有效组合,从而使每一特定风险水平范围内的各种组合实现效益最大化,或在某些情况下实现收益风险最小化,进而展示该风险分担模型的实用性和有效性。
二、公私伙伴关系的相关理论
(一)公私伙伴关系的定义
总体而言,公私伙伴关系(PPP)是指私营部门与公共政府在公共基础设施的融资、设计、施工和运营中产生相关联的项目。由于PPP本身的复杂性和政府希望与私营部门合作采取的形式不同,世界上存在多种对PPP的定义。
美国公私伙伴关系全国理事会(National Council for Public-Private Partnership)认为PPP是公共机构与盈利性私营开发者之间的一种契约安排,通过这一安排,双方共享资源、分担风险,从而提供公共服务或开发公共基础设施[2]。
加拿大公私伙伴关系国家委员会(Council for Public–Private Partnerships)认为PPP是公共部门和私人部门之间的一种合作经营关系,它建立在双方各自经验的基础上,通过适当的资源分配、风险分担和利益共享机制,最好地满足事先清晰界定的公共需求[3]。
欧洲投资银行(European Investment Bank)甚至将PPP扩展到非正式层面[4],指出“公私伙伴关系是对私营部门与公共机构为向私营部门引入资源和/或专业技能而建立的关系的通称,目的是向公共部门提供资产和服务。因此,PPP一词可用于描述多种广泛的工作安排,包括宽松的、非正式的和战略性的伙伴关系,设计、建造、融资和运营(DBFO)类型的服务合同,以及正式的合资公司”。
(二)PPP的形式
在实践中,PPP的形式多种多样。
1、BOT(建设-运营-移交)
通过招投标,政府就某一个公共项目向私营部门发放特许经营权,允许私营部门在特许经营期内对项目进行融资、建设和运营,并通过相应的产品和服务获得利润。一般情况下,政府有权对该项服务和产品的数量和价格进行调整,以平衡私营部门和公共部门之间的利润,例如电厂。特许经营期末,私营部门将该项目移交给政府。
2、BT(建设-移交)
BT与BOT类似,但不包括运营的过程。私营部门只负责融资和建设。项目竣工后,私营部门应将项目移交给政府。作为回报,政府应按合同规定支付相应费用。在美国该种形式本质上是一次性付款,除了项目的性质为公共项目。
3、TOT(移交-经营-移交)
政府将一个完整项目的全部或部分所有权或特许权移交给私营部门,获得相应补偿。私营部门通过运营该项目收回投资、获得利润。特许经营期末,私营部门将项目归还政府,不获得任何补偿。
4、TBT(移交-建设-移交)
TBT是BOT和TOT形式的组合。从政府的角度出发,通过采用TBT,TOT的实施仅扮演辅助作用,协助BOT的实施。总体而言,政府将已竣工项目和待施工项目打包,之后将特许经营权移交给私营部门。
三、基于马科维茨理论的风险分担模型
(一)马科维茨投资组合理论介绍
马科维茨将风险定义为投资收益率的分散程度。分散程度越高,风险越大[5]。标准差和方差可以用来描述分散程度。此外,马科维茨认为股票组合的风险不仅与每支股票的风险有关,还与各支股票之间的相互关系有关。这种相互关系可以用协方差表示。以所有投资者都是理性的经济人这一假设为基础,马科维茨认为所有投资者都在寻求最低风险下的一定利润,或者在一定风险下实现利润最大化。之后马科维茨将二维平面图法应用到马科维茨均值-方差模型。通过这一模型,可以得到有效边界,该有效边界上的任意组合都可以满足理性经济人的要求[6]。
本文将马科维茨理论应用到风险分担模型中。预期收益率能够反映特定风险承担者承担该风险获得的利润,之后又利用预期收益率的波动性衡量每位风险承担者的风险。换言之,预期收益率的方差越高,波动性越大,风险越高,风险承担者控制该风险的能力越低。本文基于马科维茨均值-方差模型得到了风险分担的有效边界。也就是说,在承担一定风险的情况下,该比率能够实现最高的预期收益率;在实现同样收益率的情况下,该比率承担的风险最低。
(二)建立风险分担模型,确定最适比率
在此基础上能够建立两个模型:
四、案例研究:以广东奥林匹克体育中心为例
根据前述内容所示,本文证明了风险分担的最适比率确实存在,之后为PPP项目建立了风险分担模型。本部分将讨论如何将该风险分担模型应用到实际案例中。
(一)广东奥林匹克体育中心的背景
为举办第九届全国运动会,深圳市政府携手万科集团建造了一座现代化的多用途体育场,占地面积101万平方米。施工单位是中国建筑工程总公司。为方便分析,本文仅考虑三方分担风险。实践中,风险承担方的数量应大于三。
(二)数据选择及处理
由于政府考虑更多的是社会效益而非经济效益,所以很难找到某一种指标来衡量政府的收益率。依据“垃圾处理PPP项目投资结构的设计研究”,本文利用十年期债券收益率作为政府投资的基准[7]。由于债券收益以年为衡量单位,本文采用万科集团和中国建筑工程总公司(CSCEC)所发布年报中的净资产收益率(ROE)与其进行比较。具体见表1。

表1:万科集团、中国建筑工程总公司和政府的历史收益率
将所有数据输入到SPSS软件后,可以得到预期收益率、收益率方差以及三方风险承担者的收益率协方差。具体见表2和表3所示。

表2:万科、CSCEC和政府的预期收益率及方差

表3:万科、CSCEC和政府的协方差
(三)建立风险分担模型
(四)模型解答
本文使用拉格朗日乘数法建立了拉格朗日函数:
上述方程组中,存在五个未知数和五个方程,所以能够得到唯一解,将这些值代入以下方程式,可以得到最低风险。
以下方程组是该模型的限制条件:
目前,本文能够得到的定义域是以下三个方程的交集。
所以,解的下限应该是0。
(五)迭代法
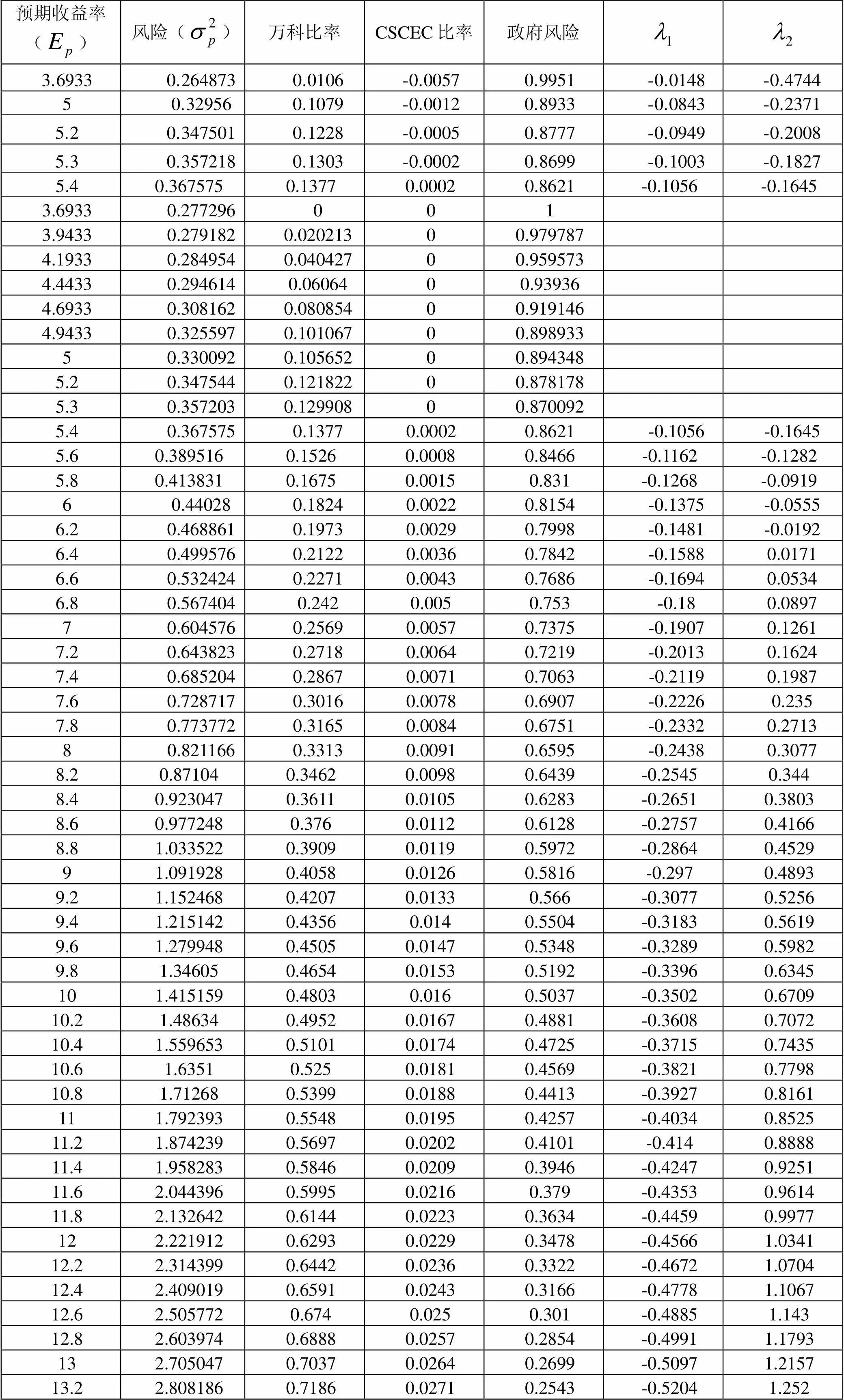
表4:一定预期收益率和风险分担比率下的最低风险
图1:表4对应的散点图

在该有效边界上万科、CSCEC和政府各自应承担风险所占百分比见图2所示。
图2:不同预期收益率下万科、CSCEC和政府的风险分担比率

根据用无差异曲线表示的最终决策者的风险偏好,决策者可以选择该条线上的一个最适比率来分担风险。必须指出的是,不存在绝对的最适比率,只有相对最适或合适的比率。
五、结论
随着经济发展,公私伙伴关系(PPP)项目日益流行和普遍。但与传统融资模式相反,PPP在一定程度上属于新兴事物。公共部门与私人部门之间合理的风险分担是PPP项目成功的关键。
本文仅是对寻求公私伙伴关系中风险分担最适比率的一次尝试。考虑到选取数据的困难性,文中所建立的模型可能并非百分之百与现实世界相匹配。本文希望通过数学方式提供一种新的衡量风险与分担风险的方法。希望本文能够激励建筑业建立相应的统计体系,便于未来分担风险时对风险进行衡量。
[注释]
① 参见:《澳洲联储公告》中Wilkins k和Zurawski A“基础设施投资在中国”一文,2014年第27-36页。
[1] 陈菲,王晓腾.基础设施公私伙伴关系(PPP)项目中的风险分配[J].建筑经济,2008(4):31-35.
[2] LI B,AKINTOYE A.Public-Private Partnerships:Principles of Policy and Finance[M].Oxford:Butterworth Heinemann,2003:1-30.
[3] 沈汤林,程向杰.建筑业公私伙伴关系项目研究述评[J].国际项目管理,2010,28(7):683-694.
[4] 陈建伟,陈龙.欧洲投资银行(EIB)在公私伙伴关系(PPPs)中的角色[EB/OL].(2015-11-12)[2016-07-16].http://www.eib.org/infocentre/publications/all/the-eibs-role-in-public-private-partners hips-ppps.htm.
[5] MARKOWITZ H.投资组合选择[J].金融杂志,1952,7(1):77-91.
[6] 平狄克.微观经济学(第八版)[M].北京:中国人民大学出版社,2013:230-272.
[7] 刘峥.垃圾处理PPP项目投资结构的设计研究[M].北京:清华大学,2011:312-320.
Research on Optimal Ratio of Risk Sharing for Public Private Partnership
ZHANG A’DI, SHEN JIANG
The public private partnership (PPP) projects become increasingly popular as the economic development of China. Firstly, this paper lists a variety of definition of PPP from government and institutions, then demonstrates four most popular forms of PPP in practice. Next, the paper proves the existence of the optimal ratio of risk sharing through efficient frontier and indifference curve. Also the paper builds a risk-sharing model based on the Markowitz model and solves it through the Lagrange multiplier method. Finally, this paper applies the model to solve the practical problem of Guangdong Olympic Sports Center, demonstrating the usefulness and effectiveness of the risk sharing model.
Public Private Partnership; Markowitz Model; Risk Sharing Model; Lagrange Multiplier Method
F062
A
1008-472X(2016)06-0013-10
2016-10-08
国家自然科学基金项目(71171143)
张阿迪(1977-),女,辽宁沈阳人,天津大学管理与经济学部博士研究生,研究方向:项目管理;
沈 江(1951-),男,天津人,天津大学管理与经济学部教授、博士生导师,研究方向:项目管理。
本文推荐专家:
吴晓宇,南开大学商学院,教授,研究方向:项目管理。
马建林,天津大学管理与经济学部,教授,研究方向:项目管理。
