具有孔道沉槽的滑阀过流面积分析

张立杰　王力航　王　帅　李德新

1.燕山大学河北省重型机械流体动力传输与控制重点实验室，秦皇岛，0660042.先进锻压成形技术与科学教育部重点实验室，秦皇岛，066004



具有孔道沉槽的滑阀过流面积分析

张立杰1,2王力航1王帅1李德新1

1.燕山大学河北省重型机械流体动力传输与控制重点实验室，秦皇岛，0660042.先进锻压成形技术与科学教育部重点实验室，秦皇岛，066004

多路阀以其高集成度被广泛应用于工程机械领域，其中阀口形式对多路阀流量控制特性具有重要影响。对于阀体上开有孔道沉槽、节流面为常见的圆柱面和圆锥面两种滑阀阀口形式的多路阀，根据其结构特征及内部流场压力分布和速度变化情况，利用等效阀口面积理论，推导了圆柱面阀口和圆锥面阀口过流面积计算公式。利用流场仿真对计算结果进行了修正，采用实验手段验证了计算结果的准确性。研究结果对滑阀阀芯的多路阀设计及性能预测具有一定参考价值。

多路阀；孔道沉槽；阀口过流面积；流场仿真

0　引言

工程机械液压系统中，多路阀依靠滑阀阀芯凸肩限制液流的流量，从而控制执行机构的运动速度、方向等。滑阀因结构形式多、控制性能良好，在液压阀中有着广泛应用[1]。按照不同标准,滑阀存在多种分类方法[2]，其中，按阀体窗口形状划分，滑阀可分为矩形窗口、圆形窗口、三角形窗口等，矩形窗口又可分为全周开口型阀口和非全周开口型阀口。多路阀中广泛采用的阀口节流槽结构(如U形、V形、K形及其组合等)多属于矩形窗口非全周开口形式，对于这种结构形式，文献[3-4]在节流槽滑阀阀芯过流面积计算、稳态液动力特性及气穴噪声特性等方面展开了较为系统的研究。另一方面，圆形窗口形式滑阀以其优良的工艺特性在多路阀中也有较多应用。

本文提出了一种带有孔道沉槽结构且阀芯凸肩为圆柱面和圆锥面两种形式的圆形窗口滑阀阀口过流面积的计算方法。孔道沉槽是指加工在阀孔对侧，且与窗口相同直径的沉槽，孔道沉槽结构可有效提高圆形窗口的通流能力。本文针对圆柱面与圆锥面两类滑阀阀芯凸肩结构特征，应用等效阀口面积理论，推导阀口过流面积随阀口开度的函数关系并利用流场仿真和实验手段对计算结果进行修正和验证。

1　圆形窗口滑阀阀口过流面积分析

1.1圆柱面阀芯凸肩过流面积分析

采用圆柱面阀芯凸肩与圆柱形孔道形成部分柱面的阀口一般应用于微动特性要求不严格且大流量的多路阀中，在不增大滑阀阀杆尺寸的前提下，可采用在阀体上加工孔道沉槽的方法来增大阀口流量，结构示意图见图1。液压油流经上下两个节流面到达出油口，则阀口过流面积由上下两个部分组成，分别为：出油孔道(圆柱面2)、阀芯移动孔道(圆柱面1)及阀芯凸肩所围成相贯面面积和孔道沉槽(圆柱面3)与阀芯移动孔道柱面(圆柱面1)及阀芯凸肩所围成的相贯面面积。这两部分面积上下结构对称，面积相等，计两部分面积总和为A1。

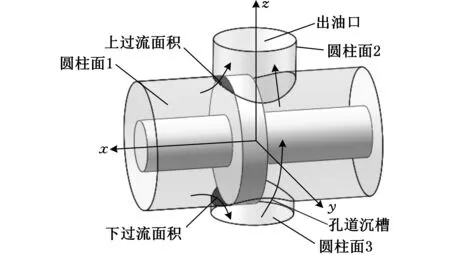
图1　圆柱面阀芯凸肩滑阀结构示意图

由于上下通流面积对称，故可先对上过流面积的二分之一进行求解。阀口计算面积简图见图2，建立图示坐标系，坐标原点位于阀芯轴线与通油孔轴线的交点。

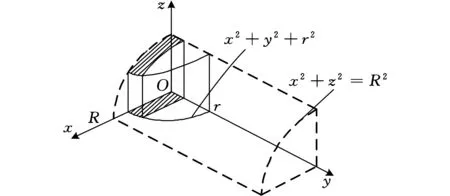
(a)正交圆柱相贯面计算简图

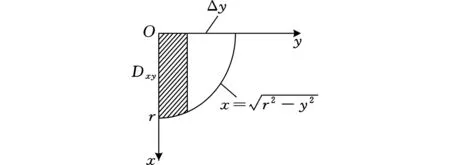
(b)计算二重积分定义域图2　圆柱面阀口面积计算简图

图2中，R为阀芯凸肩半径，r为阀体通油孔道半径，Δy为阀口开度，为了方便计算，取图2a中阴影部分面积Aq表示阀口过流面积在相贯面上的互补面积。由图2a可得阀芯移动通道柱面方程为

x2+z2=R2

(1)

通流孔道柱面方程为

x2+y2=r2

(2)

图2b为上过流面互补面在xOy面上的投影区域Dxy，可得其定义域为

利用曲面积分公式，可求得图2a中的曲面阴影面积：

(3)

代入定义域Dxy可得曲面阴影面积随开度Δy变化的计算公式：

(4)

则阀口逐渐开启时整个阀口过流面积A1(Δy)可表示为

A1(Δy)=2×2×(Aq(0)-Aq(Δy))=

(5)

1.2圆锥面阀芯凸肩过流面积分析

圆锥面阀芯凸肩是指在阀芯轴肩上加工出具有一定坡度的环面，这种阀芯凸肩与阀体形成圆锥面阀口。通过合理设计不同的环面坡度和锥形长度，可以提高液压系统在小开口处的可控性，获得丰富的多级阀口面积曲线，实现对流量的多级节流控制，进而根据不同工况分级控制执行机构的速度，且能满足不同工况下执行机构启动或停止时的平稳性要求，图3为圆锥面阀口结构示意图。

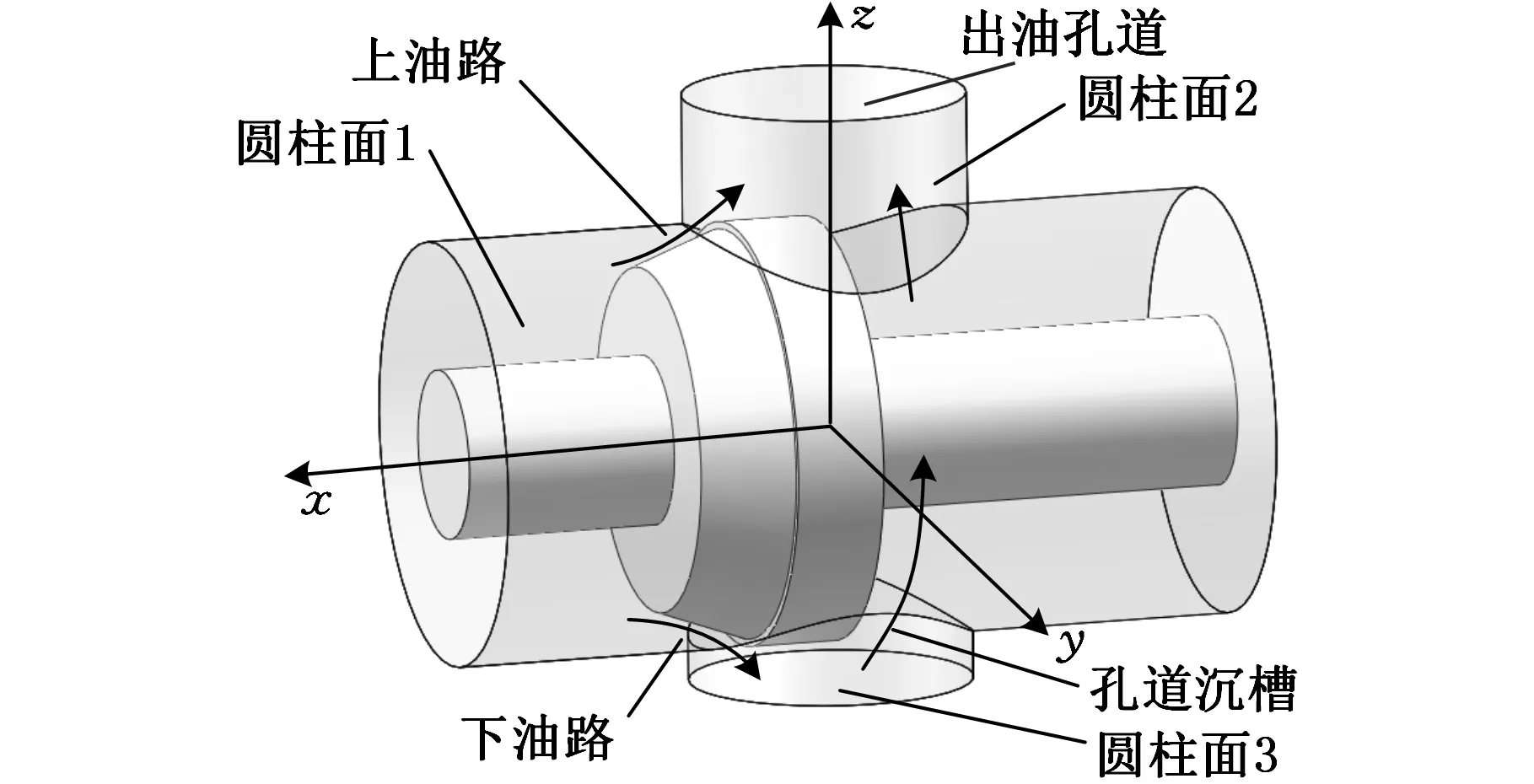
图3　圆锥面阀芯凸肩滑阀结构示意图

对于圆锥面阀口面积的计算，引入等效阀口面积的概念[3]。等效阀口面积是把复杂阀口流道中具有明显节流作用的地方等效为一个薄壁孔口。图4为圆锥面阀口在某开度下阀腔内的压力分布云图，可以看出阀口压差主要集中在相贯面A1及部分环面A2上，当阀口开度变化时，A1和A2随之变化，压差分配也会发生变化。

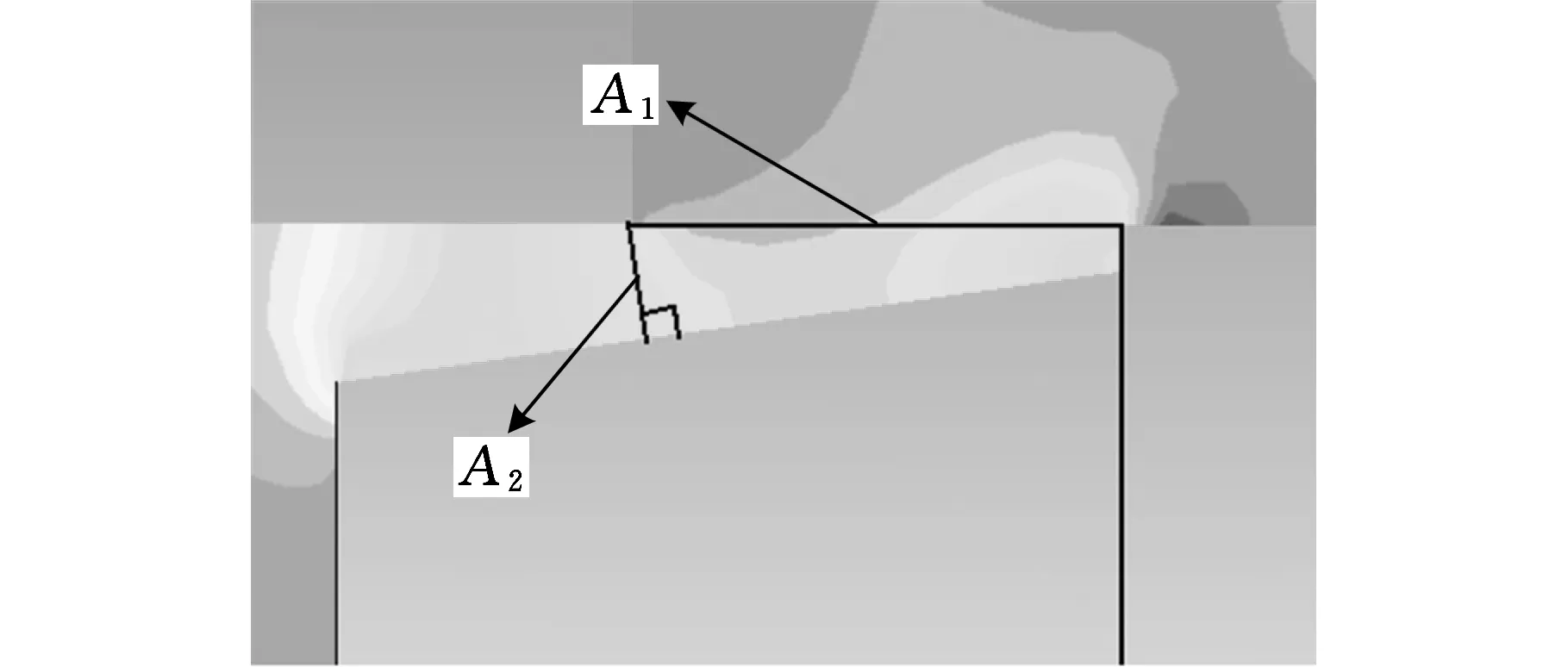
图4　圆锥面阀口压力分布云图

因此，圆锥面阀口面积可以按照A1和A2两个等效阀口面积串联阀口来计算，如图5所示。

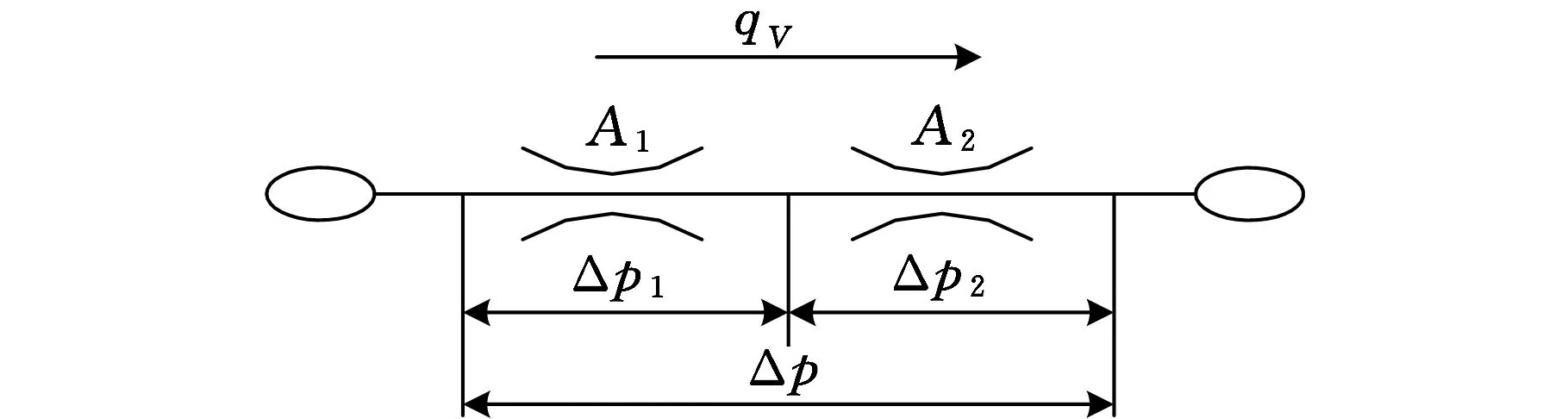
图5　阀口串联原理图

流量方程为

(6)

式中，qV为通过节流口A1、A2的流量；Cdi(i=1,2)为节流口Ai的流量系数；Cd为A1、A2串联等效流量系数；ρ为油液密度。

则压力方程为

Δp=Δp1+Δp2

(7)

取Cd=Cd1=Cd2，得

(8)

其中，A1为圆柱面1与圆柱面2的相贯面面积和圆柱面1与圆柱面3的相贯面面积之和，可利用式(6)求得。

A2为阀芯轴线与出油孔道轴线公共平面内，阀芯孔道与出油孔道交点P到锥面垂线绕阀芯轴线旋转而成的面与相贯面长度相对应的部分圆台侧面积，如图6a所示。阀口结构参数如图6b所示，其中，R为阀芯半径、r为阀体出油口半径、Δy为阀口开度、L为阀口开度对应的弦长、θ为弦长对应的夹角。

由图6b可得

(9)

(10)

图7为环面计算示意图，其结构参数ΔR为阀芯凸肩到锥面底部距离、α为圆锥半锥角、d为圆台母线、R1为圆台上平台半径。

圆台母线表达式为

(11)

圆台上平台半径为

R1=R-dcosα

(12)

圆台侧面积AL可表示为

AL(Δy)=π[R+(R-dcosα)]d

(13)

则部分环面A2(含上下两部分)可表达为

(14)

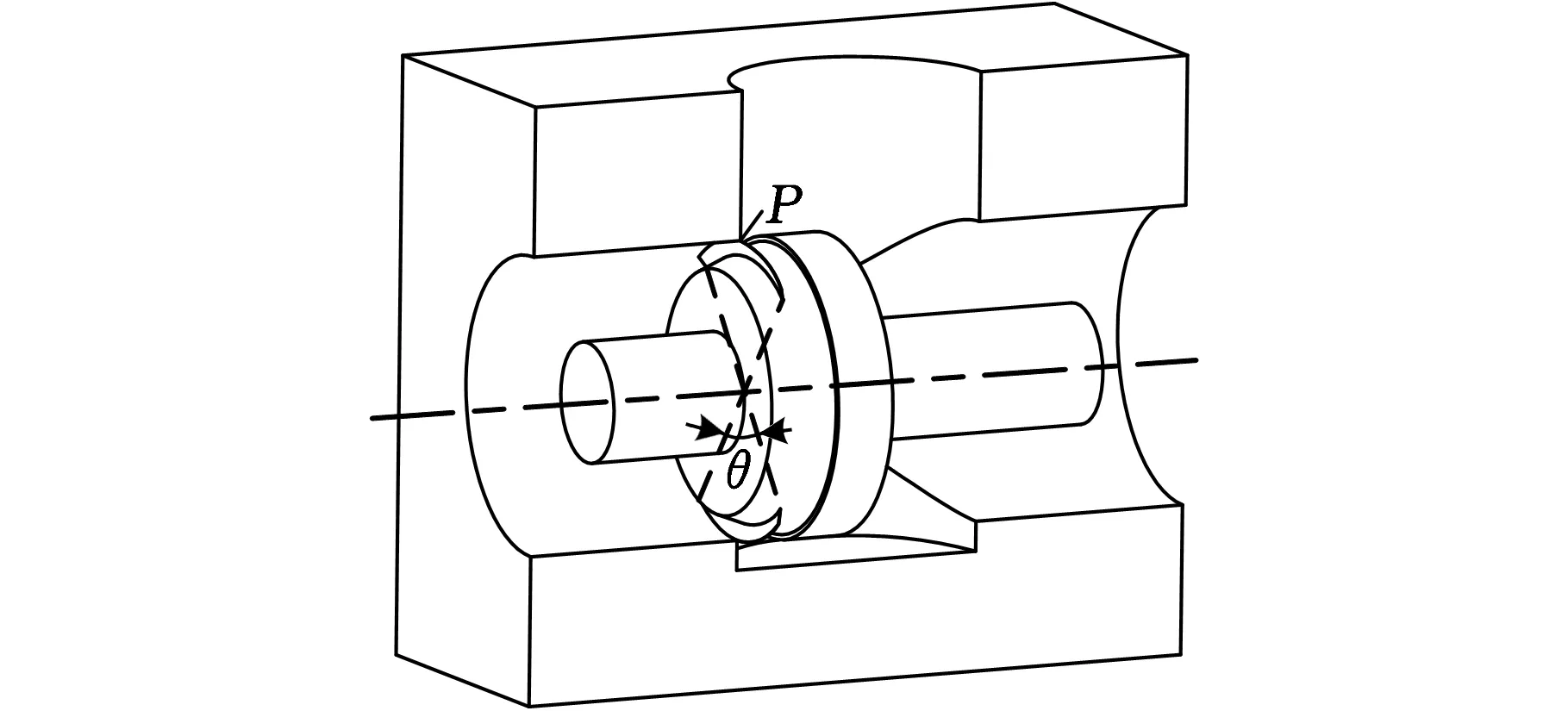
(a)部分锥面结构三维示意图

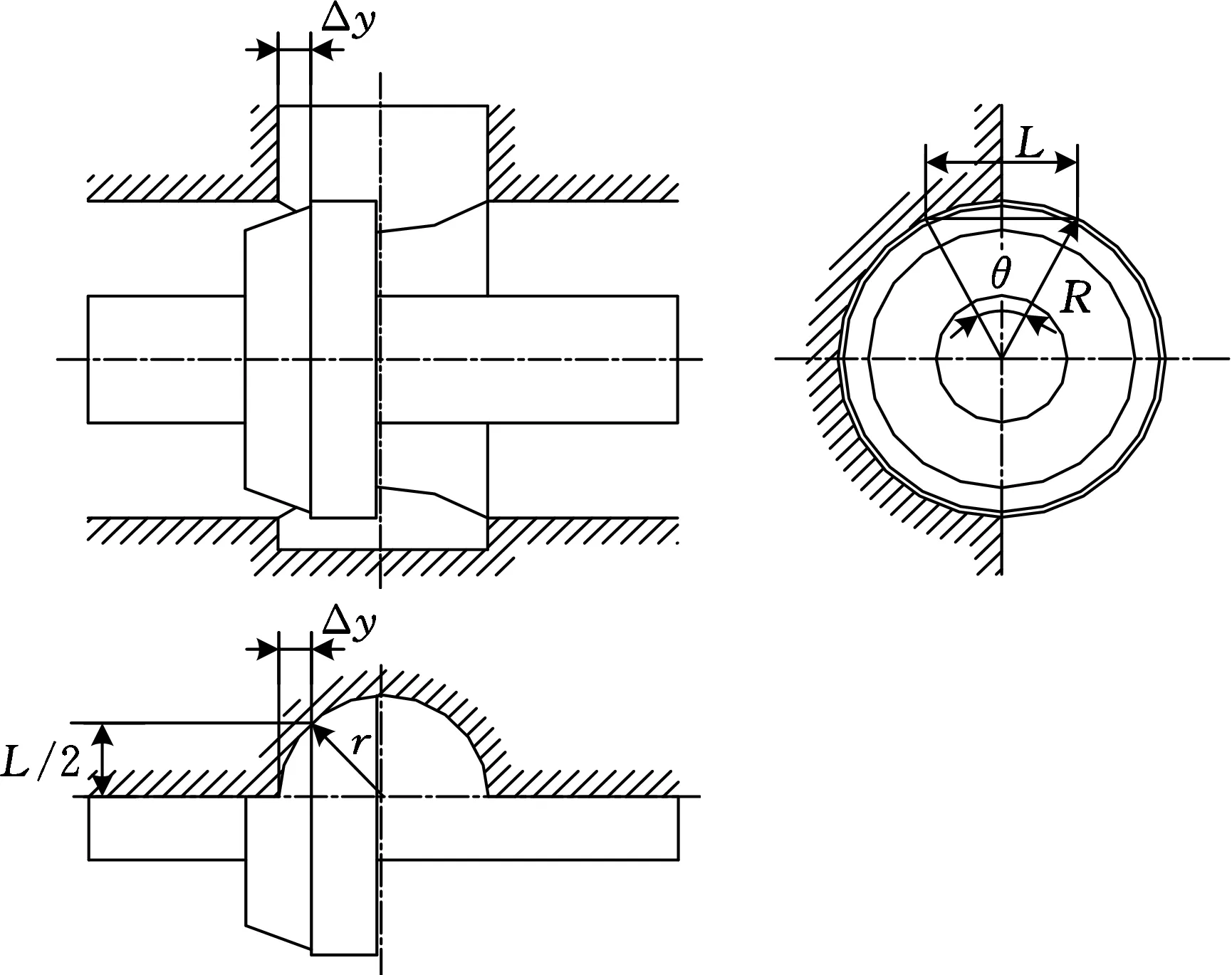
(b)部分锥面结构三视图图6　圆锥面阀芯凸肩滑阀结构结构

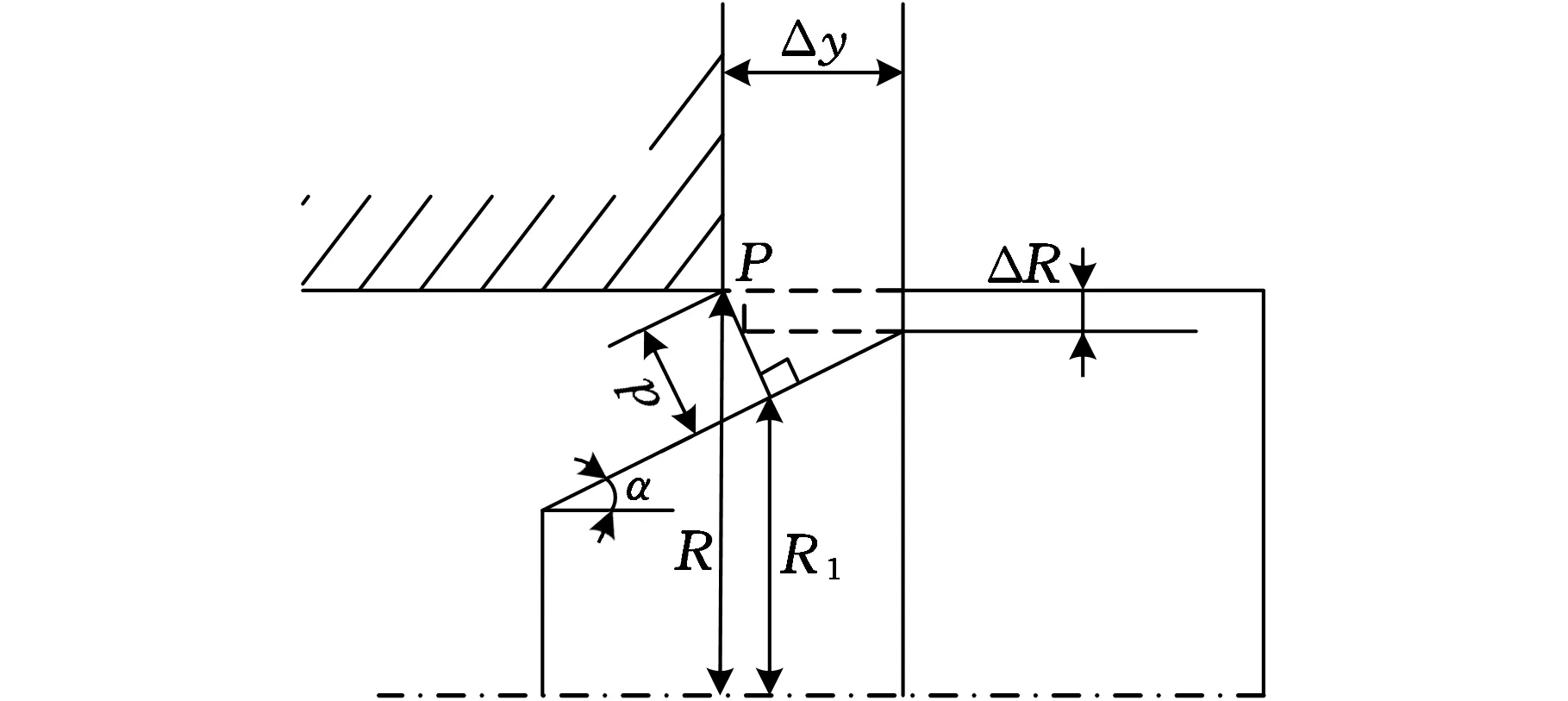
图7　环面计算示意图

将式(9)～式(11)代入式(14),可以将A2表达为关于阀口开度的Δy的函数：

(15)

将式(5)、式(15)代入式(8)，即可得到圆锥面阀口面积A关于阀口开度Δy的函数表达。

2　孔道沉槽流场分析

2.1建立几何模型和网格划分

阀体加工孔道沉槽使得流道结构复杂，图1所示的上下油路的通流能力必然受到影响，尤其是当阀口的流量较大时，下油路的存在与否对整个滑阀的通流能力具有怎样的影响关系尚不明确，本文采用流体仿真的方法对其进行研究[5]。

利用Pro/E建立三维模型，导入到ICEM进行网格划分，仿真中使用到的阀口结构参数及主要边界条件如表1所示。为提高仿真的准确性，采用六面体非结构性网格。圆柱面凸肩滑阀阀口流体域的几何模型如图8所示，阀体有无加工孔道沉槽两种模型的网格划分如图9所示。

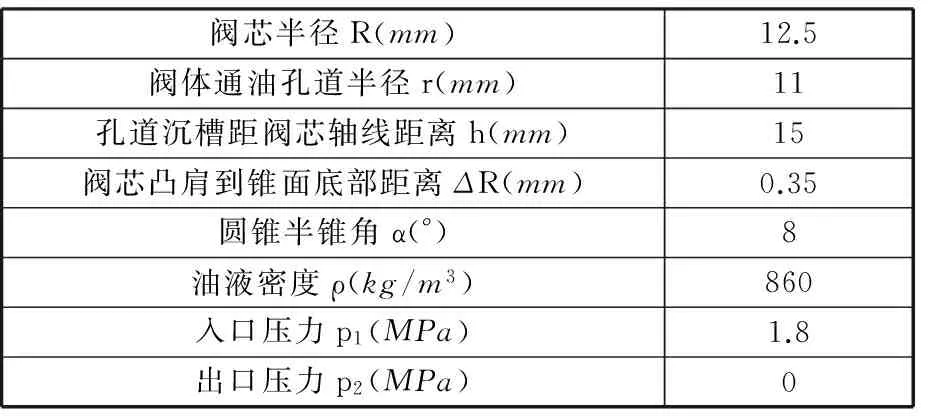
表1　仿真主要参数

图8　圆柱面滑阀流体域的几何模型

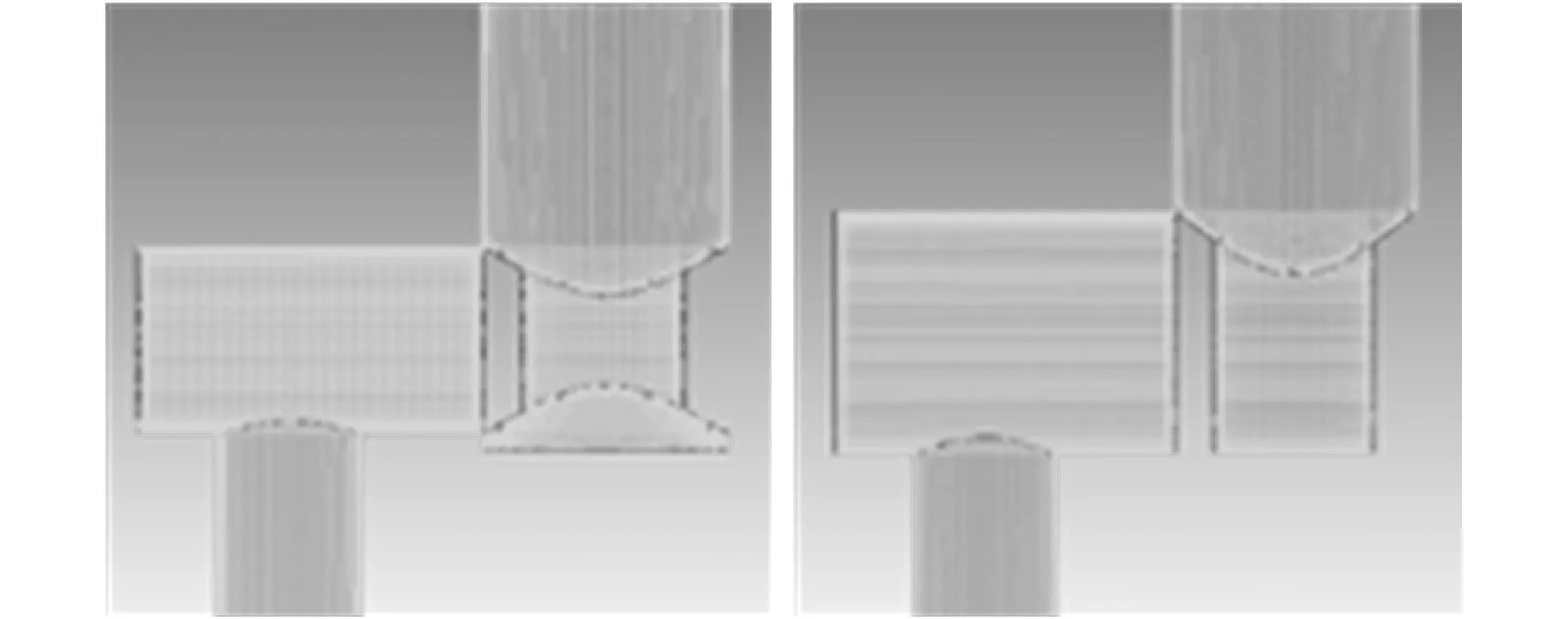
(a)有孔道沉槽　　　　(b)无孔道沉槽图9　两种不同结构网格划分

2.2阀口流场分析

图10以流线图的形式展示了油液流过阀芯节流口时的运动状态，流线是流场中某时刻的一条空间曲线，该时刻位于曲线上流体质点的速度矢量与曲线相切，并且流线分布的疏密程度表征了该区域流速的大小[6]。由流场分析可知：油液流经圆柱面阀芯上下两部分阀口的情形并非完全一致，孔道沉槽区域，液体运动轨迹更长，且受到阀芯凸肩与沉槽底部二次阻碍作用，因此，下节流部分节流作用要强于上节流部分作用，并且这一效应随阀口通过流量的增加而愈加明显。值得一提的是，由图10b可看出，圆锥面阀芯情况下这种情况并不明显，原因在于圆锥面阀芯整体阻碍效果较强、通流量较小。

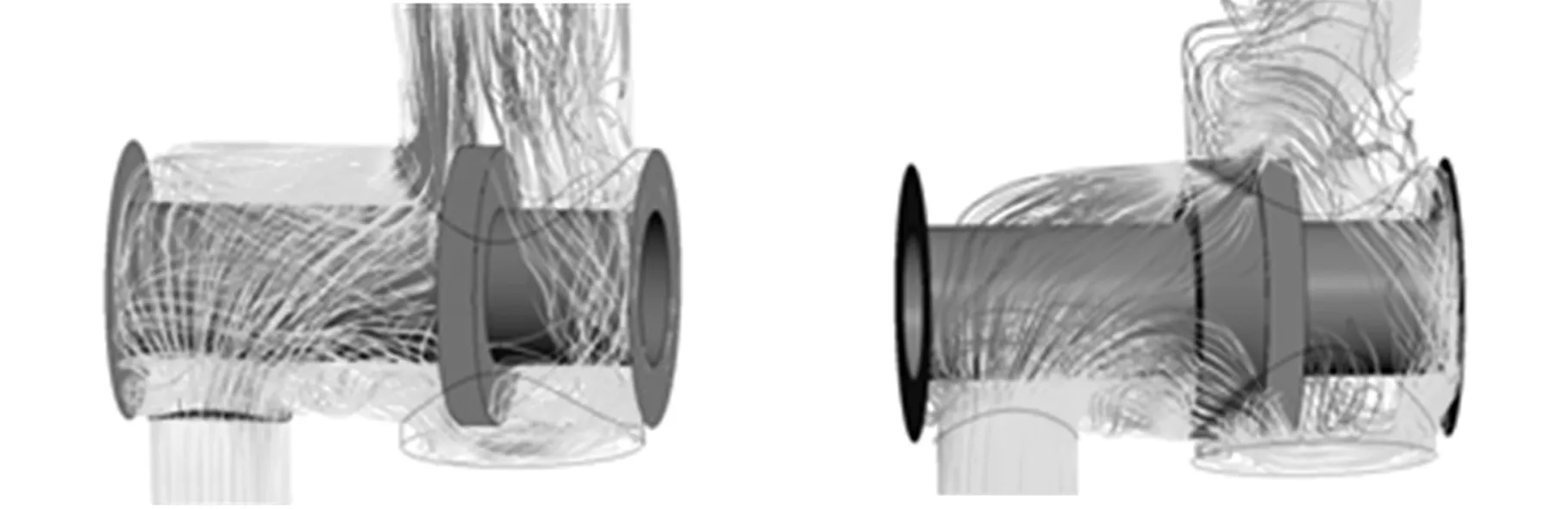
(a)圆柱面阀芯流线分布　(b)圆锥面阀芯流线分布图10　滑阀阀芯节流口流线分布

为了研究圆柱面阀芯阀口孔道沉槽对油液流动的影响，定义阀口流量增益λ为阀体加工孔道沉槽时阀口流量qV1与阀体未加工孔道沉槽时阀口流量QV2的比值，即

λ=QV1/QV2

分别在阀口开度为1mm、2mm、3mm、3.5mm、4mm、4.5mm和5mm处进行流体仿真对比。图11反映了流量增益λ随阀口开度Δy的变化规律，λ随着阀口开度增大呈下降趋势，对其变化关系进行降阶拟合处理[7]，拟合结果为

λ=1.96-0.107Δy

(16)

将仿真比值与拟合比值进行对比，如图11所示。由图11可以看出，随阀口开度增大，流量增益呈减小趋势，即在小流量下孔道沉槽流量增益效果明显，流量增加孔道沉槽阻力随之增加，孔道沉槽流量增益效果逐渐减弱。

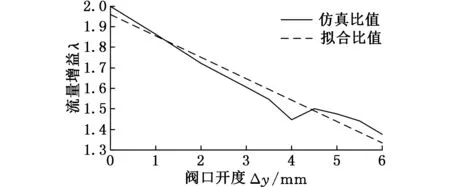
图11　孔道沉槽流量增益λ及其拟合结果

3　实验分析

3.1实验原理与实验设备

为了对理论计算及流场仿真结果进行验证，依托国内某公司的多路阀实验台(图12)，搭建了负载敏感多路阀阀口压力-流量特性实验系统，实验原理图见图13。

图12　多路阀测试实验台

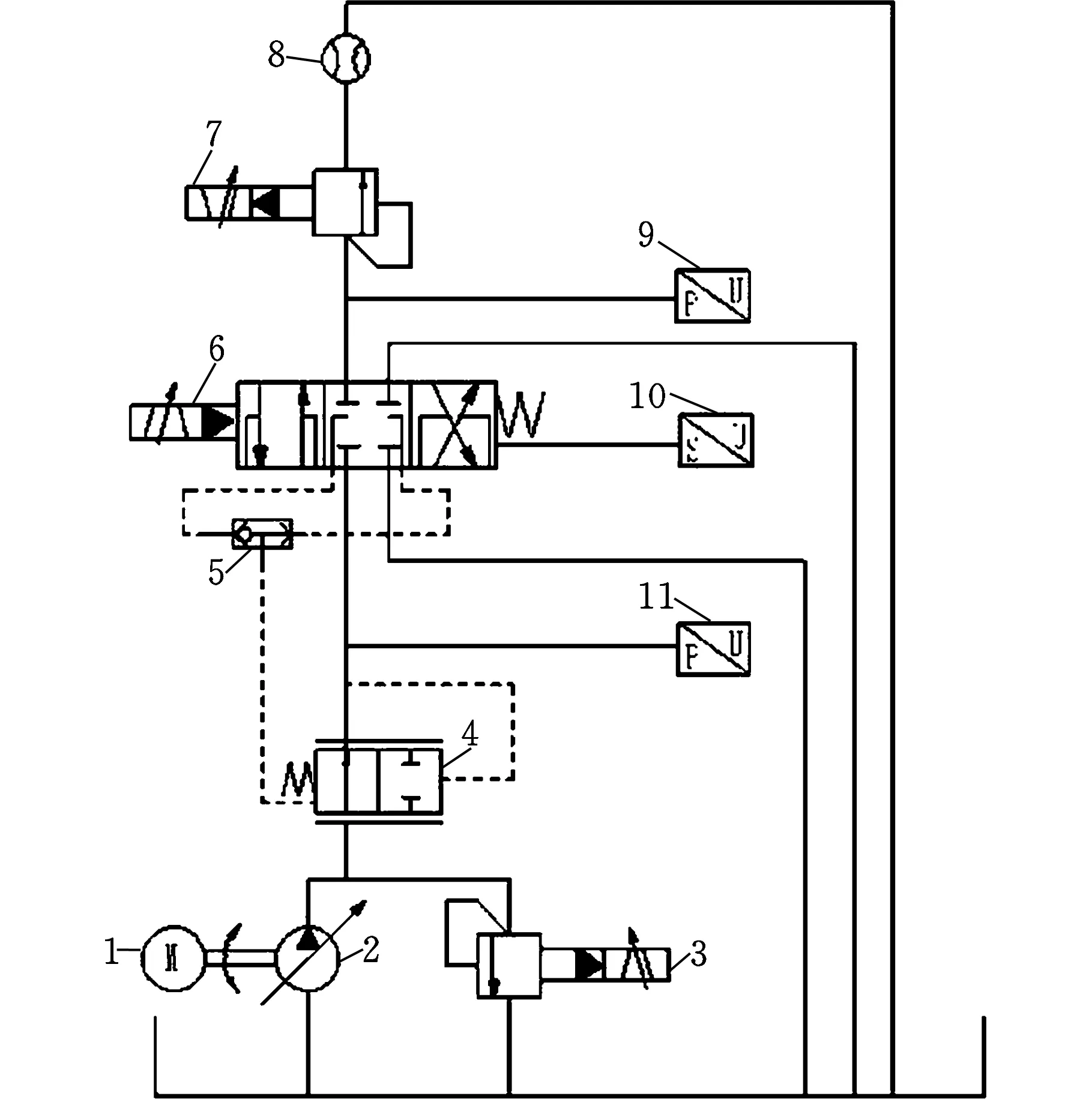
1.电机　2.变量泵　3.电磁溢流阀　4.压力补偿阀　5.梭阀6.主阀　7.电磁溢流阀　8.流量传感器　9.压力传感器10.位移传感器　11.压力传感器图13　阀口流量特性实验原理图

实验研究中所使用的实验阀为AMCA公司生产的多路阀，如图14所示，此阀是一种能控制多个液压执行机构的组合换向阀，一般用于包括工程机械在内的行走机械中。实验中取多路阀A3联，在其阀杆一端连接位移传感器，结合实验台压力传感器和流量传感器，可准确得到圆柱面阀口和圆锥面阀口的压力流量特性曲线。

图14　被测试多路阀

3.2实验结果分析

将随阀口开度变化的流量理论计算值、仿真值与实验数据进行对比。图15为圆柱面阀口修正前后理论计算值、仿真值与实验数据对比图，图16为圆锥面阀口理论计算值、仿真值与实验数据对比图。从图中可以看出，修正后圆柱面阀口三者流量趋势基本吻合，说明对于圆柱面阀口，当设计阀口额定流量较大时，理论计算公式的修正是必要的。而在圆锥面阀口微开时，理论计算、仿真与实验数据存在一定差距，可能是实验台流量传感器在系统较小流量时反应滞后导致的。随着阀口逐渐打开，理论计算值、流体仿真值与实验数据基本一致，从而验证了理论计算公式的准确性。

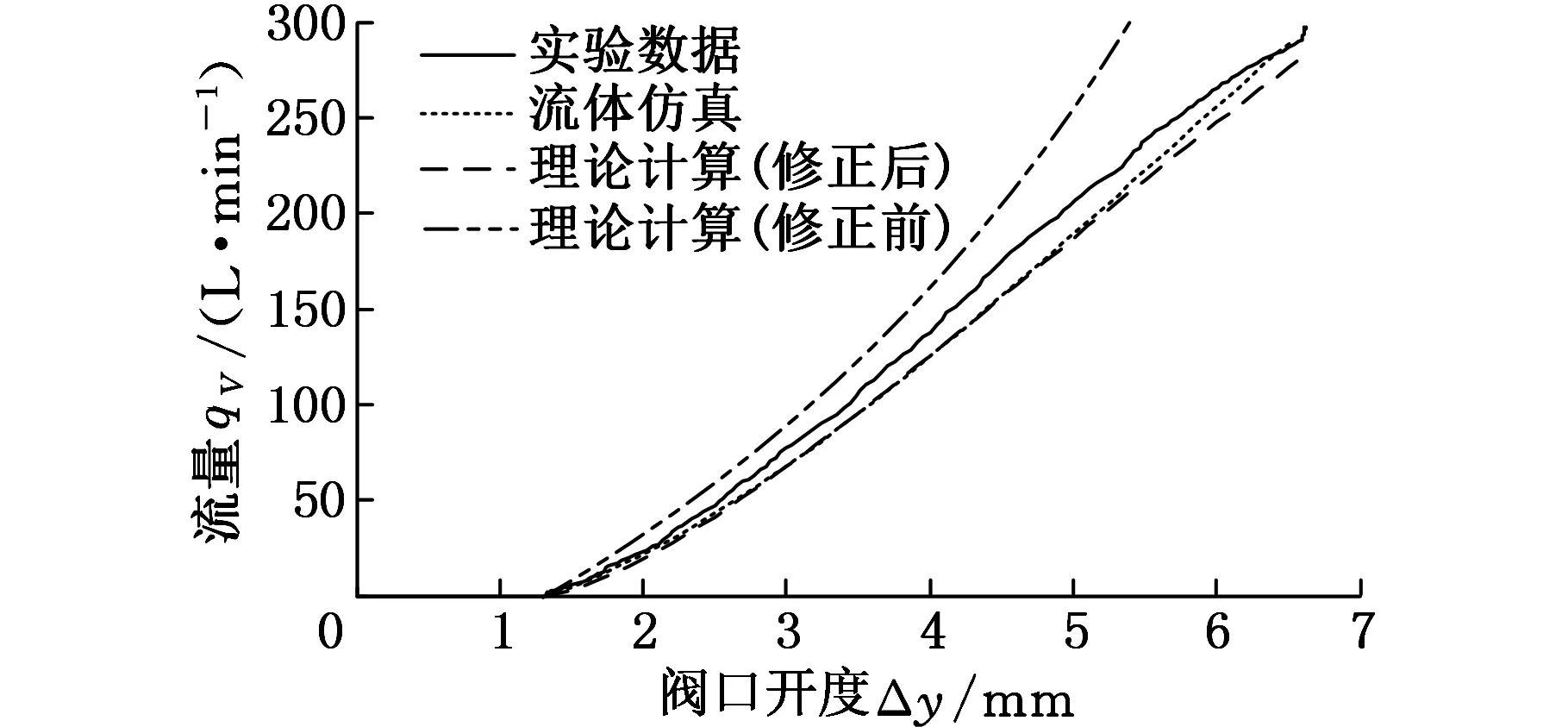
图15　圆柱面阀口通流量随阀口开度曲线

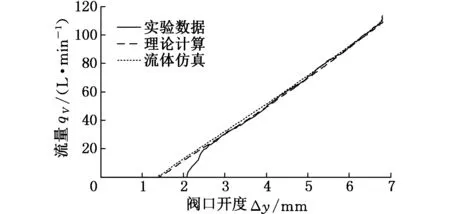
图16　圆锥面阀口通流量随阀口开度曲线

4　结论

本文综合运用滑阀几何结构分析和阀口流场仿真技术，推导了阀体上加工孔道沉槽时的圆柱面阀芯和圆锥面阀芯滑阀阀口面积计算公式，并分别以流场仿真及实验的方法对理论计算结果进行了验证，结果表明：圆锥面阀芯阀口计算结果与实验结果较为接近；而对圆柱面阀芯阀口，在引入孔道沉槽后理论计算与实验结果有较大差距，利用流场分析手段对计算结果进行修正后，得到了与实验结果比较一致的结果。

通过对阀口的流场分析可知：圆形窗口滑阀孔道沉槽设计可以有效提高阀口通流能力，但随通流流量增加，这种增益效果呈减弱趋势，这是在设计孔道沉槽结构时需要考虑的。

阀口过流面积计算公式建立了阀口结构参数与阀口过流面积之间的联系，为圆形窗口下孔道沉槽结构阀口设计及性能预测提供了参考。

[1]杨华勇, 曹剑, 徐兵,等. 多路换向阀的发展历程与研究展望[J]. 机械工程学报, 2005, 41(10):1-5.

Yang Huayong, Cao Jian, Xu Bing, et al. Progress in the Evolution of Directional Control Valves and Future Trends[J]. Chinese Journal of Mechanical Engineering,2005,41(10):1-5.

[2]王春行,徐渌. 液压控制系统[M].北京： 机械工业出版社, 1999.

[3]冀宏,傅新,杨华勇.几种典型液压阀口过流面积分析及计算[J].机床与液压,2003(5):14-16.

Ji Hong, Fu Xin, Yang Huayong. Analysis and Calculation on Typical Shape Orifice Areas in Hydraulic Valves [J]. Machine Tool & Hydraulics,2003(5):14-16.

[4]杜学文,邹俊,傅新,等.节流槽结构对气穴噪声的影响[J].浙江大学学报(工学版), 2007,41(3):456-460，465.

Du Xuewen, Zou Jun, Fu Xin, et al. Effect of Throttling Grooves Structure on Cavitation Noise[J].Journal of Zhejiang University(Engineering Science), 2007,41(3):456-460，465.

[5]Ye Y, Yin C B, Li X D, et al. Effects of Groove Shape of Notch on the Flow Characteristics of Spool Valve[J]. Energy Conversion & Management, 2014, 86(5):1091-1101.

[6]金朝铭. 液压流体力学[M].北京：国防工业出版社, 1994.

[7]Valdés J R, Miana M J, Pütz T. Reduced Order Model for Estimation of Fluid Flow and Flow Forces in Hydraulic Proportional Valves [J]. Energy Conversion & Management, 2008, 49(6):1517-1529.

(编辑袁兴玲)

Analysis of Orifice Area of Slide Valve with Sinking Grooves

Zhang Lijie1,2Wang Lihang1Wang Shuai1Li Dexin1

1.Hebei Key Laboratory of Heavy Machinery Fluid Power Transmission and Control,Yanshan University, Qinhuangdao，Hebei，066004 2.Key Laboratory of Advanced Forging & Stamping Technology and Science,Ministry of Education of China, Qinhuangdao，Hebei， 066004

Multiple valve with its high degree of integration was widely used in the field of engineering machinery, where the valve port form possessed a very important impact on flow control characteristics. Aiming at the cylindrical and conical valve orifice of the spool valve with grooves on the valve body, and based on the structural characteristics and pressure distribution and velocity changes of the internal flow field, and with the equivalent orifice area theory, the calculation equations of orifice area of the cylindrical and conical valve orifice were proposed and analyzed. The results were corrected by the flow field simulation, and the accuracy of the results was verified by experiments. The study results have some reference values for the design and performance prediction of the hydraulic master valve.

multiple valve; sinking groove; orifice area of slide valve; flow field simulation

2015-08-24

国家自然科学基金资助项目(51275438)

TH137

10.3969/j.issn.1004-132X.2016.18.004

张立杰，男，1969年生。燕山大学机械工程学院教授、博士研究生导师。主要研究方向为电液控制系统、机构学及机器人技术。发表论文50余篇。王力航，男，1989年生。燕山大学机械工程学院博士研究生。王帅，女，1988年生。燕山大学机械工程学院硕士研究生。李德新，男，1988年生。燕山大学机械工程学院硕士研究生。