静电放电对羟胺稳定性影响的密度泛函研究

刘建国，张 倩,2，安振涛,2，闫 军,2，王朝阳



静电放电对羟胺稳定性影响的密度泛函研究

刘建国1，张 倩1,2，安振涛1,2，闫 军1,2，王朝阳3

（1.军械工程学院弹药工程系，河北 石家庄，050003；2.军械工程学院 弹药保障与安全性评估军队重点实验室，河北 石家庄，050003；3.华南师范大学化学与环境学院，广东 广州，510006）

为研究静电放电对羟胺稳定性的影响，采用密度泛函B3LYP方法在6-311++G(d,p)基组水平上，计算了羟胺分子在不同外电场（0~0.05a.u.）作用下的基态几何结构、电偶极距、电荷分布及分子总能量，并分析了HOMO能级、LUMO能级、能隙随外电场变化规律，然后利用杂化CIS-DFT方法在相同基组下研究了外电场对羟胺分子前9个激发态的影响。结果显示：分子的几何结构、电荷分布与外电场的大小呈现强烈的依赖关系。随着外电场的不断增加，分子的总能量逐渐减小，偶极距逐渐增大，能隙逐渐减小。同时，外电场对羟胺分子的激发态的激发能、波长和振子强度都有一定的影响。

羟胺；静电放电；稳定性；密度泛函

羟胺（Hydroxylamine，HA）是氮的衍生物，是生产新型高能氧化剂如硝酸羟胺等的主要原材料。然而，羟胺的不稳定性给其应用和存储带来了很大困难。为此，相关学者对羟胺稳定性影响因素进行了深入的研究。Wang Qingsheng等[1]利用量子化学计算方法，结合密度泛函理论对羟胺在热作用下的分解路径进行了研究，Wei Chunyang等[2]通过量子化学计算和实验对羟胺在酸性溶液中的分解机理进行了研究。但从目前的文献来看，对静电放电作用下羟胺稳定性的研究还未见报道，而分子在外电场作用下往往会发生一系列的化学变化和现象，比如新自由基的生成、化学键的断裂和新激发态的出现等[3-5]。因此，采用量子化学的计算方法研究外电场对羟胺分子结构和激发态的影响，为静电放电对羟胺稳定性的影响提供理论上的参考具有重要意义。

1 理论和计算方法

外电场作用下分子体系的哈密顿量为[6]:

（1）

式（1）中：0为无外电场时的哈密顿量；int为外电场与分子体系的相互作用的哈密顿量。当在偶极近似下，外电场与分子体系的相互作用哈密顿量可以表示为：int=-·（2）

式（2）中：为分子电偶极距。

根据Grozema[7]等提出的模型，在电场作用下的激发能exc与电场强度、电偶极距和极化率的变量和满足关系：

式（3）中：exc(0)为无电场下的激发能，振子强度1u[8]为：

图1 无外电场作用下羟胺分子的结构

2 计算结果与讨论

2.1 外电场对分子基态结构及电荷布局分布的影响

采用密度泛函B3LYP/6-311++G(d,p)方法，在Z轴（N-O连线）方向加载不同强度的外电场（0~0.05a.u.），对羟胺分子的基态构型进行优化。在外电场作用下，分子的稳定构型是由分子内应力和外场力共同决定，强外电场产生的外场力大于分子的内应力，电子将逆着电场方向发生转移[8]，结果表现为键长、键角、偶极距和电荷布局分布等的变化。其中，外电场作用下羟胺分子基态优化的几何参数如表1所示。

表1 不同外电场下羟胺分子的基态键长R、键角A

从表1可以看出，分子几何参数与外电场的强度之间存在着明显的依赖关系。随着外电场的逐渐增加，羟胺分子键长(1,2)先减小后增大，键长(1,3)、(3,5)、(3,4)逐渐增大，且呈线性递增的变化规律。具体表现在，键长(1,2)随着外电场的增强先由0.962 8Å减小到0.960 2Å，然后由0.960 2Å增加到0.965 0Å。键长(3,4)和(3,5)分别从1.018 7Å增加到了1.027 7Å，键长(1,3)从1.443 3Å增加到了1.465 0Å，键长(1,3)的增加速度更快一点，说明键长(1,3)受外电场的影响更大一点。从表1中可以看出，随着外电场的逐渐增加，羟胺分子键角(2,1,3)逐渐增大，(1,3,4)、(1,3,5)、(4,3,5)逐渐减小，且变化规律呈线性递减的趋势。具体表现在：键角(2,1,3)随外电场的增加从102.81º增大到了106.36º，键角(1,3,4)和(1,3,5)分别从104.26º减小到了102.55º，键角(4,3,5)从106.12º减小到了100.54º，键角(4,3,5)的减小速度更快一点，说明键角(4,3,5)受外电场的影响更大一些。

从表2的电荷布局分布可以看出，羟胺分子的电荷在电场的作用下发生电子转移，从而引起电荷分布的变化，但各原子受电场影响的情况不同。在羟胺分子中，O原子和N原子带负电荷，呈负电性，H原子带正电荷，呈正电性。由于羟胺分子本身不带电荷，所以O原子、N原子和3个H原子所带的电荷总和为零。随着外电场的不断增强，O原子的电荷分布系数绝对值逐渐减小，N原子电荷分布系数绝对值逐渐增大。例如，=0a.u.时，O原子电荷分布系数为-0.2807，N原子电荷分布系数为-0.496 5；=0.05a.u.时，O原子电荷分布系数为-0.087 3，N原子电荷分布系数为-0.720 4，说明O原子负电性随外电场的增大逐渐降低，N原子负电性随外电场的增大逐渐增强。电场对H原子周围电荷密度影响也比较大，随着外电场的不断增强，H2原子电荷分布系数逐渐较小，H4和H5原子电荷分布系数逐渐增大。例如，=0a.u.时，H2原子电荷分布系数为0.2777，H4和H5原子正电荷密度为0.249 8，=0.05a.u.时，H2原子电荷分布系数为0.086 2，H4和H5原子电荷分布系数为0.360 8，说明H2原子正电性随外电场的增大逐渐降低，H4和H5原子正电性随外电场的增大逐渐增强。

表2 不同外电场下羟胺分子的电荷布局分布

2.2 外电场对分子总能量和偶极距的影响

分子总能量随外电场强度的变化情况如表3和图2所示。

表3 基态总能量、偶极距随外电场的变化

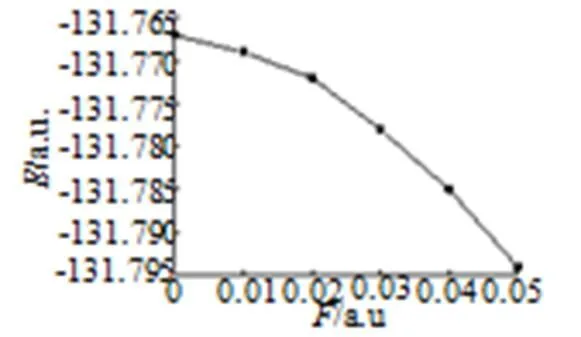
图2 分子总能量随外电场强度变化的关系

从图2中可以看出，随着外电场的逐渐增加，体系的总能量逐渐减小。当=0a.u.时，分子体系总能的值最大为-131.767a.u.，随后当外电场增加时，体系的总能量不断减小，当=0.05a.u.时，分子体系的总能量减小到-131.794a.u.。分子偶极距随外电场强度的变化情况如表3和图3所示。

图3 偶极距μ随外电场强度变化的关系

从图3中可见，分子偶极距随着外电场的增加逐渐增大，外电场对分子偶极距的影响近似呈线性递增的关系。例如，当=0a.u.时，分子偶极距为0.676 3Debye，当=0.05a.u.时，分子偶极距为2.748 4 Debye，后者比前者增加了3.06倍。偶极距越大表明分子的极性越强[11]，说明外电场增强了羟胺分子的极性。

2.3 外电场对分子能级分布的影响

采用密度泛函B3LYP/6-311++G(d,p)的方法对羟胺分子在不同外电场作用下的稳定基态构型下进行优化计算，得到了不同外电场作用下的羟胺分子轨道能量，既羟胺分子体系的最高占据轨道（HOMO）能量E，最低空轨道（LUMO）能量E和能隙E，其中能隙的计算公式为，见表4。

表4 不同外电场下羟胺分子最高占据轨道能量、最低空轨道能量和能隙

最高占据轨道（HOMO）能级反映了失去电子能力的强弱，HOMO能级越高，分子越容易失去电子。最低空轨道LUMO能级在数值上与分子的电子亲和势相当，LUMO能级越低，分子越容易得到电子[12-13]。HOMO与LUMO能量的差值为能隙E，E反映了电子从占据轨道向空轨道发生跃迁的难易程度，在一定程度上代表了分子参与化学反应的能力。

图4为E、E随外电场强度的变化。从表4和图4可以看出，随着外电场强度的不断增强，E逐渐增大，E逐渐减小，从而导致最高占据轨道与最低空轨道之间的能隙逐渐减小。另外，从图4可以看出外电场对分子最低空轨道的影响比较大，最低空轨道的能级比最高占据轨道的能级变化得快，从而导致能隙随外电场的变化几乎呈线性递减的规律，其变化情况如图5所示，说明在外电场作用下分子参与化学反应的能力得到增强。

图4 HOMO和LUMO轨道能量随外电场强度变化的关系

图5 能隙随外电场强度变化的关系

2.4 外电场对激发态的激发能、波长和振子强度的影响

在不同外电场下对基态稳定构型优化的基础上，采用CIS/6-311++G(d,p)方法计算了羟胺分子在不同外电场作用下前9个激发态的激发能、波长及振子强度，计算结果列于表5~7中。

表5 不同外电场下羟胺分子的前9个激发态的激发能

从表5可以看出，在引入外电场的情况下，激发态的激发能随外电场的变化比较复杂。随着外电场的不断增加，第1、2、5、6、9激发态的激发能不断增大，第3、4、7、8激发态的激发能逐渐减小。分析表6可以看出，随着外电场的增加，第1、2、5、6、9激发态的波长逐渐减小，第3、4、7、8激发态的波长不断增大，且激发态的跃迁光谱都集中在紫外区。激发能的变化趋势与激发态波长的变化趋势正好相反，这是由于电场的增大导致激发能的改变，从而引起激发态波长的变化。由振子强度（表7）的计算可知，外电场对激发态的振子强度的影响也比较复杂。随着外电场的不断增大，第2、3、5、6、7、8、9激发态的振子强度整体上逐渐增大，第1、4激发态的振子强度整体上逐渐减小。=0a.u.时，第8激发态的振子强度为0，属于禁阻跃迁，其他激发态的振子强度均不为0，可以发生电子跃迁。同时，也说明了电子跃迁光谱的强度受外电场的影响。

3 结论

为研究静电放电对羟胺稳定性的影响，本文采用B3LYP/6-311++G(d,p)方法优化得到了不同外电场作用下羟胺分子的基态稳定构型，讨论了分子的几何构型、电偶极距、电荷分布和总能量等随外电场的变化。结果显示，分子的几何结构、电荷分布与外电场的大小呈现强烈的依赖关系，随着外电场的增加，分子的总能量不断减小，偶极距不断增大，能隙不断减小，表明分子的极性增加，参与化学反应的能力得到增强。然后利用杂化CIS-DFT方法，在相同基组下研究了外电场对羟胺分子前9个激发态的激发能、波长和振子强度的影响。结果表明，随着外电场的不断增加，第1、2、5、6、9激发态的激发能不断增大，激发态波长逐渐减小，第3、4、7、8激发态的激发能逐渐减小，激发态波长不断增大，且电子跃迁光谱都集中在紫外区。另外，外电场对振子强度的影响也很复杂，有的增大有的减小，同时也说明电子跃迁光谱强度受外电场的影响。综上所述，在外电场作用下，羟胺分子的极性增强，参与化学反应的能力提高，且其激发态也受到了外电场的影响，为研究静电放电对羟胺稳定性的影响提供了重要的理论参考。

[1] Wang Qingsheng, Wei Chunyang, Perez Lisa M, etal. Thermal decomposition pathways of hydroxylamine: Theoretical investigation on the initial steps[J]. J Phys Chem(A), 2010, 114(34): 9 262-9 269.

[2] Wei Chunyang, Saraf Sanieev R, Rogers Willian J, etal. Thermal runaway reaction hazards and mechanisms of hydroxylamine with acid/base contaminants[J]. Thermochi- mica Acta, 2004(421): 1-9.

[3] Yan Zhang, Yuanfeng Ye, Yanwei Li, etal. Ab initio investigations of quaterthiophene molecular wire under the interaction of external electric field[J]. Journal of Molecular Structure: Theochem, 2007, 802(1-3): 53-58.

[4] Yoshishige Okuno, Mie Minagawa, Hidetoshi Matsumoto, etal. Simulation study on the influence of an electric field on water evaporation[J]. Journal of Molecular Structure: Theochem, 2009, 904(1-3): 83-90.

[5] Haddou El Ghazi, Anouar Jorio. Excited-states of hydrogenic-like impurities in InGaN-GaN spherical QD: Electric field effect[J]. Physica B, 2013(430): 81-83.

[6] 蔡绍洪,周业宏,何建勇.外场下丙烯酸甲酯的激发特性研究[J].物理学报, 2011, 60(9):1-7.

[7] 周业宏,蔡绍洪.氯乙烯在外电场下的激发态结构研究[J]. 物理学报, 2010, 59(11): 7 749-7 755.

[8] Yanwei Li, Jianwei Zhao, Geping Yin. Theoretical investigations of oligo(phenylene ethylene)molecular wire: Effects from substituents and external electric field[J]. Computational Materials Science, 2007, 39(4): 775-781.

[9] 石国升, 丁益宏. 双取代铵氧化物(R2HNO)与双取代羟胺(R2NOH)的相互转换机制的量子化学研究[J]. 化学学报, 2008, 66(22): 2 483-2 488.

[10] Jalbout A F, Nazari F, Turker L. Gaussian-based computations in molecular science[J]. Journal of Molecular Structure: Theochem, 2004, 671(1): 1-21.

[11] Neetu Pandey, Richa Gahlaut, Priyanka Arora. Study of dipole moments of some coumarin derivatives[J]. Journal of Molecular Structure, 2014(1 061): 175-180.

[12] Tôru Sakai, Munehisa Matsumoto, Kouichi Okunishi, etal. Energy gap of spin nanotube[J]. Physica E: Low-Dimensional Systems and Nanostructures, 2005, 29(3-4): 633-636.

[13] L P Horwitz, E Z Engelberg. Energy gaps in a spacetime crystal[J]. Physics Letters, 2009, 374(1): 40-43.

DFT Study on the Influnce of Electrostatic Discharge on the Stability of Hydroxylamine

LIU Jian-guo1, ZHANG Qian1,2, AN Zhen-tao1,2, YAN Jun1,2, WANG Chao-yang3

（1.Department of Ammunition Engineering, Ordnance Engineering College, Shijiazhuang，050003；2.Military Key Laboratory for Ammunition Support and Safety Evaluation, Ordnance Engineering College, Shijiazhuang，050003；3.School of Chemistry and Environment, South China Normal University，Guangzhou，510006）

To study the influence of electrostatic discharge on the stability of hydroxylamine, the ground state parameters, dipole moment, charge distribution energy levels and HOMO-LOMO gap of hydroxylamine under different electric fields ranging from 0.00~0.05a.u. were optimized, by use of density functional theory (DFT)/B3LYP at 6-311++G(d,p) basis set level. The excitation energies, the wavelengths, the oscillator strengths from ground state to the first nine different excited states were calculated employing the revised hybrid CIS-DFT method. The results show that the molecular geometry and charge distribution is strongly dependent on electric field strength. The whole energy is proved decreasing, the dipole moment is increased, and the energy gap is decreased. Meanwhile, the external electric field had an effect on the excitation energies, the wavelengths, and the oscillator strengths.

Hydroxylamine；Electrostatic discharge；Stability；DFT

1003-1480（2016）02-0044-05

TQ560.1

A

2015-09-06

刘建国（1988 -），男，博士研究生，主要从事火工品的合成与分子模拟等研究。

“十二五”装备预研项目（40404010303）。