误差传递理论在解决实际问题中的应用

2016-10-12韩唯伟倪敏曹政徐小林

考试周刊 2016年75期

韩唯伟++倪敏++曹政++徐小林

一、引言

高考是反映一个学生的学习水平的最直接的方式。物理是一门以实验为基础的学科，因此要想反映学生的物理学习水平，就要通过实验题考查学生的物理知识水平。随着教育观念的不断更新，人们逐渐意识到培养学生解决实际问题的能力比传授知识本身更重要。因此，物理实验的考查更趋向于解决实际问题的能力的考查[1]。

下面笔者就以2015年上海市高考物理第27题为例，通过传统解法和运用误差传递理论的解法对比突出误差传递理论在解题中的优势。

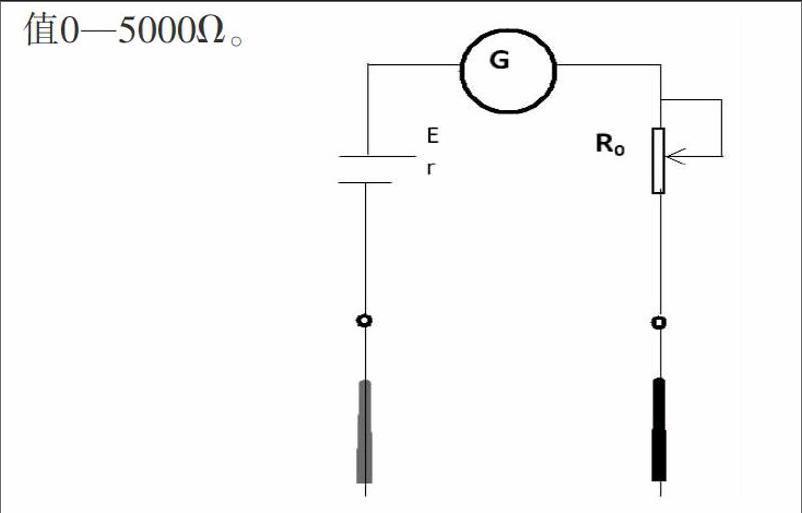
如图是一个多用表欧姆挡内部电路示意图。电流表满偏电流0.5mA、内阻10Ω；电池电动势1.5V、内阻1Ω；变阻器R阻值0—5000Ω。

（1）该欧姆表的刻度值是按电池电动势为1.5V刻度的，当电池的电动势下降到1.45V、内阻增大到4Ω是仍可调零。调零后R阻值将变？摇？摇？摇（选填“大”或“小”）；若测得某电阻阻值为300Ω，则这个电阻的真实值是？摇？摇？摇Ω

（2）若该欧姆表换了一个电动势为1.5V，内阻为10Ω的电池，调零后测量某电阻的阻值，其测量结果？摇？摇？摇（选填“偏大”、“偏小”或“准确”）。

二、传统解题方法

1.试题解析

在解答第一个问题的时候我们知道，只要多用电表满偏，则流过表头的电流就是恒定的。因此只需要计算在相同满偏电流的前提下，变换阻器阻值R的大小，进而比较得出变大变小；在计算300Ω的电阻的真实值时，假设电动势仍为1.5v，则可以计算出此时流过表头的电流。实际情况是，电源电动势下降了，但是流过表头的电流没有变。因此，只需计算电动势为1.5v，电流相同的情况下的待测电阻的阻值就可以了；对于第二小题，更换电池后进行了调零，因此对于测量结果是没有影响的仍然准确。

2.解题过程及答案

（1）当电动势为1.5v时，则，对电表进行调零后，电流表满偏，则：

（2）电源电动势和内阻的变化在调零后，改变的只是调零电阻的阻值，对测量待测电阻的阻值是没有影响的。因此，测量结果准确。

三、运用误差传递理论解决问题

1.误差传递公式

四、结语

本文利用误差传递的理论解决了多用电表的电池电动势和内阻发生变化后给测量结果带来偏差的问题。相比传统的方式利用误差传递理论解决该问题有以下优点：

（1）简化计算：利用误差传递理论，可以避免调零电阻的计算，只需要根据电池电动势的变化，就可以计算出实际的待测电阻的阻值，相比于传统方法简便了许多；

（2）提高正确率：利用误差传利理论在计算过程中，由于降低了复杂的计算，同时也降低了计算错误的几率，因此有效提高了计算的正确率；

（3）拓宽思路：利用误差传递理论解决该问题，是一种新的思路。学生在解题过程中尝试新的思路，可以锻炼思维能力，培养创造力。

本文通过一道高考题探讨了误差传递理论在解题中的应用。误差传递理论在解题中的应用还有很多方面，在此只是抛砖引玉，以期引起广大教育工作者更深、更全面的思考[5]。

参考文献：