Hardy Type Estimates for Riesz Transforms Associated with Schr¨odinger Operators on the Heisenberg Group

Yu Liu and Guobin Tang

School of Mathematics and Physics,University of Science and Technology Beijing, Beijing 100083,China



Hardy Type Estimates for Riesz Transforms Associated with Schr¨odinger Operators on the Heisenberg Group

Yu Liu and Guobin Tang∗

School of Mathematics and Physics,University of Science and Technology Beijing, Beijing 100083,China

Analysis in Theory and Applications

Anal.Theory Appl.,Vol.32,No.1(2016),pp.78-89

Heisenberg group,stratified Lie group,reverse H¨older class,Riesz transform, Schr¨odinger operator.

AMS Subject Classifications:52B10,65D18,68U05,68U07

1　Introduction

Let L=−∆Hn+V be a Schr¨odinger operator,where∆Hnis the sub-Laplacian on the Heisenberg group Hnand V the nonnegative potential belonging to the reverse H¨older class Bq1for some q1≥Q/2 and Q＞5.In this paper we consider the Riesz transforms associated with the Schr¨odinger operator L

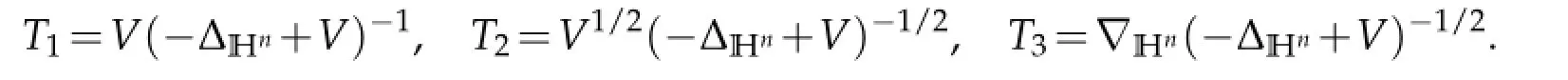
Weare interestedintheHardytypeestimatesfortheRiesztransform Ti,i=1,2,3.Inrecent years,some problems related to Schr¨odinger operators and Schr¨odinger type operators on the Heisenberggroup and othernilpotent Lie group have beeninvestigated by a numberof scholars(see[2,3,5–10,12]).Among thesepapersthecore problemis the researchof estimates for Riesz transforms associated with the Schr¨odinger operator L.As we know, C.C.Lin,H.P.Liu and Y.Liu have proved that the operatorisbounded fromin[5].In this paper we will show that the other two operators T1and T2are also bounded fromAt the last section,we simply state the results on the stratified Lie group.

In what follows we recall some basic facts for the Heisenberg group Hn(cf.[11]).The Heisenberg group Hnis a lie group with the underlying manifold Rn×Rn×R,and the multiplication

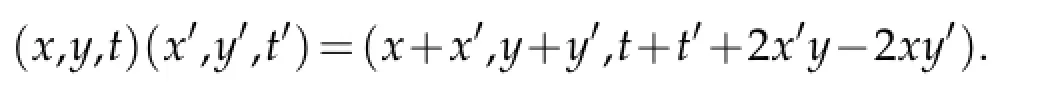
A basis for the Lie algebra of left-invariant vector fields on Hnis given by

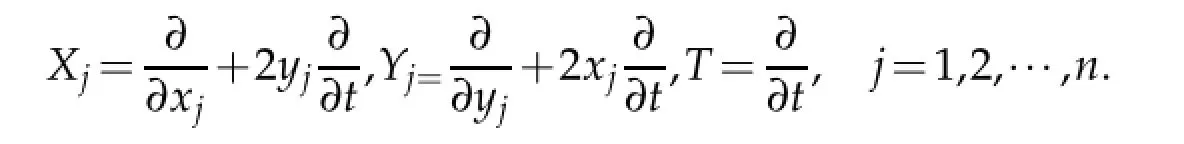
All non-trivial commutation relations are given by[Xj,Yj]=−4T,j=1,2,···,n.Then the sub-Laplacian∆Hnis defined byand the gradient operatoris defined by

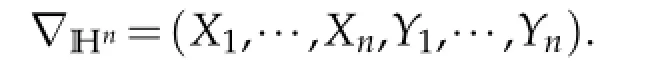
The dilations on Hnhave the form δλ(x,y,t)=(λx,λy,λ2t),λ＞0.The Haar measure on Hncoincides with the Lebesgue measure on Rn×Rn×R.We denote the measure of any measurable set E by|E|.Then|δλE|=λQ|E|,where Q=2n+2 is called the homogeneous dimension of Hn.

We define a homogeneous norm function on Hnby

This norm satisfies the triangular inequality and leads to a left-invariant distant function d(g,h)=|g−1h|.Then the ball of radius r centered at g is given by

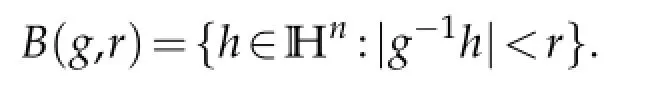
The ball B(g,r)is the left translation by g of B(0,r)and we havewhere α1=|B(0,1)|,but it is not important for us.

Anonnegativelocally LqintegrablefunctionV onHnissaid tobelongto Bq(1＜q＜∞) if there exists C＞0 such that the reverse H¨older inequality

holds for every ball B in Hn.

Definition 1.1.For g∈Hn,the function m(g,V)is defined by

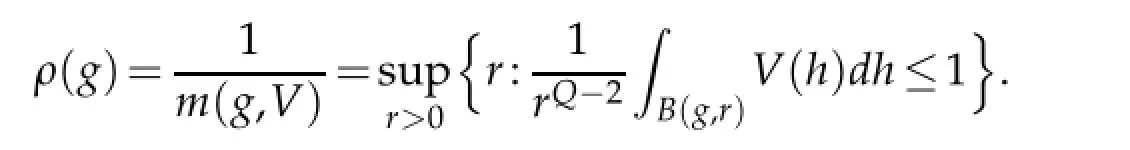
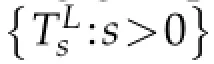
Definition 1.3.Let 1＜q≤∞.A function a∈Lq(Hn)is called an-atom if r≤ρ(g0)and the following conditions hold:

(i)suppa⊂B(g0,r),r＞0,

It follows from(i)and(ii)in Definition 1.3 that aatom is also aatom for 1≤q＜∞.We have the following atomic characterization by the results in[5]and[12].

Proposition 1.1.Let 1＜q≤∞and f∈L1(Hn).Thenif and only if f can be written aswhere ajare-atoms,

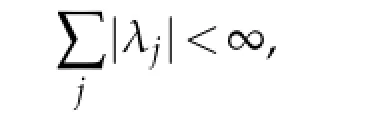
and the sum converges in thequasi-norm.Moreover,

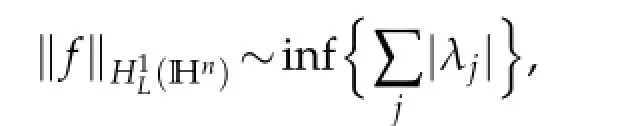
where the infimum is taken over all atomic decompositions of f into-atoms.

Now we are in a position to give the main results.

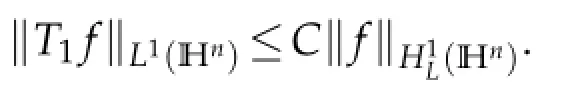
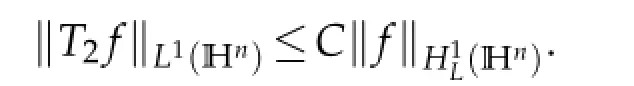
Remark 1.1.It is natural to ask whether the operators T1and T2are bounded fromintoeven fromintowith suitable p＜1?We think these problems are true.But their proofs depend on the molecular characterization ofWe will investigate the topic in our another paper.

2　The auxiliary function m(g,V)

In this section,we will recall some related lemmas about the auxiliary function.Refer to[3]for the proofs.We assume that the potential V(g)is nonnegative and belongs to Bq1for q1≥Q/2.

Lemma 2.1.There exists a constant C＞0 such that,for 0＜r＜R＜∞,

Lemma 2.2.

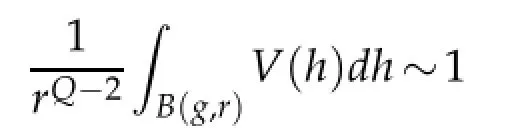
holds if and only if r∼ρ(g).

Lemma 2.3.There exist C＞0 and l0＞0 such that

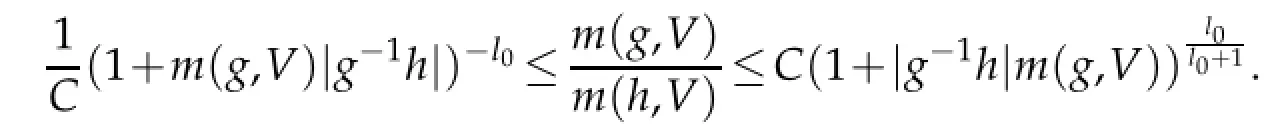
In particular,ρ(g)∼ρ(h)if|g−1h|＜Cρ(g).

Lemma 2.4.There exist C＞0 and l1＞0 such that

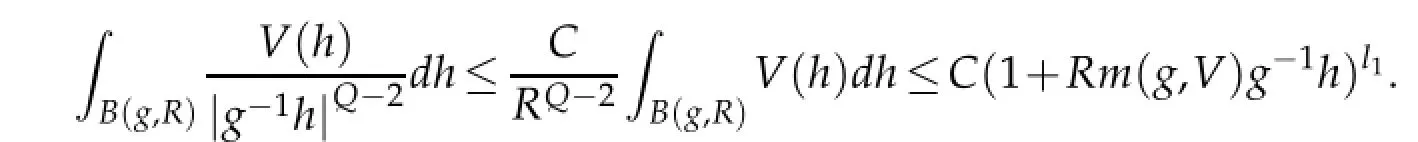
3　Estimates of fundamental solution for the Schr¨odinger operator

In this section we recall some estimates of fundamental solution of the operatorV+λ and estimates of the kernels of Riesz transforms.Let Γ(g,h,λ)be the fundamental solution of the operatorwhere λ∈[0,∞).Obviously,Γ(g,h,λ)=γ(h,g,λ).

The proofs of the following Lemmas have been given in[3].

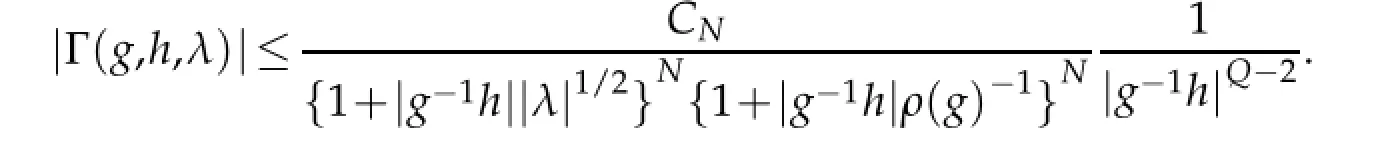
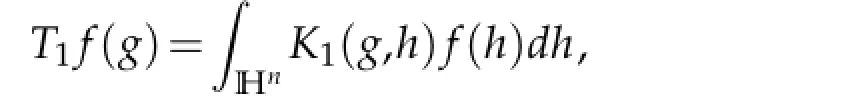
where K1(g,h)=V(g)Γ(g,h)and Γ(g,h)=Γ(g,h,0).By functional calculus,the operator

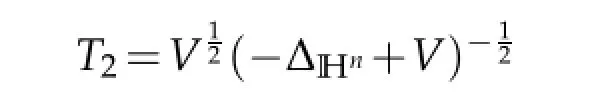
is defined by

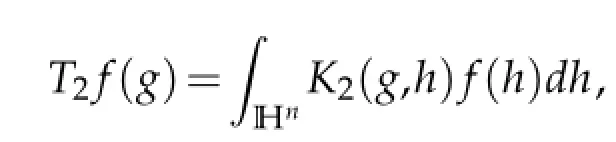
where

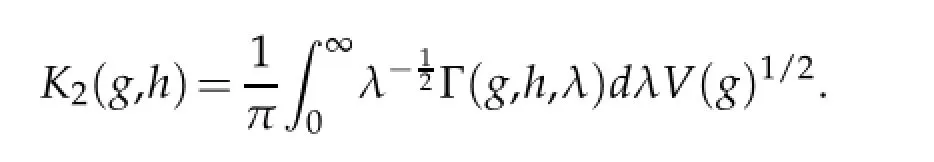
The proofs of the following lemmas can be found from Lemma 3 and Lemma 4 in[4].

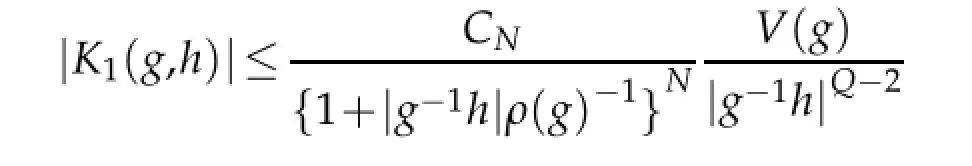
and

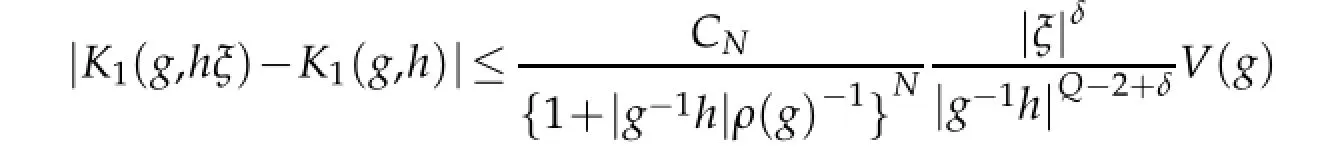
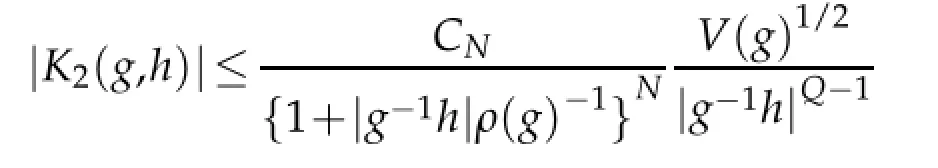
and

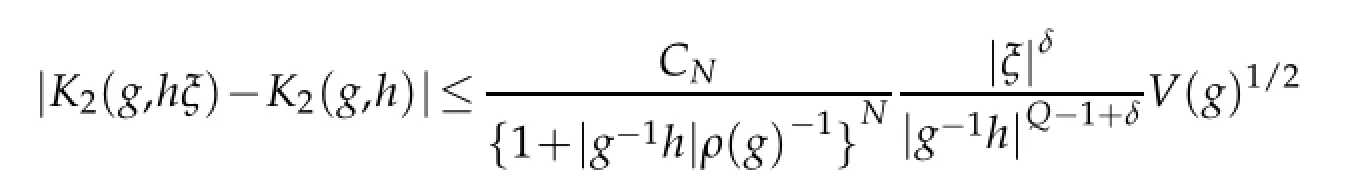
4　Proofs of main results

The aim of this section is to prove the Hardy type estimates for Riesz transforms T1and T2on the Heisenberg group Hn.

The following propositions prove the Lp(Hn)boundedness of Riesz transforms associated with the Schr¨odinger operatorThe proofs have been given in[3].

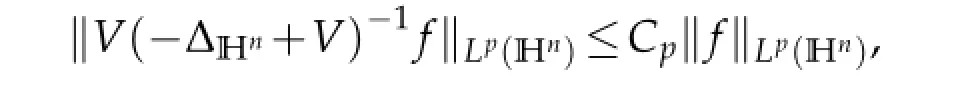
where the constant Cp＞0 doesn’t depend on f.

Proposition 4.2.Suppose V∈Bq1,Q/2≤q1＜Q,then for 1＜p≤2q1,

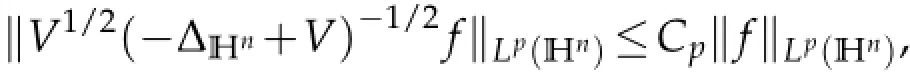
where the constant Cp＞0 doesn’t depend on f.

We can arrive at the proof of Theorem 5.1 by the following Lemma.

Lemma 4.1.Let q1＞Q/2.There exists q with 1＜q＜q1such that

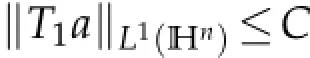
Proof.Assumethatsuppa⊆B(g0,r).Wedividedintotwocasesfortheproofofthelemma:

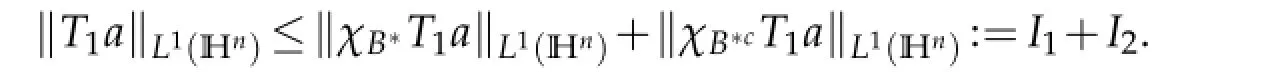
According to Proposition 4.1,T1is bounded from Lq(Hn)into Lq(Hn),thus via the H¨older inequality we get

For I2,using the Minkowski inequality,Lemma 2.3 and Lemma 2.4,noting thatwe have

where we choose N sufficiently large and use the assumption

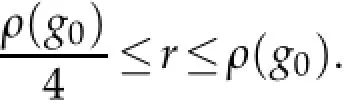
then

Obviously,similar to the proof of Case 1,it is easy to get

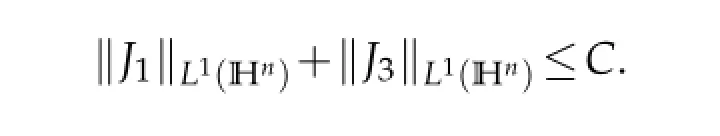
For J2.Using Lemma 3.2 and Lemma 2.3,we can get

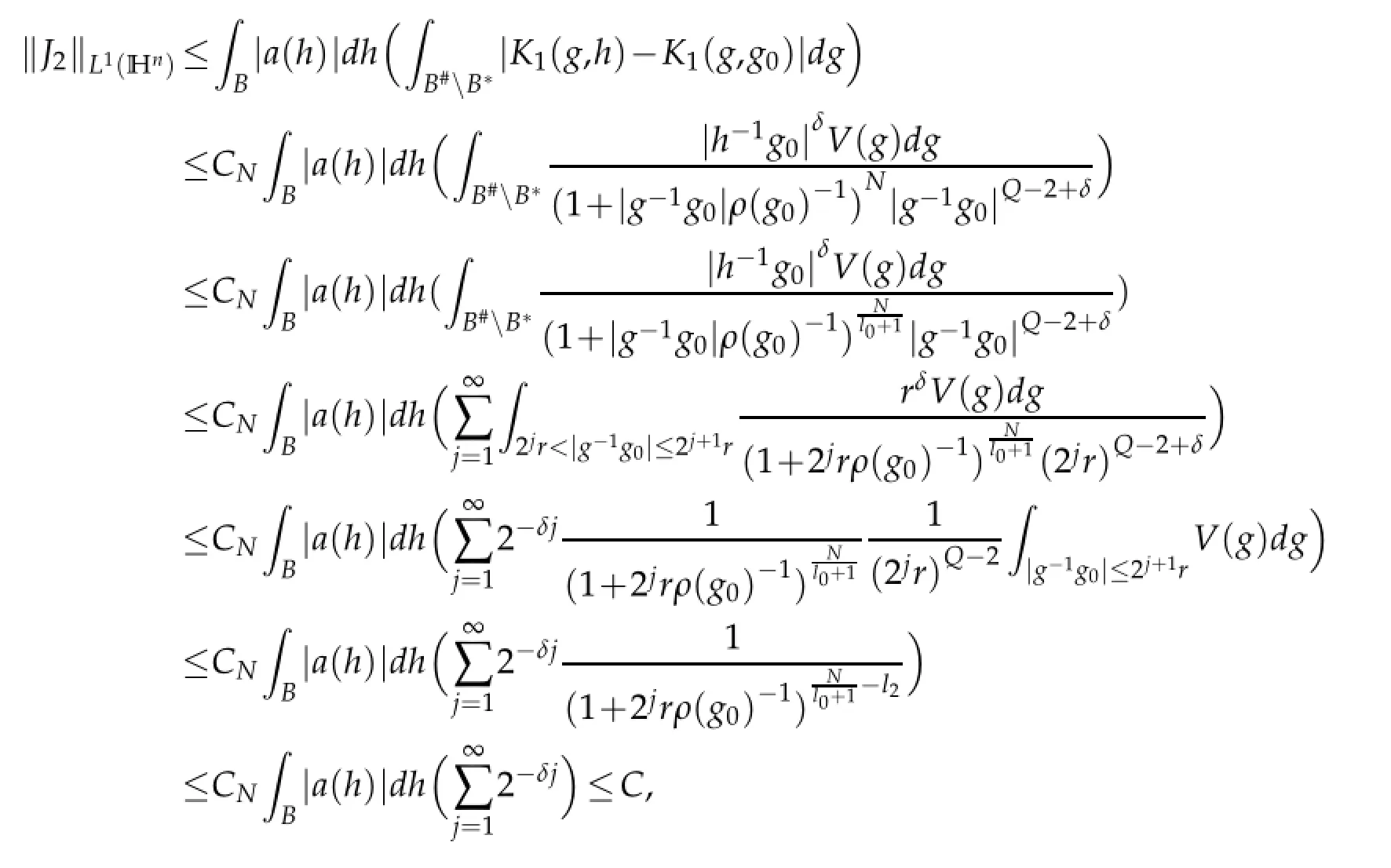
where we choose N sufficiently large.Thus Lemma 4.1 is proved.

We also arrive at the proof of Theorem 5.2 by the following Lemma.

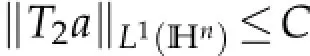
Proof.Assumethatsuppa⊆B(g0,r).Wedividedintotwocasesfortheproofofthelemma:and

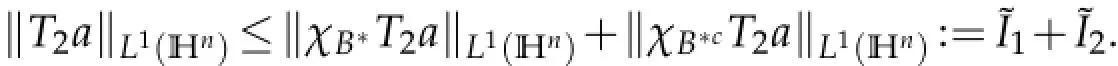
We choose appropriate q＞1 such that 1＜q＜2q1.Then according to Proposition 4.2,T2is bounded from Lq(Hn)to Lq(Hn).So similar to the proof of Case 1 in Lemma 4.1,it is easy to see that

where we choose N sufficiently large and use the assumption

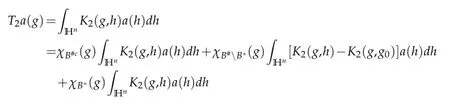
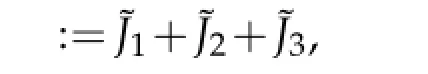
then

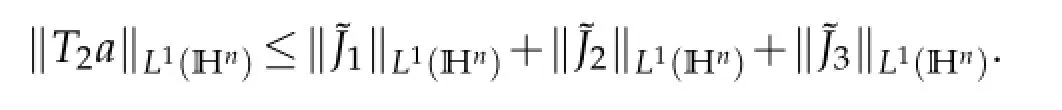
Obviously,similar to the proof of Case 1 in the proof of this lemma,we can get

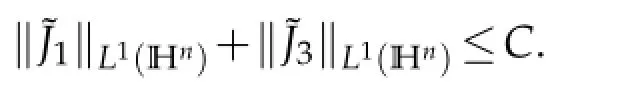
where we choose N sufficiently large.Thus this completes the proof of Lemma 4.2.

5　Results for stratified groups

In this section,we state results for stratified groups.We consistently use the same notations and terminologies as those in Folland and Stein’s book[1].

A Lie group G is called stratified if it is nilpotent,connected an⊕d sim⊕ple connected, and its Lie algebra g admits a vector space decomposition g=V1···Vmsuch that [V1,Vk]=Vk+1for 1≤k＜m and[V1,Vm]=0.If G is stratified,its Lie algebra admits a family of dilations,namely,

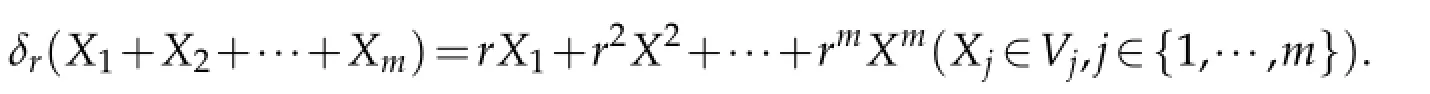
Assume that G is a Lie group with underlying manifold Rnfor some positive integer n. G inherits dilations from g:if x∈G and r＞0,we write

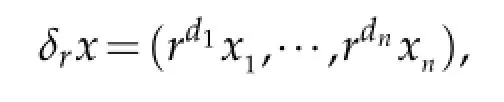
where 1≤d1≤···≤dn.The map x→δrx is an automorphism of G.The left(or right) Haar measure on G is simply dx1···dxn,which is the Lebesgue measure on g.For any measurable set E⊆G,denote by|E|the measure of E.The inverse of any x∈G is simply x−1=−x.The group law has the following form

for some polynomials p1,···,pnin x1,···,xn,y1,···,yn.

The measure of B(x,r)is

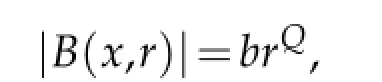
where b is a constant.

Let X={X1,···,Xl}be a basis for V1(viewed as left-invariant vector fields on G).It follows from[1]that Xj,j=1,2,···,l,are skew adjoint,that is,Letbe the sub-Laplacian on G.It follows from the definition of the stratified Lie group that the Heisenberg group is a special stratified Lie group.

The corresponding results on the stratified Lie group are given as follows:

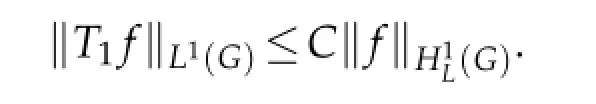
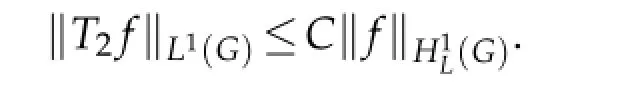
References

[1]G.B.Folland and E.M.Stein,Hardy Spaces on Homogeneous Groups,Princeton University Press,Princeton,1982.

[2]R.M.Gong,J.Li and L.Song,Besov and Hardy spaces associated with the Schr¨odinger operator on the Heisenberg group,J.Geom.Anal.,24(2014),144–168.

[3]H.Q.Li,Estimations Lpdes op´erateurs de Schr¨odinger sur les groupes nilpotents,J.Func. Anal.,161(1999),152–218.

[4]P.T.Li andL.Z.Peng,Lpboundedness of commutator operator associatedwith Schr¨odinger operators on Heisenberg group,Acta Math.Sci.Ser.B Engl.Ed.,32(2012),568–578.

[5]C.C.Lin,H.Liu and Y.Liu,Hardy spaces associated with Schr¨odinger operators on the Heisenberg group,preprint available at arXiv:1106.4960.

[6]C.C.Lin and H.P.Liu,BMOL(Hn)spaces and Carleson measures for Schr¨odinger operators,Adv.Math.,228(2011),1631–1688.

[7]Y.Liu,LpEstimates for Schr¨odinger operators on the Heisenberg group,J.Korean Math. Soc.,47(2010),425–443.

[8]Y.Liu,J.Z.Huang and D.M.Xie,Some estimates of Schr¨odinger type operators on the Heisenberg group,Arch.Math.,94(2010),255–264.

[9]Y.Liu,J.Z.Huang and J.F.Dong,An estimate on the heat kernel of Schr¨odinger operators with non-negative potentials on nilpotent Lie groups and its applications,Forum Math.,27 (2015),1773–1798.

[10]Y.Liu and W.J.Xie,Riesz transform related to Schr¨odinger type operator on the Heisenberg group,Georgian Math.J.,22(2015),397–407.

[11]E.M.Stein,Harmonic Analysis:Real-Variable Methods,Orthogonality,and Oscillatory Integrals,Princeton University Press,Princeton,1993.

[12]D.Yang and Y.Zhou,Localized Hardy spaces H1related to admissible functions on RD-spaces and applications to Schr¨odinger operators,Trans.Amer.Math.Soc.,363(2011),1197–1239.

10.4208/ata.2016.v32.n1.7

24 July 2015;Accepted(in revised version)18 December 2015

∗Corresponding author.Email addresses:liuyu75@pku.org.cn(Y.Liu),tgb0405@126.com(G.B.Tang)

Abstract.Let Hnbe the Heisenberg group and Q=2n+2 be its homogeneous dimension.In this paper,we consider the Schr¨odinger operator−∆Hn+V,where∆Hnis the sub-Laplacian and V is the nonnegative potential belonging to the reverse H¨older class Bq1for q1≥Q/2.We show that the operatorsand T2=are both bounded fromOur results are also valid on the stratified Lie group.