板翼动力锚沉贯深度模型试验研究

韩聪聪，刘 君, 2

(1.大连理工大学 水利工程学院，辽宁 大连 116023；2.大连理工大学 海岸与近海工程国家重点实验室，辽宁 大连 116023)

板翼动力锚沉贯深度模型试验研究

韩聪聪1，刘 君1, 2

(1.大连理工大学 水利工程学院，辽宁 大连 116023；2.大连理工大学 海岸与近海工程国家重点实验室，辽宁 大连 116023)

板翼动力锚是依靠自重完成安装并靠自重和海床土的抗力来锚固的新型动力锚。板翼动力锚高速(15～25 m/s)贯入地基过程中涉及到高应变率、流固耦合、土体软化和大变形等难题，模型试验可避免上述计算困难，能直接得出不同的贯入速度所对应的沉贯深度。本文首先推导了模型相似关系，然后在常规重力条件下，进行了两组26个工况的板翼动力锚在均质黏土中动力安装过程的模型试验，根据试验结果确定了率效应参数的取值范围，并研究了每一项受力对沉贯深度的影响。最后提出了在均质黏土中预测板翼动力锚沉贯深度的经验公式。

动力锚；锚-土相互作用；板翼动力锚；模型试验；沉贯深度

通迅作者：刘 君。E-mail：junliu@dlut.edu.cn

Abstract：Gravity installed plate anchors are newly developed dynamic anchors installed through self-weight.The uplift capacity is provided by the anchor’s self-weight and the soil resistance.The installation process is a high-speed motion (15～25 m/s) which involves computational problems such as the fluid-solid interaction,the stain-softening and strain-rate behavior of soil and large deformation of soil.In order to avoid the problems mentioned above,the similitude requirements in normal gravity field are discussed firstly,then the results from two groups of penetrating model tests are presented to study the relation between penetration velocity and embedment depth in uniform clay.According to the test results,the ranges of the parameter characterizing the strain-rate effect are obtained.The effects of each part in the motion equation on the embedment depth are also discussed.An empirical equation is finally presented to estimate the embedment depth in uniform clay based on the anchor energy.

Keywords：dynamic anchors; anchor-soil interaction; gravity installed plate anchors; model test; embedment depth

海底蕴含丰富的石油天然气资源。随着近海能源的不断开采耗竭，人们逐渐将目标转向深海[1]。在深海(水深>300～500 m)工程中，采用浮式结构比固定式结构更经济[2]。浮式结构通过锚链与嵌入海床中的锚连接，依靠锚周围土体的抗力提供抗拔承载力，平衡上部结构传递的荷载[3]。适用于深海工程的锚主要有：法向承力锚(Vertical loaded anchors)、吸力式沉箱(Suction caissons)、吸力式安装平板锚(Suction embedded plate anchors)和动力安装锚(Dynamically installed anchors)[4]。

动力安装锚是深海工程中的新型锚[5]，安装时不需借助外力，仅需将锚释放至海床上部预定高度处，然后松开安装锚链，动力锚在水中自由下落并贯入土中一定深度。动力锚主要包括两种：鱼雷锚(Torpedo anchors)和板翼动力锚(Gravity installed plate anchors)，如图1所示。板翼动力锚和鱼雷锚有较大区别[6]：(I)板翼动力锚主要由三个大一点的尾翼和三个小一点的前翼组成；(II)在前后翼之间有一个可以绕中轴360度旋转的加载臂，锚链连接在加载臂顶端的锚眼处。当上拔角度(锚眼处锚链与水平面夹角)合适时，锚具有下潜的特性[6,7]，因此能提供更高的承载力并能防止锚体被拔出。

图1 两种形式的动力锚Fig.1 Two types of dynamically installed anchors

动力锚的安装过程分两个阶段：在水中的自由下落阶段和在土中的沉贯阶段。本文仅关注第二阶段。目前关于鱼雷锚沉贯过程的研究比较多，主要以离心模型试验[3,5,8-11]为主。当贯入速度为20 m/s时，锚尖端埋深比(锚尖端入土深度与锚的总高度之比)为2～3。板翼动力锚方面，Zimmerman等[12]在墨西哥湾进行的54组现场试验得到的平均埋深比为1.8。Gaudin等[13]在轻微超固结高岭土和正常固结钙质土中分别进行了离心模型试验，当贯入速度为23 m/s时，在两种土中的埋深比分别为1.9和1.2。Cenac[14]在常规重力条件下用1/24模型锚进行了动力沉贯试验，当贯入速度为5～7 m/s时，埋深比为1.5～2.1。

动力锚到达土表面时的贯入速度越大，对应的沉贯深度越大，提供的抗拔力也越高。板翼动力锚是一种新型的动力锚，沉贯深度的研究成果还非常有限。本研究首先分析了各项作用力对锚沉贯深度的影响，然后讨论了常规重力场模型试验的相似关系，进而开展了两组不同速度水平的26个板翼动力锚在均质黏土中动力安装过程的模型试验，得到了不同贯入速度和对应的沉贯深度，确定了模型试验中率效应参数的取值范围，最后提出了预测板翼动力锚沉贯深度的预测模型。

1 试验准备

1.1土样的制备

本试验用高岭土(Spes-white-kaolin clay)模拟海洋黏土。高岭土的基本特性为：比重Gs=2.61，液限Ll=65%，塑限Lp=34%。首先将高岭土与水按重量比1∶1.3(2倍液限含水量)混合，放入搅拌机中真空搅拌5小时，确保掺杂在泥浆中的气体完全排出；然后将搅拌好的泥浆放入试验箱(试验箱内部尺寸：长×宽×高=600 mm×220 mm×800 mm)中加压固结，得到均质土样。

1.2模型锚

模型锚的几何尺寸如图2所示，图中单位为mm。除加载臂部分外，两种模型锚的尺寸一致，质量分别为9.5和8.8 g。为了便于模型加工，翼板部分进行了加厚处理，所以对应原型锚重量分别为745和690 kN，比实际工程中所用锚的重量380 kN大。

1.3锚在土中的受力

沉贯过程中，作用在锚上的力有：锚在水中的有效重量Ws，锚受到土的浮力Fb，土对锚的端承阻力Fbear和摩擦阻力Ffrict，拖曳阻力Fd。锚的受力如图3所示。

1) 端承阻力Fbear和摩擦阻力Ffrict：Fbear为锚在垂直于轴线方向截面上受到的土阻力，如式(1)所示。其中：Nc为承载力系数，可按深埋条形基础取为7.5[15]，与文献[8,11,13]在计算鱼雷锚尾翼和板翼动力锚的端承阻力时相同；su为土的不排水抗剪强度；At为锚在垂直轴线方向与土的接触面积。

Fbear=NcsuAt

(1)

Ffrict为锚的侧面受到的土阻力，如式(2)所示。其中，α为锚土界面间的摩擦系数，通常取为土灵敏度系数St的倒数，本试验用土的灵敏度系数采用T形贯入仪的循环试验测得St=2.5～3.0，取α=0.35；As为锚侧面与土接触的面积。

Ffrict=αsuAs

(2)

2) 拖曳阻力Fd：土对锚的拖曳阻力Fd可由式(3)计算。

(3)

式中：Cd为拖曳系数，与流体的粘滞系数、运动物体的尺寸和形状有关；ρs为土的密度；Ap为锚在垂直于轴线平面上的投影面积；vt为锚在任意时刻的速度。Øye和Richardson[16,17]给出了不同形式鱼雷锚对应的Cd，认为鱼雷锚形状越复杂对应的Cd越大。参考True[18]给出的结论，本文取Cd=1.0。

图2 模型锚及尺寸Fig.2 Model anchors and dimensions

图3 锚在土中的受力示意 Fig.3 Forces acting on the anchor in soil

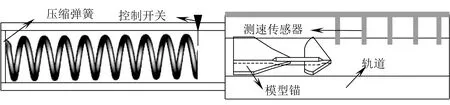
图4 发射和测速装置示意Fig.4 Schematic of the release device and the velocity measurement device

1.4相似关系

动力锚依靠在水中下落时获得的动能和自身重力势能贯入海床中，锚的自重起主要作用，所以按照弗劳德(Froude)准则设计试验，弗劳德数Fr如式(4)所示。

(4)

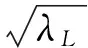
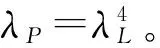
表1 模型试验和原型对应的比尺关系Tab.1 The scale ratios between model tests and prototype tests

本试验的后续试验为离心模型试验，为方便比较试验结果，本模型的几何比尺参照离心模型试验的比尺取为λL=200。综合前言部分引用的参考文献，假设原型对应的贯入速度和土的不排水抗剪强度分别为v=25 m/s，su=20 kPa。若严格按照相似关系设计模型试验，则模型试验中对应的贯入速度和土的不排水抗剪强度分别为(v)m=1.77 m/s，(su)m=0.1 kPa。当土很软时，不仅强度很难准确测量，而且土在自重作用下会继续固结，影响试验结果分析。所以模型试验中的土强度不能按照相似关系直接折减，而要适当提高。为了使模型锚仍能贯入土中，需增大锚的贯入速度。此时的相似关系如表1的第4行所示。这样在模型试验中，锚在土表面时的动能和重力势能(锚在土表面相对安装深度处的势能)的比值就比原型大，从而减弱了重力势能对沉贯深度(z)m(如图3所示)的影响，以致在本试验中，重力的影响与土的阻力相比可以忽略了。

模型试验中，浮力(Fb)m和拖曳阻力(Fd)m对(z)m的影响较小，后面会进一步分析。所以，沉贯过程中，锚的动能与土阻力对锚做的负功相等，如式(5)所示。

(5)

Fbear做的功由式(6)确定。当z小于锚前翼斜边的高度hff时，受力面积随z线性增加；当z超过hff时，受力面积不再改变。

(6)

式中：a=NcAt，d=NcAthff。对于模型锚，(a)m=Nc(At)m，(d)m=Nc(At)m(hff)m。

Ffrict做的功由式(7)积分而得。由于锚的形状比较复杂，可将锚沿高度方向平均分成n份，每一份的高度为Δh=h/n。第i份表示的是从锚尖端向上数的第i个微元，对应的侧面积和沉贯深度分别为(Ai)s和(z-iΔh)，如图3所示。

(7)

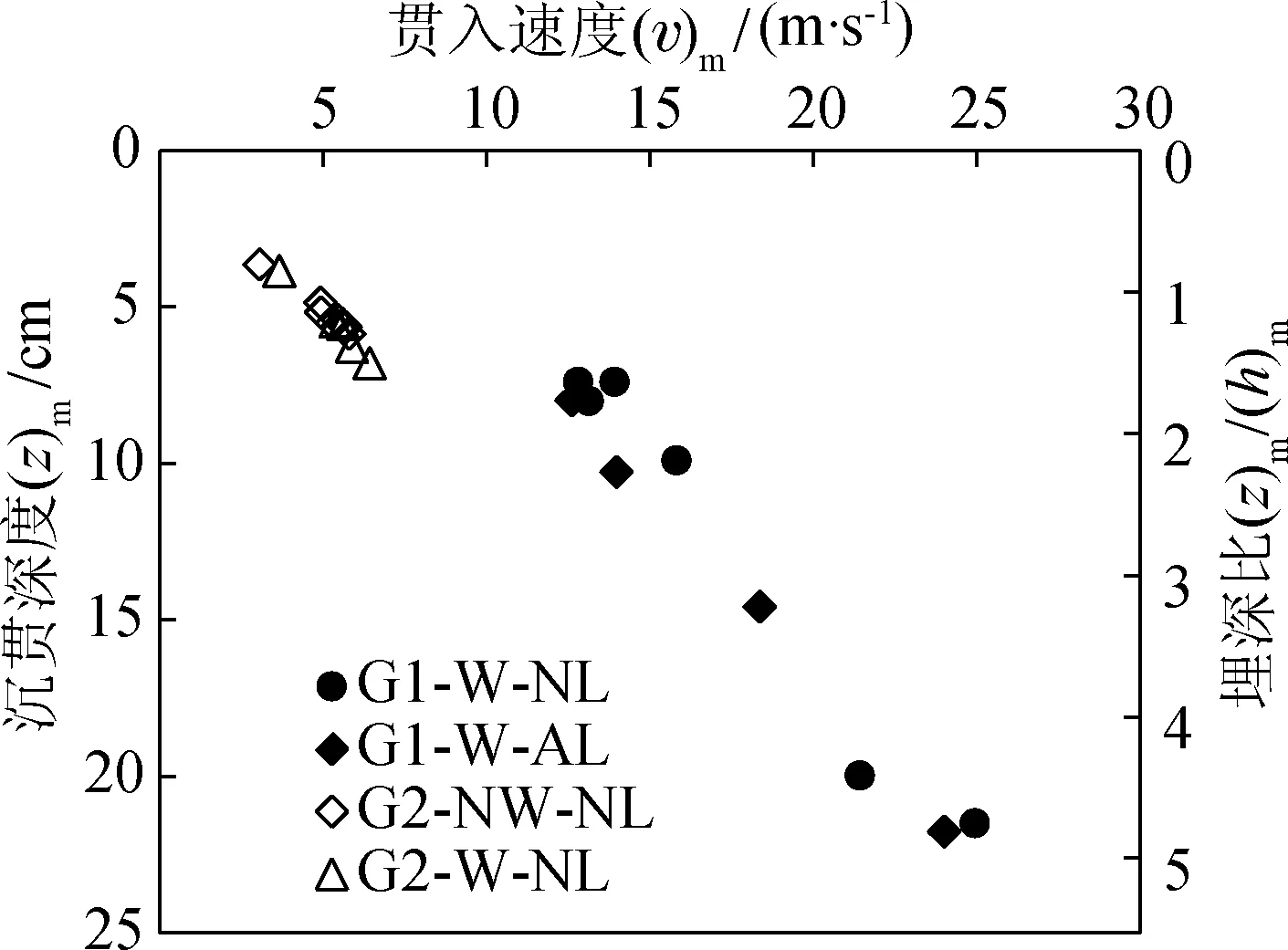
式中；b=∑α(Ai)s，c=∑α(Ai)siΔh。当z>h时，k=n，参数b和c为常量；当z

将式(6)、式(7)代入式(5)，再用式(5)分别计算原型和模型对应的功能关系，二者相比就可得到沉贯深度比尺λz，如式(8)所示。

(8)

1.5试验装置

本试验主要考虑沉贯过程中锚-土相互作用，不考虑锚在水中的自由下落过程。所以，锚在水中自由下落获得的动能由图4所示的发射装置提供。该装置利用压缩弹簧撞击锚，使锚获得动能。通过调节弹簧的压缩量来改变模型锚的初始贯入速度。为保证锚的直线运动和测量锚的速度，在发射装置的前端安置了轨道，在轨道上面布设测速传感器来测量锚的速度。

2 贯入试验结果及分析

本文共进行两组模型试验，第一组为高速贯入试验((v)m=12.60～24.94 m/s)，第二组为低速贯入试验((v)m=3.05～6.42 m/s)。用T形贯入仪或球形贯入仪测量(su)m，贯入速率为1 mm/s。测得两组试验土样的(su)m分别为2.4和1.2 kPa。为避免边界效应的影响，应使贯入仪到侧壁的距离≥(3～5)R，其中R为贯入仪半径。综合考虑试验箱的内部尺寸及贯入仪测点位置，两组试验点布置如图5所示，图中单位为mm。其中实心圆点表示球形贯入仪测点位置，实心矩形表示T形贯入仪测点位置，Y形部分表示模型锚贯入点位置。

图5 试验点布置Fig.5 Layout of the model tests

第一组试验土表面有50 mm深的水层，前6次试验模型锚无加载臂且不带锚链；后5次试验有加载臂并带锚链，锚链用直径为0.23 mm的鱼线模拟。其中9点位置处没有测到锚的出口速度，共有10个可用工况。第二组试验模型锚无加载臂，不带锚链，前10次试验土表面无水，后5次试验土表面有50 mm深的水层。其中2点和5点位置处锚没有垂直贯入土中，共有13个可用工况。两组试验工况结果列于表2。

表2 模型试验工况Tab.2 The cases of the model tests

注：G1-W-AL 表示第一组试验，有水有加载臂的工况;G2-NW-NL表示第二组试验，没有水，没有加载臂的工况。

2.1动力沉贯试验结果

锚尖端的沉贯深度(z)m与贯入速度(v)m之间的试验结果如图6所示。从图中可以看出，沉贯深度(z)m随(v)m的增加而增大，符合一般常识。第一组试验中，当(v)m相同时，有加载臂和锚链的深度(z)m稍大一些，因为其质量比较大，提供的动能也大。第二组试验中，土表面是否有水对(z)m影响不大。

2.2沉贯深度的解析分析

沉贯深度z可采用式(9)所示的基于牛顿第二定律所建立的微分方程[18]来计算。

(9)

式中：Rfb、Rff分别为端承项和摩擦项对应的率效应参数。土的率效应是指su随剪应变率增大而提高的现象。Rf可采用式(10)所表示的指数形式[19]。

(10)

图6 模型试验的贯入速度及对应的沉贯深度Fig.6 Anchor embedment depth vs.velocity in model tests

图7 模型试验结果(原型)与解析解对比Fig.7 The comparison between model test and analytical results

下面分别讨论模型试验中各项阻力对沉贯深度的影响。

1) 锚的有效重量(Ws)m和所受浮力(Fb)m对(z)m的影响

在低速贯入试验中，(v)m=3.05～6.42 m/s，对应的(z)m= 36.58～68.25 mm，动能与势能的比为15.6～32.8。对于高速贯入模型试验，二者的比值更大。所以(Ws)m对(z)m的影响较小，可忽略不计。同理，(Fb)m对(z)m的影响也可忽略不计。

2) 拖曳阻力(Fd)m对(z)m的影响

当(v)m=25 m/s时，用式(9)计算考虑(Fd)m比不考虑时对应的(z)m偏小不到10%。

综上所述，在推导相似关系时，可不考虑(Ws)m、(Fb)m和(Fd)m对(z)m的影响，锚的动能全部转化为动力沉贯时克服土阻力做的功。这是相似关系式(8)成立的前提条件。

3) 端承阻力(Fbear)m和摩擦阻力(Ffrict)m对(z)m的影响

当锚刚贯入土中时，只有尖端部分进入土中，与土接触的侧面积很小，所以端承项所占比例很大。随着锚继续向下运动，锚和土之间的接触面积增大，摩擦项所占比例逐渐增加。当锚全进入土中后，摩擦阻力是端承阻力的2.6倍。

4) 土的率效应对(z)m的影响

采用不同的β值，在不考虑(Ws)m、(Fb)m和(Fd)m时，用式(8)可计算出(v)m与(z)m之间的关系。当β分别取0.17和0.14时与两组试验点吻合最好。第一组试验的β值比第二组的大，说明β的取值与贯入速度有关，这与文献[8]中的结论一致。

2.3由模型试验向原型的换算

如果原型锚的速度和地基土的强度分别为v=25 m/s,su=20 kPa，第一组模型试验的速度比尺λv=1，土强度比尺λsu=8.33；第二组模型试验的λv=4，λsu=16.67。由相似关系式(8)可得原型锚沉贯深度zp。在相同率效应参数前提下，用式(9)也可以计算出原型锚在不考虑Ws、Fb和Fd时不同的v对应的沉贯深度zd，zp和zd的比较如图7所示。从图7可以看出，模型试验结果和理论计算结果非常接近，除工况G2-NW-NL2，其余工况最大偏差不超过7%。由于模型试验低估了重力势能的影响，所以模型试验的沉贯深度比实际情况低。这可以在式(9)中将锚的自重Ws和浮力Fb考虑进来，进而可以修正模型试验结果，如表3所示。从表3可知，当v相同时，率效应越大，Ws和Fb对z的影响越小，且z的提高幅度随着v的增加而减小。

表3 两种情况下原型的沉贯深度Tab.3 The embedment depths in two cases in prototype scale

2.4预测沉贯深度的经验公式

影响锚沉贯深度z最主要的因素有锚的质量m、贯入速度v、土的不排水抗剪强度su、锚的侧面积As和有效直径deff(与锚的投影面积相等的圆的直径)。综合上述因素，依据模型试验结果，本文给出了一个在均质黏土中估计锚沉贯深度的经验公式：

(11)

式中：Etotal为锚的总能量，η、r是与土性质、锚的形式、尺寸、质量、贯入速度等有关的系数。当式(11)中η和r分别取1.54和0.63时，与试验结果偏差最小，如图8所示。

3 讨 论

3.1是否有水对沉贯深度的影响

沉贯过程中，锚土界面间会有水进入，这部分水起润滑作用，会使(Ffrict)m减小。所以，当(v)m相同时有水模型试验得到的(z)m应比无水时大。从图6中可知，是否有水对(z)m几乎没有影响。这可能是由于当锚从空气进入水中时有一个锚-水碰撞过程，有水花溅起，会消耗一部分动能。因此，锚的实际贯入速度(v)m应比测速传感器测到的出口速度小，这部分由于能量消耗造成(z)m的减小和由水的润滑作用抵消，所以本试验有水与否对(z)m几乎没有影响。Ffrict是影响z的最重要因素之一，有必要进一步研究水的润滑作用对沉贯深度的影响。

3.2锚在沉贯时周围土体流动机制

在原型或现场测试中，沉贯时间会持续1～2 s，同时随着沉贯深度的增加，锚周围土体的应力水平也随之提高，土更容易回流。要深入研究沉贯过程中锚周围土体的流动机制需要结合数值分析的结果。

3.3率效应对沉贯深度的影响

模型试验的剪应变率比原型高，所以对应的率效应比原型大。另外，率效应参数β与贯入速度v有关，β随v的增加而增大。综合两方面的影响，模型试验中的率效应比原型中显著，这个问题也存在于离心模型试验中。O’Loughlin等[8]认为由于率效应的影响，通过模型试验换算到原型的沉贯深度z比实际低40%左右。

为了验证经验公式的可行性，需要将其和现场实测结果或满足相似关系的模型试验结果进行对比。Cenac[14]的模型长度比尺为24，将锚分别从距离土表面1.2、1.5及1.8 m的高度处静止释放，贯入由砂土和膨润土混合而成的泥浆中，泥浆的平均不排水抗剪强度为su=0.78 kPa。经验公式(11)的预测结果与Cenac的试验结果对比如图9所示。文献[14]的试验结果比本文预测结果高20%～38%，预测结果偏低的原因有两点：1) 式(11)的预测结果是基于本次模型试验得到的，低估了重力势能对z的影响；2) 本次模型试验中的率效应比Cenac的大，当v相同时对应的z偏小。所以经验公式(11)的预测结果偏于保守。

现场试验测得β=0.04～0.08[21,25]，以β=0.06为例，用式(9)可以计算不同的v及对应的z，拟合得到式(11)中的参数η和r分别为1.93和0.71，此时预测的结果与文献[14]中的试验结果吻合很好，如图9所示。

图8 基于总能量预测锚的沉贯深度Fig.8 Prediction for embedment depth based on energy equation

图9 预测结果与Cenac试验结果对比Fig.9 Prediction for embedment depth of the model tests by Cenac[14]using the empirical equation

4 结 语

本文在常规重力场下开展了板翼动力锚在均质黏土地基中动力沉贯模型试验，得出以下结论：

1) 对应两组模型试验，率效应参数β分别取0.17和0.14，随贯入速度的增加而增大，表明率效应参数与剪应变率有关。

2) 贯入过程中，锚中间缺口和顶部的土体不会回流，所以只有锚的尖端部分受端承阻力作用。

3) 在本文模型试验中，由于低估了锚的重力势能对沉贯深度的影响，所以由相似关系换算到原型的沉贯深度偏低20%～30%左右。

4) 基于模型试验的结果提出了在均质黏土地基中预测锚沉贯深度的经验公式，由于模型试验率效应大，且低估了重力势能对沉贯深度的影响，所以用经验公式预测的沉贯深度偏于保守。

[1] RANDOLPH M F,GAUDIN C,GOURVENEC S M,et al.Recent advances in offshore geotechnics for deep water oil and gas developments [J].Ocean Engineering,2011,38(7)：818-834.

[2] RONALDS B F.Deepwater facility selection[C]//Offshore Technology Conference.2002,OTC14259.

[3] RICHARDSON M D,O’ LOUGHLIN C D,RANDOLPH M F,et al.Setup following installation of dynamic anchors in normally consolidation clay[J].Journal of Geotechnical and Geoenvironmental Engineering,2009,135(4)：487-496.

[4] 国振，王立忠，李玲玲.新型深水系泊基础研究进展[J].岩土力学,2011,32(S2)：469- 477.(GUO Zhen,WANG Li zhong,LI Ling ling.Recent advances in research of new deepwater anchor foundations [J].Rock and Soil Mechanics,2011,32(S2)：469-477.(in Chinese))

[5] O’ LOUGHLIN C D,RANDOLPH M F,RICHARDSON M.Experimental and theoretical studies of deep penetrating anchors[C]//Offshore Technology Conference.2004,OTC16841.

[6] SHELTON J T.OMNI-MaxTM anchor development and technology[C]//OCEANS 2007.IEEE,2007：1-10.

[7] LIU J,LU L,YU L.Large deformation finite element analysis of gravity installed anchors in clay[C]//Proceedings of the 33rd International Conference on Ocean,Offshore and Arctic Engineering.2014.

[8] O’LOUGHLIN C D,RICHARDSON M D,RANDOLPH M F.Penetration of dynamically installed anchors in clay [J].Géotechnique,2013,63(11)：909-919.

[9] O’LOUGHLIN C D,RICHARDSON M D,RANDOLPH M F.Centrifuge tests on dynamically installed anchors[C]//ASME 2009 28th International Conference on Ocean,Offshore and Arctic Engineering.2009：391-399.

[10] HOSSAIN M S,O’LOUGHLIN C D,KIM Y.Dynamic installation and monotonic pullout of a torpedo anchor in calcareous silt [J].Géotechnique,2015,65(2)：77-90.

[11] HOSSAIN M S,KIM Y,GAUDIN C.Experimental investigation of installation and pullout of dynamically penetrating anchors in clay and silt [J].Journal of Geotechnical and Geoenvironmental Engineering,2014,140(7)：04014026.

[12] ZIMMERMAN E H,SMITH M W,SHELTON J T.Efficient gravity installed plate anchors for deepwater mooring [C]// Offshore Technology Conference.2009,OTC20117.

[13] GAUDIN C,O’LOUGHLIN C D,HOSSAIN M S,et al.The performance of dynamically embedded anchors in calcareous silt [C]//ASME 2013 32nd International Conference on Ocean,Offshore and Arctic Engineering.2013.

[14] CENAC W I.Vertically loaded anchor：drag coefficient,fall velocity,and penetration depth using laboratory measurements [D].Texas A&M University,Texas.2011.

[15] SKEMPTON A W.The bearing capacity of clays [C]// Building Research Congress.1951：180-189.

[16] Øye I.Simulation of trajectories for a deep penetrating anchor [R]//Report No.250：2000.Trondheim,Norway：CFD Norway.2000.

[17] RICHARDOSN M D.Dynamically installed anchors for floating offshore structures [D].The University of Western Australia,Crawley,Australia.2008.

[18] TRUE D G.Undrained vertical penetration into ocean bottom soils [D].University of California：Berkeley,California.1976.

[19] EINAV I,RANDOLPH M.Effect of strain rate on mobilized strength and thickness of curved shear bands [J].Géotechnique,2006,56(7)：501-504.

[20] BISCONTIN G,PESTANA,J M.Influence of peripheral velocity on vane shear strength of an artificial clay [J].Geotechnical Testing Journal,2001,24(4)：423-429.

[21] STEINER A,KOPF A J,L’HEUREUX J S,et al.In situ dynamic piezocone penetrometer tests in natural clayey soils-a reappraisal of strain-rate corrections [J].Canadian Geotechnical Journal,2013,51(3)：272-288.

[22] DAYAL U,ALLEN J H.The effect of penetration rate on the strength of remolded clay and sand samples [J].Canadian Geotechnical Journal,1975,12(3)：336-348.

[23] CHOW S H,O’LOUGHLIN C D,RANDOLPH M F.Soil strength estimation and pore pressure dissipation for free-fall piezocone in soft clay [J].Géotechnique,2014,64(10)：817-827.

[24] MORTON J P,O′LOUGHLIN C D,WHITE D J.Strength assessment during shallow penetration of a sphere in clay[J].Géotechnique Letters,2014,4：262-266.

[25] LEHANE B M,O′LOUGHLIN C D,GAUDIN C,et al.Rate effects on penetrometer resistance in kaolin[J].Géotechnique,2009,59(1)：41-52.

Model tests on the penetration depth of gravity installed plate anchors

HAN Congcong1,LIU Jun1,2

(1.School of Hydraulic Engineering,Dalian University of Technology,Dalian 116023,China；2.State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian 116023,China)

P751

A

10.16483/j.issn.1005-9865.2016.05.011

1005-9865(2016)05-0092-09

2015-09-23

国家自然科学基金资助项目(51479027;51539008)

韩聪聪(1990-)，女，河北石家庄人,博士研究生，主要从事海洋岩土工程研究。