基于小波分析的海洋平台实时结构健康监测
2016-10-12李晔
李 晔
(中国船级社 海工技术中心,天津 300457)
基于小波分析的海洋平台实时结构健康监测
李 晔
(中国船级社 海工技术中心,天津 300457)
由于海洋平台结构长期处于恶劣的海洋环境中,并受到各种载荷的交互作用,结构容易产生各种形式的损伤。因此,对海洋平台进行实时监测有着十分重要的现实意义。以单筒简易导管架平台为例,主要在结构损伤的判定和定位两方面对海洋平台的实时结构健康监测进行研究,结果表明通过对结构响应信号进行小波分析,小波变换系数和小波包能量分布可以很好地定义损伤识别指标。
海洋平台;损伤识别;小波变换;小波包分解
Abstract:Due to severe ocean environment,offshore structures are easy to be influenced or damaged by complex environmental loadings.Therefore,it is very important to implement on-line structural health monitoring for offshore structures.Taking a simple jacket platform as an example,this paper presents a study on damage detection and localization of offshore structures.By wavelet analysis of structural response data,it is shown that wavelet transform coefficients and wavelet packet energy can accurately detect damage conditions.
Keywords:offshore structure; damage detection; wavelet transform; wavelet packet decomposition
海洋平台长期服役在恶劣的海洋环境中,并受到各种载荷的交互作用,如风载荷、海流、波浪载荷、冰载荷等,有时还要受到地震、台风、海啸、船只碰撞等意外打击,结构本身还要遭到环境腐蚀、地基土冲刷等影响作用,一旦发生事故,不仅会给海洋环境造成很大的污染,还会带来不可估量的经济损失和人员伤亡,造成不好的社会影响。欧进萍等[1]开发了“海洋平台结构实时安全监测系统”应用软件,该系统于1998~1999年和1999~2000年冬季在渤海JZ20-2MUQ平台上试运行。我国对于海洋平台的实时结构健康监测处于初步研究阶段,在2001年起实施的国家“863”计划中设立了“海洋平台结构的实时监测技术”,对海洋平台的系统识别及健康监测技术进行立项研究,并已成为一项刻不容缓的重要课题。
对海洋平台的结构健康监测始于20世纪70年代,研究主要以频率和振型作为识别依据[2-4]。Kim和Stubbs[5]将平台结构单元的模态应变能变化作为损伤定位指标,李华军等[6]进一步将模态应变能分解成拉压和弯曲两种形式从而改进了传统的基于模态应变能的损伤识别方法,在此基础上李华军等[7]提出了基于交叉模态(CMCM)的结构损伤诊断方法可以识别出损伤的位置和程度,李华军等[8]提出了结合CMCM和Guyan模型缩阶的迭代模型修正方法。基于模态分析的方法在实际测量中具有一定的局限性,如测点多,测量精度低等。随着现代信号处理技术的发展,基于数据分析的结构健康监测技术得到越来越多的重视,其中小波分析方法是一个重要的研究分支,它可以对非线性、非稳性信号在时频域进行双重定位,从而更深入地剖析信号的内部特征,可以应用于地震、风、海洋工程等相关测量数据的分析[9],也被应用于一些结构损伤识别领域;Hou等[10]通过观察小波变换系数来确定疲劳造成结构损伤的发生;Sun和Chang[11]指出小波包能量分布的变化可以作为结构损伤识别的重要指标;Peng等[12,13]提出基于小波包能量的管道悬跨估算方法,在数值模拟的基础上还进行了模型实验验证。
本文研究小波分析在海洋平台的实时结构健康监测中的应用,主要运用小波变换与小波包分解对结构响应数据进行分析,从而确定结构损伤的发生时间与发生位置。利用ANSYS软件建立海洋平台的有限元模型并进行瞬态动力分析,数值模拟不同的损伤情况,然后对损伤前后的结构响应数据导入MATLAB进行小波分析,进而确立敏感的损伤识别指标。
1 建立海洋平台有限元模型
单筒简易导管架平台结构简单,成本低且施工方便,被广泛应用于海上边际油田的开发,本文以该平台结构为例,如图1所示,基本结构参数如表1所示,结构材料参数如表2所示,环境参数如表3所示。

图1 单筒简易导管架平台Fig.1 Single cylinder simple jacket platform
在ANSYS软件中建立平台结构的有限元模型,主要运用PIPE59单元和PIPE16单元对主桩、斜支撑和辅助桩建模,水下结构均采用PIPE59单元并通过WATER TABLE来施加环境载荷,并在泥线以下6倍主桩径处施加约束。平台主体简化为质量MASS21单元。通过瞬态动力分析可以计算出环境载荷下的结构响应数据,提取出相关节点处的数据作为测点响应信号,进而运用小波分析进行结构损伤识别分析。

表1 平台结构的基本参数Tab.1 Basic parameters of platform structure

表2 材料参数Tab.2 Material parameters

表3 环境参数Tab.3 Environmental parameters
2 小波变换系数奇异点确定损伤发生
小波分析是一种典型的时频域分析方法,利用可伸缩和平移的可变视窗,能够聚焦到信号的细节并且保留数据的瞬态特征。1984年法国地球物理学家Morlet引入小波变换概念对信号进行分解,并与法国理论物理学家Grassmann共同提出了将信号按一个确定函数的伸缩平移系列进行展开的理论,即小波分析理论。小波函数由尺度因子和平移因子表征,尺度因子的作用是将基本小波函数做伸缩反映信号的频率信息,平移因子表示函数在时间轴上的位置反映信号的时间信息。由于小波函数具有紧支性,它与信号数据比较,就相当于截取信号的一小部分进行比较并计算小波系数,这样小波变换具有时间局部能力,因为改变平移因子可以使小波函数在信号上沿时间轴移动得到不同时间位置处的小波系数,其中小波系数表示小波函数与信号的相似程度,小波系数越大两者越相似,而且不同尺度因子的小波函数具有不同的频率范围,小波系数的大小还反映了信号在此频率范围内的频率成分的多少。因此,小波变换系数可以提供信号数据时间和频率信息,小波变换系数也会随着结构参数的变化相应地发生一定的变化,可以用于结构损伤识别。
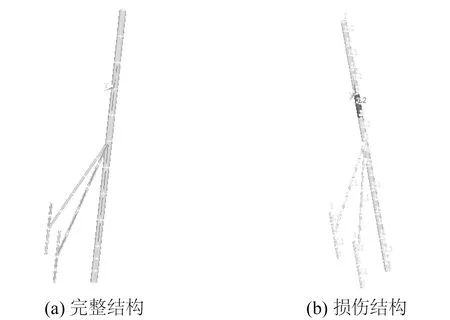
图2 海洋平台有限元模型Fig.2 Finite element model of platform
按前文所述方法在ANSYS中建立平台结构的有限元模型,原点设在静水面位置,假设损伤发生在主桩上水面以下5 m范围内,损伤情况通过改变此范围内单元的EI值来模拟,图2(a)为完整结构的有限元模型,图2(b)为损伤结构的有限元模型。
按不同的损伤程度划分为三种损伤情况:工况1为EI下降10%;工况2为EI下降30%;工况3为EI下降50%。动力响应分析的时间步长为0.05 s,总时长为50 s共计1 000步,假设第30 s时发生结构损伤情况,在ANSYS中模拟出完整结构及三种损伤情况下结构的动力响应,提取出水面处节点的结构响应数据如图3所示,其中,Signal0为完整结构,Signal1为工况1,Signal2为工况2,Signal3为工况3。
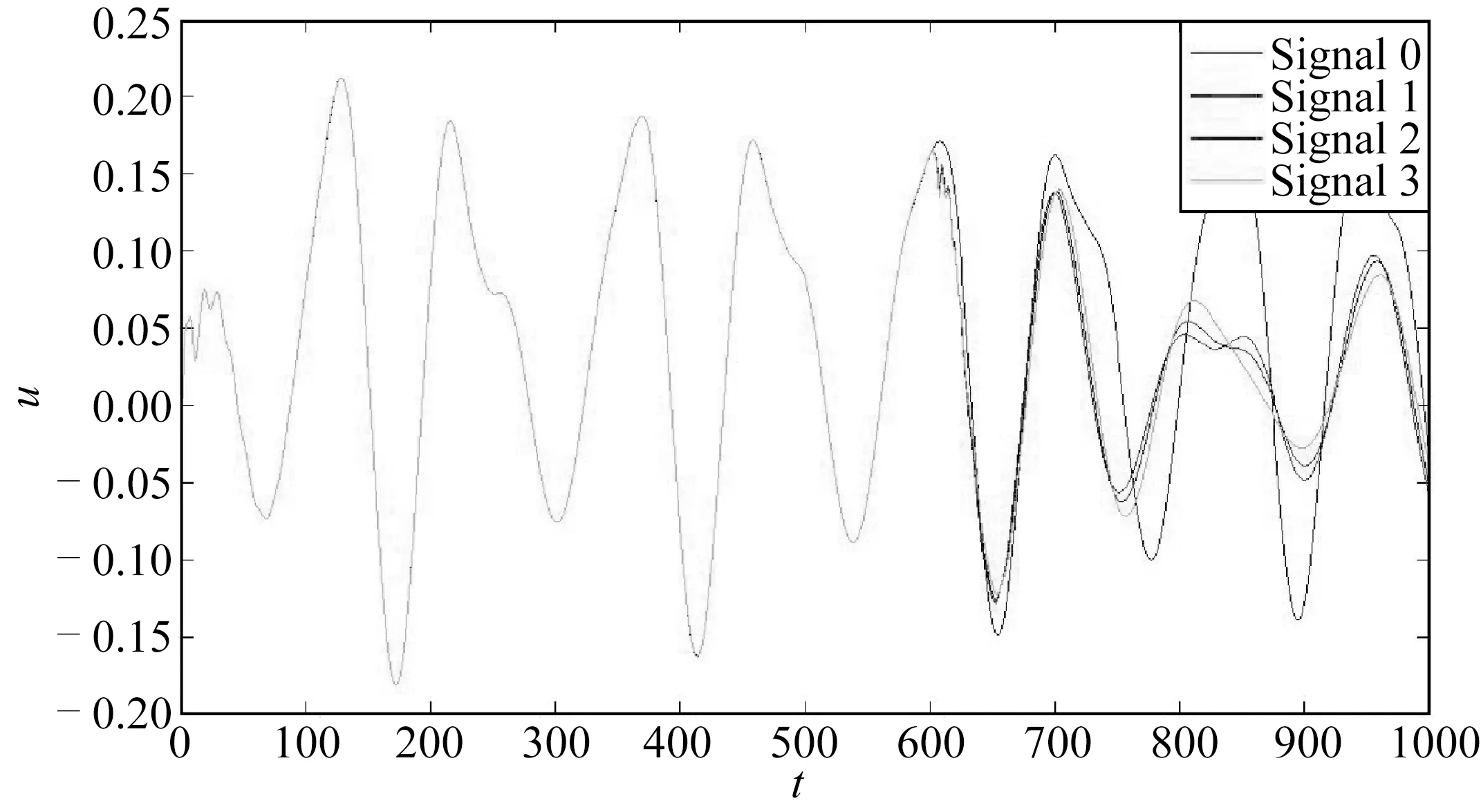
图3 不同结构情况下的结构响应信号Fig.3 Signal of structure response under different conditions
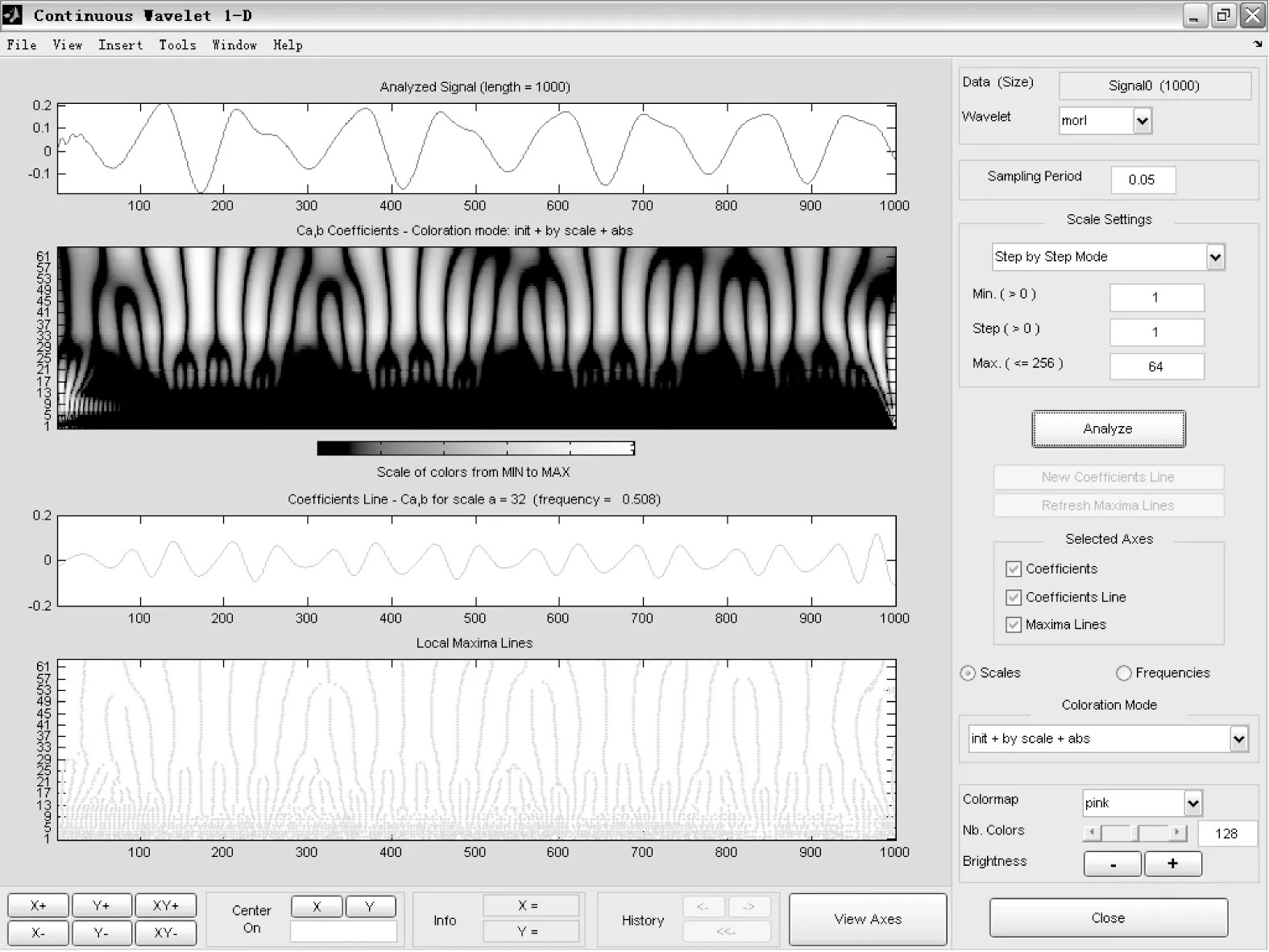
图4 结构响应数据小波分析Fig.4 Data of structure response from wavelet analysis
将提取出的不同结构情况下的响应数据导入MATLAB,采用morl小波对数据进行小波分析,图4为完整结构情况下的数据小波分析结果。对完整结构和三种损伤情况的响应数据分别进行小波分析,并提取小波变换系数,以尺度值36和4为例,如图5、图6所示。

图5 小波变换系数 (scale=36,f=0.451Hz)Fig.5 Wavelet coefficients (scale=36,f=0.451Hz)
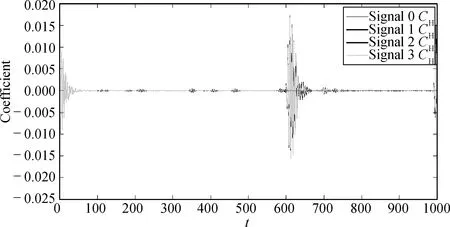
图6 小波变换系数(scale=4,f=4.063Hz)Fig.6 Wavelet coefficients (scale=4,f=4.063Hz)
图5所表示频带的中心频率为0.451Hz,图6所表示的频带的中心频率为4.063Hz,三种工况与完整结构对比,小波变换系数均在第30 s处发生变化,而且图6显示的突变比图5更加明显,因此,高频带小波变换系数的奇异点可以显著地识别出损伤发生的时间。在图6中,数据起始的高频响应是由数值模拟设置的初始条件造成的,可以忽略,只考虑稳定的动力响应部分。对于不同的损伤工况,小波变换系数的奇异点幅值随损伤程度的增大而逐渐变大,但是增幅不明显,说明奇异点对于小范围内的损伤程度变化的敏感度不高。因此,高频带小波变换系数的奇异点,可以很好地判定损伤发生的时间,而损伤程度敏感度不高。
3 小波包能量变化定位结构损伤
1992年Colifman Meyer和Wickerhause提出了小波包的概念,小波包借助小波变换在各个尺度上对每个子带都降半划分得到完全的信号频带分析,从而得到比小波变换更精细的分解。信号数据经过小波包分解后就可以计算出各个节点的能量值,即各频带的能量分布情况,结构刚度的变化引起的结构响应数据的变化会在小波包能量分布上表现出来,所以可以利用小波包能量的敏感度来进行损伤识别。
3.1小波包能量损伤识别指标
本文主要研究基于小波包能量分布的损伤特征指标包括能量变化和SAD、能量变化平方和SSD、能量比变化偏差值ERVD,定义式分别为公式(1)~公式(3):
(1)
(2)
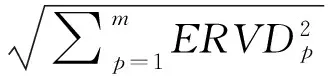
(3)
平台结构的有限元模型同前,数值模拟损伤情况为水线面以下4 m范围内主桩刚度下降50%。除平台顶与泥面处外,在主桩上自上而下间距为5 m布置8个测点,则3号测点为静水面处。在ANSYS中提取损伤前后各测点的结构响应数据,并分别导入MATLAB进行小波包分解得到各频带小波包能量分布,然后根据公式(1)~(3)计算每个测点的三种小波包能量指标值,计算结果如表4所示。
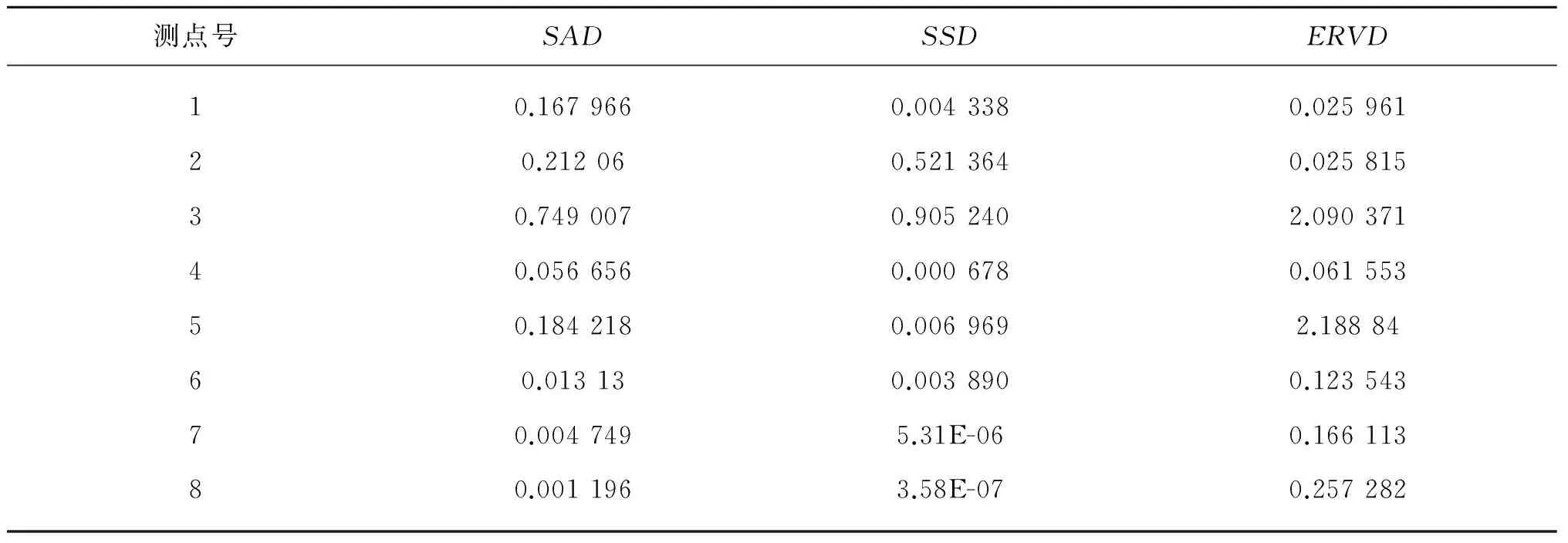
表4 小波包能量损伤指标Tab.2 Index of energy loss of wavelet package
在表2中,小波包能量损伤指标显示出损伤前后小波包能量的变化集中在水面附近的测点上,所以可以定位出损伤发生的位置。同时,水面以上的测点的指标值较大,即对于损伤的敏感度较高,从而也干扰了定位的精度,就区分度而言SAD指标可以更加显著地表明测点3(水面处)的能量变化,因此将SAD作为损伤指标进行不同损伤范围的损伤识别研究。
3.2不同损伤范围的识别结果
以水面以下主桩刚度下降50%为例,损伤范围分为4 m、2 m、1 m三种情况,分别进行结构动力响应分析并提取各个测点的结构响应数据,与完整结构的动力响应对比,运用小波包分解并计算SAD指标,为了便于对比不同损伤范围的识别情况,将SAD进行标准化:

(4)
标准化的SAD值如表5、图7所示。

表5 不同损伤范围的SADnormTab.5 SADnorm with different damage ranges
从表5可以看出,对于三种不同的损伤范围,小波包能量变化最大值均出现在测点3(水面处),即使对于1 m范围内的损伤也可以准确定损伤发生的位置,因此,SAD可以作为损伤定位指标。对比不同的损伤情况,随损伤范围变小,其他测点的干扰也随之逐渐增大,尤其是水面以上的测点,但是区分度仍在可以接受的范围之内。

图7 标准化的SAD损伤指标Fig.7 Damage index with standard SAD
4 结 语
以海洋平台结构为研究对象,提出基于小波分析的实时结构健康监测方法,主要运用小波变换与小波包分解对结构动力响应数据进行分析确定了相应的损伤识别指标。研究表明小波变换系数在高频带的奇异点可以准确识别出损伤发生的时间,小波包分解的能量分布变化可以准确定位损伤发生的位置,并提出基于小波包能量变化的SAD损伤识别指标,可以对1 m范围内的损伤准确定位。
因此,本文提出的识别方法可以准确判定及定位海洋平台结构的损伤情况,为平台实时监测提供了理论方法及技术支持,可以进一步应用于在役的海洋平台具有实际的工程指导意义。
[1] 欧进萍,肖仪清,黄虎杰,等.海洋平台结构实时安全监测系统[J].海洋工程,2001,19(2):1-6.(OU Jinping,XIAO Yiqing,HUANG Hujie,et al.Real time safety monitoring system for offshore platform structures[J].The Ocean Engineering,2001,19(2):1-6.(in Chinese))
[2] C B YUN,M Shinozuka.Identification of nonlinear structural dynamic systems[J].Journal of Structural Mechanics,1980,8:187-203.
[3] S S Sunder,R A Sanni.Foundation stiffness identification for offshore platforms[J].Applied Ocean Research,1984,6:148-156.
[4] S S Sunder,S K Ting.Flexibility monitoring of offshore platforms[J].Applied Ocean Research,1985,7:14-23.
[5] J T KIM,N Stubbs.Damage detection in offshore jacket structures from limited modal information[J].International Journal of Offshore and Polar Engineering,1995,5:58-66.
[6] H J Li,H Z Yang,S L J Hu.Modal strain energy decomposition method for damage localization in 3D frame structures[J].Journal of Engineering Mechanics,2006,132:941-951.
[7] H J Li,H Fang,S L J Hu.Damage localization and severity estimate for three-dimensional frame structures[J].Journal of Sound and Vibration,2007,301:481-494.
[8] H J Li,J R Wang,S L J Hu.Using incomplete modal data for damage detection in offshore jacket structures[J].Ocean Engineering,2008,(35):1 793-1 799.
[9] K Gurley,A Kareem.Application of wavelet transforms in earthquake,wind and ocean engineering[J].Engineering Structures,1999(21):149-167.
[10] Z Hou,M Noori,R St Amand.Wavelet-based approach for structural damage detection[J].Journal of Engineering Mechanics,2000,126:677-683.
[11] Z Sun,C C Chang.Structural damage assessment based on wavelet packet transform[J].Journal of Structural Engineering,2002,128:1 354-1 361.
[12] X L Peng,H Hao,Z X Li.Application of wavelet packet transform in subsea pipeline bedding condition assessment[J].Engineering Structures,2012,39:50-65.
[13] X L Peng,H Hao,Z X Li,et al.Fan,Experimental study on subsea pipeline bedding condition assessment using wavelet packet transform[J].Engineering Structures,2013,48:81-97.
On-line structural health monitoring of offshore structures based on wavelet analysis
LI Ye
(China Classification Society Offshore Technology Center,Tianjin 300457,China)
TE54
A
10.16483/j.issn.1005-9865.2016.05.016
1005-9865(2016)05-0131-06
2015-10-08
李 晔(1975-),男,辽宁开原人,高级工程师,主要从事海工设施设计审查及海工规范编制等工作。E-mail:liye@ccs.org.cn
