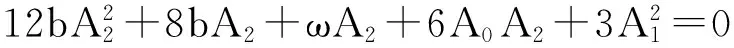G′/G-展开法的推广及其应用
2016-10-12斯仁道尔吉
斯仁道尔吉
(内蒙古师范大学数学科学学院,内蒙古呼和浩特 010022)
G′/G-展开法的推广及其应用
斯仁道尔吉
(内蒙古师范大学数学科学学院,内蒙古呼和浩特010022)
把G′/G-展开法推广到G满足椭圆方程与Riccati方程的一般情形而给出构造非线性方程精确行波解的新方法并以KdV方程为例实现了该方法.该方法还可用来求解其它的非线性方程.
G′/G-展开法;椭圆方程;Riccati方程
众所周知,扩展的tanh-函数法[1]、F-展开法[2]、G′/G-展开法[3]、辅助方程法[4]、推广的辅助方程法[5]、exp(-φ(ξ))方法[6]等都是借助某个辅助方程(组)解的展开式来求解非线性方程.例如,G′/G-展开法中函数G满足二阶线性方程
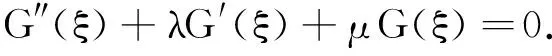
(1)
由于解的形式受到限制,不能求得非线性方程的更多类型的精确解.能否把函数G所满足的辅助方程(1)换成别的方程而建立非线性方程的多种类型的精确解呢?基于这种考虑,本文提出了把函数G所满足的辅助方程(1)换成椭圆方程和Riccati方程而求解非线性方程精确解的新方法,并以KdV方程
(2)
为例说明该方法的实现过程.
1 椭圆函数解
对KdV方程作变换u(x,t)=u(ξ),ξ=x+ωt后积分两次并置积分常数为零,则得到
(3)
令方程(3)中的u″项与3u2项相互抵消可得领头项的幂次n=2,于是可置
(4)
其中A0,A1,A2及ω为待定常数,Riccati椭圆函数w=sn(ξ,m)满足方程
(5)
这里m(0 将(4)式代入(3)式并经恒等变换cn2(ξ,m)=1-sn2(ξ,m),dn2(ξ,m)=1-m2sn2(ξ,m)以及导数关系式 变换方程后取cni(ξ,m)dni(ξ,m)snj(ξ,m)(i=0,1;j=-4,-3,-2,-1,0,1,2,3,4)的系数为零,则得到如下关于A0,A1,A2,m,ω的代数方程组 6A1A2+2A1=0, 6m2A1A2+2m2A1=0, -6m2A1A2+ωA1+6A0A1-6A1A2=0, 用Maple求解此方程组,则得如下四组解 (6) (7) (8) (9) 将(6)~(9)式同ξ=x+wt一起代入(4)式得到KdV方程的椭圆函数解 (10) (11) (12) u4(x,t)=23(m4+14m2+1+m2+1)- (13) 这里用了等式dn2(x,m)+m2sn2(x,m)=1以及sn(x,0)=sinx,cn(x,0)=cosx.显然,解(10),(11)和(12),(13)分别表示左行波与右行波.特别,在解(12),(13)中令m→0,则分别得到解(10)式和解 在解(12),(13)中令m→1,则分别得到如下解 u(x,t)=8csch22(x-16t). 现在置 (14) 其中A0,A1,A2及ω为待定常数;而f(ξ)满足Riccati方程 (15) 其解为 (16) 将(14)式代入(3)式并将f′,f″,f‴等用变换关系式 替代后令fj(j=0,1,…,8)的系数等于零,则得如下代数方程组 6A1A2+2A1=0, 6b3A1A2+2b3A1=0, 18bA1A2+2bA1+ωA1+6A0A1=0, 18b2A1A2+2b2A1+b ωA1+6bA0A1=0, 解此代数方程组得到如下解 (17) (18) 将(16)~(18)式以及ξ=x+ωt代入到(14)式就得到KdV方程的如下解 值得指出的是也可以用其他的辅助方程来替代G′/G-展开法中函数G所满足的辅助方程(1)来寻找非线性方程的解,可能出现所选择的辅助方程对某些非线性方程是适用的,对另一些非线性方程不适用的情况. [1]FANEn-gui.Extendedtanh-functionmethodanditsapplicationstononlinearequations[J].Phys LettA,2000,277:212. [2]ZHANG Jin-liang,REN Dong-feng,WANG Ming-liang,et al.The periodic wave solutions for the generalized Nizhnik-Novikov-Veselov equation[J].ChinPhys,2003,12(8):825. [3]WANG M L,LI X Z,ZHANG J L.The(G′/G)-expansion method and traveling wave solutions of nonlinear evolution equations in mathematical physics[J].PhysLettA,2008,372:417. [4]SIRENDAOREJI,SUN Jiong.Auxiliary equation method for solving nonlinear partial differential equations[J].PhysLettA,2003,309(5-6):387 [5]ZHANG Sheng,XIA Tie-cheng.A generalized auxiliary equation method and its application to(2+1)-dimensional symmetric Nizhnik-Novikov-Vesselov equations[J].JPhysA:MathTheor,2007,40:227. [6]MAHA S M SHEHATA.The exp(-φ(ξ)) method and its applications for solving some nonlinear evolution equations in mathematical physics[J].AmJComputMath,2015,5:468. (责任编辑孙对兄) A generalization of theG′/G-expansion method and its applications Sirendaoerji (College of Mathematical Science,Inner Mongolia Normal University,Huhhot 010022,Inner Mongolia,China) A new method to construct the exact traveling wave solutions of nonlinear equations is proposed by using the elliptic equation and the Riccati equation in place of the auxiliary equation which satisfied by the function in theG′/G-expansion method.Our method is examined by taking the KdV equation as an illustrative example.The proposed method also can be applied to solve other nonlinear equations. G′/G-expansion method;elliptic equation;Riccati equation 10.16783/j.cnki.nwnuz.2016.05.006 2016-03-20;修改稿收到日期:2016-07-08 国家自然科学基金资助项目(11261037,11361040);内蒙古自然科学基金项目(2014MS0111);内蒙古师范大学“十百千”人才培养工程项目(RCPY-2-2012-K-033) 斯仁道尔吉(1954—),男,内蒙古正蓝旗人,教授,博士.主要研究方向为孤立子与可积系统理论. E-mail:siren@imnu.edu.cn O 175.29 A 1001-988Ⅹ(2016)05-0024-03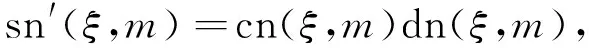

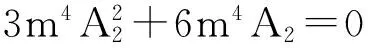
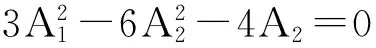
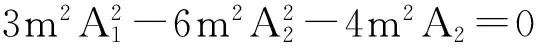
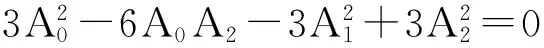
2 双曲函数与三角函数解