参数型Marcinkiewicz交换子在非齐性度量测度Hardy 空间上的估计

陶双平，王杰为

(西北师范大学数学与统计学院，甘肃兰州　730070)



参数型Marcinkiewicz交换子在非齐性度量测度Hardy 空间上的估计

陶双平，王杰为

(西北师范大学数学与统计学院，甘肃兰州730070)

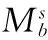
非齐度量测度空间；参数型 Marcinkiewicz 积分； Hardy空间；交换子；有界算子

1　引言及主要结果

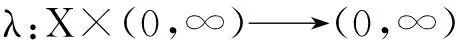
(1)

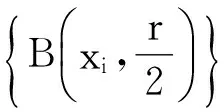
设函数K(x,y)是定义在(X×X){(x,x):x∈X}上的局部可积函数，满足：

( i )存在一个常数C>0，使得对任意的x,y∈X,x≠y，有

(2)

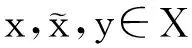
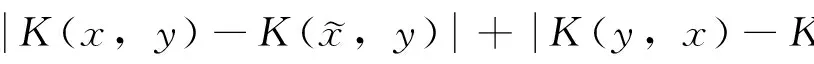
(3)

参数型Marcinkiewicz积分算子定义为

(4)

则(4)式定义的积分算子Ms就是经典的参数型Marcinkiewicz积分[11]，并且当s=1时，M1恰为Stein于1958年首次定义的n维Marcinkiewicz积分算子[12].

(5)

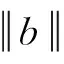
设函数b∈Lipβ(μ),相应的参数型Marcinkiewicz积分交换子

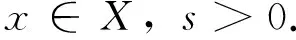
(6)

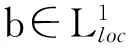
(i)存在球B，使得supp(b)⊂B;

(ii)∫Xb(x)dμ(x)=0;

(iii)存在函数aj，supp(aj)⊂Bj⊂B及常数kj∈C，使得b=k1a1+k2a2,j=1,2，且

那么称b为一个(p,1)λ原子块,记

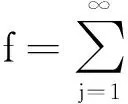
本文的主要结果如下:

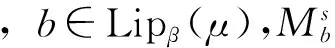
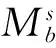
(7)

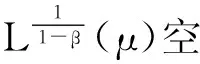
推论1在定理1的条件下,假定Ms在L2(μ)上有界，那么对任意具有紧支集的有界函数f，存在常数C>0，使得

(8)

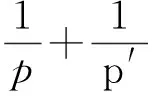
2　主要结果的证明

证明定理1,2之前,需要下面的引理.设(X,d,μ)是非齐度量测度空间，对X中的球B⊂S,记

δ(B,S)具有下面性质：

引理1[4](a)对于X中的所有球B⊂R⊂S,有δ(B,R)≤δ(B,S);

(b)对任意的ρ∈[1,∞),存在一个正常数Cρ，使得对所有球B⊂S,当rS≤ρrB时，有δ(B,S)≤Cρ;

(c)存在一个正常数C，使得对所有球B⊂R⊂S，有δ(B,S)≤δ(B,R)+Cδ(R,S).特别地，如果球B与R同心,那么C=1.

定理1的证明设函数b∈Lipβ(μ)，则由Minkowski不等式和(2)式，可得

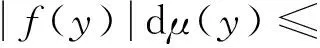
其中，Iβ为分数次积分算子，其定义为[14]

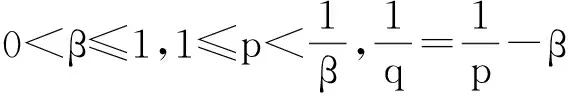
因此，定理1得证.】

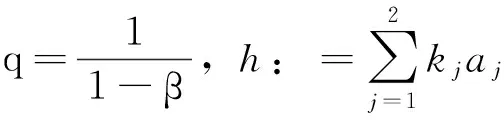
记rB为B的半径，xB为B的球心，则有

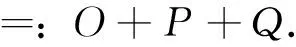
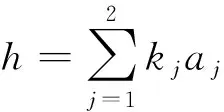
下面分别对O1,O2进行估计.首先估计O1,易见

接下来估计O11，选取p1,q1,使得

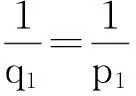
现在估计O12，记N2B1,2B为第一个使得2kB1⊃2B的正整数k，简记为N，结合Minkowski不等式及(1)和(2)式，得

其中

故

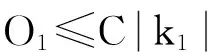
注意到，对y∈B,x∈X2B,有

所以由(2)式及Minkowski不等式，有

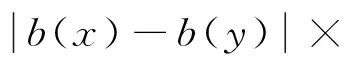
最后估计Q.对y∈B，有

结合(2)，(3)式,积分∫Bh(x)dμ(x)=0以及Minkowski不等式，有

综上所证，可得

[1]HYTÖNEN T.A framework for non-homogeneous analysis on metric spaces，and the RBMO space of Tolsa[J].PublMat，2010，54(4)：485.

[2]COIFMAN R.R,WEISS G.AnalyseHarmoniqueNon-commutativesurCertainsEspacesHomogènes[M].Lecture Notes in Math.242，Berlin:Springer，1971.

[3]TOLSA X.BMO,H1and Calderón-Zygmund operators for non-doubling measures[J].MathAnn，2001，319：89.

[4]YANG D，ZHOU Y.Boundedness of Marcinkiewicz integrals and their commutators inH1(Rn×Rn)[J].Sci China(SerA)，2006，49：770.

[5]HU G，LIN H，YANG D.Marcinkiewicz integrals with non-doubling measures[J].IntegralEquationsOperatorTheory，2007，58：205.

[6]周疆，逯光辉.具有非倍测度的参数型Marcinkiewicz积分交换子在Hardy空间中的有界性[J].高校应用数学学报，2014，29(3)：361.

[7]李亮，周疆.非倍测度下Marcinkiewicz积分交换子在Hardy空间中的有界性[J].高校应用数学学报，2013，28(2)：145.

[8]陶双平，李省哲.粗糙核Marcinkiewicz积分在Companato空间上的有界性[J].西北师范大学学报(自然科学版)，2009，45(4)：11.

[9]LIN H，Yang D.Equivalent boundedness of Marcinkiewicz integrals on non-homogeneous metric measure spaces[J].ScienceChina:Mathematics，2014，57(1)：123.

[10]陶双平,王萍.非齐度量测度空间上Marcinkiewicz交换子的Lipschitz估计[J].兰州大学学报(自然科学版),2015.

[11]HÖRMANDER L.Estimates for translation invariant operators inLpspaces[J].ActaMath,1960,104:93.

[12]STEIN E M.On the functions of Littlewood-Paley,Lusin,and Marcinkiewicz[J].TransAmerMathSoc,1958,88(2):430.

[13]HYTÖNEN T，YANG Da-chun，YANG Do.The Hardy spaceH1on non-homogeneous metric spaces[J].MathProcCambridgePhilosSoc，2012，153：9.

[14]WANG D,Zhou J.Lipschitz spaces and fractional integral operators associated with nonhomogeneous metric measure spaces[J].AbstractandAppliedAnalysis，2014，Article ID 174010，8 pages.

(责任编辑马宇鸿)

Estimates for commutators of parameter Marcinkiewicz integrals on non-homogeneous metric measure Hardy spaces

TAO Shuang-ping,WANG Jie-wei

(College of Mathematics and Statistics,Northwest Normal University,Lanzhou 730070,Gansu,China)

non-honogeneousmetricmeasurespace;parameterMarcinkiewiczintegral;Hardyspace;commutator;boundedoperator

10.16783/j.cnki.nwnuz.2016.05.002

2016-01-17;修改稿收到日期:2016-04-08

国家自然科学基金资助项目(11561062)

陶双平(1964—)，男，甘肃天水人，教授，博士研究生导师.主要研究方向为调和分析.

E-mail:taosp@nwnu.edu.cn

O 174.2

A

1001-988Ⅹ(2016)05-0005-05