含有变时滞的非自治BAM神经网络周期解的全局指数稳定性
2016-10-12王继禹贾秀玲佘连兵
王继禹,贾秀玲,佘连兵
(1.河南理工大学万方科技学院,公共基础部,河南郑州 451400;2.六盘水师范学院数学系,贵州六盘水 553004)
含有变时滞的非自治BAM神经网络周期解的全局指数稳定性
王继禹1,贾秀玲1,佘连兵2
(1.河南理工大学万方科技学院,公共基础部,河南郑州451400;2.六盘水师范学院数学系,贵州六盘水553004)
利用M矩阵理论以及Halanay不等式技巧,给出了一类含有变时滞的非自治BAM神经网络周期解的全局指数稳定的充分条件,这些条件去掉了对激活函数的有界性、单调性和可微性的要求.
BAM神经网络;周期解;M矩阵;全局指数稳定性
0 引言
双向联想记忆神经网络(BAM)模型自从1988年被Kosko[1]提出以来,已在模式识别、智能处理、优化计算以及复杂控制等领域得到广泛应用.双向联想记忆神经网络已经引起了众多研究者的关注[2-7],但在现实应用中,人们发现时滞往往不可避免地出现在神经网络中,从而引起许多振荡和不稳定现象.文献[7]对时滞的杂交双向联想记忆神经网络(BAM)周期解的稳定性进行了研究,给出了一些新的结果.受文献[2-7]的启发,本文研究如下神经网络模型:
(1)
其中i=1,2,…,n;j=1,2,…,m.这里xi(t),yj(t)分别表示第i和第j个神经元在t时刻神经细胞的状态;ai(t)>0,bj(t)>0,cij(t),dji(t),pij(t),qji(t)表示t时刻的联接权值;fj,gi为激活函数;τij(t),σji(t)是以ω为周期的信号传输时滞;Ii(t),Jj(t)分别是t时刻的外部输入.
系统(1)的初始条件为
这里φi(t),ψj(t)是定义在[-σ,0]和[-τ,0]上的实值连续函数.
1 预备知识
本文假设激活函数、信号传输时滞函数和联接权值函数满足如下条件:
(H1)存在正常数Li,Mj,使对任意的x,y∈R.
(H2)0≤τij(t)≤τ,0≤σji(t)≤σ.
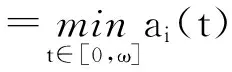
为方便起见,记
定义1若存在常数κ≥1和ε>0满足
则称系统(1)是指数稳定的,其中
这里r>1,r∈R.记
则(x*(t),y*(t))T是系统(1)的一个ω周期解.
定义2设实矩阵S=(sij)n×n的非主对角线元非正,且逆矩阵为非负矩阵,即当i≠j时,sij≤0且S-1≥0,则称S为M矩阵.
引理1[7]若a>0,b>0,p>0,q>0,p+q=1,则apbq≤pa+qb.
引理2[7]设Z(t)满足不等式:
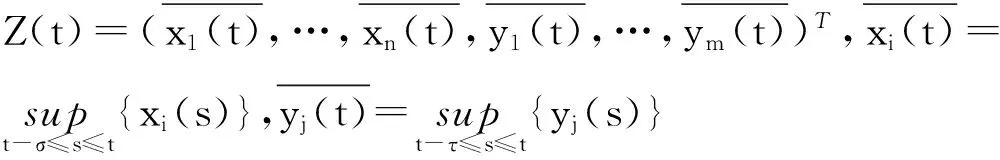
2 周期解的全局指数稳定性
定理1若(H1)~(H3)成立,且存在实数αij,α*ij,βij,β*ij,ηji,η*ji,δji,δ*ji和正整数r>1,使得

为M矩阵,则模型(1)的周期解全局指数稳定.在矩阵Σ中,
证明模型(1)可改写为:
若令
其中r为正整数,则由(H1)~(H3)和引理1可知
同理可得
令
设
则
由条件可知
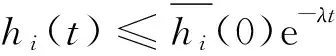
也即
同理
所以
于是由定义1可知,模型(1)的周期解全局指数稳定.】
3 例子
考虑下列带有时变时滞的BAM神经网络周期解的全局指数稳定性:
(2)
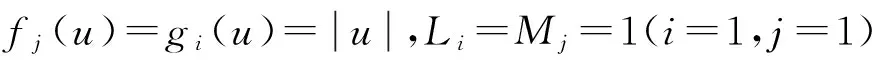
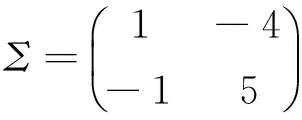
是M矩阵,因此模型(2)的周期解全局指数稳定.
[1]KOSKO B.Bi-dierctional associative memories[J].IEEETransanctionSystemManCybernet,1988,18(1):49.
[2]CAO J D,MENG D F.Exponential stability of delayed bidirectional associative memory neural networks[J].AppliedMathematicsandComputation,2003,135:102.
[3]CAO J D.Global asymptotic stability of delayed bi-directional associative memory neural networks[J].AppliedMathematicsandComputation,2003,142:333.
[4]CAO J D,LIANG J J.Global asytmptotic stability of bi-directional associative memory neural networks with distributed delays[J].AppliedMathematicsandComputation,2004,152:415.
[5]LI Y T,YANG C B.Global exponential stability analysis on impulisive BAM neural networks with distributed delays[J].JournalofMathematicalAnalysisandApplications,2006,324:1125.
[6]庞丽艳.时标上带有多变时滞的BAM神经网络的反周期解的存在性和指数稳定性[J].西北师范大学学报(自然科学版),2014,50(5):15.
[7]LI Y T,WANG J Y.An analysis on global exponential stability and the existence of periodic solutions for non-autonomous hybrid BAM neural networks with distributed delays and impulses[J].ComputersandMathematicswithApplications,2008,56:2256.
(责任编辑马宇鸿)
An analysis on global exponential stability of periodic solutions for non-autonomous BAM neural networks with time-varying delays
WANG Ji-yu1,JIA Xiu-ling1,SHE Lian-bing2
(1.Department of Public Basic Education,Wanfang College of Science and Technology,Henan Polytechnic University, Zhengzhou 451400,Henna,China; 2.Department of Mathematics,Liupanshui Normal University,Liupanshui 553004,Guizhou,China)
Applying theM-matrix theory,Halanay inequality technique and some analysis techniques,some sufficient conditions are obtained for the global exponential stability of periodic solutions for non-autonomous BAM neural networks with time-varying delays.The results remove the assumptions of the boundedness,monotonicity or differentiability of the activation functions,and in some cases,the stability criteria can be easily checked.
BAM neural network;periodic solution;M-matrix;global exponential stability
10.16783/j.cnki.nwnuz.2016.05.003
2015-09-04;修改稿收到日期:2015-12-03
国家自然科学基金资助项目(11361074);河南省教育厅重点科研项目(15A110027);河南省基础与前沿技术项目(142300410384)
王继禹(1981—),男,河南南阳人,讲师,硕士.主要研究方向为泛函微分方程定性理论.
E-mail:jywang1981@163.com
O 175.1
A
1001-988Ⅹ(2016)05-0010-04
