基于CFD的船舶顶浪遭遇畸形波数值模拟

石博文， 刘正江， 张本辉

(1.大连海事大学 航海学院， 辽宁 大连 116026; 2.海军大连舰艇学院 航海系， 辽宁 大连 116018)

基于CFD的船舶顶浪遭遇畸形波数值模拟

石博文1， 刘正江1， 张本辉2

(1.大连海事大学 航海学院， 辽宁 大连 116026; 2.海军大连舰艇学院 航海系， 辽宁 大连 116018)

针对畸形波对船舶航行极具威胁，已引发多起海上事故的情况，对舰船遭遇畸形波进行数值模拟研究。采用考虑航速改进的相位调制方法，以DTMB5512船模为目标船，在顶浪航行状态下实现舰船定时、定点遭遇畸形波的数值模拟。研究证实畸形波对舰船的不利影响明显大于一般大风浪航行，在畸形波情况下获取的非线性运动响应(包括纵摇、垂荡、垂荡加速度、压强和瞬时增阻)最大值是一般大风浪情况下的1.5倍以上。

船舶;计算流体动力学(CFD);畸形波;顶浪;数值模拟

Abstract: The freak wave is a menace to navigation, and has caused quite a few accidents. The numerical simulation of ship encountering with freak waves by means of CFD is of practical value. The phase modulation with navigation speed is proposed to improve conventional simulation method. The DTMB5512 ship model is chosen as the object of the numerical simulation. The simulation result indicates that the negative effects produced by freak waves are rather significant. The maximum value of nonlinear sea-keeping responses (including pitch, heave, acceleration of heave, pressure and instantaneous added resistance) are 1.5 times severer than those in normal rough sea environment.

Keywords: ship; CFD; freak wave; head sea; numerical simulation

畸形波是海洋中高且陡的大波，持续时间很短,但出现的偶然性和巨大的破坏性对船舶航行和海洋工程结构物等极具威胁，已引发多起海上事故。[1]因此,畸形波越来越受到人们的关注，其发生机理及工程应用问题已成为当前物理海洋学界、船舶水动力学界和航海界的研究热点[2-4]。

目前国内外学者已对畸形波的数值模拟、演化规律及其对近岸结构物的响应进行大量研究，但对舰船遭遇畸形波的摇荡运动及其动力响应的研究还相对较少。CLAUSS等[5]和BENNETT等[6]对舰船遭遇畸形波进行研究；张本辉[7]采用考虑航速、航向的改进的相位调制方法对舰船遭遇畸形波的海浪环境进行数值建模，实现船模顶浪态势下定时、定点遭遇畸形波的数值模拟，与水池试验结果吻合较好，验证了所建模型的有效性。

这里以DTMB5512船模为研究对象，在顶浪条件下对船舶遭遇畸形波及在恶劣海况下遭遇一般大风浪时的摇荡运动进行数值模拟，分析遭遇畸形波时的非线性运动响应(包括纵摇、垂荡、垂荡加速度、砰击和瞬时增阻)与遭遇一般大风浪时的不同。

1 畸形波海浪环境的生成

采用计算流体动力学(Computational Fluid Dynamics,CFD)方法模拟舰船在波浪中的运动时，假设在固定坐标系中航速为U0，则长峰不规则波的波高方程为

(1)

设在位置x=xc,时刻t=tc时生成畸形波，调制初相θi,使部分(或全部)组成波在x=xc,t=tc时ηi(xc,tc)为正，则在此叠加的波高会增大。令组成波数M=M1+M2，则式(1)可表示为

(2)

令

(3)

(4)

令后M2个组成波的合成波波面η2(x,y,t)在预定位置处聚焦,出现大波，需调制后M2个组成波的初相位θi，使ηi(xc,yc,t)>0。具体调制方法见文献[7]。

2 DTMB5512船模顶浪遭遇畸形波的数值模拟

2.1数值模拟方案

选择DTMB5512船模作为研究对象，该船数据翔实，是国际船模试验水池会议(International Towing Tank Conference,ITTC)推荐的用于CFD计算的标准船模，其主要参数见表1。

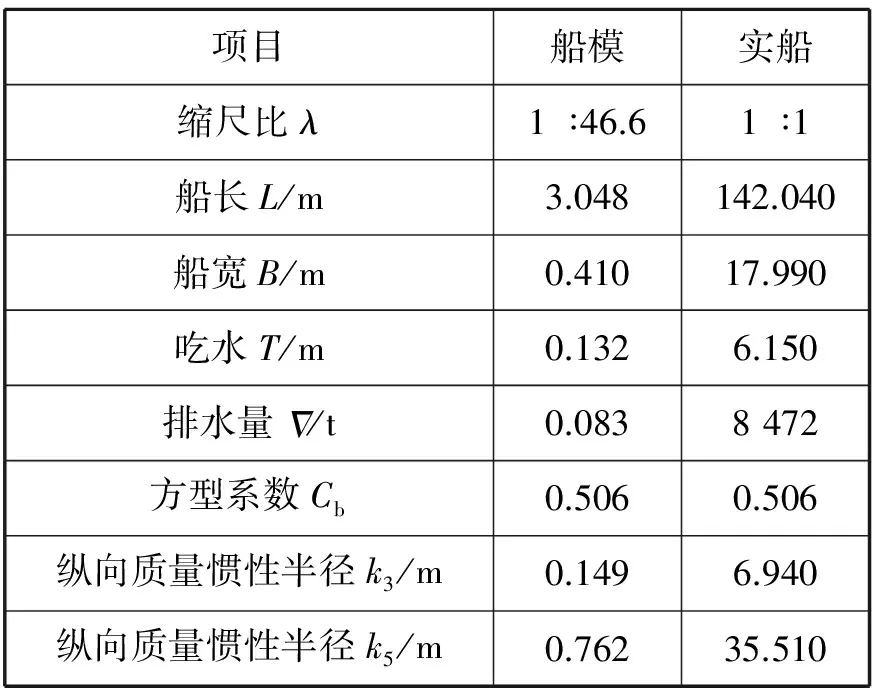
表1 DTMB5512模型主要参数

在数值水池参数相同的情况下，设计以下2种工况的试验。

1) 工况1:采用完全随机的方法，进行不断尝试，使舰船在有限的时间尺度范围内遭遇的随机波浪的最大波高(采用下跨零点法统计得到)接近H1/10，而不是文献[6]中根据瑞利分布公式获取的最大期望波高，前者更加符合海上的实际情况。

2) 工况2:采用相位调制方法，使舰船定时定点遭遇畸形波。

数值水池试验的主要参数见表2。

表2 数值水池试验的主要参数

在艏甲板和艏舷侧不同部位处设置监测点(见图1，其中:P1,P2和P3点用于监测砰击压强;P4点用于监测上浪压强)，以比较2种工况下艏部不同部位处冲击载荷强度和上浪的差异。

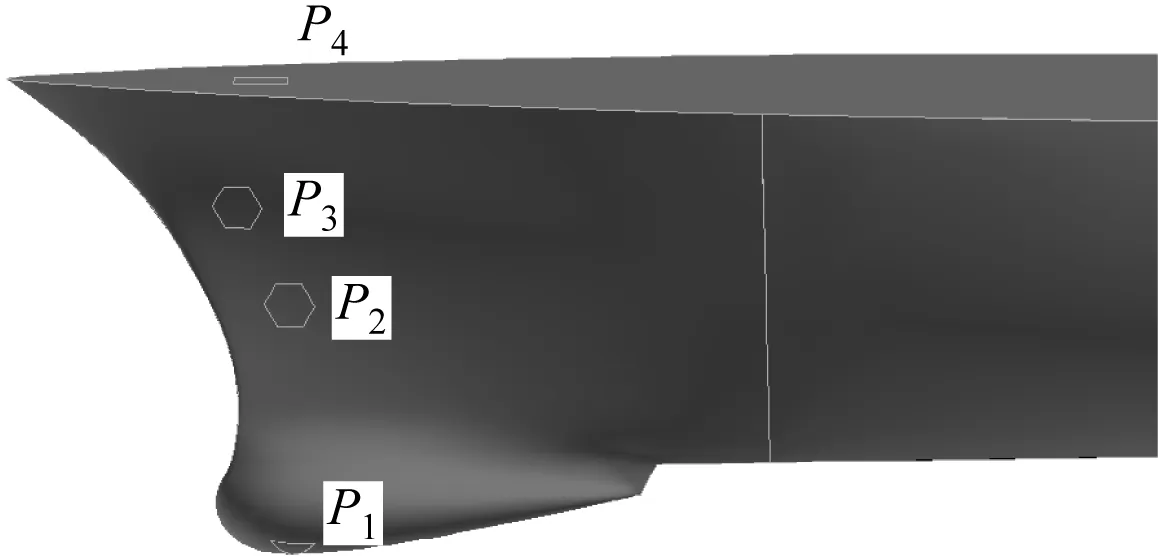
图1 上浪、砰击压强监测点位置

2.2计算域、网格划分及边界条件

计算域设置为长方体，尺寸为：入口距艏部1L，出口距艉部2L，顶部边界距水线0.5L，底部边界距水线1.5L，左、右边界距舯纵剖面1L。计算域中各边界条件名称见图2，具体设置如下。

图2 计算域中各边界名称

1) 入口边界(in)：速度入口条件，设置入口处流体的速度、水的体积分数、湍动能k和耗散率ε。

2) 出口边界(out)：压力出口条件，设定静压力、底面位置和自由面高度，回流的湍动能k及耗散率ε则采用Fluent的推荐值。

3) 上下边界(top,bot)：速度入口，给定3个方向流速(u=U0,v=w=0)及水的体积分数。

4) 左右边界(port,stab)：滑移的壁面。

5) 船体(ship)：无滑移的壁面。

采用结构非结构混合网格划分计算域，网格共有1 911 157个。采用网格整体移动方法与滑移网格方法相结合的动网格方案，对船舶两自由度摇荡运动进行数值模拟。该方法的思路为：根据船体所受的力和力矩计算出船体的线速度及角速度，使计算域内所有网格随船体一起做垂荡和纵摇运动，这样可保持计算域内网格的空间拓扑结构不变，有效避免数值计算中因网格质量下降而导致计算发散。

2.3数值模拟结果及分析

2.3.1数值波浪环境的模拟结果

在数值水池工作区中横向距离船模中心y=2.5 m处设置浪高仪，进行波浪时历监测，2种工况下采集到的波浪时历见图3。工况1的波浪时历为一般的随机海浪，利用下跨零点法求得其最大波高为0.126 3;在随机海浪情况下，由非规则波的统计特性可知，H1/10=1.275Hs=0.127 5,两者的相对误差为0.92%，工况1中采集的波浪时历可满足试验需求。

图3 2种工况下采集的波浪时历

利用下跨零点法对工况2获取的时历所包含的极值大波进行波高特征统计，其畸形波参数见表3。由KLINTING等[8]对畸形波的定义可知，工况2采集的波浪时历满足试验需求。

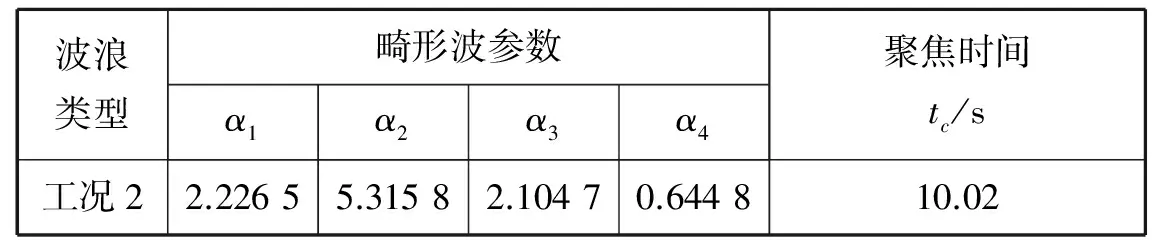
表3 工况2波浪时历的特征统计

2.3.2船模摇荡运动的模拟结果

图4为DTMB5512船模遭遇畸形波时的瞬时波面图(t=9.0～11.0 s，每隔0.5 s取一幅图片，畸形波出现时刻为10.0 s)。

从图4中可看出:船舶在包含畸形波的非规则波浪中顶浪航行时，出现明显的砰击、上浪、淹埋和球鼻艏出水等强非线性现象;而在遭遇大风浪时，船舶的摇荡起伏加剧，并没有如此明显的动力响应。

a) t=9.0 s

b) t=9.5 s

c) t=10.0 s

d) t=10.5 s

在2种工况下测得的DTMB5512船模纵摇、垂荡及垂荡加速度(与重力加速度g相除进行归一化)时历见图5。利用下跨零点法对2种工况下的纵摇θ、垂荡ξ和垂荡加速度a时历进行统计分析，求取其谷-峰最大值，结果见表4。

a) 纵摇时历

b) 垂荡时历

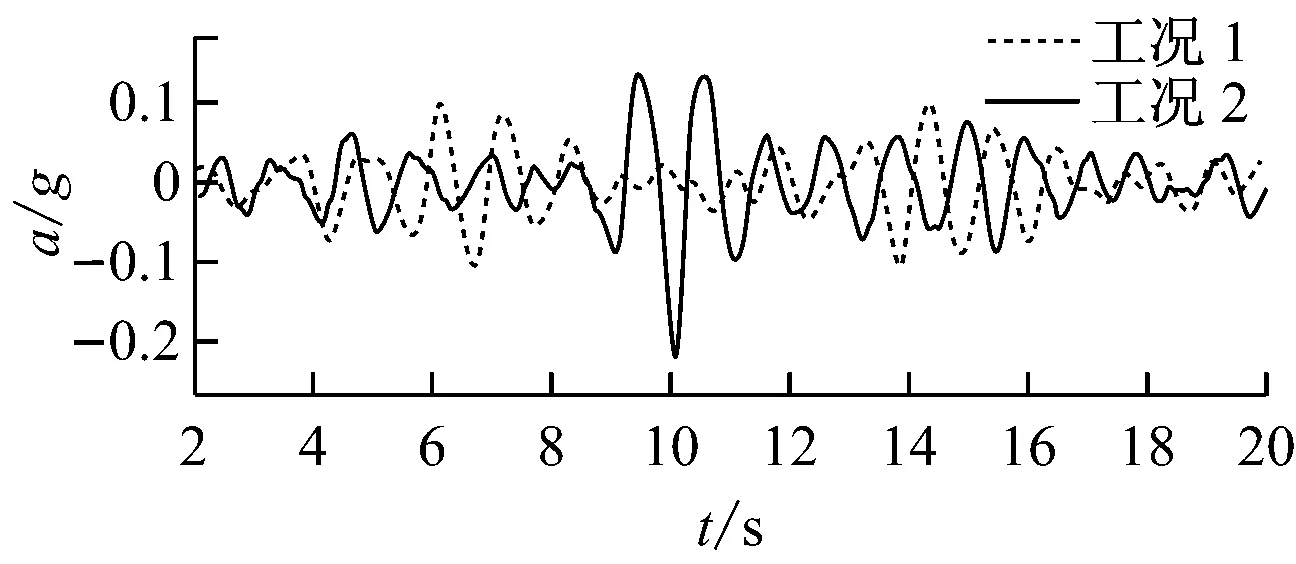
c) 垂荡加速度时历

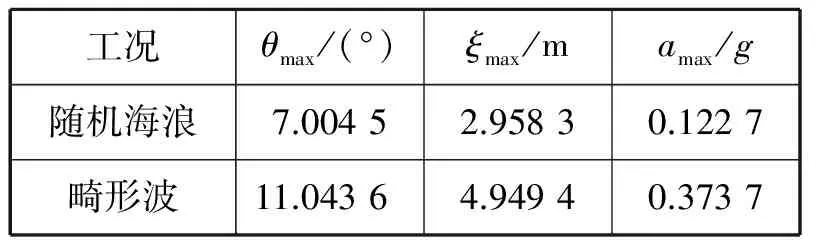
表4 2种工况下的统计数据分析

由图5和表4可知，DTMB5512船模遭遇畸形波时的最大纵摇、垂荡和垂荡加速度都明显大于遭遇一般随机海浪情况下的值。船模遭遇畸形波情况下的纵摇和垂荡分别是遭遇随机海浪情况下的1.576 6倍和1.673 1倍；而垂荡加速度的比值为3.045 6。2种工况下的垂荡加速度都小于英国劳氏船级社(Lloyd’s Register of Shipping,LR)的规范值0.39，这是在航速相对较低情况下的结果；若舰船以较高的航速顶浪遭遇畸形波，则垂荡加速度可能超越船级社的规范值。

2.3.3船体砰击的模拟结果

DTMB5512船模在遭遇随机海浪和畸形波2种工况下，压力监测点P1,P2和P3处压强值变化对比见图6。

a) P1点

b) P2点

c) P3点

分析各监测点处压强值随纵向运动值的变化趋势可知:各个监测点先后入水，压强随之迅速增大;达到峰值后，随着监测点入水深度增加，监测点的压强缓慢下降;当艏部由下沉转为上浮时，监测点的压强迅速降低;当监测点出水后，只有空气的作用，监测点的压强降低到最低。监测点P1(即艏部底端)处的冲击压强最大，其他部位的冲击压强从下到上、从前到后逐渐减小。在进行船舶设计时，应考虑到不同部位可能遭受的砰击载荷。遭遇畸形波时的压强值大于随机海浪情况，一般前者P1，P2和P3的最大值比后者的最大值大700 Pa左右。

一般认为艏部出水回落时，其底部与水波的相对速度达到一定值时的速度为临界速度。临界速度随船型和船长的不同而不同，奥奇提出砰击的临界速度[9]近似取为

(5)

艏部拍击水面时的相对速度可由船舶本身的垂向速度和水波垂向的分量2部分组成。在2种工况下，DTMB5512艏部的相对速度vR时历见图7。

图7 DTMB5512艏部的相对速度时历

由砰击的定义可知，船舶在设定的大风浪海况下顶浪航行时，由于球鼻艏处入水较深，未发现明显的砰击，仅出现4次vR较大的情况；而遭遇畸形波时，则出现2次明显的砰击。由图6可知，舰船遭遇畸形波时砰击达3 800 Pa左右，相当于实船底部瞬时压强超过了17.67 t/m2，是比较严重的，应充分计入风险评估中，并考虑应对举措。

2.3.4船体上浪的模拟结果

DTMB5512船模在遭遇随机海浪和畸形波2种工况下，上浪压力监测点P4处压强值变化对比见图8。通过分析P4处的压强值随纵向运动值的变化趋势可知：在随机海浪情况下没有上浪产生，因此P4值接近于0；而在舰船遭遇畸形波时则产生明显的上浪，且压强值相对较大，差异比较明显，差值接近于2 000 Pa；同时，出现了2个峰值，说明出现2次明显的上浪。

图8 2种工况下P4监测点处压强值变化对比

2.3.5增阻的模拟结果

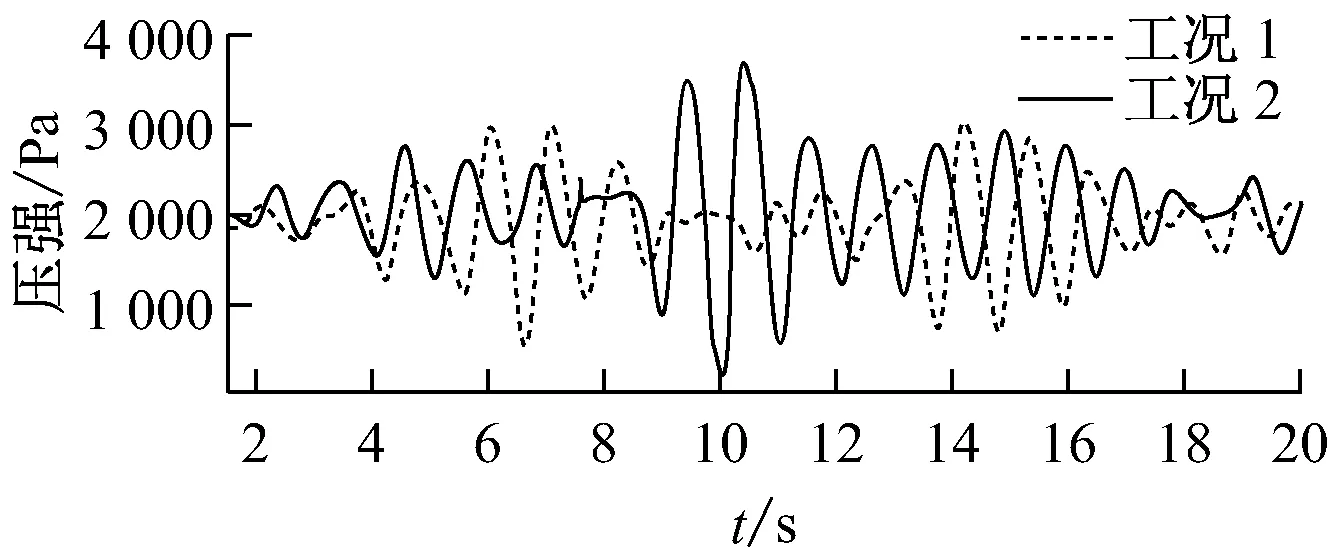
在顶浪态势下，舰船在2种工况下的阻力变化曲线见图9。在2种工况下最大瞬时阻力和最大瞬时增阻对比见表5。

图9 船模在2种工况下的阻力变化曲线

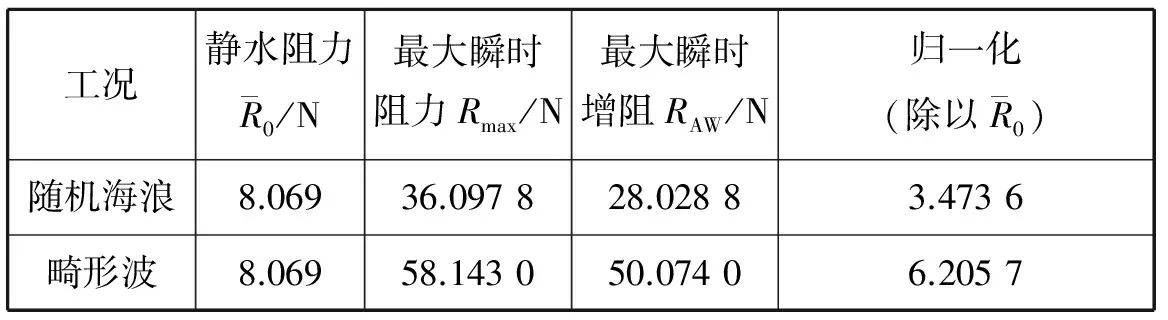
表5 在2种工况下最大瞬时阻力和最大瞬时增阻对比

由表5可知，畸形波海况下增阻归一化之后的值约为遭遇一般大风浪情况下归一化值的2倍。舰船在恶劣海况下的瞬时阻力有可能使螺旋桨突然超负荷工作，将会对舰船的动力产生巨大的影响。

3 结束语

以DTMB5512船模为目标船，对现代中型舰船顶浪、遭遇畸形波的非线性摇荡运动和动力响应进行数值模拟研究，得到以下结论：

1) 在顶浪情况下对舰船在同一海况下遭遇大浪和畸形波进行数值模拟的比较研究，包括纵摇、垂荡、垂荡加速度、砰击、上浪和瞬时增阻等诸多方面，给出比较精确的量化结果。

2) 就舰船在同一海况下以常速(12 kn)顶浪航行而言，遭遇一般大风浪和遭遇畸形波，其航行风险有很大差异。在遭遇畸形波的情况下，即使是8 000吨级以上的现代化舰船，也需考虑减速、调整航向(甚至是规避)等举措，以减少损失。

[1] 董艳秋,纪凯,黄衍顺.波浪中船舶横摇稳性的研究[J].船舶力学,1999,3(2):1-6.

[2] 刘首华,牟林,刘克修,等.畸形波研究的进展及存在问题[J].地球科学进展,2013, 28(6):665-673.

[3] 高志一,于福江,徐福祥,等.畸形波生成条件预报方法研究进展[J].海洋通报,2011,30(3):351-356.

[4] 沈玉稿. 畸形波的数值模拟及其与海洋结构物相互作用研究[D].上海:上海交通大学,2013.

[5] CLAUSS G F,KLEIN M,KAUFFELDT A. Limiting Loads and Motions of Ships in Extreme Sea States[C]//13th Congress of Int1.Maritime Assoc.Istanbul,2009:12-15.

[6] BENNETT S S,HUDSON D A,TEMAREL P. The Influence of Forward Speed on Ship Motions in Abnormal Waves: Experimental Measurements and Numerical Predictions[J].Journal of Fluids and Structures,2013,39(5):154-172.

[7] 张本辉.畸形波及舰船遭遇畸形波的数值模拟研究[D].大连:海军大连舰艇学院,2016.

[8] KLINTING P,SAND S.Analysis of Prototype Freak Waves[C].Coastal Hydrodynamic,1987:618-632.

[9] 吴明.不规则波中舰船摇荡运动的数值模拟及预报研究[D].大连:海军大连舰艇学院,2013.

CFDNumericalSimulationofShipEncounteringFreakWavesinHeadSea

SHIBowen1,LIUZhengjiang1,ZHANGBenhui2

(1. Navigation College, Dalian Maritime University, Dalian 116026, China; 2. Department of Navigation, Dalian Naval Academy, Dalian 116018, China)

U661.3

A

2016-05-31

总装预研基金(51314030101)

石博文(1985—),男,吉林长春人,博士生，研究方向为交通运输安全保障与防护技术。E-mail:agshi56@sina.com

1000-4653(2016)03-0059-04