大型船舶的非线性Norrbin数学模型改进

张显库, 杨光平

(大连海事大学 航海学院， 辽宁 大连 116026)

大型船舶的非线性Norrbin数学模型改进

张显库, 杨光平

(大连海事大学 航海学院， 辽宁 大连 116026)

为解决大型船舶非线性Norrbin数学模型精度不高的问题，将其与船舶大型化有关的4个流体动力导数适当放大;将Norrbin给出的2个非线性力(矩)经验公式在增加物理意义的基础上也适当放大。以40万吨级大型矿砂船“Vale Brasil”为例，将改进的Norrbin模型、原Norrbin模型和MMG(Manoeuvring Mathematical Model Group)模型与2组实船试验数据进行比较。结果表明，改进模型与实船数据的符合度最好，精度比MMG模型提高5.5%，比原Norrbin模型提高约14%，保留了原模型的参数少且物理意义明显的优点。

船舶工程; 大型船舶； 非线性Norrbin模型； 改进

Abstract: In order to improve the precision of conventional Norrbin mathematical model for large ships , the four hydromechanical derivatives reflecting the ship size increasing are magnified and the two nonlinear empirical force (moment) formulas given by Norrbin are also properly revised through expanding its physical foundation. The 400 000 t large bulk cargo ship “Vale Brasil”, as a practical case, are simulated with the improved Norrbin model, the original Norrbin model, and Manoeuvring Mathematical Model Group (MMG) model respectively, and the simulation results are compared with two sets of actual ship test data. The results show that the improved Norrbin model is the best in terms of the data coincidence. The precision of the proposed model is 5.5% higher than that of the MMG model and about 14% higher than that of the original Norrbin model, while keeping the advantages of small number of parameters and clear physical meaning.

Keywords: ship engineering; large ship; nonlinear Norrbin model; improvement

在船舶运动控制领域，Norrbin非线性数学模型因形式简洁且求取时所需船舶参数不多而备受相关研究人员[1-3]关注,但是1977年NORRBIN等[4]给出的非线性项经验公式和1983年CLARKE等[5]给出的线性数学模型流体动力导数都已使用多年，随着船舶日益朝大型化、快速化、专业化和现代化方向发展，其数学模型的精度对大型船舶来说越来越低，亟需改进。文献[6]和文献[7]均使用MMG(Manoeuvring Mathematical Model Group)模型为40万吨级大型散货船建立数学模型,进行操纵性预报和拖船协助下的大型集装箱船港内航行操纵性研究，所建立的模型具有较高的精度，但模型参数较多，使用较麻烦。这里立足于原有的经验公式，找出其中与船舶大型化有关的参数，通过开发的仿真平台，结合理论分析，对其中一些参数进行放大或缩小，使改进的模型更适用于大型船舶的操纵性预报和控制器设计等研究，提高模型的精度。以40万吨级矿砂船“Vale Brasil”为例，通过与2组实船试验数据进行比较，发现改进的Norrbin模型具有比原Norrbin模型、MMG模型更高的精度，保留了原模型参数少且物理意义明显的优点。

1 改进的Norrbin模型

Norrbin在研究船舶参数辨识问题时提出一种关于非线性流体动力fY(v,r)和力矩fN(v,r)的简洁表达式，见式(1)和式(2)。

(1)

(2)

数学模型中风、浪、流干扰的处理与原Norrbin模型相同，船舶位置计算采用文献[1]中的常规方法。

2 模型仿真试验

以40万吨级大型矿砂船“Vale Brasil”[6]为例，其参数见表1。由于文献[6]只给出压载时的2组实船回转试验数据(半速时无风回转试验和全速时有风(风速6.17 m/s，风向340°)回转试验)，因此先进行半速时无风的3组回转试验并将其与实船试验数据和文献[6]的MMG模型进行比较。这3组试验分别为：原Norrbin非线性数学模型、非线性Nomoto模型(具体模型见文献[1]，参数见表2)和改进的Norrbin非线性数学模型。用与压载半速时相同的参数进行改进后Norrbin模型的压载全速回转试验，并将其与实船试验数据和MMG模型试验进行比较，看是否仍然具有较高的精度；最后用调整好的改进Norrbin模型进行满载全速回转性能预报。

表1 “Vale Brasil”船舶参数

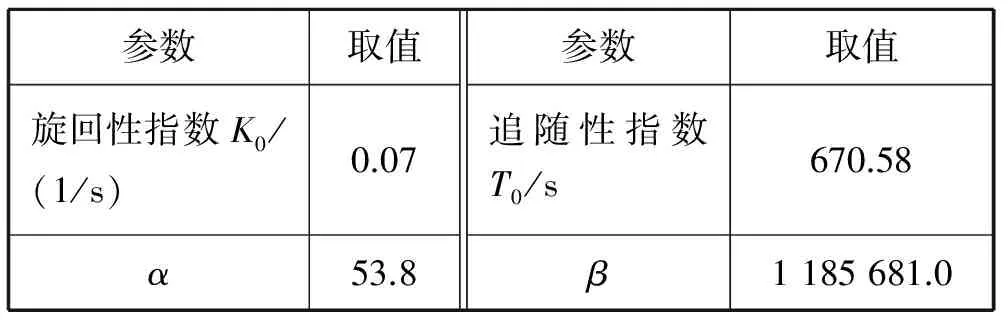
表2 基于文献[1]获得的非线性Nomoto模型参数

2.1压载半速无风试验

图1为压载半速无风时3组仿真试验与实船试验和MMG模型试验比较结果，其中横纵位置坐标均已除以船舶垂线间长，为无量纲变量。

图1 半速无风回转试验比较结果

1) 从回转半径看，实船试验为507.5 m，改进的Norrbin模型为487.4 m，MMG模型为529.5 m，原非线性Norrbin模型为476.9 m，非线性Nomoto模型为424.3 m。改进的Norrbin模型精度最高，约为96%；MMG模型精度次之；非线性Nomoto模型因是简化模型而使得精度相对最差，约为84%。

2) 从图形的符合度看，MMG模型和实船试验均向左移，原非线性Norrbin模型和非线性Nomoto模型均向下移，原非线性Norrbin模型下移量约占实船回转直径的26%。由于非线性Nomoto模型的2个非线性参数α和β都是用原非线性Norrbin模型试验取得大量数据辨识得出的，因此这2个曲线的符合度一致且非线性Nomoto模型的精度略差，这是符合理论分析的。

无论是从模型精度还是从图形的符合度来看，改进的Norrbin模型的精度都是最高的。为模拟回转过程中速度下降的效果，采用指数下降法拟合速度u的下降效果，具体为：半速时u=1.9+2.16e-t/670；全速时u=1.9+6.22e-2t/670。分析这2个公式可知：该船回转一圈后速度约降为1.9 m/s，全速时初始速度为8.12 m/s，半速时初始速度为4.06 m/s；式中的670实际上是该船的追随性指数的近似值，全速时的指数速降速率为半速时的2倍。在实际使用建好的改进模型时，速降也可采用文献[8]中给出的经验公式计算。

2.2压载全速有风试验

图2为全速有风时的回转试验比较结果，主要验证改进的Norrbin模型是否对另外一组试验具有同样的精度。

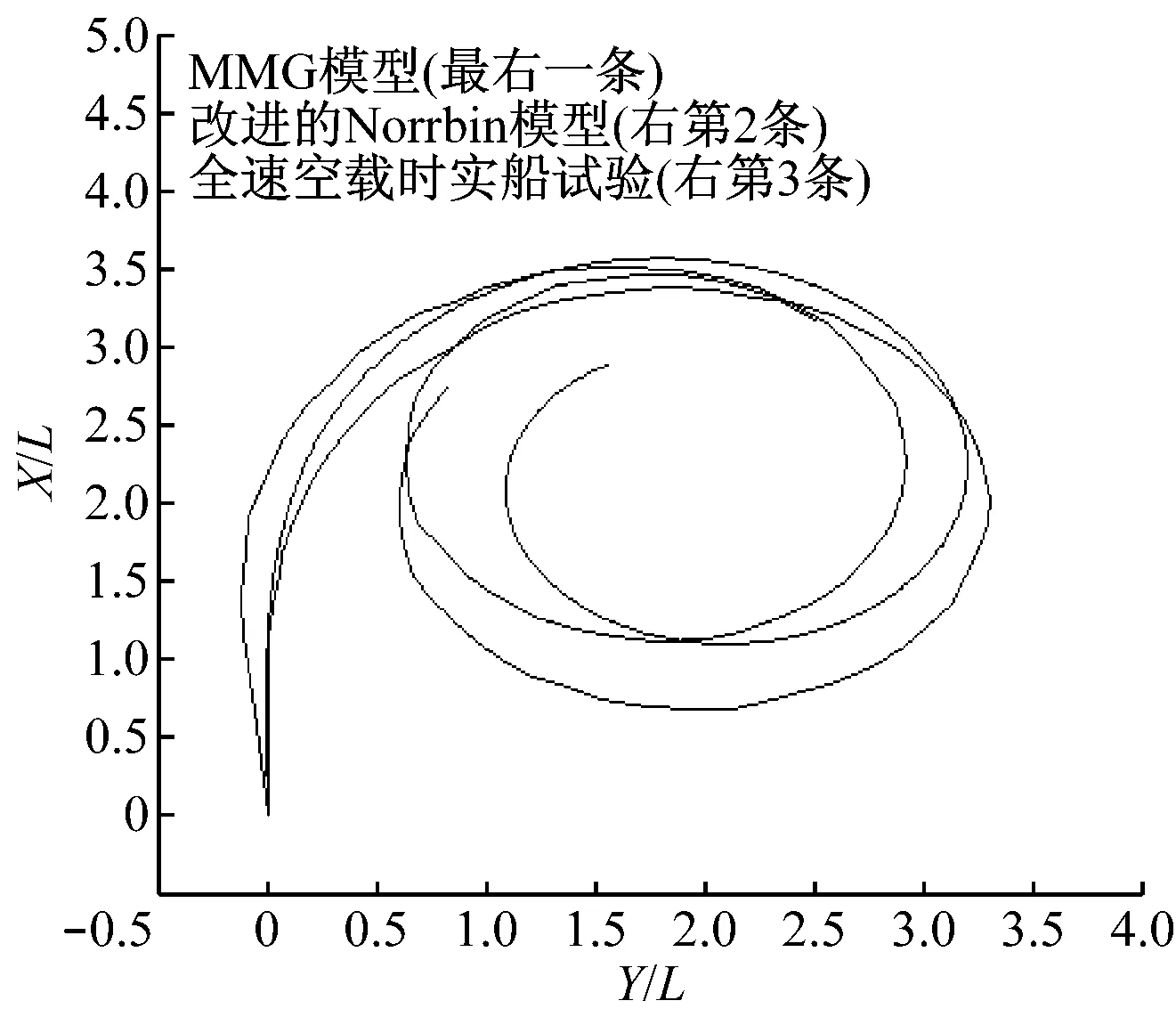
图2 全速有风时的回转试验比较结果

图2中，实船试验的回转半径为400.8 m，MMG模型的回转半径为474 m，改进的Norrbin模型的回转半径为370.2 m，其误差百分比分别为18.26%和-7.63%，显然改进的Norrbin模型精度提高了10%以上。表3为2组试验的数据比较分析，其中回转半径是通过编写的程序自动计算出来的。[9-10]

表3 2组试验的数据比较分析

综合以上2组试验数据分析可知，改进的Norrbin模型的精度比MMG模型平均提高约5.5%，模型较简单，与实船试验数据相比精度在94%左右；若考虑船舶轨迹图形符合度，则其精度比原非线性Norrbin模型提高约14%，且修改的参数少，物理意义明晰。

2.3满载全速无风试验预报

图3 全速满载无风回转试验预报结果

3 结束语

充分利用原非线性Norrbin模型的结果，根据船舶大型化特点，调整对大型船舶影响较大的4个流体动力导数，将其适当放大，把非线性项修改得更具有物理意义。对大型船舶来说,非线性项的系数也是放大的;从理论分析和试验结果看，该参数调整原理对大型船舶具有普遍性。改进的Norrbin模型的精度平均比MMG模型提高约5.5%，模型较简单；与实船试验数据相比，平均精度在94%左右；若考虑船舶轨迹图形符合度，则比原非线性Norrbin模型提高约14%，且修改的参数少，物理意义明晰。后续研究可进一步收集多艘大型船舶的数据，确定参数调整的范围及参数与船舶大型化排水体积之间的内在联系。

[1] 张显库,金一丞. 控制系统建模与数字仿真[M].2版.大连:大连海事大学出版社,2013:112-136.

[2] 张显库. 船舶运动简捷鲁棒控制[M].北京:科学出版社,2012:18-23.

[3] ZHANG Xianku, ZHANG Guoqing, ZHANG Shuhui, et al. Researches on the Williamson Turn for Very Large Carriers[J]. Naval Engineers Journal, 2013, 125(4): 113-119.

[4] NORRBIN N H. Further Studies of Parameter Identification of Linear and Nonlinear Ship Steering Dynamics[R]. Report 1920-6, SSPA, Gothenburg, Sweden, 1977.

[5] CLARKE D, GEDLING P, HINE G. Application of Manoeuvring Criteria in Hull Design Using Linear Theory[J]. Naval Architect, 1983, 11(3): 45-68.

[6] 常亮.40万吨级大型散货船操纵性研究[D].大连:大连海事大学,2012:37-40.

[7] 王化一.拖轮协助下大型集装箱船四自由度港内操纵性研究[D].大连:大连海事大学,2014:37-42.

[8] 李宗波, 张显库, 贾云. 船舶转向过程中速度下降问题的研究[J]. 航海技术, 2008,30(3):2-4.

[9] ZHANG Guoqing, ZHANG Xianku. Concise Robust Adaptive Path-Following Control of Underactuated Ships Using DSC and MLP[J]. IEEE Journal on Oceanic Engineering, 2014, 39(4):685-694.

[10] 张显库，张国庆.船舶港内掉头操纵的简捷鲁棒控制[J]. 中国航海, 2014,37(2):31-34.

ImprovementofNonlinearNorrbinMathematicalModelforLargeShips

ZHANGXianku,YANGGuangping

(Navigation College, Dalian Maritime University, Dalian 116026, China)

U661.73

A

2016-04-20

国家自然科学基金(51109020;51679024); 中央高校基本科研业务费专项资金(3132014302)

张显库(1968—)，男，辽宁辽阳人，教授,博士生导师，研究方向为船舶运动控制、鲁棒控制。E-mail: zhangxk@dlmu.edu.cn

1000-4653(2016)03-0050-04