优化的GM(1,1)幂模型在港口吞吐量预测中的应用
2016-10-12黄跃华陈海山
黄跃华, 陈海山
(1.天津海运职业学院, 天津 300350;2.温州海事局, 浙江 温州 325002)
HUANG Yuehua1, CHEN Haishan2
优化的GM(1,1)幂模型在港口吞吐量预测中的应用
黄跃华1, 陈海山2
(1.天津海运职业学院, 天津 300350;2.温州海事局, 浙江 温州 325002)
为有效预测港口吞吐量,应用优化理论,通过非线性规划的方法求解幂指数,建立优化幂指数的GM(1,1)幂模型。首次将该模型应用于港口吞吐量预测中,并以天津港港口吞吐量数据为例进行模拟和预测。结果表明:基于优化幂指数的港口吞吐量GM(1,1)幂模型不但可以解决传统幂模型建模方法与模型检验脱节的问题,而且其模拟和预测的精度均优于传统GM(1,1)幂模型。因此,可将该优化的幂模型应用于港口吞吐量预测中。
交通运输经济学;吞吐量;预测;灰色系统;GM(1,1)幂模型;指数优化
HUANGYuehua1,CHENHaishan2
Abstract: The GM (1,1) power model with exponents optimized with nonlinear programming is built and used for predicting the throughput of Tianjin port. The exponent optimized GM (1,1) power model is superior to traditional GM (1,1) power model in that the method for building the model can also test the model. In addition, it gives more accurate estimates.
Keywords: traffic transport economics; throughput; prediction; grey system; GM(1,1) power model; exponent optimization
港口吞吐量预测在确定港口发展规划方向、未来投资规模和未来经营管理策略等方面有着重要的作用。通过对港口货物吞吐量进行科学、合理的预测,港口当局不仅能依据所预测的数据作出正确的决策,而且能避免港口发展的规模大于市场需求造成的资源浪费。目前预测港口吞吐量的方法有很多,如指数平滑法[1-2]、线性回归法[3-4]、系统动力学法[5]、组合模型法[6]和灰色模型法[7-8]等,其中指数平滑法、线性回归法、系统动力学法和组合模型法的一个共同特点是需要大量的相关统计数据,而这些数据在实际工作中难以满足建模要求,同时变量选取不当也会导致预测效果不理想。
灰色理论将系统作为一个灰色系统过程,运用部分已知的信息挖掘未知信息,因而可不用研究影响港口吞吐量的内部相关因素及其相互关系,把影响吞吐量的因素作为一定范围内变化的与时间有关的灰色变量,挖掘数据自身有用的信息建立模型、揭示规律、作出预测。[9]
GM(1,1)幂模型是一种重要的非线性灰色模型,传统的GM(1,1)和灰色Verhulst模型均为幂模型的特殊形式。优化GM(1,1)幂模型的突出优点在于:与实际应用数据最匹配的幂指数的数值可通过一定的方法被找到,且模型能较好地反映实际数据的非线性特征,具有较高的模拟和预测精度。[10]王正新等[11]以平均相对误差最小化为目标,以参数之间的关系为约束条件,构建非线性优化模型,对传统GM(1,1)幂模型进行优化,并以我国高中升学率的数据为例进行验证,其模拟和预测精度均高于传统模型。这里首次将优化GM(1,1)幂模型应用于天津港口吞吐总量的预测中,实践证明,改进的预测模型的预测精度相比传统GM(1,1)模型[10]提高效果明显,对促进港口正确决策具有重大意义。
1 传统GM(1,1)幂模型
GM(1,1)幂模型的计算方法如下。
1.1模型建立
1)设港口历史吞吐量数据为
X(0)=(x(0)(1),x(0)(2),…,x(0)(n))
(1)
2)对吞吐量数据进行一阶累加,得
X(1)=(x(1)(1),x(1)(2),…,x(1)(n))
(2)
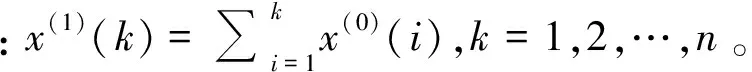
3)根据X(1)序列生成紧邻均值序列,即
Z(1)=(z(1)(1),z(1)(2),…,z(1)(n))
(3)
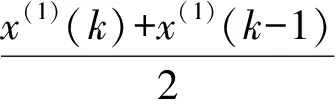
4)设x(0)(k),x(1)(k),z(1)(k)如上所述,则灰色微分方程为
x(0)(k)+az(1)(k)=b(z(1)(k))α,α≠1
(4)
该方程称为GM(1,1)幂模型。
5)GM(1,1)幂模型白化微分方程为
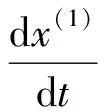
(5)
式(5)中:a,b,α为待定系数;t为时间。
1.2模型参数求解
根据式(4)对参数列(a,b)T作最小二乘估计,得
(a,b)T=(BTB)-1BTY
(6)
式(6)中:
求解式(5)便可得时间响应式为
(7)

(8)

2 GM(1,1)幂模型的幂指数优化[11]
GM(1,1)幂模型幂指数优化计算方法如下。
由式(6)可知,若幂指数α确定,则公式模型中参数a和b也就随之确定。首先展开GM(1,1)幂模型中的参数a和b的表达式,并将数据矩阵B和Y代入到式(6)中整理得
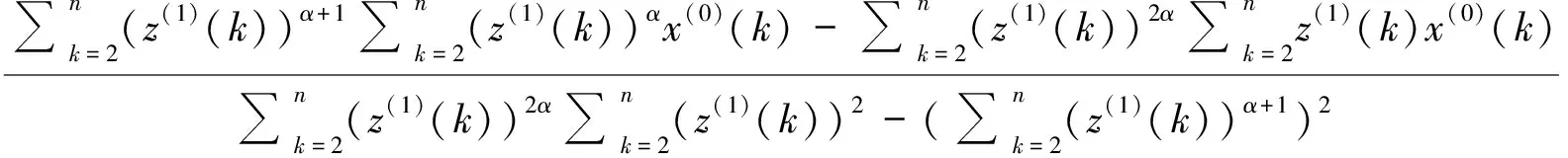
(9)
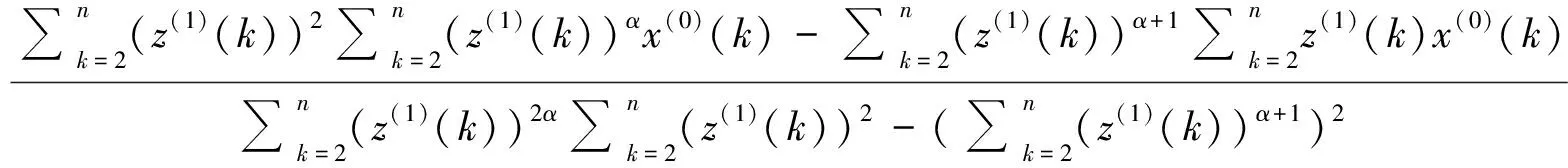
(10)
以获得的预测吞吐量平均相对误差最小化为目标,以幂指数α与参数a和b之间的关系为约束条件建立下列优化模型,求得最优的幂指数α的值,使吞吐量预测模型的平均相对误差的绝对值在理论上达到最小。
(11)
(12)
运用MATLAB和Excel等相关软件,根据式(11)和式(12)可很方便地求解式(7)中的参数α,a和b的优化值。将通过以上方式获得的参数值代入到式(7)中便可获得优化模型。
3 模型精度评估
3.1残差的相对误差检验
残差为实际吞吐量与预测吞吐量之间的差,将第k时刻的吞吐量相对误差(Throughput Relative Percentage Error)记为TRPE(k),其表达式为
(13)
将所有时刻的吞吐量平均相对误差(Throughput Average Relative Percentage Error)记为TARPE,其表达式为
(14)
1)当k≤n时,称TRPE(k)为k时刻吞吐量模拟相对误差;当k>n时,称TRPE(k)为k时刻吞吐量预测相对误差,称TARPE为吞吐量平均模拟相对误差;当TRPE和TARPE在要求的相对误差范围内时,称吞吐量模型为残差合格模型。
2)吞吐量平均模拟相对精度为1-TARPE(k);1-TRPE为k时刻吞吐量模拟相对精度。
3.2模型精度检验标准[10]
通常将误差5%设定为界定标准,即当残差的相对误差<5%时为残差合格模型,相对误差>5%时认为残差不合格。
4 模型验证评价及预测
为评价优化幂模型的模拟和预测效果,选用天津港2006—2014年的吞吐量数据(见表1)对模型进行模拟和预测效果验证,数据来自于天津市统计局网站。选取天津港2006—2012年的吞吐量数据作为建模数据,2013—2014年的数据作为验证数据。

表1 2006—2014年天津港货物吞吐量数据 万t
4.1传统幂模型求解方法[10]

4.2优化幂指数计算方法

根据式(8)、式(13)和式(14)对吞吐量预测值再作一阶累减还原计算,并预测2013—2014年的吞吐量。2种模型的模拟和预测精度比较见表2。
由表2可知,建立的吞吐量优化模型的模拟精度显著高于传统模型,优化模型完全满足TARPE<5%和TRPE<5%的要求,为残差合格吞吐量预测模型。与传统模型相比,优化模型在预测方面的优势也十分明显,同时1步预测、2步预测的相对误差均在2%之内。
4.3利用优化模型进行预测

表2 2007—2014年天津港货物吞吐量2种模型的数据比较
根据式(8)、式(13)和式(14)对吞吐量预测值再作一阶累减还原计算,并预测2015—2017年吞吐量,模型的模拟与预测精度比较见表3。

表3 2015—2017年天津港货物吞吐量预测
由表3可知,TARPE=0.66<5%且TRPE<5%,模型为残差合格吞吐量预测模型,预测2015—2017年吞吐量分别为56 840.25万t,60 064.61万t和63 401.62万t。
5 结束语
应用幂模型优化理论,通过非线性规划的方法优化幂指数,找到最佳拟合吞吐量数据的模型,为提高吞吐量数据建模精度提供一种有效的途径。结果表明,该模型与传统GM(1,1)幂模型相比可显著提高模拟和预测精度。此外,通过预测天津港2015—2017吞吐量为港口规划发展提供参考。
[1] 关克平,齐梦雅.基于指数平滑法的宁波-舟山港港口吞吐量预测研究[J]. 中国水运(下半月),2013(12):28-29.
[2] 王慧,陈浩.基于三次指数平滑法的钦州港货物吞吐量预测[J].珠江水运, 2013(Z1):169-170.
[3] 王文.线性回归结合季节性复合序列的深圳港集装箱吞吐量预测[J].中国水运(下半月),2012(12):23-25.
[4] 陈秀瑛,古浩.灰色线性回归模型在港口吞吐量预测中的应用[J]. 水运工程,2010(5):90-92.
[5] 许长新,严以新,张萍.基于系统动力学的港口吞吐量预测模型[J].水运工程, 2006(5):26-28.
[6] 赵刚,朱超,封学军.组合预测在港口吞吐量预测中的应用研究[J].水运工程,2005(3):34-36.
[7] 陈洁,许长新.改进的灰色模型在港口吞吐量预测中的应用[J]. 水运工程, 2005(1):20-23.
[8] 林强,陈一梅.灰色多元回归模型在港口吞吐量预测中的应用[J].水运工程, 2008(7):77-80.
[9] 王正新,党耀国,刘思峰,等.GM(1,1)幂模型求解方法及其解的性质[J].系统工程与电子技术, 2009, 31(10): 2380-2383.
[10] 邓聚龙.灰色预测与决策[M].武汉:华中理工大学出版社,2002:176-177.
[11] 王正新,党耀国,赵洁珏.优化的GM(1,1)幂模型及其应用[J].系统工程理论与实践,2012,32(9):1973-1976.
OptimizedGM(1,1)PowerModelforPredictingPortThroughput
(1. Tianjin Maritime College, Tianjin 300350, China;2. Wenzhou MSA, Wenzhou 325002, China)
U691.71
A
2016-01-30
黄跃华(1980—),男,天津人,讲师,硕士,从事舶舶交通工程研究。E-mail:11618378@qq.com
1000-4653(2016)02-0131-04
