基于谱分析的复杂网络脆弱节点发现算法

尹峻松，王晓明，张新强，王春江

(中国电子设备系统工程公司研究所，北京 100141)



基于谱分析的复杂网络脆弱节点发现算法

尹峻松，王晓明，张新强，王春江

(中国电子设备系统工程公司研究所，北京 100141)

未来以网络为中心的信息化战争，节点打击、毁点瘫面成为攻击敌方信息网络、夺取信息优势的重要手段。针对寻找敌方网络弱点进行攻击、提升我方体系抗毁能力拒止攻击等问题，在复杂网络拓扑连接矩阵的基础上，引入Laplacian谱分析方法，提出拓扑连接度概念，通过计算网络中各节点的拓扑连接度，发现脆弱节点并给出脆弱性排序，为信息网络的健壮性与抗毁性研究提供了一种有效的全新思路。

复杂网络；社团结构；Laplacian谱分析；脆弱节点

0　引言

随着军队信息化建设的推进，军队对于各类信息基础设施的依赖性也在不断提高，节点打击逐渐成为军事打击行动中最有效的攻击方式，能够以最小的代价破坏敌方的电力网、交通网、通信网、金融网和后勤保障网等网络链路的关键枢纽，使敌方指挥与行动受限，为战争的最后胜利奠定基础。相对于日常通信、运输网络，军用网络更强调在恶劣环境以及节点打击下的抗毁能力，因为军事网络面对的主要是有目的性的攻击而不是随机攻击。因此，如何选择敌方网络中的脆弱节点进行打击，以及对基础网络如何优化、重点防护，提高网络的健壮性与抗毁性，是夺取信息优势亟需解决的重要课题[1]。

复杂网络是一种典型的基于图的数据挖掘方法(Graph-based mining)，将数据对象抽象为节点，将对象间的关系抽象为边[2]。其骨干网抽取有一定研究，可以为提高网络的抗毁性提供依据，但对脆弱节点的发现因比较困难，目前研究较少。

本文基于复杂网络，引入Laplacian谱图理论，通过计算各节点的拓扑连接度并排序，提出了网络脆弱节点的发现算法，通过对空手道俱乐部网络、宽吻海豚网络、亚马逊图书销售网络进行仿真分析，实验结果表明，本算法可以直观、准确地发现复杂网络的脆弱节点。

1　基本概念

复杂网络中的每个节点扮演着一定的角色，称之为成员，成员之间具有异质性和局部影响差异性，表现为抱团特性[3]，即整个网络是由若干“群(group)”或“团(cluster)”构成，每个社团内部的节点之间连接相对紧密，而社团之间的连接相对比较稀疏，如图1所示。图中包含4个社团，分别对应不同颜色的划分区域。在社团内部，节点之间的联系非常紧密，而社团之间的联系就稀疏得多。

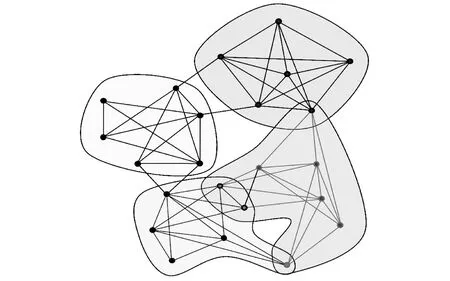
图1　一个小型的具有社团结构性质的网络示意图

在网络结构分析中，一方面需要找出网络的各个社团，根据社团划分分析出各社团的凝聚方式，这在协同推荐中非常必要，比如亚马逊和淘宝网根据不同的社团划分推荐不同兴趣的书籍和货物，使读者能够更快地检索到自己感兴趣的物品。另一方面，我们也应该注意社团和社团之间的桥接节点，或者两个社团的交叠节点[4]。这类节点离社团的中心比较远，表面上看地位不是很重要，但却是社团和社团之间连接的重要桥梁。这类节点一旦被破坏，将造成网络中不同社区的孤立，形成非连通区域甚至网络碎片。因此，对这类节点的发现，在通信网络的抗毁性分析中具有重要的意义。我们把这类节点称为脆弱节点(Fragile Node)。

2　脆弱节点发现算法

2.1Laplacian谱分析方法

设G=(V,E)是n阶简单连通图，D(G)和W(G)分别表示图G的度对角矩阵和邻接矩阵，则L(G)=D(G)-W(G)称为图G的Laplacian矩阵。

基于谱图理论，构造相应嵌入空间目标函数为：

(1)

式中，权值矩阵Wij采用Wij=exp(-‖xi-xj‖2/t)，t∈R的核函数，在满足低维结构对域的约束yTDy=1(D为对角矩阵，Dii=sumjWij)及防止网络节点收缩至单点的约束yTDI=0，最小化误差方程可对应于求解下式的最小特征向量：

Lf=λDf ，

(2)

式中，D为对角权矩阵，L=D-W即为Laplacian(对称、半正定)矩阵。

可以证明式(2)近似对应于Laplacian-Beltrami的特征向量求解[5]，因而可以反映复杂网络中各节点在该社区中的联接强度。

2.2节点拓扑连接度计算

如果一个网络由完全独立的几个社团组成，即构成他的g个社团之间不存在边，只有社团内部才存在边，那么该网络的Laplacian矩阵L就是一个分成g块的对角矩阵，其中，每一块的对角矩阵就对应着一个社团。显然，该对角矩阵有一个(最小)特征值0，对应特征值0有g个退化的特征向量，从而将网络划分为g个社区。

如果一个网络具有较明显的社团结构，但这些社团之间并不是完全独立，即构成他的g个社团并不是完全分离，而是通过少数的几条边连接，那么Laplacian矩阵就不是g块的对角阵了。此时，对应特征值0就只有一个特征向量l。但在0附近还有g-1个比0稍大一点的特征值，这些特征值对应的特征向量大致可以看作是每个社团对应特征向量的线性组合。因此，可以根据次小的g-1个特征值对应的特征向量来划分g个社区。

还有一种特殊情况，即网络中仅有2个社团，也就是说该网络的Laplacian矩阵L对应2个近似对角矩阵块。我们知道，对一个实对称矩阵来说，他的非奇异特征值对应的特征向量总是正交的。因此，除最小特征值0以外，矩阵L的其他特征值对应的特征向量总是包含正、负两种元素。这样，当网络由2个社团构成时，就可以根据非零特征值对应的特征向量中各元素对应网络的节点进行分类，其中，所有正元素对应的那些节点属于一个社团，所有负元素对应的节点属于另一个社团。

这里，次小的特征值就是该网络的代数连接度，其对应的特征向量的绝对值就称为该网络中各节点的代数连接度或拓扑连接度。

2.3基于拓扑连接度的脆弱节点发现

借鉴流形学习中Laplacian特征映射算法的思想[6]，构建基于网络拓扑的Laplacian矩阵L=D-W，D为对角矩阵，对角元素为每个节点的度，W是对称矩阵，各元素为网络所有节点之间的拓扑连接，如W(1,5)的值即为节点5对节点1的拓扑连接，有连接为1、无连接为0(简单地说，W矩阵即为网络连接矩阵)。对Laplacian矩阵计算特征值，得到节点的拓扑连接度(即次小特征值对应的特征向量的绝对值)。对拓扑连接度进行排序，势值小的节点即为该网络的脆弱节点。其核心算法流程如下：

脆弱节点发现算法流程

Step 1:构造网络拓扑Laplacian矩阵L=D-W，D为对角线元素是各节点度值的对角阵，W为网络所有节点之间的拓扑连接构成的矩阵。

Step 2:计算拓扑连接度(即矩阵L的次小特征值对应的特征向量)并排序，最小的前N项对应的节点即为脆弱节点。

本算法复杂度较低，比复杂网络分析中常用的GN算法、K-L算法要低很多(GN算法最差情况下的时间复杂度为O(m2n)，其中m、n为网络的边数和节点数)。一般情况下，计算一个n×n矩阵的全部特征向量计算复杂度为O(n3)。但在大多数情况下，实际网络的Laplacian矩阵是一个稀疏矩阵，因此，可采用Lanczos方法快速计算特征向量和特征值[7]。该方法的计算复杂度大致为m/(λ3-λ2)，其中λ3和λ2分别是第三小和第二小的特征值，而m则表示网络中边的条数。由此可见，计算速度会得到很大程度的提高。

也可以对Laplacian矩阵进行拓展，引入拓扑势的计算方法[8]，将对角矩阵D中对角元素表示为每个节点的拓扑势，将对称矩阵W的各元素表示为该节点的拓扑势值，则矩阵L中的元素就不是简单的拓扑距离，而是代表局域影响特征的拓扑势的值。计算得到的结果将更能反映节点在局部区域(社团)中的重要性。

3　实验结果分析

3.1实验网络数据描述

(1) Zachary空手道俱乐部网络

Wayne Zachary从1970～1972年观察美国一所大学空手道俱乐部成员间的社会关系，构造其成员关系网[9]，如图2所示。节点表示成员，节点间的连接表示2个成员经常一起出现在俱乐部活动之外的其他场合。因俱乐部主管John A.(节点1)与教练Mr.Hi(节点34)之间的争执而分裂成2个各自为核心的小俱乐部。网络包含34个节点，78条边。

(2) 宽吻海豚网络

D.Lusseau等人对栖息在新西兰Doubtful Sound峡湾的一个宽吻海豚群体进行长达7年的观察，构造海豚关系网[10]，如图3所示。网络中节点代表一个个海豚，边表示2个海豚之间接触频繁，网络共有62个节点159条边。

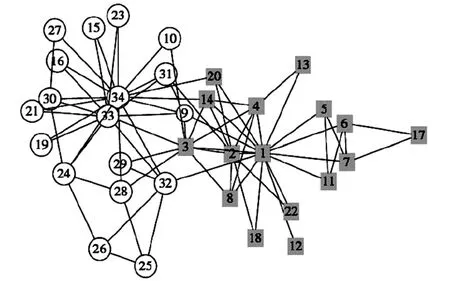
图2　Zarchy俱乐部关系图

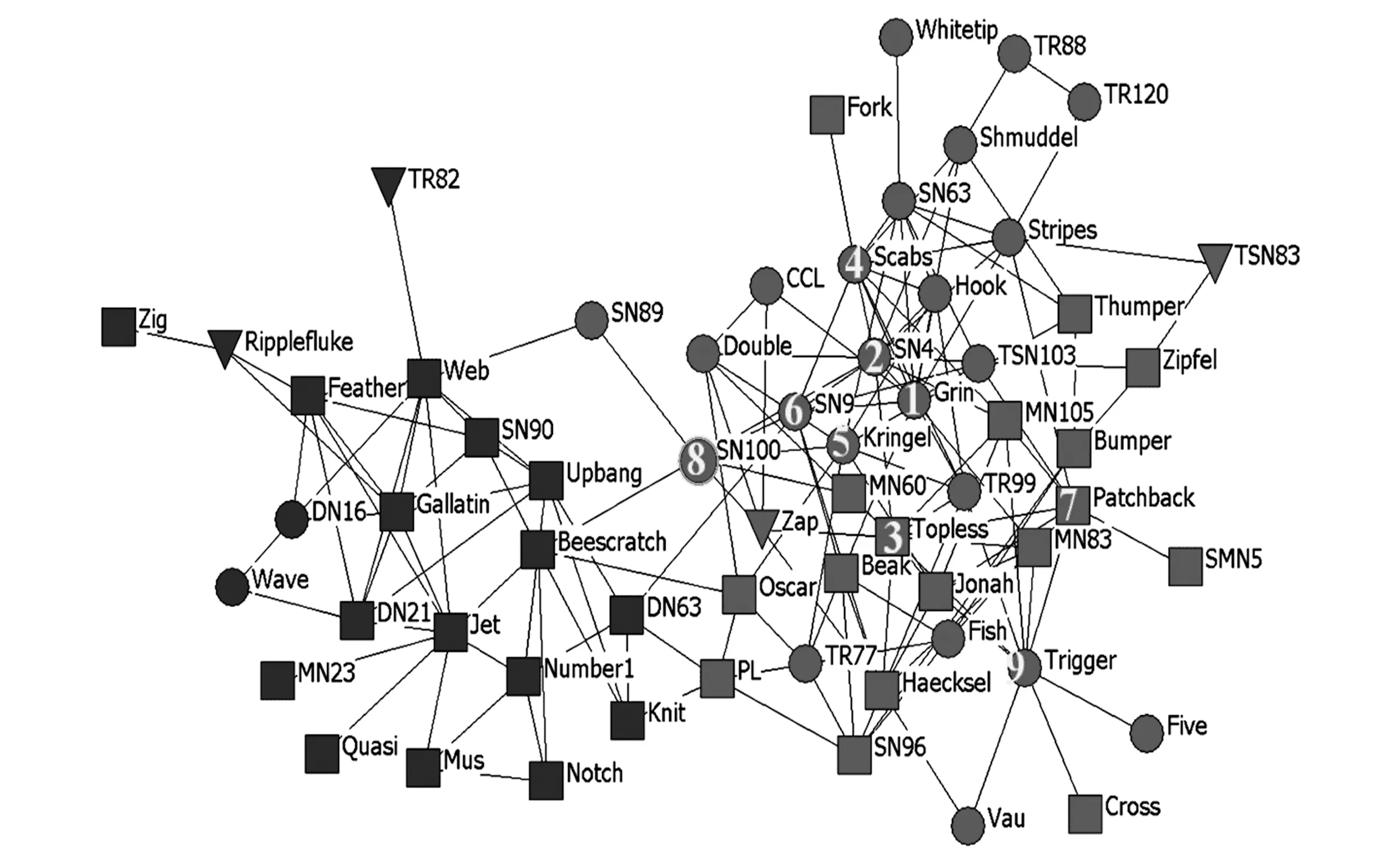
图3　Dolphin宽吻海豚家族关系网络

(3) 亚马逊图书销售网络

亚马逊图书销售网络由105个节点441条边组成[11]，其中节点为各类书籍名称，边为一个人如果同时购买2本书，则2本书之间有一条边。Mark Newman根据节点的类型，以及Amazon网站购买者的评论，将节点标记为“自由派”、“中立派”和“保守派”三类。其中49本书被标记为“保守派”，43本书被标记为“自由派”，13本书被标记为“中立”。

3.2相关算法实验结果

在Zarchary俱乐部球员的关系联接图中，节点1是俱乐部主管(校长)，节点34是俱乐部教练。那么节点3扮演什么角色呢？我们查阅了一些相关文献，发现中科院数学与系统学院章祥荪[12]和Amaral实验室Andrea Lancichinetti等[13]也对这一问题给出了他们的解答。章祥荪等给出的结果是节点1与节点9、10、31分别是3个社区的交叠节点，属于脆弱节点，如图4所示。Andrea Lancichinetti等提出了多级结构分析方法，在对Zarchary网络进行分析时给出的结果显示，分属于校长社团的节点14和分属于俱乐部教练社团的节点3、9、10、31是2个社区的交叠部分，属于脆弱节点，如图5所示。

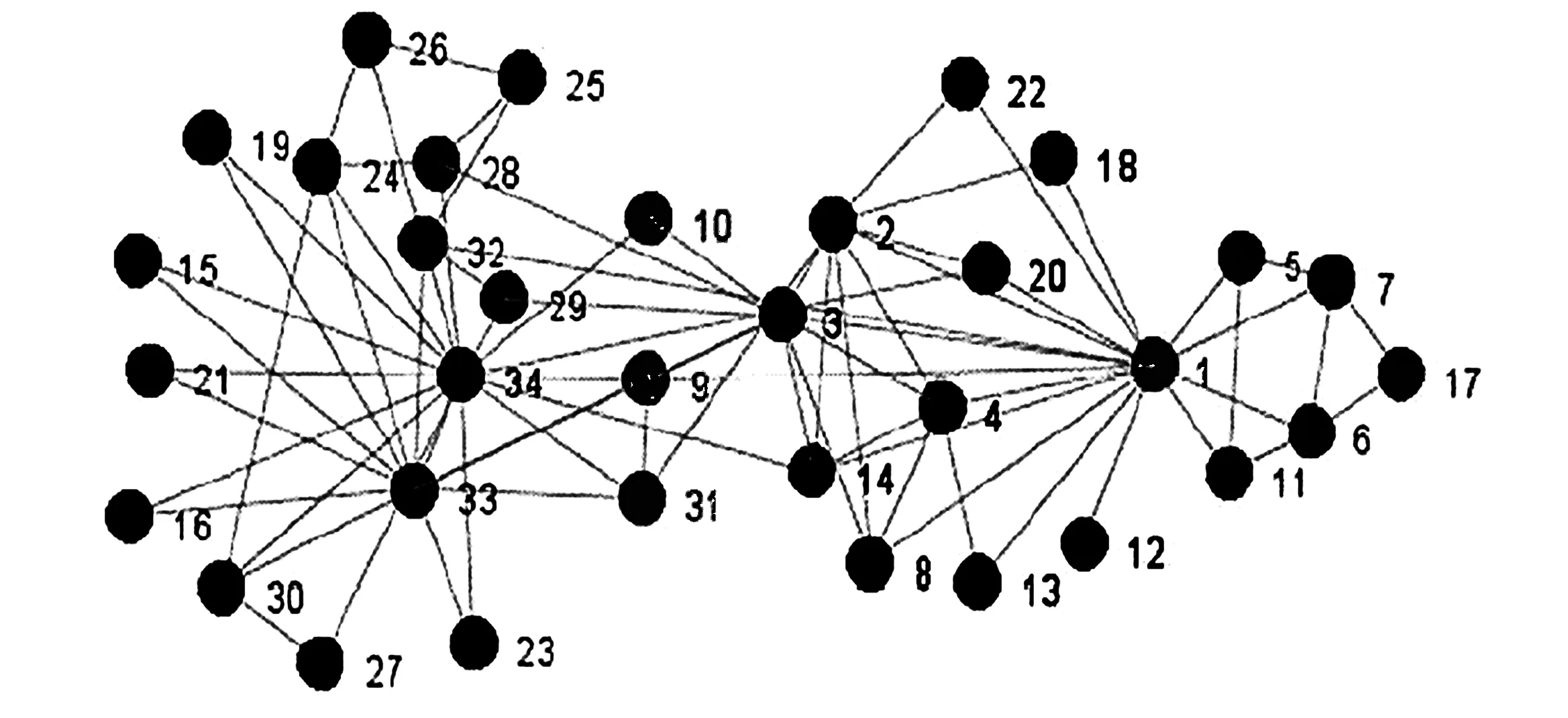
图4　中科院数学与系统学院章祥荪等给出的脆弱节点角色发现结果

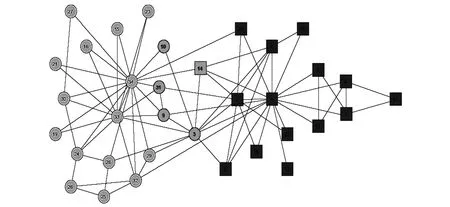
图5　多级结构分析方法对Zarchary网络的脆弱节点发现

3.3基于拓扑连接度的脆弱节点发现算法实验结果

实验中，分别对Zachary俱乐部网络、海豚网和亚马逊政治书销售网络进行了脆弱节点发现。

在Zarchary网络中，可以得到节点3、14、20属于2个社团的桥接节点(脆弱节点)，如图6所示。其中节点14与Andrea Lancichinetti的结果一致，节点8与节点20前面的分析方法均未能得到。节点3与两个社团的多个节点均有联接，属于周旋于2个社团的游离人士，属于典型的脆弱节点。节点20同时联接节点1(校长)和节点34(俱乐部教练)，与两个社团其他节点基本不联系，是传递两个社团核心节点之间消息的秘书节点，也属于脆弱节点。另一方面，如果将这3个节点移走，2个社团将出现明显的分裂，仅有3条联接，而前述算法均超过这一数量(或移走的节点数量过多)。因此，本算法给出的结果是正确的。

图7是对亚马逊书店政治书销售网络进行算法分析结构，可以看出节点5、8、50、52四个节点为脆弱节点。查阅这4个节点后发现，他们是圣经、炒股类书籍，属于经济、信仰和自然科学类，均不属于2个阵营，却为2个阵营共同购买。本算法获得结果与事实相符。

本文对Dolphines网络进行了分析，并给出了拓扑连接度的热力图，如图8所示。可以看出节点8、29、31、37的颜色最深，其拓扑连接度最低。因此，这4个节点应该属于2个社团的脆弱节点。其网络联接如图所示，如果移除这4个节点，Dolphines网络将会分裂为2个独立的网络。

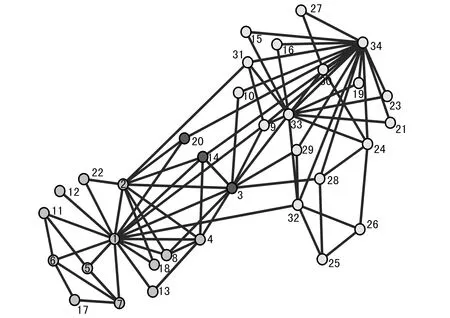
图6　Zarchary网络脆弱节点的发现

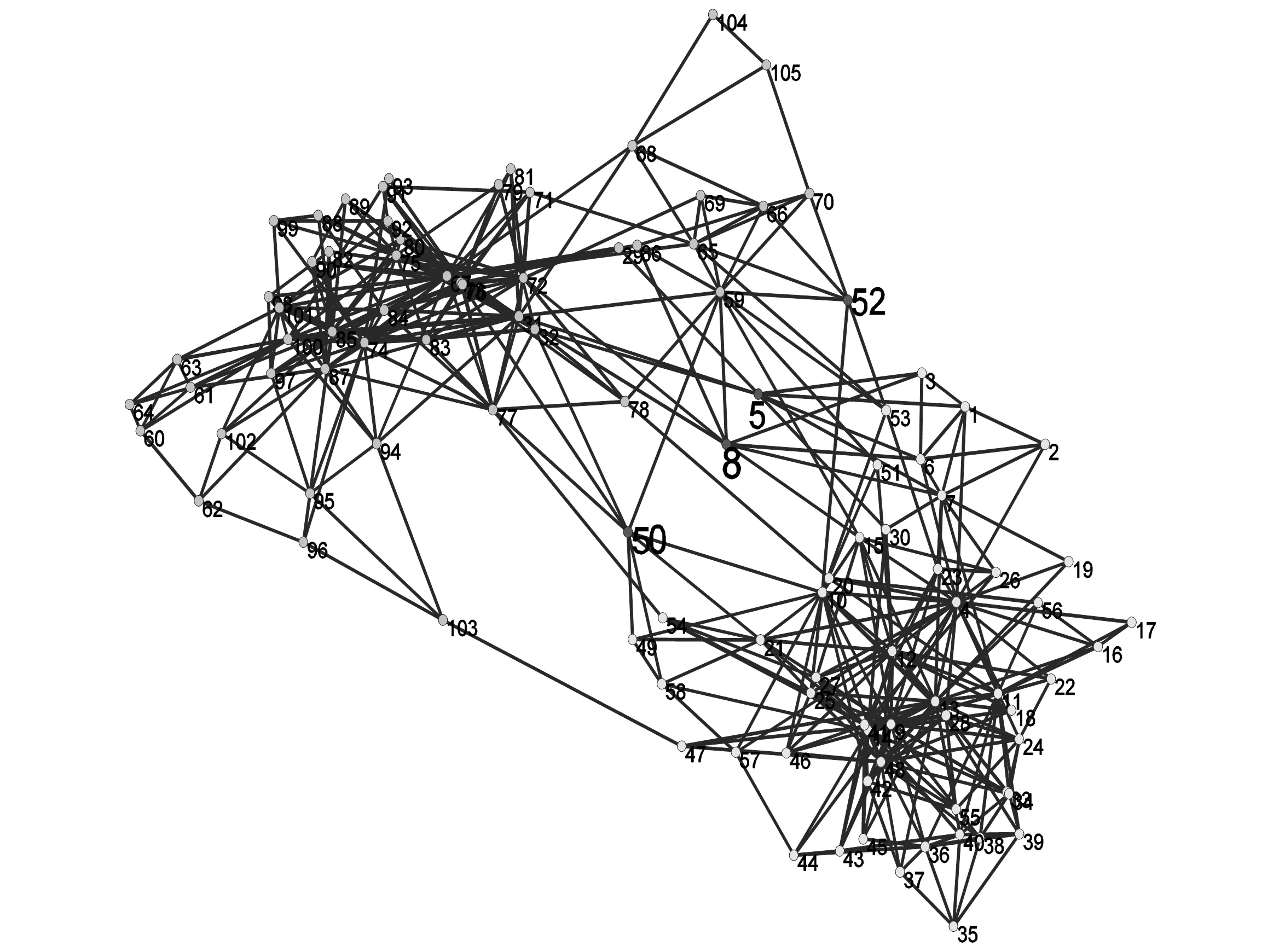
图7　亚马逊书店政治书销售网络脆弱节点的发现

图8　Dolphines网络拓扑连接度热力图

4　结束语

针对有目标性的网络攻击，本文提出了复杂网络的脆弱节点概念，创新性地引入Laplacian谱图理论，通过计算拓扑连接度并进行排序，发现网络中社团之间的关键桥接节点，为通信网络的抗毁性与鲁棒性研究提供了一种全新的思路。

[1]谭跃进,吕欣,吴俊,等.复杂网络抗毁性研究若干问题的思考[J].系统工程理论与实践,2008，28(增刊):116-120.

[2]Albert R,Barabási A L.StatisticalMechanicsof Complex Network[J].Review of Modern Physics,2002，74:47-97.

[3]Newman M E J.Modularity and Communities Structure in Networks[J].Proc.of the National Academy of Science,2006,103(23):8577-8582.

[4]Palla G,Derenyi I,Farkas I,et al.Uncovering the overlapping Community Structures of Complex networks in nature and society[J].Nature,2005,435(7043):814-818.

[5]尹峻松,肖 健,周宗谭,等.非线性流形学习方法的分析与应用[J].自然科学进展,2007,17(8):1015-1025.

[6]Belkin M,Niyogi P.Laplacian Eigenmaps and Spectral Techniques for Embedding and Clustering,Advances in Neural Information Processing Systems 14[M].Cambridge,MA:MIT Press,2002.

[7]Pothen A,Simon H,Liou K P.PartitioningSparseMatrices with Eigenvectors of Graphs[J].SIAM Journal on Matrix Analysis and Applications.1990,11(3):430-452.

[8]李德毅,杜 鹢.不确定性人工智能[M].北京：国防工业出处社,2005.

[9]Zachary W W.An Information Flow Model for Conflict and Fission in Small Groups[J].Journal of Anthropological Research,1977,33:452-473.

[10]Lusseau D,Schneider K,Boisseau O J,et al.The Bottlenose Dolphin Community of Doubtful Sound features a Large Proportion of Long-lasting Associations[J].Behavioral Ecology and Sociobiology,2003,54:396-405.

[11]Koschiitzki D,Schreiber F.ComparisonofCentralitiesfor Biological Networks [J].Proc.German Conf.Bioinformatics.2004,53(1):199-206.

[12]Zhang S,Wang R S,Zhang X S.Identification of overlapping Community Structure in Complex Networks Using Fuzzy C-means Clustering[J].Physica A Statistical Mechanics & Its Applications,2007,374(1):483-490.

[13]Lancichinetti A,Kivelä M,Saramäki J,et al.Characterizing the Community Structure of Complex Networks[J].Plos One,2010,5(8):11976-11976.

Novel Fragile Nodes Detection Algorithm for Complex Network Based on Laplacian Spectrum Analysis

YIN Jun-song,WANG Xiao-ming,ZHANG Xin-qiang,WANG Chun-jiang

(Chinese Institute of Electronic and SystemEngineering,Beijing 100141,China)

In the future net-centric information warfare,the node attack and cascading failure become important means for striking enemy information network,and seizing information superiority.In order to optimize the information infrastructure connection topologies,and enhance the network robustness and survivability,based on complex network topology connection matrix,the Laplacian spectrogram theory is introduced,and a novel fragile nodes detection algorithm for communication network is proposed,providing an effective brand-new thought of studying the robustness and invulnerability of information network.

complex network;community structure;Laplacian spectrum analysis;fragile node

10.3969/j.issn.1003-3114.2015.04.18

引用格式：尹峻松，王晓明，张新强，等.基于谱分析的复杂网络脆弱节点发现算法[J].无线电通信技术,2016,42(5):48-52.

2016-06-03

尹峻松(1978—)，男，博士，副研究员，主要研究方向：军事通信、指挥自动化、人工智能和复杂网络。王晓明(1978—)，男，硕士，工程师，主要研究方向：军事通信、指挥自动化、复杂网络。

TN915.08

A

1003-3114(2016)05-48-5