一种交流电弧炉通用性模型
2016-10-11畔陈红坤孙志达胡倩钱
胡 畔陈红坤孙志达胡 倩钱 龙
(1. 武汉大学电气工程学院 武汉 430072 2. 湖北咸宁供电公司检修分公司 咸宁 437100)
一种交流电弧炉通用性模型
胡 畔1陈红坤1孙志达1胡 倩1钱 龙2
(1. 武汉大学电气工程学院 武汉 430072 2. 湖北咸宁供电公司检修分公司 咸宁 437100)
交流电弧炉作为电力系统一种典型的冲击性、污染性负荷,严重地影响了电力系统的电能质量。其非线性、时变性和随机性的特点给电能质量的综合治理带来了严重的困扰。交流电弧炉工业用途的多样化,使得如何建立通用性模型来表征不同种类交流电弧炉电气特性成为现阶段研究的主要难点。首先从交流电弧炉能量耗散过程入手,分析不同工业用途下的交流电弧炉能量交换过程的共同特点,然后引入混沌现象来表征交流电弧炉负荷的不确定性机理,建立了交流电弧炉实用仿真模型。最后,依据现场实测数据,采用改进的遗传算法对模型中的参数进行了辨识,并对模型的正确性进行验证。研究结果表明,该通用性模型能够有效、精确地反映不同类型交流电弧炉的电气特性。
交流电弧炉 通用性模型 能量方程 混沌现象 参数辨识
0 引言
随着国民经济的发展,新型敏感设备(如各类精密加工生产线)的广泛应用对电能质量提出了更高的要求。交流电弧炉作为中高压配电网中一种典型的冲击性、污染性负荷,长期以来给电网电能质量带来了不可忽视的影响[1]。其非线性、不平衡、时变性和随机性的特点,给地区电网安全稳定运行带了巨大的挑战,严重制约着电网发展。因此,深入研究交流电弧炉用电特性,加强对交流电弧炉电能质量的综合治理,建立准确的交流电弧炉仿真治理系统及平台具有重要的研究意义。
文献[2,3]采用U-I特性曲线法将电压、电流的U-I特性曲线进行分段拟合,通过线性化得出交流电弧炉的静态模型。该类方法比较简单直接,交流电弧炉模型的参数不随供电系统参数(包括电压畸变和系统阻抗)的变化而改变,但由于交流电弧炉内部电压、电流不稳定,该类方法无法得到交流电弧炉的精确等效模型。文献[4]在对实际U-I特性曲线分段线性化的基础上,将带通白噪声叠加到等效电弧电阻上,模拟负载电阻的随机时变过程。文献[5]根据交流电弧炉中含有的混沌信号,将该信号叠加在U-I特性曲线上,建立了交流电弧炉模型。这类建模方法的效果还是比较满意的,主要问题是由于电弧炉系统本身的复杂,U-I特性曲线的结构和混沌信号的叠加系数难以确定。文献[6]从交流炼钢电弧的物理机理出发,提出一种交流电弧炉等效三相数学模型以及等效的非线性时变电弧电阻R的数学表达式。文献[7]在文献[6]的基础上,用粒子群算法(Particle Swarm Optimization, PSO)对交流电弧炉非线性电阻的参数进行参数辨识,其仿真结果同实际工况比较接近。但该模型的适应性不强,不能反映现今各类基于不同物理原理的交流电弧炉模型。
而随着工业科技的发展,交流电弧炉已经由传统单一的交流炼钢电弧炉,发展为具有多种工业用途的交流电弧炉,如铁合金炉、电石炉等。而传统建模方法,大多都是基于某种特定电弧炉的冶炼反应机理来建立的[8-11],这些方法在建立不同类型的三相交流电弧炉时,适应性不强,无法准确描述各类交流电弧炉的物理过程,建模效果不佳。因此,需要建立反映交流电弧炉特点的通用性模型,以适应不同工况的交流电弧炉要求。
因此,本文首先从交流电弧炉冶炼过程的机理出发,分析了炼钢电弧炉、铁合金炉和电石炉三种类型的交流电弧炉能量交换过程的一致性。然后,采用能量平衡方程以及混沌随机理论建立了描述交流电弧炉综合通用性动态数学模型。最后,通过采集湖北某地区典型交流电石炉厂的电压、电流数据,采用改进的遗传算法对上述交流电弧炉数学模型进行参数辨识。在Matlab/Simulink仿真环境下,证明了模型的准确性,并分析了该电石炉对电网的影响。仿真结果表明,本文提出的通用数学模型能够较准确地反映实际各种工业用途下三相交流电弧炉的物理变化过程,为进一步电能质量治理提供了依据。
1 交流电弧炉负荷通用数学模型
1.1交流电弧炉分类及能量交换分析
交流电弧炉是现代冶炼的重要手段,电弧炉主要分为交流电弧炉和直流电弧炉。交流电弧炉主要包括交流炼钢炉、电石炉和铁合金炉[12]。
(1)交流炼钢电弧炉负荷。交流炼钢炉是利用三相石墨电极和炉料之间产生电弧的热量冶炼金属。在炼钢的熔化期由于炉料与三相电极起弧不均匀以及炉料在熔化过程中崩落和滑动等因素,电弧电流具有很大的随机性。而还原期电弧燃烧比较稳定,电弧长度较长,电弧炉功率较稳定。
(2)电石炉负荷。电石生产的主要设备是电石炉,电石炉具有电阻电弧炉的特性,通过三相电极放电产生的高温融化兰炭和生石灰来生产电石。电石炉主要利用电极装置把电能转变成热能与化学能,通过能量交换生产冶炼电石、其工艺过程较复杂。
(3)铁合金炉。主要分为还原电炉和精炼电炉两类。①还原电炉:还原电炉又称埋弧电炉或矿热电炉,主要用来还原冶炼矿石,矿质还原剂及电石等化工原料。通过将电极插入炉料中,利用电弧的热量及电流通过炉料产生的能量来熔炼金属。某些生产工艺较为落后,通过人工控制电极插入炉料的深度来控制电流的大小。②精炼电炉:用于精炼中碳、低碳和微碳铁合金。电炉容量一般为 1 500~1 600kV·A,采用敞口固定或带盖倾动形式。前者类似还原电炉,可配备连续自焙电极;后者类似炼钢电弧炉,使用石墨或炭质电极。
三种类型的交流电弧炉,虽然冶炼方式、工业环境不同。但是其基本原理均是采用电弧放热来加工矿石,表1对比了不同种类电弧炉能量交换过程。
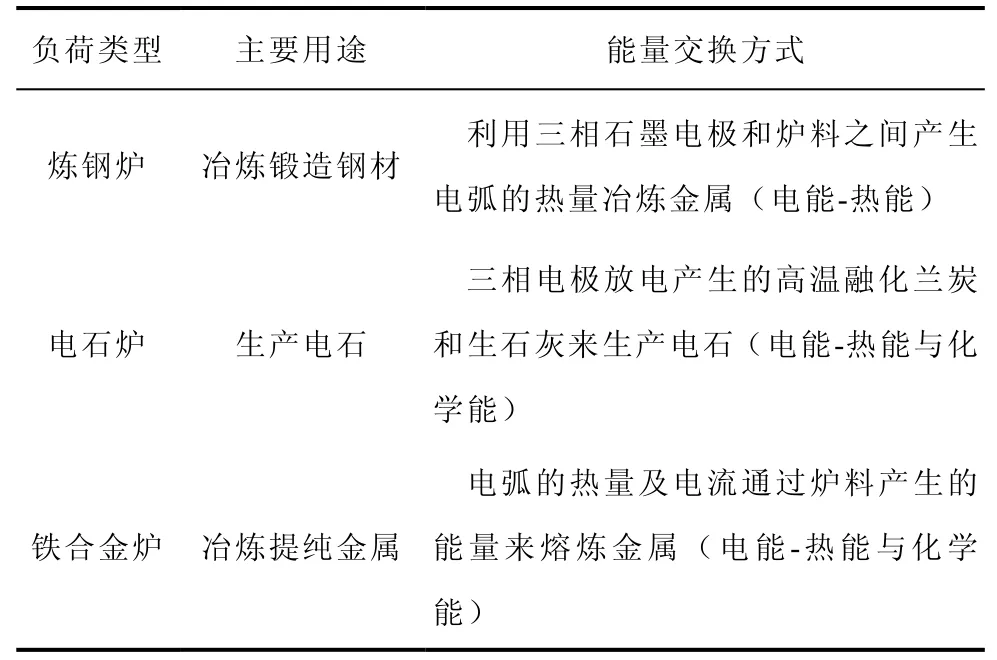
表1 交流电弧炉负荷特性分类Tab.1 Characteristic classification of EAF
因此,在冶炼的变化过程中三相电极的放电过程均满足能量守恒,只不过不同种类的交流电弧炉弧长能量交换方式不同,对应的能量方程中的参数不同。因此,在撇除不确定因素的条件下(如电弧不规则变化、燃烧不充分和人为干扰等)只要确定一组实际的运行参数,利用电极放电的能量方程,就能够确定实际某种特定用途的交流电弧炉模型。
1.2基于能量经验公式的交流电弧炉稳态模型
文献[13]研究了交流电弧炉能量交换过程,根据弧长变化特点,建立了相应的数学表达式。
弧功率平衡方程为

式中,p1为电弧炉对外散失的功率;p2为电弧炉能量交换功率;p3为电弧炉外部注入功率。
研究表明电弧对外散失的功率 p1可以表示为电弧半径的函数,其表达式为

式中,r为电弧半径;k1为待确定系数,根据电弧燃烧的温度以及电弧长短不同,n=0,1,2。
p2表示电弧炉能量交换功率,其大小同电弧弧长的导数成正比,同r2成正比,因此,其表达式为

式中,k2为常数。
由于电弧炉弧柱的电阻率同rm成反比,则得到

由式(1)~式(4)可以得到电弧炉以弧长 r为状态变量的表达式为

式(5)可以简化为

其中,电弧炉电压与电流的关系可以表示为

式(1)~式(7)中,参数k1、k2、k3、m和n为待确定的经验参数。其中m、n为整数,m,n=0,1,2;k1、k2和 k3为弧长变化固定系数,与不同种类的交流电弧炉有关,为主要待确定的参数。
运用该方程建立的交流电弧炉模型具有一定的局限性,这主要是未考虑电弧冶炼中的不确定性因素,如电极能量交换初期的电压、电流随机变化规律,因此只能表征稳态下的交流电弧炉运行状态。需要引入不确定性方程来表征交流电弧炉随机过程下的状态。
1.3基于蔡氏电路的混沌现象模拟
文献[14]的实时仿真结果表明,交流电弧炉冶炼过程中内部是含有混沌动态过程的。应用实测的电弧电压当前信号 x(t)、滞后时间 T 的信号 x(t+T)和滞后时间2T 的信号x(t+2T) 得出电弧电压三维相空间曲线,如图1所示。图1所示的相空间曲线展示出了一个不对称双涡卷混沌吸引子。

图1 相空间中的不对称双涡卷混沌吸引子[12]Fig.1 Phase space reconstruction of the asymmetric double-scroll chaotic attractor[12]
因此,采用混沌方程来表征交流电弧炉初期电极不确定性随机过程更能反映实际交流电弧炉冶炼过程。
为了仿真交流电弧炉内部的双涡卷混沌现象[15,16],本文采用了不对称非线性电阻的蔡氏电路[17]作为调制信号,来模拟交流电弧炉的内部混沌机理。
图2所示蔡氏电路主要包括线性电感L、可变线性电阻R、两个线性电容C1和C2,并有一个电压控制的不对称非线性电阻NR,不对称非线性电阻的伏安特性如图3所示。其中iL为流过电感L上的电流,iR为流经不对称非线性电阻NR上的电流,UC1、UC2为电容C1、C2上的端电压。该电路的基本原理是利用了不对称电阻产生的状态空间,从而形成三个互相作用的平衡点,产生不对称双涡卷状的混沌吸引子。选择iL、UC1和UC2作为系统状态变量,可得到基于不对称非线性电阻的蔡氏电路动力学状态方程组为
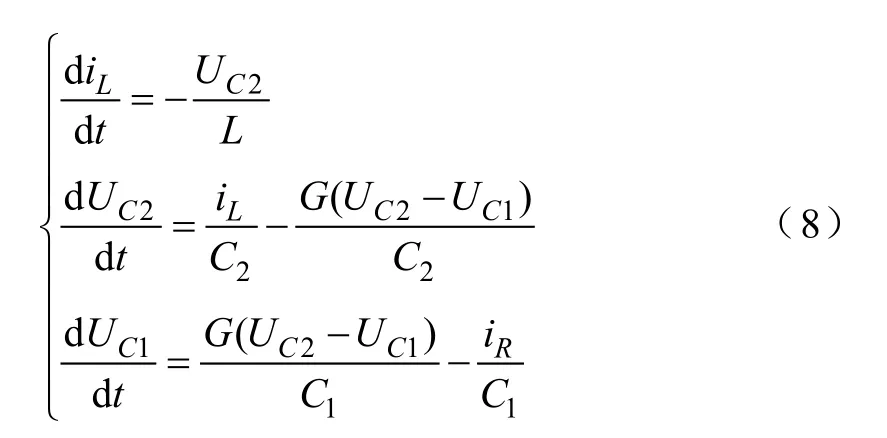
式中,G=1/R。

图2 蔡氏电路Fig.2 Chua’s circuit

图3 不对称非线性电阻伏安特性Fig.3 Volt-ampere characteristic of asymmetric nonlinear resistive element
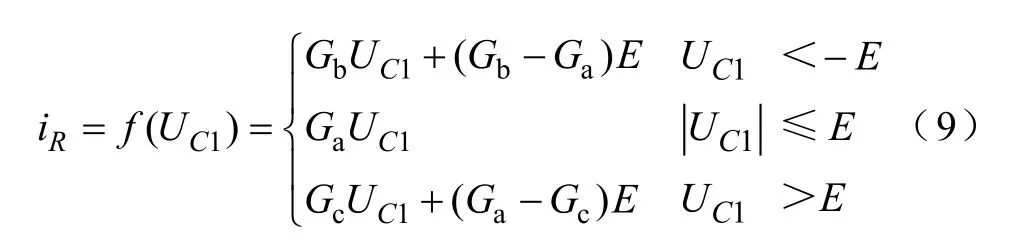
为了验证蔡氏电路的混沌现象,本文在Matlab/Simulink环境下,建立交流电弧炉混沌现象仿真模型,仿真结果如图4所示。可以观测到曲线图由直流平衡态经 Hopf分岔、倍周期分岔到单涡卷混沌吸引子,然后过渡到不对称双涡卷混沌吸引子的全过程,以及对应的的运动状态。
2 交流电弧炉参数辨识
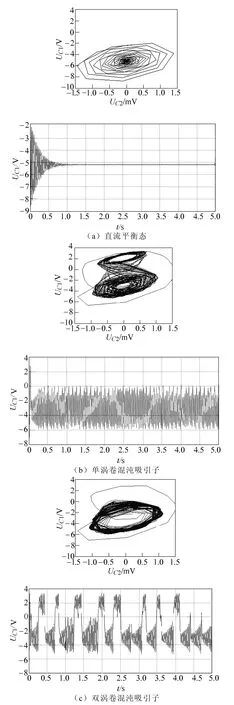
图4 混沌现象仿真结果Fig.4 Simulation results of chaos phenomenon
交流电弧炉是利用交流电在电极上产生的电弧来冶炼金属的一种设备。其建模的关键在于如何表征电极弧长的随机性变化过程。由于上文已经证明交流电弧炉随机变化过程中具有混沌特性,因此,本文通过在交流电弧炉能量方程上叠加动态混沌信号波,来模拟实际交流电弧炉的弧长的变化状态。
2.1交流电弧炉辨识数学模型
根据能量方程公式及混沌信号模型,本文将交流电弧炉负载等效成一个电流控制的电压源(CCVS),由电流计算电弧电压,其计算框图如图5所示。其中,η为混沌信号与能量方程的比例系数,k1、k2、k3、m和 n为能量方程中待确定的参数,其值表征交流电弧炉稳态条件下的能量交换方式。

图5 交流电弧炉参数辨识计算框图Fig.5 Calculation block diagram of EAF parameter identification
因此,为了寻找一组最优的参数向量使能量方程能够确定某实际交流电弧炉变化过程,本文采用参数辨识的方法予以确定。这里的目标函数取电弧电压计算与测量值的误差的二次方和最小。


式中,i满足状态方程

本文的约束规划方程为

式中,参数θ的约束为考虑到电弧电流过零点时滞后于外加激励的相位的约束。
2.2基于改进遗传算法的交流电弧炉辨识策略
本文采用文献[18]提出的改进遗传算法(Genetic Algorithm, GA)进行参数辨识。主要从改进选择方法、加入助长操作以及改进配对方法三个方面来优化算法效率。其中,改进选择主要采用两代竞争排序的选择方法来对遗传个体进行优选。加入助长操作则主要加入了一个助长算子来减小算法陷入局部最优可能。改进配对则是通过把适应度小的个体表现型编码的高位修改为与适应度大的个体表现型编码高位不同的值。
本算法以电弧电压作为辨识量,待辨识参数为k1、k2、k3、m、n及η。其中 m和 n为整数,取值为0,1,2,共有9种组合,程序中可作如下处理:将m和n的每种组合分别代入改进遗传算法种群,计算出目标函数值,最后取9种之中目标函数值最小的一组参数做为辨识结果。
由于待辨识参数为 k1、k2、k3、m、n及η,其参数数目少,但辨识范围大,因此采用二进制编码方式编码染色体,辨识结果精确到小数点后两位,η 精确到小数点后三位。图6为染色体构成。

图6 染色体构成Fig.6 Chromosome composition
参数辨识程序流程如图7所示,其计算过程包括种群初始化、选择、交叉、变异以及计算适应度值。通过在初始种群的产生、选择、交叉和变异等过程对遗传算法进行改进。
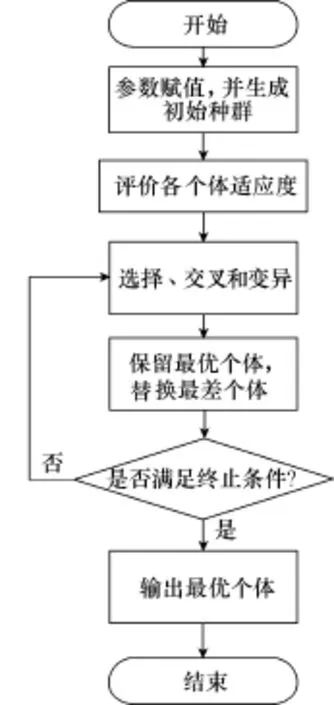
图7 改进遗传算法计算步骤Fig.7 Calculation steps of improved GA
3 仿真分析
由于交流电弧炉工业用途的复杂性,难以对各类模型均进行验证。考虑到能量平衡方程主要是根据交流炼钢电弧炉的物理特性提出的,且铁合金炉物理机理过程类似于炼钢及电石炉。因此,本文针对性地以咸宁某实际电石炉负荷作为主要的仿真研究对象,并采集了相关辨识数据。
该负荷供电起点为 110kV变电站,终点为110kV电石炉开关站,线路全长约2km,按110kV电压等级设计和运行,全线单回双分裂导线架设。导线型号为2 LGJ—240/30型钢芯铝绞线,全线双避雷,线路一侧地线选用型号为 GJ—70镀锌钢绞线,另一侧地线为10芯OPGW光缆,型号为OPGW—10B1/70。光缆进站采用普通光缆,型号为GYFTZY—10B1。
厂内有两台 12 500kV·A化学级工业交流电石生产线及配套设施(一主一备运行),电石炉主变容量12 500kV·A,其一次、二次侧额定电压分别为110kV 和144V。短网电感和电阻分别为0.7(pu)、0.721 5(pu)。其供电示意图如图8所示。

图8 湖北恩施某工业交流电石炉供电示意图Fig.8 Supply schematic diagram of an industrial calcium carbide furnace in EnShi, Hubei
3.1基于实测数据的电石炉参数辨识
采用故障录波仪分别采集电石炉主变一次、二次侧的电压、电流数据。由于实测数据中不仅包含电石炉负荷,还含有一定比例的其他负荷(如厂用电等)。因此,采用d5小波分析技术对实测数据进行滤波处理[19],去噪后得到辨识所需的实测数据(取其中2 543个点)。
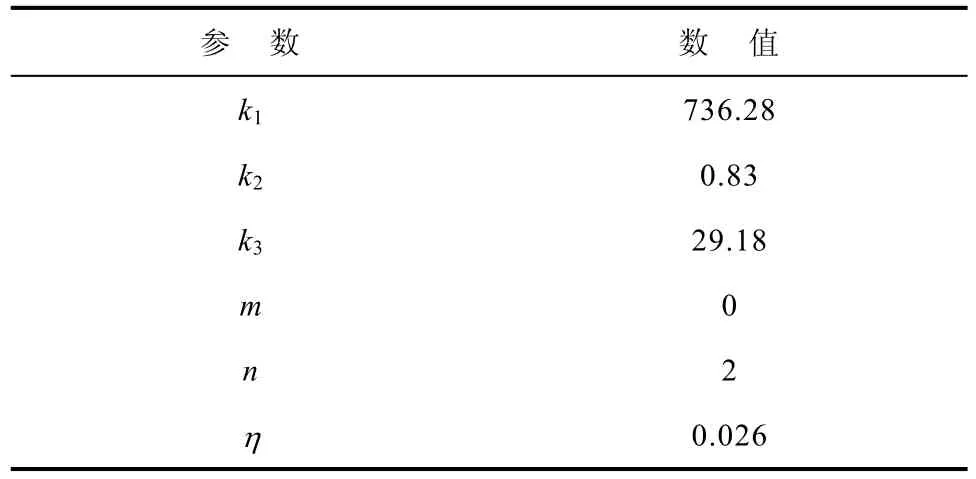
表2 参数辨识结果Tab.2 Results of parameter identification
采用改进遗传算法对电石炉解析模型进行参数辨识,辨识后参数见表 2,变压器二次电压辨识曲线结果如图9所示。

图9 电压辨识曲线Fig.9 Comparison of voltage identification curves
3.2电石炉引起的电能质量分析
为了验证该数学模型能否反映电石炉引起的电能质量问题,本文在Matlab/Simulink平台下根据辨识得到的参数,搭建电石炉仿真模型,并对电压波动、电压闪变及谐波参数进行仿真验证,仿真电路如图10所示。电石炉变压器直接与等效的供电系统相连,公共连接点对应电石炉变压器的一次侧母线;电石炉变压器一次绕组阻抗包括在一次侧串联阻抗内;二次侧串联阻抗包括电石炉变压器二次绕组阻抗、短网阻抗和电极阻抗。
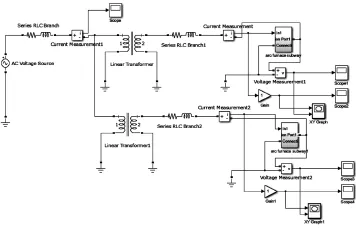
图10 电石炉仿真电路Fig.10 Simulation circuit of calcium carbide furnace
图10给出了电石炉主电路的拓扑结构,其基本结构同图8一致,电石炉负荷用等效的非线性阻抗表示。
对电石炉动态模型进行仿真分析,图11给出了该电石炉的U-I特性曲线,图12则给出了电石炉实测及仿真电流对比结果。
1)谐波含量对比及分析[20]
基于上述参数辨识结果,利用Matlab/Simulink的FFT分析功能对电石炉电压及电流各次谐波含量计算,表3及表4给出了实测及仿真谐波含量对比结果。

图11 电石炉U-I特性曲线Fig.11 Volt-ampere characteristic curves of calcium carbide furnace

图12 实测、仿真电流曲线比较Fig.12 Comparison of current curves between actual measurement and simulation

表3 电石炉电压谐波含量对比Tab.3 Comparison of voltage harmonic content

表4 电石炉电流谐波含量对比Tab.4 Comparison of current harmonic content
根据实测与仿真结果,各次谐波电压畸变率误差值不超过2.43%,总畸变率误差不超过3.06%。
根据实测与仿真结果,各次谐波电流畸变率误差值不超过1.36%,总畸变率误差不超过1.57%。
从仿真及实测结果来看,电石炉引起的谐波问题十分严重,其电压、电流畸变严重,严重超过了国标限值,应采用措施进行治理。
2)电压波动对比及分析
根据国标GB/T 12326—2008,电压波动定义为电压方均根曲线上相邻两个极值电压之差。根据以上定义电压波动的计算式为
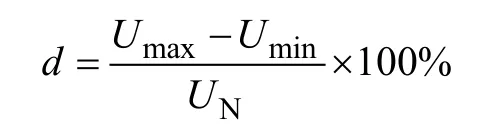
测得仿真模型中电压波动状况,其与实际测量值的对比状况见表5。

表5 仿真与实测电压波动对比Tab.5 Comparison between simulated voltage fluctuation and measured voltage fluctuation
由表5可得,实测电压波动及仿真电压波动的绝对误差为0.33。模型仿真结果与实测值基本接近。
3)电压闪变对比及分析
为了分析电石炉在公共 PCC引起的电压闪变情况,本文根据国际电工标准IEC 61000—4—15 提供的闪变仪测量方法及原理框图,结合文献[21,22]提供的统计评估方法,对瞬时视感度函数进行采样,对其累计密度概率函数进行处理,最后得出短时闪变值。仿真的闪变仪测试系统主要包括输入适配自检环节、平方解调环节、带通加权滤波环节和平方平滑滤波环节四个环节。
编译闪变评价文件Pst.mat函数,并在原电石炉模型上添加建立的闪变测试仪,闪变视感度仿真结果如图13所示。

图13 闪变视感度仿真结果Fig.13 Simulation results of the flicker sensation
根据测得的视感度函数计算电压短时闪变值。表6给出了电石炉实测及仿真闪变值的对比结果。

表6 仿真与实测电压闪变对比Tab.6 Comparison between simulated voltage flicker and measured voltage fluctuation
由表6可知,计算所得的Pst值为1.02。稍小于实测值,其绝对误差为 0.16%。该电石炉引起的短时间闪变Pst值稍稍大于国标规定(限值为1)。
4 结论
本文提出了一种采用能量平衡方程以及混沌随机理论建立了描述交流电弧炉综合通用性动态数学模型。
依据咸宁某电石厂现场实测数据,利用改进的遗传算法对本文提出的通用性模型进行了参数辨识,解决了能量参数模糊的问题,从而可以定性、定量地模拟实际状况。为进一步研究电能质量问题,提供了新的平台。
由于交流电弧炉种类繁多,本文只针对交流电石炉进行了验证,对于铁合金炉及炼钢炉还需要进一步的完善与验证。
[1] 石新春, 付超, 马巍巍, 等. 基于实测数据的电弧炉实时数字仿真模型及其实现[J]. 电工技术学报, 2009, 24(7): 177-182. Shi Xinchun, Fu Chao, Ma Weiwei, et al. A real-time digital simulation model and its implementation for arc furnace based on recorded field data[J]. Transactions of China Electrotechnical Society, 2009, 24(7): 177-182.
[2] 王晶, 束洪春, 林敏, 等. 用于动态电能质量分析的交流电弧炉的建模与仿真[J]. 电工技术学报, 2003, 18(3): 53-58. Wang Jing, Shu Hongchun, Lin Min, et al. Modeling and simulation of AC arc furnace for dynamic power quality studies[J]. Transactions of China Electrotechnical Society, 2003, 18(3): 53-58.
[3] Cox M D, Mirbod A. A new static arc compensator for an arc furnace[J]. IEEE Transactions on Power Delivery, 1986, 1(3): 110-120.
[4] Ozgun O, Abur A. Flicker study using a novel arc furnace model[J]. IEEE Transactions on Power Delivery, 2002, 17(4): 1158-1163.
[5] 王育飞, 姜建国. 用于电能质量研究的新型交流电弧炉混沌模型[J]. 中国电机工程学报, 2008, 28(10): 106-110. Wang Yufei, Jiang Jianguo. New AC electric arc furnaces for power quality study of chaos model[J] Proceedings of the CSEE, 2008, 28 (10): 106-110.
[6] 刘小河. 电弧炉电气系统的模型、谐波分析及电极调节系统自适应控制的研究[D]. 西安: 西安理工大学, 2000.
[7] 张恺伦, 陈宏伟, 江全元. 电弧炉负荷的三相综合建模与参数辨识[J]. 电力系统保护与控制, 2012, 40(16): 77-82. Zhang Kailun, Chen Hongwei, Jiang Quanyuan. Modeling and parameter identification of electric arc furnace load[J]. Power System Protection and Control, 2012, 40(16): 77-82.
[8] Gol M, Salor O, Alboyacy B, et al. A new fielddata-based EAF model for power quality studies[J]. IEEE Transactions Industry Application, 2010, 46(3): 1230-1242.
[9] Horton R, Haskew T A, Burch R F, A time-domain AC electric arc furnace model for flicker planning studies[J]. IEEE Transactions on Power Delivery, 2009, 24(3): 1450-1457.
[10] 池伟, 张恺伦, 查蕾, 等. 基于能量平衡的电弧炉模型的仿真与参数辨识[J]. 机电工程, 2012, 29(4): 454-457.Chi Wei, Zhang Kailun, Zha Lei, et al. Modeling and parameter estimation of arc furnace model based on energy conservation[J]. Journal of Mechanical & Electrical Engineering, 2012, 29(4): 454-457.
[11] 鲁军, 霍金彪, 张广跃. 电弧炉电极调节系统的模糊解耦控制器[J]. 电工技术学报, 2015, 30(12): 27-33. Lu Jun, Huo Jinbiao, Zhang Guangyue. Fuzzy decoupling controller on electrode regulator system of electric arc furnace[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 27-33.
[12] 刘军成. 电能质量分析方法[M]. 北京: 中国电力出版社, 2011.
[13] Acha E, Semlyen A, Rajakovic N. A harmonic domain computational package for nonlinear problems and its application to electric arcs[J]. IEEE Transactions on Power Delivery, 1990, 5(3): 1390-1397.
[14] King P E, Ochs T L, Hartman A D. Chaotic response in electric arc furnaces[J]. Journal Applied Physics, 1994, 76(4): 2059-2065.
[15] 黄润生, 黄浩. 混沌及其应用[M]. 武汉: 武汉大学出版社, 2005.
[16] Lori'a A. Robust linear control of (chaotic) permanentmagnet synchronous motors with uncertainties[J]. IEEE Transactions on Circuits and Systems-I, 2009, 56(9): 2109-2122.
[17] Matsumoto A. A chaotic attractor from Chua’s circuit[J]. IEEE Transactions Circuits System, 1984, 31(12): 1055-1058.
[18] 韩民晓, 马杰, 姚蜀军, 等. 改进的遗传算法辨识综合负荷模型[J]. 电力系统及其自动化学报, 2011, 23(3): 79-83. Han Mingxiao, Ma Jie, Yao Shujun, et al. Improve genetic algorithm and its application to composite load model[J]. Proceedings of the CSU-EPSA, 2011, 23(3): 79-83.
[19] 葛哲学. 小波分析理论与 Matlab R2007实现[M].北京: 电子工业出版社, 2007.
[20] 国家技术监督局. GB/T 14549—1993. 电能质量公用电网谐波[S]. 1993-7-31.
[21] 中国国家标准化管理委员会. GB/T 12326—2008.电能质量电压波动和闪变[S]. 北京: 中国标准出版社, 2008.
[22] 郭晓丽, 陈劲操. 电压波动和闪变的检测与分析[D]. 南京: 南京理工大学, 2004.
A Versatility Model of AC Electric Arc Furnace
Hu Pan1Chen Hongkun1Su Zhida1Hu Qian1Qian Long2
(1. School of Electrical Engineering Wuhan University Wuhan 430072 China 2. Maintenance of Hubei Xianning Power Supply Branch Company Xianning 437100 China)
As a typical impact and pollution load in power systems, electric arc furnace (EAF) seriously affects power quality. The characteristics of nonlinearity, time-variation, randomness increase the difficulty in comprehensive improvement and harness of power quality. Due to the diverse usage of industrial electric arc furnaces, it is difficult to build accurate versatility model that can reflect the electrical characteristics of different types of EAF currently. Firstly, the process of energy dissipation is analyzed, which proves the consistency of EAF energy exchange process under different industrial usages. Subsequently, chaos phenomenon is introduced to reflect the stochastic smelting process of EAF, and the practical simulation model is established. Finally, improved genetic algorithm is used to identify the model parameters based on practical measured data. The results show that the model can effectively and accurately reflect the characteristics of different types of electric arc furnaces.
Electric arc furnace, accurate versatility model, energy balance equation, chaos phenomenon, parameter identification
TM924.4
胡 畔 男,1989年生,博士研究生,研究方向为电能质量分析、电力系统运行与控制。
E-mail: 314784284@qq.com(通信作者)
陈红坤 男,1967年生,教授,博士生导师,研究方向为电力系统运行与控制、电能质量分析和新能源规划。
E-mail: chkinsz@163.com
2014-08-25 改稿日期 2015-04-08
