基于齿部磁场分析的大型潜水电机气隙偏心故障研究

鲍晓华 吕 强 王汉丰

（合肥工业大学电气与自动化工程学院 合肥 230009）

基于齿部磁场分析的大型潜水电机气隙偏心故障研究

鲍晓华 吕 强 王汉丰

（合肥工业大学电气与自动化工程学院 合肥 230009）

大型潜水电机广泛用于工矿企业给排水、城市污水处理等场所，然而转轴弯曲、轴承磨损等机械故障会引起气隙偏心。气隙偏心轻则导致气隙磁场畸变、振动增大和电流波动，重则定、转子相摩擦，导致设备停机或损坏。由此推导了大型潜水异步电机动态气隙偏心状态下某一固定位置处的定子齿部磁通解析表达式，分析偏心状态下的磁通故障频率，其基本思想是认为定、转子合成磁动势和气隙磁导决定了气隙磁通的大小，而定子齿部对应位置处气隙中的磁通全部经过齿进入定子轭部，据此提出了基于齿部磁场分析的大型潜水电机气隙偏心故障在线监测方法。最后，利用有限元法对理论分析进行了验证，并对故障频率的幅值与偏心度之间的关系作了进一步探索，为异步电机动态气隙偏心的精确检测提供了依据。

潜水电机 动态气隙偏心 磁场分析

0 引言

大型潜水电机多用于拖动水泵等大型机械，目前使用最为广泛的潜水电机是笼型异步电机。据统计[1]，笼型转子异步电机主要故障形式可分为定子绕组匝间短路、转子断条和气隙偏心三种。其中，气隙偏心可以分为静态偏心、动态偏心和混合偏心。静态偏心的位置不随转子的旋转而改变；动态偏心的位置在空间是变化的；混合偏心则是动、静态偏心共存的形式。在旋转电机中，静态偏心是固有存在的。因此，在实际中动态偏心和静态偏心往往是共存的[2]。对于主要尺寸比较大的矿用潜水电机，气隙偏心故障更为值得关注。

针对异步电机气隙偏心故障的在线监测与诊断问题，国内外学者做了大量工作。发展至今，按照故障监测量分类主要包括电流监测[3-6]、振动监测[7,8]、磁场监测[9-11]和电压监测[12]。电流监测是笼型转子异步电机最常见的检测方式，传统电流监测法的故障频率受定子绕组极对数和转子导条数的组合影响，且基波附近的故障信号容易被淹没；此外，对于轴向变化的气隙偏心，电流监测法具有一定的局限性[13]。振动监测可以弥补电流监测法的一些不足，但易受周围环境的干扰。电压监测是在电机断电瞬间测得定子电压以检测偏心，不能实现在线监测。磁场监测法目前仍处于发展初期，虽然磁场的检测略有不便，但能够更为精确地反映电机运行的不对称，随着技术的发展，以磁场为监测量的优势会逐渐体现出来。国内外对电机偏心磁场均进行了相关研究，文献[14]对混合偏心状态下的气隙磁通进行了详细的分析，从理论上得到了一系列气隙偏心相关的磁场故障频率，为基于磁场分析的气隙偏心检测提供了理论基础。文献[15]计算了大型水轮发电机的偏心磁场，发现偏心导致的电磁参数变化规律与偏心的性质有关。针对笼型异步电机，文献[9]基于法拉第电磁感应定律提出了一种采用径向磁通传感器的气隙偏心检测方法，比较了偏心和健康状态下测得的感应电动势波形，以此为偏心检测依据，并通过实验进行了验证。但其他故障形式，如转子断条，同样可能会引起电动势波形的畸变，要进行精确检测，还需做进一步的工作。文献[11]提出了采用外磁场来检测笼型异步电机气隙偏心等转子故障，其原理是利用故障时的轴向磁通变化，为基于磁场的气隙偏心检测提供了新的思路。

本文以大型潜水异步电机为研究对象，采用磁动势-磁导的方法，分析了动态气隙偏心状态下定子某一位置处的齿部磁场特征，并以此为偏心监测量，探索异步电机动态气隙偏心的准确检测机理。与传统的其他测量方法相比，引入了新的磁场特征量，表达式更为准确，并且适合实际检测模型。

1 异步电机偏心磁场奇异性分析

基于齿部磁场分析的气隙偏心检测方法集中于定子的某一个齿，设该齿位于定子侧圆周坐标θ 处。由于异步电机气隙较小，根据磁通的连续性，可近似认为θ 位置处的气隙磁场与该齿部磁场特征相同，因此可以通过分析气隙磁场来间接分析相应齿部磁场。

旋转电机动态气隙偏心形式如图1所示，O1为定子圆心，O2为转子圆心，电机运行时转子以 O1所在轴线为旋转轴。于是气隙长度可表示为[2]

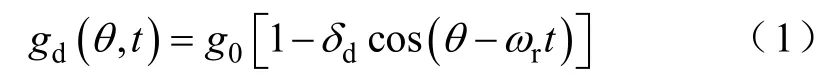
式中，g0为平均气隙长度，即电机正常时的气隙长度；ωr为转子角速度；θ 为定子侧角位置；t为时间；δd为动态偏心度，计算式为

式中，lO1O2为定子圆心与转子圆心间的距离。

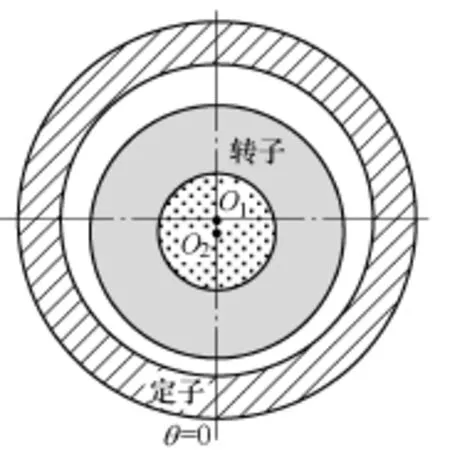
图1　旋转电机动态气隙偏心Fig.1 Dynamic air-gap eccentricity of the rotational electrical machine

通过展开成傅里叶级数，动态偏心状态下θ处的气隙磁导可写成

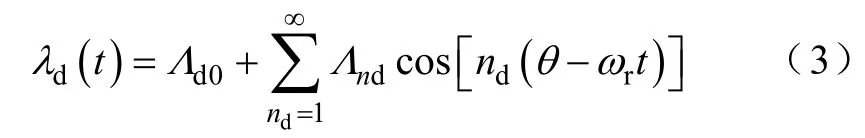
式中，d0Λ 为不考虑开槽效应的平均气隙磁导；dnΛ为第nd次磁导谐波的幅值。考虑转子开槽效应时，对应的磁导可写成同样的形式，即

式中，rt0Λ为与转子开槽对应的磁导平均值；rtnΛ为第nr

t次磁导谐波的幅值；R为转子导条数。

结合式（3）和式（4）并忽略饱和的影响，则总的气隙磁导为

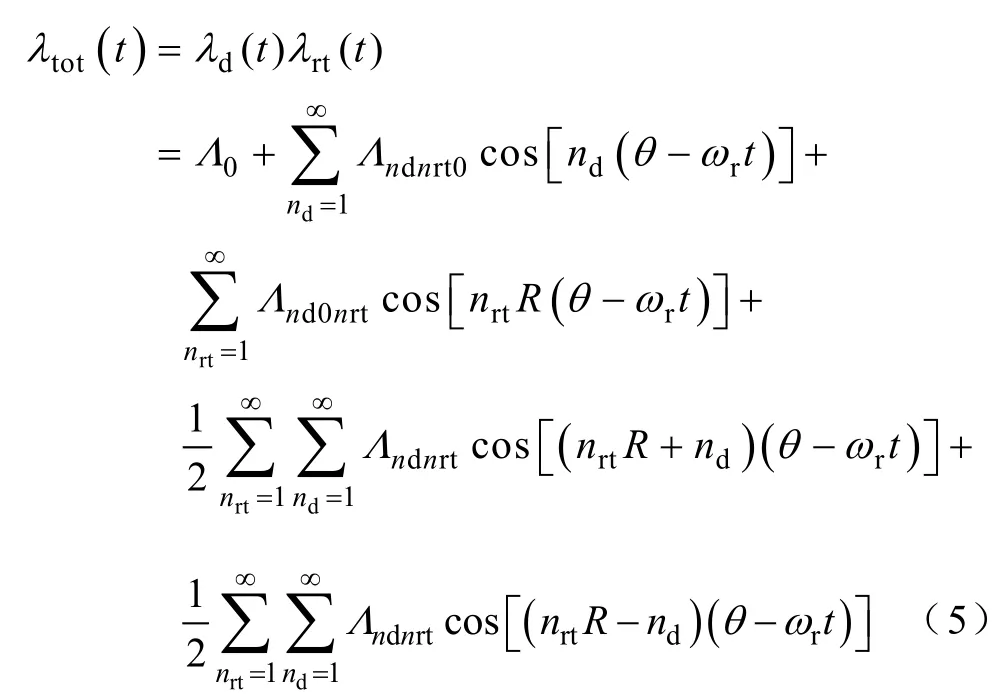
式中，0Λ为总气隙磁导平均值。

由定、转子电流产生的合成磁动势[14]为

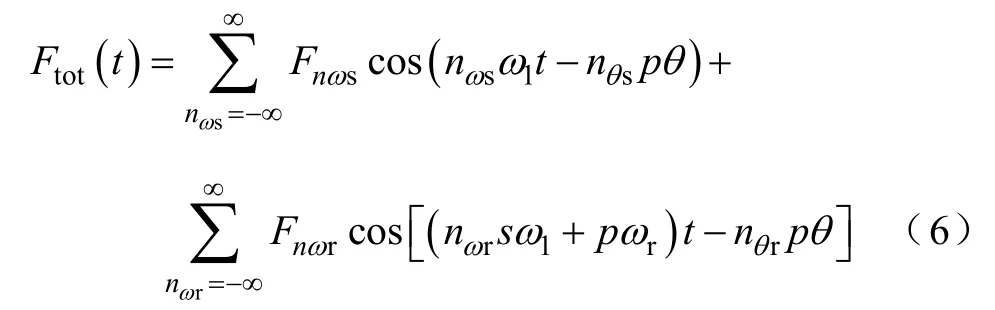
式中，nωs为定子磁动势时间谐波；nθs为定子磁动势空间谐波；Fnωs为第nωs次定子磁动势谐波幅值；nωr为转子磁动势时间谐波；nθr为转子磁动势空间谐波；Fnωr为第 nωr次转子磁动势谐波幅值；ω1为电源基波角频率；s为转差率；p为极对数。

联立式（5）和式（6），可得到θ 处的气隙磁通密度为

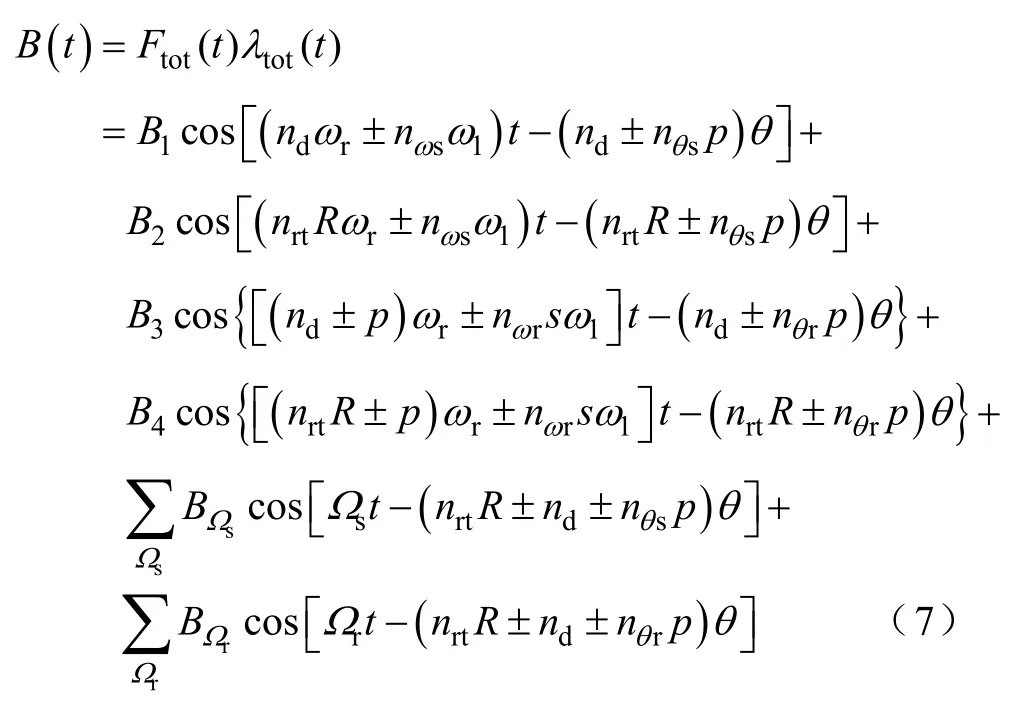
其中

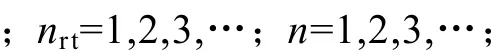
式中，f1为电源基波频率nωs=±1,±3,±5,…。若滤除转子开槽产生的谐波频率，由式（7）可得动态偏心故障的磁场特征频率为

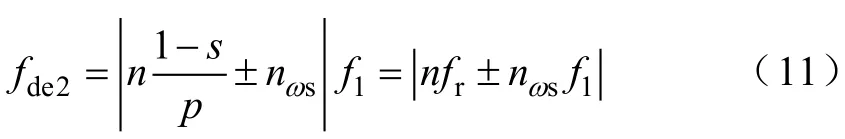
针对动态偏心，式（11）给出的特征谐波在以前所给出的定子电流检测方法中并不存在。但经过以上分析，该特征谐波存在气隙磁场中，相应地也存在于定子齿部磁场中。因此，动态气隙偏心下的故障频率可以分为两部分：①与转子开槽相关的槽谐波频率；②纯粹动态偏心导致的谐波频率。

2 有限元分析

本文通过有限元分析方法对一台型号为YBQ1200的大型高压潜水电机进行磁场分析，外观如图2所示，主要技术参数列于表1中。仿真模型如图3所示，模型中设置了磁场监测线圈，它是一个绕定子齿部若干匝的零电流激励绕组。磁场检测线圈位于θ =0处的定子齿顶部，检测线圈的磁链曲线即反映了θ =0处齿部磁场的变化情况。

图2　大型高压潜水电机Fig.2 Large high-voltage submersible motor

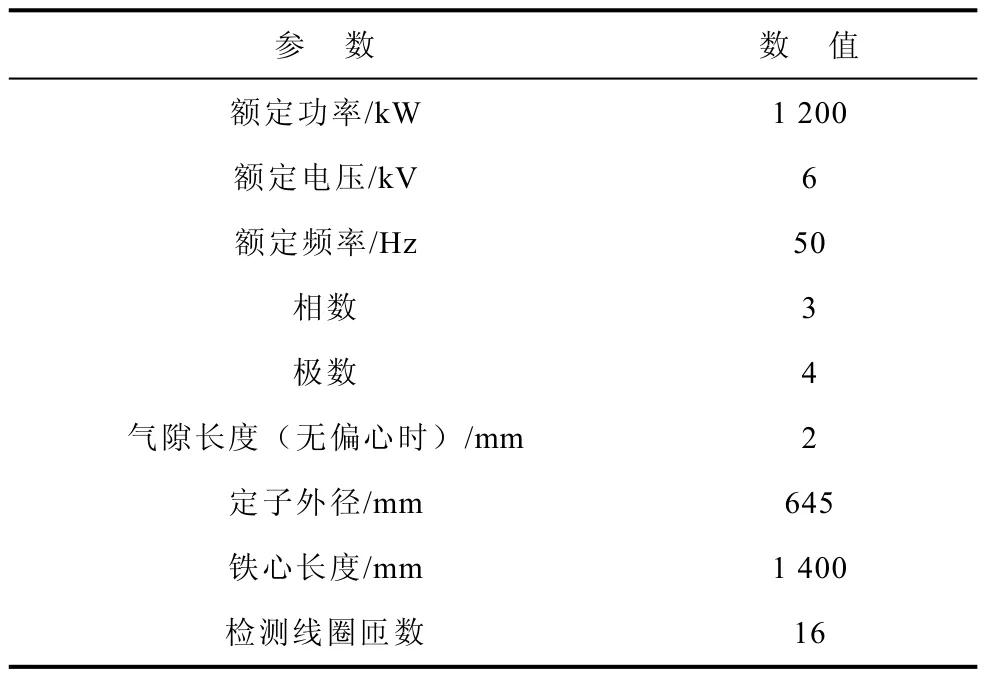
表1　仿真电机的技术参数Tab.1 Technical parameters of simulated motor

图3　潜水电机有限元模型Fig.3 Finite element model of the submersible motor

考虑到采用电流为监测量时不同p-R关系对检测性能的影响[1]，仿真过程中采用了 42、43和 44三种不同的转子导条数，获得了50%动态气隙偏心情况下检测线圈的磁链频谱，并与健康状态下的频谱进行了比较，结果如图4所示。其中1～8号幅值较为明显的故障频率分别对应为 f1−fr、f1+fr、3f1−fr、3f1+fr、[(R+1)(1−s)/p+1]f1、[(R+1)(1−s)/p−1]f1、[(R−1)(1−s)/p+1]f1和[(R−1)(1−s)/p−1]f1，符合理论分析的结果。

相比于电流检测法，为了突出检测齿部磁场法的优越性，图5给出了R=44，正常与50%动态偏心情况下定子电流频谱。由文献[1]可知，针对该电机，R=44时，与转子开槽相关的偏心特征槽谐波频率并不存在。图5中仿真结果符合该结论，因此电流检测并不适合于所有感应电机。另外，纯粹动态偏心导致的谐波频率也不存在于定子电流频谱中。但是，在如图4c所示的检测线圈磁链频谱中，该两种特征谐波频率都存在。由此可见，磁场故障特征频率的呈现并不受p-R关系的影响，适合于所有感应电机，且增加了新的特征谐波，如式（11）所示，与电流监测法相比有一定的优越性。

图4　检测线圈磁链频谱Fig.4 Flux linkage spectra of the detecting coil

图5 R=44时定子电流频谱Fig.5 Stator current spectra with R=44

图6显示了R=42时线圈磁链与定子电流频谱，易得 1～4号故障频率仅存在于线圈磁链频谱中，5～8号故障频率在线圈磁链与定子电流频谱都存在。但是，相比于定子电流频谱，在线圈磁链频谱中，由于5～8号故障频率尖峰更大，它们更易被观察。因此，相比于电流检测，齿部磁场检测特征谐波更易被观察，检测效果更好。

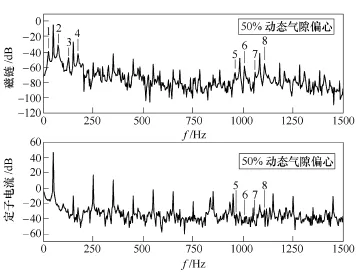
图6　R=42时线圈磁链与定子电流频谱比较Fig.6 Spectrum comparison between coil flux linkage and stator current with R=42

为了体现故障频率幅值随偏心度的变化情况，进一步分析了R=42时的8个较为明显的故障频率幅值与动态偏心度的关系，仿真结果如图7所示，1～8号频率分别对应为26.7Hz、73.3Hz、126.7Hz、173.3Hz、960.0Hz、1 006.7Hz、1 060.0Hz和1 106.7Hz。从仿真结果中可以看到，故障频率的幅值与偏心度基本成正比关系，其中基波频率附近的f1−fr(26.7Hz) 和f1+fr(73.3Hz)幅值较大，对于偏心程度的变化较为敏感；而与转子开槽相关的动态偏心故障频率（5～8号频率）幅值普遍较小，不适用于精确偏心检测。

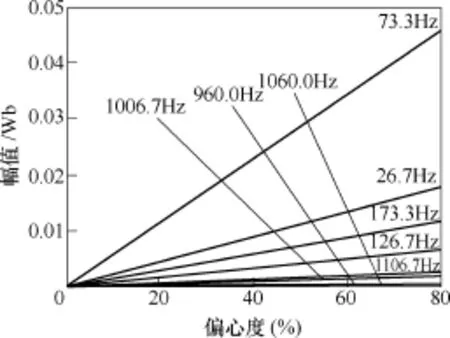
图7　故障频率的幅值-偏心度曲线Fig.7 Curves of amplitude against eccentricity degree with variation of the fault frequency

3 结论

本文推导了动态气隙偏心状态下大型潜水异步电机定子某一位置处的齿部磁场解析表达式，得到了偏心故障状态下的磁场时间谐波，并初步探索了这些故障谐波与偏心度的关系，为气隙偏心精确检测提供了一定的理论依据。主要得到以下结论：

1）以齿部磁场为监测量检测笼型异步电机动态气隙偏心不受电机极数和转子导条数配合的影响，克服了常见的以定子电流为监测量的缺陷。另外，相比定子电流法，该方法下线圈磁链频谱中的特征谐波更易检测。

2）在基波附近的纯粹动态偏心导致的谐波频率存在于齿部磁场中，用于检测动态偏心的特征谐波增加。

3）动态气隙偏心故障频率的幅值与偏心度近似呈正比关系，且基波附近频率为f1−fr和f1+fr的幅值随偏心度的变化较大，即比其他故障频率更为敏感，适合用于动态气隙偏心的精确检测。

[1] 刘振兴. 电机故障在线监测诊断新原理和新技术[M]. 武汉: 华中科技大学, 2004.

[2] David G, Thomson W T, Roach S. Analysis of airgap flux, current, and vibration signals as a function of the combination of static and dynamic airgap eccentricity in 3-phase induction motors[J]. IEEE Transactions on Industry Applications, 1997, 33(1): 24-34.

[3] Nandi S, Toliyat H A, Li Xiaodong. Condition monitoring and fault diagnosis of electrical motorsareview[J]. IEEE Transactions Energy Conver- sation, 2005, 20(4): 719-729.

[4] 宁玉泉. 大型三相异步电机气隙偏心的在线监测和故障诊断[J]. 大电机技术, 1999(6): 20-24. Ning Yuquan. On-line monitoring and fault diagnosing for eccentric gap of large 3-phase asynchronous machines[J]. Large Electric Machine and Hydraulic Turbine, 1999(6): 20-24.

[5] 孙立军, 吕志香, 刘海丽, 等. 基于DSO-2100的异步电机转子偏心故障检测与诊断[J]. 电机与控制学报, 2005, 9(6): 537-540. Sun Lijun, Lü Zhixiang, Liu Haili, et al. A detection and diagnostic system of rotor eccentricity in asynchronous motor with DSO-2100[J]. Electric Machinesand Control, 2005, 9(6): 537-540.

[6] Pires V F, Kadivonga M, Martins J F, et al. Motor square current signature analysis for induction motor[J]. Measurement, 2013, 46(2): 942-948.

[7] Dorrell D G, Cossar C. A vibration-based condition monitoring system for switched reluctance machine rotor eccentricity detection[J]. IEEE Transactions on Magnetics, 2008, 44(9): 2204-2214.

[8] Ebrahimi B M, Faiz J. Magnetic field and vibration monitoring in permanent magnet synchronous motors under eccentricity fault[J]. IET Electric Power Applications, 2012, 6(1): 35-45.

[9] Hwang D H, Han S B, Woo B C, et al. Detection of air-gap eccentricity and broken-rotor bar conditions in a squirrel-cage induction motor using the radial flux sensor[J]. Journal of Applied Physics, 2008, 103(7): 07F131(1-3).

[10] Vitek O, Janda M, Hajek V, et al. Detection of eccentricity and bearings fault using stray flux monitoring[C]//International Conference on Diagnostics for Electric Machines, Power Electronics & Drives, Bologna, 2011: 456-461.

[11] Ceban A, Pusca R, Romary R. Study of rotor faults in induction motors using external magnetic field analysis[J]. IEEE Transactions on Industrial Electronics, 2012, 59(5): 2082-2093.

[12] Nandi S, Ilamparithi T C, Sang B L, et al. Detection of eccentricity faults in induction machines based on nameplate parameters[J]. IEEE Transactions on Industrial Electronics, 2011, 58(5): 1673-1683.

[13] Li X, Wu Q, Nandi S. Performance analysis of a three-phase induction machine with inclined static eccentricity[J]. IEEE Transactions on Industry Applications, 2007, 43(2): 531-541.

[14] Cameron J R, Thomson W T, Dow A B. Vibration and current monitoring for detecting airgap eccentricity in large induction motors[J]. IEE Proceedings B-Electric Power Applications, 1986, 133(3): 155-163.

[15] 诸嘉慧, 邱阿瑞. 大型水轮发电机转子偏心磁场的计算[J]. 大电机技术, 2007(3): 1-4. Zhu Jiahui, Qiu Arui. Eccentric magnetic field calculation for a large hydrogenerator[J]. Large Electric Machine and Hydraulic Turbine, 2007(3): 1-4.

Study on Air-Gap Eccentricity Fault in Large Submersible Motors with Tooth Magnetic Field Analysis

Bao Xiaohua Lü Qiang Wang Hanfeng
（School of Electrical Engineering and Automation Hefei University of Technology Hefei 230009 China）

Large submersible motors are widely used for water supply and drainage of industry, municipal wastewater treatment, etc. However, mechanical failures such as bent shaft and bearing damages will result in air-gap eccentricity. Small air-gap eccentricity gives rise to air-gap field distortion, increase in vibration and current fluctuation. Critical air-gap eccentricity may lead to a rub between the rotor and stator, or breakdown of the driven equipment. This paper deduces the magnetic flux expression of a stator tooth in a dynamic eccentric submersible motor, and analyzes eccentricity related frequencies in tooth magnetic field. The basic idea is that the air-gap magnetic flux is determined by the air-gap permeance and magnetomotive force, while the air gap magnetic flux near the tooth totally passes through the stator tooth. Accordingly, a way of air-gap eccentricity detection in large submersible motors is proposed in this paper. Finally, the theoretical analysis is validated by finite element simulation. This paper also explores the relation between magnitude of harmonic and degree of eccentricity, providing the precise air-gap eccentricity detection of induction motors.

Submersible motor, dynamic air-gap eccentricity, magnetic field analysis

TM343

鲍晓华 男，1972 年生，博士，教授，博士生导师，主要从事电机噪声与振动的理论及控制技术的研究。

E-mail: baoxh@hfut.edu.cn（通信作者）

吕 强 男，1988年生，硕士研究生，主要从事电机设计和有限元分析方面的研究。

E-mail: lq_chance@163.com

国家自然科学基金资助项目（51177033、51377039）。

2014-04-22 改稿日期 2014-08-10