基于新型矢量选择表的电压型三电平中性点钳位整流器直接功率控制策略

李 宁王 跃王兆安

（1. 西安交通大学电气工程学院 西安 710049 2. 西安理工大学自动化与信息工程学院 西安 710048）

基于新型矢量选择表的电压型三电平中性点钳位整流器直接功率控制策略

李 宁1,2王 跃1王兆安1

（1. 西安交通大学电气工程学院 西安 710049 2. 西安理工大学自动化与信息工程学院 西安 710048）

在电压型三电平中性点钳位（NPC）整流器的控制策略中，直接功率控制（DPC）策略具有算法简单和动态性能好的优点。分析了电压型三电平NPC整流器DPC策略的基本原理，推导了系统瞬时功率与交、直流侧参数的关系，并研究了系统直流电压利用率对瞬时功率的影响，提出一类新颖的三电平NPC整流器DPC策略。该策略将系统直流电压利用率分成若干区域，在每个区域中选择不同的矢量选择表对系统瞬时功率进行控制。此外，通过合理选择DPC策略矢量表对应的开关状态，解决了三电平NPC整流器直流电容电压不平衡问题。最后，针对某些直流电压利用率区间内系统瞬时无功功率存在非正常波动问题，分析其产生原因，并通过添加过渡扇区及与之对应的矢量选择表格，对系统瞬时无功功率的非正常波动进行修正。仿真和实验验证了理论分析的正确性。

电压型三电平中性点钳位整流器 直接功率控制策略 直流电压利用率 直流电容电压不平衡 瞬时无功功率 非正常波动

0 引言

电压型三电平中性点钳位（Neutral Point Clamped, NPC）整流器是目前最常用的多电平整流器[1]，相比传统的两电平整流器，三电平整流器具有输出功率大、输出波形THD小、器件电压应力和系统EMI低等多方面的优点，因而被广泛地应用于各种中、高压大功率场合[2,3]。

20世纪90年代以来，针对三电平NPC整流器的研究有很多，其中，高性能控制策略是一个研究热点。目前，在三电平NPC整流器中，最常用的控制策略是电压定向控制（Voltage Oriented Control, VOC）策略。1983年，H. Akagi教授提出了著名的瞬时无功功率理论[4-6]，为新型电力电子变流器控制策略的产生提供了重要理论基础；20世纪 80年代中期，日本的 I. Takahashi教授和德国鲁尔大学的M. Depenbrock教授分别提出圆形直接转矩控制方案[7]和六边形直接转矩控制方案[8]；1991年，T. Ohnishi教授结合瞬时功率理论和直接转矩控制提出直接功率控制（Direct Power Control, DPC）策略[9,10]，该策略将瞬时有功功率和无功功率用于PWM 整流器闭环控制系统中，实现了对系统功率的精确控制。自此以后，DPC策略被不断地发展，并应用于各种电力电子变流器与各种环境中。

与VOC策略相比，DPC策略直接选择合适的矢量实现对瞬时功率的控制，因而具有算法简单和动态响应更好等优点[11-14]。然而，由于三电平NPC整流器的特殊性及矢量复杂性，DPC策略的应用远不如VOC策略广泛。在可见的三电平NPC整流器DPC策略研究文献中，主要的研究内容是瞬时功率求解、功率内环和电压外环三部分。在DPC策略瞬时功率求解中，主要研究点为瞬时功率的计算或估算方法；在功率内环模块中，传统DPC策略的主要研究点是根据控制需要改进DPC矢量选择表格，同时也有学者根据DPC策略开关频率不固定的特点，提出各种稳定开关频率的DPC方案；在电压外环的研究中，主要研究内容为外环控制器的设计，除了传统的比例积分（Proportional Integral, PI）控制器以外，目前应用的还有滑模变控制器和模糊控制器等[15-18]。但是，鲜有文章研究直流电压利用率这一重要指标对DPC策略矢量选择的影响。本文在三电平NPC数学模型的基础上，全面分析了三电平NPC整流器 DPC策略中直流电压利用率对矢量选择表的影响，针对不同的系统直流电压利用率区间，应用不同的矢量选择表对系统瞬时功率进行控制。在三电平NPC整流器中，直流电容电压波动也是一个亟待解决的问题，本文通过合理选择矢量选择表中各矢量对应的开关状态解决了三电平 NPC整流器存在的直流电容电压不平衡问题。针对在某些直流电压利用率区间内，应用现有矢量选择表会引起瞬时无功功率波动这一实际问题，本文分析了瞬时无功功率异常波动的原因，并通过添加过渡扇区及与之相关的矢量选择表格实现了瞬时无功功率的精确控制。最后，通过仿真和实验对本文的理论分析进行了验证。

1 三电平NPC整流器DPC系统数学模型

图1 三电平NPC整流器主电路拓扑等效电路Fig.1 Equivalent circuit of three-level NPC rectifier

图1为三电平NPC整流器等效电路。图中，每相桥臂的电路结构可以简化为一个与直流侧电容相通的单刀三掷开关。本节中将以该等效电路为基础，在三相电路平衡的情况下，推导三电平NPC整流器DPC策略的数学模型。图1中，ua、ub和uc为电网相电压，N为其参考点；Rs、Ls分别为线路等效电阻和网侧电感；ia、ib和 ic为三相电流；Sx(x=a,b,c)为开关函数，Sx=Sxy(y=p,o,n)时x相输出y电平；C1、C2为直流电容（C1=C2=C），uC1和 uC2为两电容的电压；ip和in分别为流入p点和n点的电流；iC1和iC2为流过直流电容的电流；LL和 RL分别为负载侧等效电感和电阻；iL为负载电流。

将图1中各量变换到两相同步旋转坐标系中，可得整流器的数学模型为

式中，ud、uq及id、iq分别表示三相电压ux和ix(x=a,b,c)在同步旋转坐标系中的对应值；Sdy和 Sqy分别为开关函数Sxy(x=a,b,c；y=p,n)在d、q轴上的对应值。

根据瞬时无功功率理论，三相电路瞬时功率为

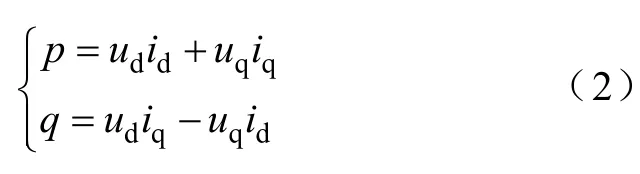
式中，ud和uq分别为电网电压的d轴和q轴分量。当d轴始终与参考电压矢量重合时，uq=0，此时瞬时功率的表达式为

由式（1）可知，在dq轴上，系统电压和电流满足

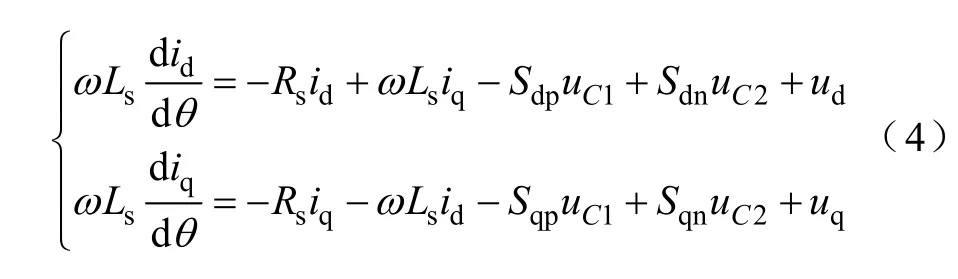
式中，ω为同步旋转坐标系的角速度；θ 为旋转坐标系转过的角度，θ =ωt。将式（4）的左右两边同乘以ud，并结合式（3）得

定义参考电压矢量在z（z=d,q）轴上的投影urz为

实际应用中一般忽略Rs项的影响，考虑到du=（U为相电压有效值），有

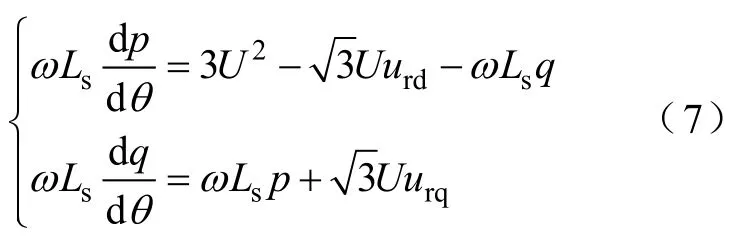
实际中为了简化分析难度，往往忽略式（7）中的耦合项[9,10,17]，则有

由式（8）可知，参考电压矢量在d轴的投影决定了系统瞬时有功功率增量，其在q轴的投影决定了系统瞬时无功功率增量，据此可以选择开关矢量对瞬时功率进行控制。

2 基于直流电压利用率的新型三电平DPC矢量选择表

图2为三电平NPC整流器DPC系统控制框图。图中，内环方案尤其是开关状态选择表是DPC系统的重要组成部分。本节着重分析各矢量对系统瞬时功率的影响。

2.1三电平NPC整流器各矢量对瞬时功率的影响

图3a为NPC型三电平整流器空间电压矢量分布，图中共有 6个幅值为的大矢量（Udc为三电平NPC整流器直流总电压，矢量长度求解时采用等功率变换矩阵），6个幅值为的中矢量，6个幅值为的个小矢量及一个零矢量。为了分析各矢量对瞬时功率的影响，将整个空间矢量图分为12个扇区（θ1～θ12），具体如图3b所示，文中将编号为奇数的扇区称为奇数扇区，编号为偶数的扇区称为偶数扇区。

图3　三电平NPC整流器电压矢量及DPC策略扇区划分Fig.3 Vectors and sector division of DPC system in three-level NPC rectifier

为了准确地分析功率与各参考电压矢量的关系，引入直流电压利用率η 表征交流侧线电压峰值和直流总电压Udc的比例关系

式中，η 的取值决定了参考电压矢量的运行区域，具体如图4所示。在DPC策略的矢量选择中，做如下设定：为了减小系统的损耗，降低du/dt，优先选择参考电压矢量所在大扇区（相邻大矢量围成三角形）中距参考矢量最近的合适矢量。如当参考电压矢量落在第1、2扇区时，先考虑由V0、VL1和VL2构成三角形中合适矢量。

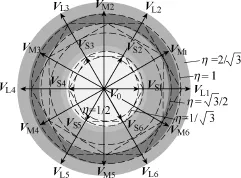
图4　三电平整流器各矢量与直流电压利用率η 的关系Fig.4 Relations between η and voltage vectors in three-level NPC rectifier

在三电平NPC整流器DPC中，定义参考电压矢量Vref与相电压Ux(x=a,b,c)的关系为

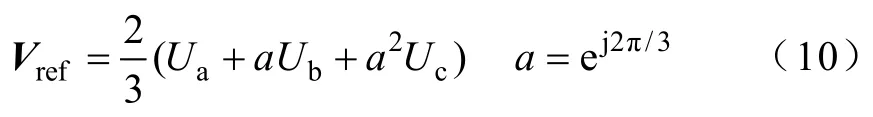
图5　三电平NPC整流器各矢量在dq轴上的投影Fig.5 The projection of each vector in dq axes of three-level NPC rectifier

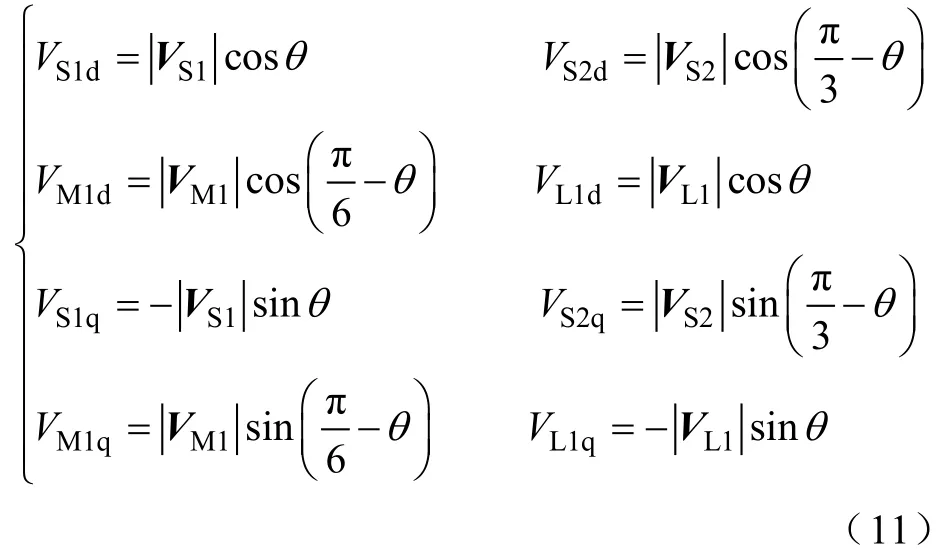
根据式（11），可以得到第一扇区中各矢量在dq轴上的投影长度范围，由式（8）可得各矢量对瞬时功率的影响，见表 1。其中，“+”表示选择该矢量可以使瞬时功率增加，“-”表示选择该矢量可以使瞬时功率减小，“※”表示选择该矢量对瞬时功率无影响，“*”表示选择该矢量对瞬时功率的影响不确定，“∅”表示不存在。

表1　参考电压处于第一扇区时不同η 值情况下，各矢量对瞬时功率的影响Tab.1 Influence of each vector on instantaneous power with different η in sector 1

（续）

表2　参考电压处于第一扇区时，各矢量对瞬时功率的影响Tab.2 Influence of each vector on instantaneous power in sector 1

表3　三电平NPC整流器DPC策略矢量选择表Tab.3 Vector selection table of DPC strategy used in three-level NPC rectifier

表 3中，Sp、Sq表示给定功率与实际瞬时功率比较后得到的开关信号；Sp、Sq的计算式为

式中，Hz为瞬时功率滞环宽度。

表3为目前较为准确的三电平DPC矢量表[15]，经过本文的分析发现，表3只适用于的情况。

2.2考虑直流电压利用率的三电平DPC系统矢量选择表

(3)弹性地基中的应力及位移的作用主要发生在正交各向异性板底部的有限区域内，在水平向大于板边长1.5倍，深度大于4倍板厚的区域，冲击荷载引起的应力及位移较小。

通过2.1节的分析发现三电平NPC整流器DPC策略的传统矢量选择表只适用于的情况。当η 在其他情况下，应用上述表格在某些情况下会出现一定的失控现象，故实际中需要对以上的表格进行调整。由图 4可知，η 的实际范围为对η 的范围讨论如下。

（2）当η∈(0,1/2)时，电压合矢量位于6个小矢量构成正六边形的内切圆中，系统直流电压利用率过低，本文不予考虑此种情况。

表4　三电平NPC整流器DPC策略矢量选择表Tab.4 Vector selection table of DPC strategy used in three-level NPC rectifier

仍然以VM1为例，求解选择VM1对瞬时有功功率不变的情况，有

将η 值的表达式与中矢量的长度代入式（13），解得

根据式（14），可以得到在第一扇区中，VM1对瞬时功率的影响如下

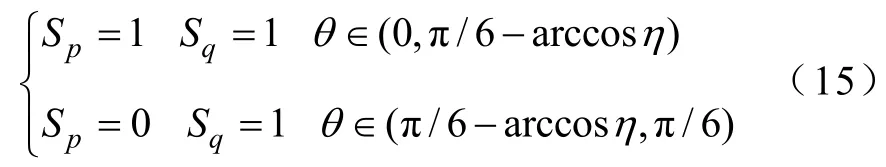
2.3三电平NPC整流器DPC策略中直流电容电压的平衡控制

三电平NPC整流器存在两个直流电容，这两个电容的电压均衡问题也就成为三电平 NPC整流器控制的一个关键问题[19]。在三电平 NPC整流器的DPC策略中，矢量选择表给出的是满足功率变化需要的矢量，而不是直接的开关状态。在图3b中，小矢量和中矢量会对直流电容电压的均衡产生影响。而每个小矢量对应两个开关状态，故可以通过合理选择小矢量的开关状态来平衡中性点电压。

由图1可以得到中性点电流io的表达式为

据此，可以定义

根据式（17）、表3和表4，当选择表3和表4中的小矢量时，根据中性点电流方向合理选择小矢量对应的开关状态，就可以实现直流电容电压的平衡控制，小矢量开关状态选择见表5。

表5　电容电压平衡的三电平DPC策略开关状态选择表Tab.5 Switching states selection table of three-level DPC system based on DC capacitor voltage balance

3 三电平NPC整流器瞬时无功功率的波动抑制

在实际应用本文提出的三电平DPC策略时，系统瞬时无功功率在某些时间内存在较大波动。图 6为采用表 3作为矢量选择表（η =0.8）时系统瞬时有功功率波动Δp和无功功率波动Δq，与负载电流的关系，系统设定的最大瞬时功率波动为 1%。仿真发现在相电流交点处系统瞬时无功功率存在异常波动，该波动将极大影响系统的整体性能。为了抑制该波动，本文提出了三种解决方案，并对其进行对比研究。

图6　三电平DPC系统单个工频周期仿真（η =0.8）Fig.6 Simulation results of three-level DPC strategy in single fundamental period (η =0.8)

3.1含过渡扇区的三电平DPC策略矢量选择表（DPC-TA）

本文提出的三电平 DPC策略矢量选择表共有12个扇区，在扇区之间切换时，可能存在矢量误选现象。如在1、2扇区间切换时，若合矢量位于第1扇区而误选第2扇区对应的矢量，会导致瞬时功率得不到及时调节。当DPC策略瞬时功率滞环宽度较小、系统开关频率较高时，误选对系统的影响很小，可以忽略。但当系统瞬时功率滞环宽度较大、开关频率较低时，误选矢量的作用时间变长，对系统产生影响较大。见表3所列，如果电压合矢量在第一扇区内，经过比较得到Sp=0、Sq=0（有功、无功都需减小），理论上应该选择矢量VL1，但是由于处于扇区边界，系统错误地认为电压合矢量位于第二扇区，此时系统会选择VM1对功率进行控制，此矢量的实际结果为Sp=0、Sq=1（有功减小，无功增加），使系统的无功进一步增大。

一种简单的解决方案是引入过渡扇区、输出过渡矢量来减小系统瞬时功率非正常波动。常用的过渡矢量选择方法是在过渡扇区中添加相邻两个扇区的公共矢量[20]。在三电平NPC整流器DPC策略中，存在如下两种扇区过渡情况：

（1）从偶数扇区过渡到奇数扇区。此时两个扇区的公共矢量为小矢量和大矢量。选择两个扇区的公共小矢量作为过渡矢量，除了可以减小系统的非正常瞬时波动外，还可以为下一个扇区的开关矢量选择做准备（公共小矢量距离下一个扇区的可选矢量距离较近，可避免出现多相跳变的情况）。

（2）从奇数扇区过渡到偶数扇区，此时公共矢量为中矢量，选择中矢量作为过渡矢量。

根据以上分析，可以得到一种简单的含过渡扇区的三电平DPC策略矢量选择表（简称DPC-TA），表 6中给出了时DPC-TA表的具体矢量。其中表示从奇数扇区转向偶数扇区的过渡扇区表示从偶数扇区转向奇数扇区的过渡扇区，文中设定过渡扇区对应圆心角（如图4所示）为1°，即当圆心角的范围为29.5°～30.5°时输出扇区中的对应矢量。

表6　三电平DPC策略矢量选择表（DPC-TA）Tab.6 Vector selection table of DPC strategy (DPC-TA)

3.2改进的含过渡扇区的三电平DPC策略矢量选择表（DPC-TB）

3.1节中过渡矢量的选择没有考虑其对瞬时功率的影响。仍以表3为研究对象，考虑从奇数扇区向偶数扇区过渡时矢量误选情况（以第1扇区过渡到第 2扇区为例）。由 3.1节知，如果 Sp=0、Sq=0时出现矢量误选择，将使无功功率波动变大；如果Sp=0、Sq=1时出现扇区的误选择，对瞬时功率的影响不变。继续分析其他扇区间过渡的情况，可以得到表7所列的矢量误选对系统瞬时功率影响。表7中，θ2i−1→θ2i（i=1,…,6）表示奇数扇区向偶数扇区过渡的情况，θ2i→θ2i+1（i=1,…,6）表示偶数扇区向奇数扇区过渡的情况；Δp、Δq表示在扇区过渡时，合矢量在上一个扇区而误选下一个扇区内矢量时对瞬时功率的影响，“＞0”表示瞬时功率增加，“＜0”表示瞬时功率减小；E表示矢量误选与瞬时功率理论期望变化之际的关系，“√”表示矢量误选的结果与期望相符，“×”表示误选的结果与期望不符。

表7　三电平DPC策略矢量误选对瞬时功率的影响Tab.7 Influence on instantaneous power with improper vector selection

表8　三电平DPC策略矢量选择表（DPC-TB）Tab.8 Vector selection table of DPC strategy (DPC-TB)

基于表 7，只有少数情况下矢量误选将引起瞬时功率的非正常变化，因而只需要对这些引起系统瞬时功率非正常变化的矢量误选进行修正。据此本文提出一种改进的带过渡扇区三电平 DPC系统矢量选择表（简称DPC-TB），表8给出了3/2)时 DPC-TB表的具体矢量。其中， θi′和 θi′（i=1,…,6）分别表示从奇数扇区转向偶数扇区和从偶数扇区转向奇数扇区的过渡扇区，设定过渡扇区对应圆心角为1°。

3.3考虑瞬时功率耦合项的三电平DPC策略矢量选择表（DPC-TC）

3.1节和3.2节着重分析了扇区过渡时矢量误选对系统瞬时功率的影响。实际中，还有一个很重要、会影响瞬时功率波动的量——瞬时功率的耦合项。一般认为，DPC策略的理论基础为式（8），该式中为了分析方便忽略了瞬时功率的耦合项，若系统额定无功功率为0，式（7）可以简化为

实际中，Ls为交流侧电感，其感抗值因存在理论下限而不可能无限小[2]，因而耦合项ωLsp对系统瞬时无功功率的影响不可能忽略不计。

以图6为例，图6是在三相参考电压满足式（18）时得到的，考虑瞬时无功功率第一个波动较大的区域（θ ≈30°）。图7为瞬时无功功率波动较大区域矢量在dq轴的投影情况，此时参考电压矢量处于第10和第11两个扇区（见表3）的相邻阴影区域。由图6可知，系统瞬时无功大于给定值，瞬时有功在给定值附近波动，所以Sq=0，Sp=1或0。由表3可知，在Sp=1、Sq=0时，输出矢量为VS6；在Sp=0、Sq=0时，输出矢量为VL6。由图7可知，VS6和VL6在q轴上的投影为负，根据式（8），系统瞬时无功功率将逐渐减小，但由图6可知瞬时无功功率的波动先变大后变小，与理论分析（式（8））不符。若考虑含有耦合项的式（18），图6的情况就很容易解释了。在式（18）中，q轴上存在耦合项ωLsp（始终为正），当3Uurq＞ωLsp时，3Uurq+ωLsp始终为正，无功功率持续增加，直至3Uurq＜−ωLsp后瞬时无功功率才逐渐变小。

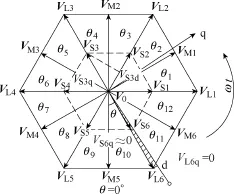
图7　瞬时无功功率波动较大区域矢量在dq轴上的投影（θ ≈30°）Fig.7 The projection of each vector in dq axes with large reactive power fluctuation (θ≈30°)

由图7和式（18）可知由偶数扇区向奇数扇区过渡时，由于耦合项的存在，表3中矢量对无功功率的控制效果都很差。一个工频周期内出现6次偶数扇区向奇数扇区的过渡，因而无功功率有6次大的波动。借鉴3.1节和3.2节中加入过渡扇区的方法及 2.2节中矢量的选择方法，本文提出一种考虑瞬时功率耦合项的三电平DPC策略矢量选择表（简称DPC-TC），表9中给出了η∈(1/3,3/2)时的DPCTC。其中和分别表示从奇数扇区转向偶数扇区和从偶数扇区转向奇数扇区的过渡扇区对应圆心角仍为1°，对应圆心角需求解得到。

表9　三电平DPC策略矢量选择表（DPC-TC）Tab.9 Vector selection table of DPC strategy (DPC-TC)

考虑ϕ 极限情况，即小矢量可对无功功率有效调节

式中，ϕ 为过渡区域的宽度，其最小值为

4 仿真和实验

为了验证本文所提方法的正确性，搭建了三电平 NPC整流器仿真和实验平台，功率器件选择BSM50GB60DLC型 IGBT，钳位二极管选择MEE75—12DA型二极管。系统主电路如图1所示，控制框图如图3所示，仿真实验平台的关键参数见表10。

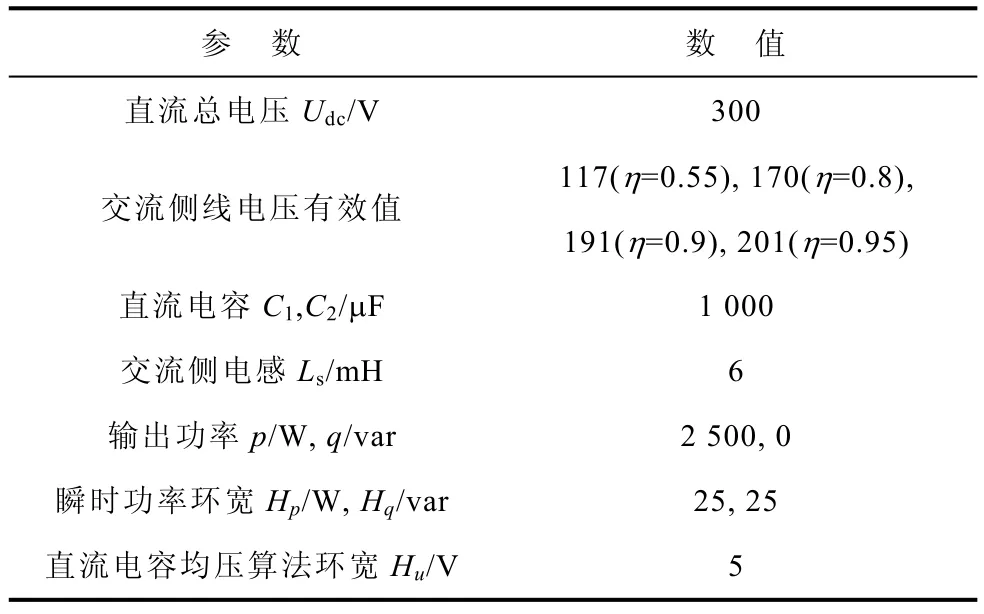
表10　三电平NPC整流器DPC系统仿真实验平台参数Tab.10 Key parameters of simulation and experiment platform of three-level DPC system

图8为理想情况下采用不同矢量选择表三电平DPC策略的仿真结果。初始时刻给定有功功率为1 250W，无功功率为0var，在0.1s末有功功率跳变为2 500W。三电平NPC整流器瞬时功率p和q、直流电容电压 uC1和 uC2、输出电压脉冲 Uab和 Uc及网侧电压ua和电流ia的波形在图8中给出。表11和表 12为仿真结果中各项重要指标对比。由图 8可知，当η∈(1/3,3/2)时，应用表3中各矢量时系统的瞬时有功功率的控制效果较好；系统瞬时无功功率在绝大多数情况下控制效果较好，少数时间内存在波动。而当η∈(1/2,1/3)，应用表3中各矢量时系统的瞬时功率存在很大的误差，而采用表 4作为矢量选择表后，系统的瞬时功率控制效果很好。进一步观察发现，图8f中各相开关状态增加，因而应用表4为矢量选择表时会增加系统开关损耗。

图8　三电平NPC整流器DPC策略仿真结果Fig.8 Simulation results of DPC system in three-level NPC rectifier

表11　三电平DPC策略仿真结果对比（p=1 250W，q=0var）Tab.11 Comparisons of simulation results of three-level DPC system (p=1 250W, q=0var)

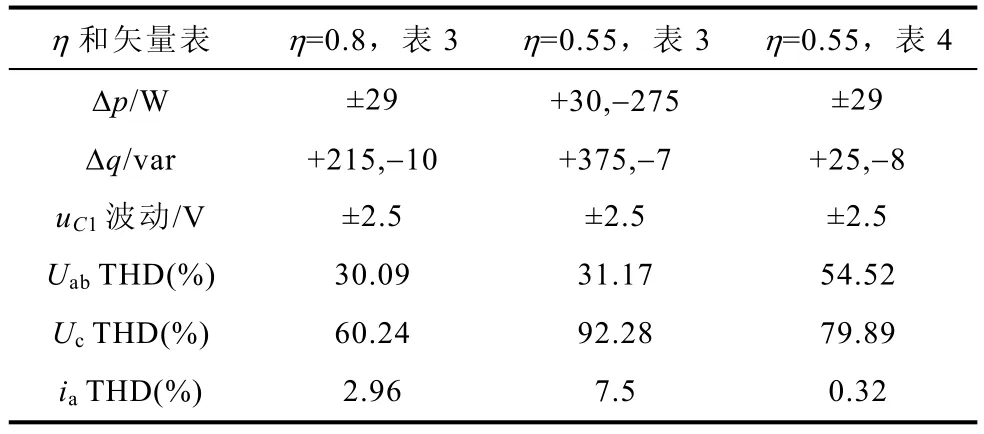
表12　三电平DPC策略仿真结果对比（p=2 500W，q=0var）Tab.12 Comparisons of simulation results of three-level DPC system (p=2 500W, q=0var)

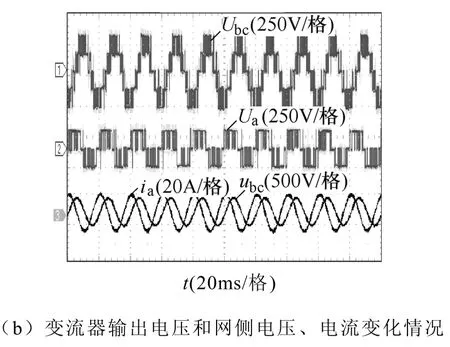
图9　三电平整流器DPC策略实验结果(η =0.8, 表3)Fig.9 Experiment results of DPC system in three-level NPC rectifier (η =0.8, Tab.3)

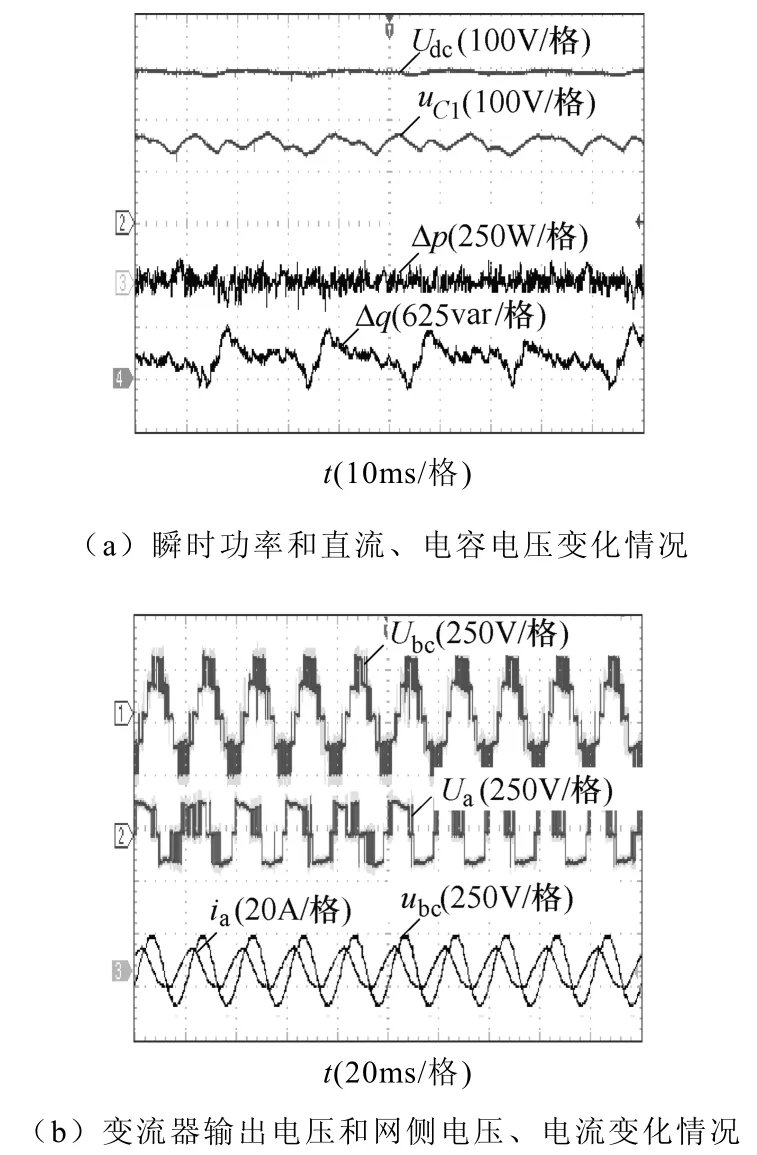
图10　三电平整流器DPC策略实验结果（η =0.55, 表3）Fig.10 Experiment results of DPC system in three-level NPC rectifier (η =0.55, Tab.3)

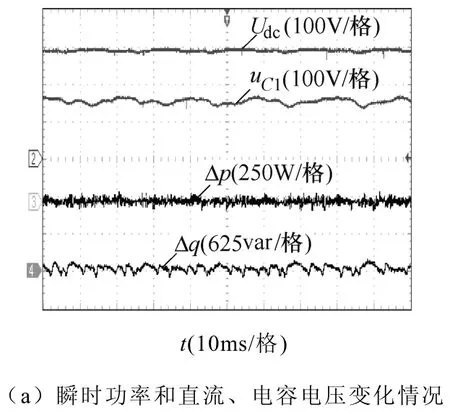
图9～图11为采用不同矢量选择表时三电平DPC策略的实验结果，设定系统输出有功功率为2 500W，无功功率为0var。图中给出了三电平NPC整流器瞬时有功功率变化量Δp和瞬时无功功率变化量Δq、直流总电压Udc和电容电压uC1、变流器输出线电压脉冲 Ubc和 Ua及网侧线电压 ubc和电流 ia的波形，表13为实验结果对比。实际系统受采样准确度、器件散热工艺和驱动电路功率等多方面因素的影响，其器件平均开关频率较低，因而实验结果与仿真结果在定量比较方面有一定差异。由图 9～图11及表13可知，仿真结果和实验结果从性质上完全相符。通过理论分析、仿真和实验表明表 3适于应用在η∈(1/3,3/2)范围，当直流电压利用率较低（η∈(1/2,1/3)）时，采用本文提出的表4作为矢量选择表则可以避免系统瞬时功率的异常波动。

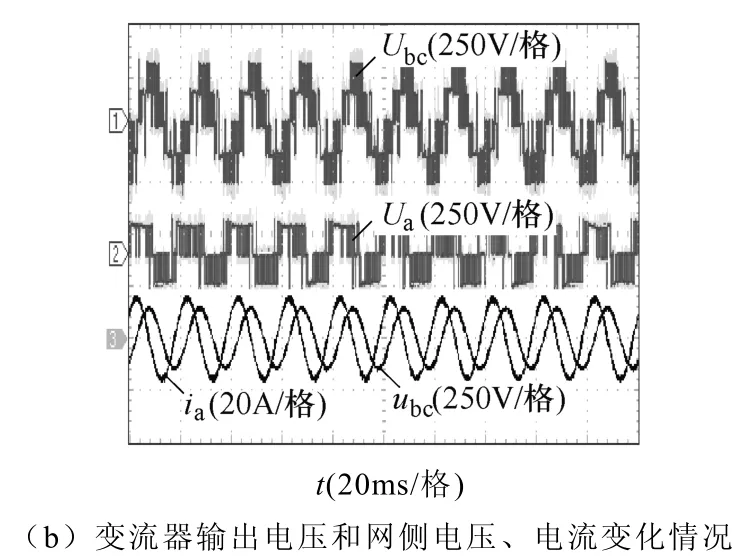
图11　三电平整流器DPC策略实验结果（η =0.55, 表4）Fig.11 Experiment results of DPC system in three-level NPC rectifier (η =0.55, Tab.4)

表13　三电平DPC策略实验结果对比（p=2 500W，q=0var）Tab.13 Comparisons of experiment results of three-level DPC system (p=2 500W, q=0var)

图 12为η =0.8时分别应用本文提出的三种抑制瞬时功率波动的矢量选择表时三电平 DPC系统的仿真结果，表14给出了三种情况时系统的仿真结果对比。通过图12和表14，并对比之前的仿真结果（η =0.8，表3），应用表6会增大系统瞬时功率波动，也增加输出相电压和线电压脉冲的THD，最终导致负载电流THD增大，因而传统的过渡扇区添加方法（表 6）无法减小瞬时无功功率异常波动。应用表8时，系统瞬时有功功率波动基本不变，输出相电压和线电压脉冲的THD增加，系统瞬时无功功率波动略有减小，由此可证明系统瞬时无功功率的异常波动并非主要由扇区过渡过程中矢量的误选造成。应用表9时，系统瞬时有功功率波动基本不变，输出相电压和线电压脉冲的THD增加，系统瞬时无功功率波动得到很好的抑制，负载电流 THD大幅减小，由此可证明三电平系统瞬时无功功率异常波动的主要原因是忽略了瞬时功率耦合项。

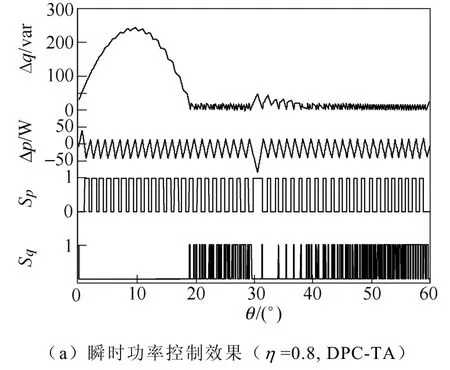
表14　三电平DPC策略瞬时无功控制仿真结果对比（p=2 500W，q=0var）Tab.14 Comparisons of simulation results of three-level DPC system (p=2 500W, q=0var)

图13～图15分别为采用DPC-TA、DPC-TB和DPC-TC三种矢量选择表时三电平DPC策略的实验结果，设定系统有功功率为 2 500W，无功功率为

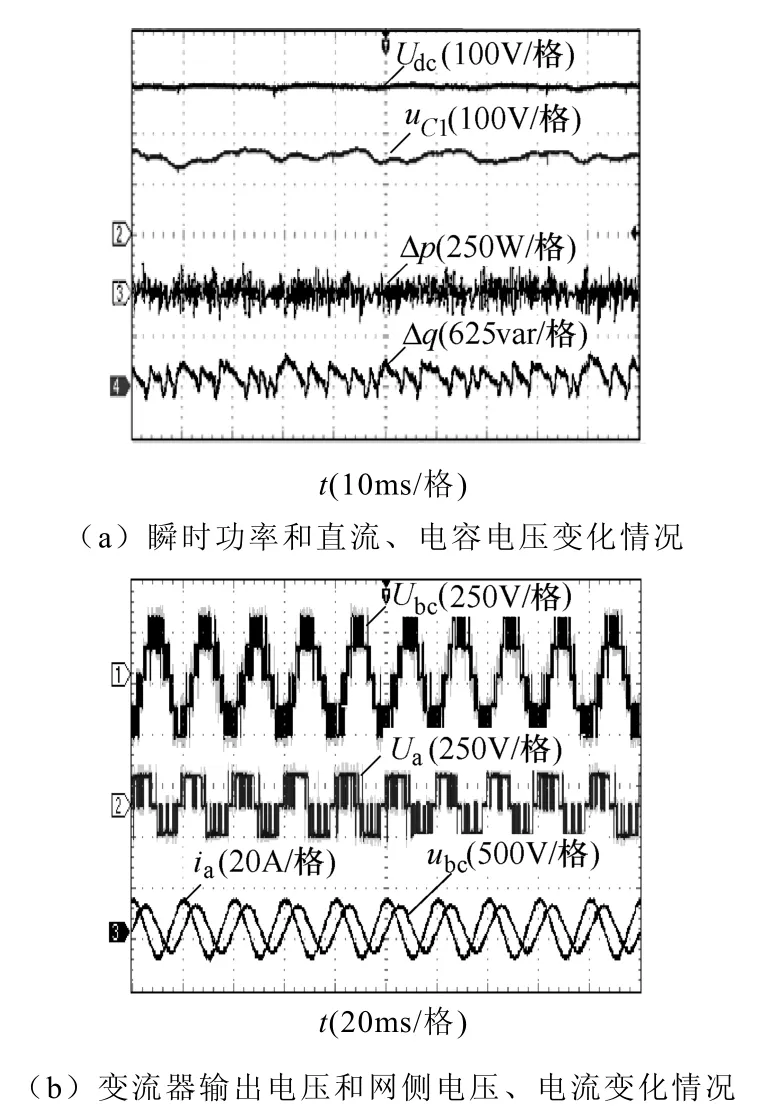
图13　三电平整流器DPC策略实验结果（η =0.8，表6）Fig.13 Simulation results of DPC system in three-level NPC rectifier (η =0.8, Tab. 6)

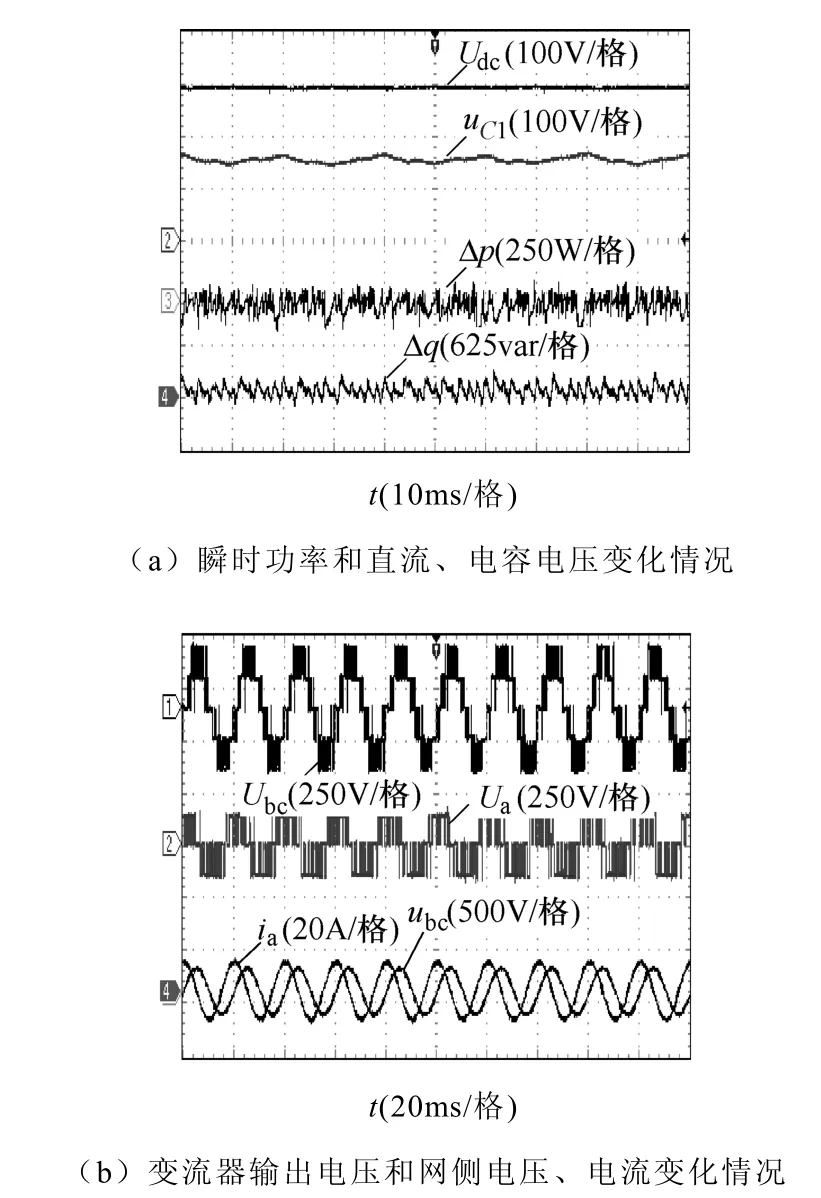
图14　三电平NPC整流器DPC策略实验结果（η =0.8，表8）Fig.14 Simulation results of DPC system in three-level NPC rectifier (η =0.8, Tab. 8)

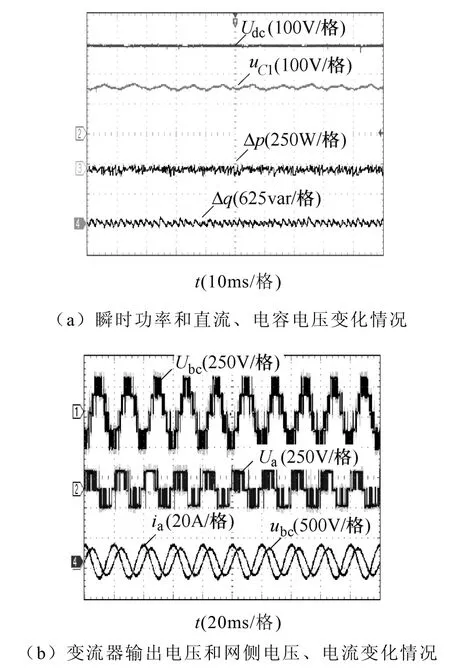
图15　三电平NPC整流器DPC策略实验结果（η =0.8，表9）Fig.15 Simulation results of DPC system in three-level NPC rectifier (η=0.8, Tab. 9)

表15　三电平DPC策略瞬时无功控制实验结果对比（p=2 500W，q=0var）Tab.15 Comparisons of instantaneous power control experiment results of three-level DPC system (p=2 500W, q=0var)

5 结论

本文分析了三电平 DPC策略的工作原理及系统瞬时功率与直流电压利用率的关系，在此基础上提出一类新颖的三电平DPC策略。该策略对系统直流电压利用率进行分区，在不同的区域采用不同的矢量选择表控制系统瞬时功率。DPC策略不仅实现简单，降低了系统硬件和软件成本，而且消除了直流电容电压不平衡的NPC拓扑固有问题，同时通过过渡扇区及其对应矢量表的插入解决了瞬时无功功率异常波动影响DPC策略控制效果的关键问题，大大增加了 NPC拓扑的应用前景与市场竞争力。当然，本文提出的DPC策略也存在一定的不足之处，如系统开关频率不固定，这为硬件电路的设计增大了难度。

[1] Nabae A, Takahashi I, Akagi H. A new neutral point clamped PWM inverter[J]. IEEE Transaction on Industry Applications, 1981, 17(5): 518-523.

[2] 张兴. PWM整流器及其控制策略的研究[D]. 合肥:合肥工业大学, 2003.

[3] Franquelo L G, Rodriguez J, Leon J I, et al. The age of multilevel converters arrives[J]. IEEE Industrial Electronics Magazine, 2008, 2(2): 28-39.

[4] Akagi H, Kanazawa Y, Nabae A. Instantaneous reactive power compensators comprising switching devices without energy storage components[J]. IEEE Transactions on Industry Application, 1984, 20(3): 625-630.

[5] Peng F Z, Lai J S. Generalized instantaneous reactive power theory for three-phase power systems[J]. IEEE Transactions on Instrumentation and Measurement, 1996, 45(1): 293-297.

[6] 刘进军, 王兆安. 瞬时无功功率与传统功率理论的统一数学描述及物理意义[J]. 电工技术学报, 1998, 13(6): 6-12. Liu Jinjun, Wang Zhaoan. Uniform mathematical description of instantaneous reactive power theory and conventional power theory and its physical meaning[J]. Transactions of China Electrotechnical Society, 1998, 13(6): 6-12.

[7] Takahashi I, Noguchi T. A new quick-response and high-efficiency control strategy of an induction motor[J]. IEEE Transactions on Industry Applications, 1986, 22(5): 820-827.

[8] Depenbrock M. Direct self-control (DSC) of inverterfed induction machine[J]. IEEE Transactions on Power Electronics, 1988, 3(4): 420-429.

[9] Ohnishi T. Three phase PWM converter/inverter by means of instantaneous active and reactive power control[C]//International Conference on Industrial Electrlnics, Control and Instrumentation, 1991, 1: 819-824.

[10] Noguchi T, Tomiki H, Kondo S, et al. Direct power control of PWM converter without power-source voltage sensors[J]. IEEE Transactions on Industry Applications, 1998, 34(3): 473-479.

[11] 杨达亮, 卢子广, 杭乃善, 等. 三相电压型PWM整流器准定频直接功率控制[J]. 中国电机工程学报, 2011, 31(27): 66-73. Yang Daliang, Lu Ziguang, Hang Naishan, et al. Novel quasi direct power control for three-phase voltage-source PWM rectifiers with a fixed switching frequency[J]. Proceedings of the CSEE, 2011, 31(27): 66-73.

[12] 李爽, 王志新, 王国强. 海上风电柔性直流输电变流器 P-DPC 控制研究[J]. 电工技术学报, 2013, 28(2): 264-269. Li Shuang, Wang Zhixin, Wang Guoqiang. Predictive direct power control strategy for offshore wind power VSC-HVDC converter[J]. Transactions of China Electrotechnical Society, 2013, 28(2): 264-269.

[13] 韩愚拙, 林明耀, 郝立, 等. 电压型PWM整流器三状态直接功率控制策略[J]. 电工技术学报, 2013, 28(5): 208-211. Han Yuzhuo, Lin Mingyao, Hao Li, et al. Triple-state direct power control strategy of three phase boost type PWM rectifiers[J]. Transactions of China Electrotechnical Society, 2013, 28(5): 208-211.

[14] 张永昌, 谢伟, 李正熙. PWM整流器功率脉动最小化方法的研究[J]. 中国电机工程学报, 2013, 33(18): 57-64. Zhang Yongchang, Xie Wei, Li Zhengxi. Studies on power ripple minimization of PWM rectifiers[J]. Proceedings of the CSEE, 2013, 33(18): 57-64.

[15] 张颖超, 赵争鸣, 鲁挺, 等. 固定开关频率三电平PWM 整流器直接功率控制[J]. 电工技术学报, 2008, 23 (6): 72-76, 82. Zhang Yingchao, Zhao Zhengming, Lu Ting, et al.Direct power control with constant switching frequency for three-level PWM rectifier[J]. Transactions of China Electrotechnical Society, 2008, 23 (6): 72-76, 82.

[16] 鲁挺, 赵争鸣, 张颖超, 等. 采样延迟和误差对三电平PWM整流直接功率控制性能的影响及其抑制方法[J]. 电工技术学报, 2010, 25(3): 66-72. Lu Ting, Zhao Zhengming, Zhang Yingchao, et al. Effect of sampling delay and error on direct power control performance of three-level PWM rectifier and its restraining method[J]. Transactions of China Electrotechnical Society, 2010, 25(3): 66-72.

[17] 张颖超, 赵争鸣, 袁立强, 等. 三电平PWM整流器直接功率控制[J]. 电工技术学报, 2008, 23(5): 62-68. Zhang Yingchao, Zhao Zhengming, Yuan Liqiang, et al. Direct power control for three-level PWM rectifier[J]. Transactions of China Electrotechnical Society, 2008, 23(5): 62-68.

[18] 詹景君, 张颖超, 钱希森, 等. 基于优化 DPC策略的三电平 PWM 整流器[J]. 电源学报, 2013(2): 46-51. Zhan Jingjun, Zhang Yingchao, Qian Xisen, et al. Three-level PWM-rectifier based on optimized direct control strategy[J]. Journal of Power Supply, 2013(2): 46-51.

[19] Celanovic N, Boroyevich D. A comprehensive study of neutral-point voltage balancing problem in threelevel neutral-point-clamped voltage source PWM inverters[J]. IEEE Transactions on Power Electronics, 2000, 15(2): 242-249.

[20] 王久和, 李华德, 杨立永. 设置扇形边界死区的电压型PWM整流器直接功率控制[J]. 北京科技大学学报, 2005, 27(3): 380-384. Wang Jiuhe, Li Huade, Yang Liyong. Direct power control of three-phase boost-type PWM rectifiers with the dead zone of sector borders[J]. Journal of University of Science and Technology Beijing, 2005, 27(3): 380-384.

Direct Power Control Strategy Based on Novel Switching Table Applied in Three-Level Neutral Point Clamped Voltage Source Rectifier

Li Ning1,2Wang Yue1Wang Zhaoan1
（1. School of Electrical Engineering Xi’an JiaoTong University Xi’an 710049 China 2. School of Automation and Information Engineering Xi’an University of Technology Xi’an 710048 China）

Direct power control (DPC) strategy has the characteristics of simple algorithm and good dynamic performance in the control of three-level neutral point clamped (NPC) voltage source rectifier. This paper analyzes the basic principle of DPC strategy and deduces the relationship between system instantaneous power and parameters of AC and DC sides. Furthermore, the influence of system DC voltage utilization ratio on instantaneous power is analyzed. Then, a novel DPC strategy is proposed. The new strategy divides the system DC voltage utilization ratio into several regions, and uses different switching tables to control the instantaneous power in each region. Moreover, the novel strategy solves the DC capacitor voltage imbalance problem of three-level NPC rectifier based on the reasonable selection of switching states. Finally, this paper analyzes the reason that the system instantaneous reactive power has abnormal fluctuations in some regions of DC voltage utilization ratio,and solves it by adding transition sector and its corresponding switching table. Simulation and experimental results verify the correctness of the analysis.

Three-level neutral point clamped rectifier, direct power control strategy, DC voltage utilization ratio, DC capacitor voltage imbalance, instantaneous reactive power, abnormal reactive power fluctuation

TM464

李 宁 男，1983年生，博士，讲师，主要从事电力电子装置控制策略的研究。

E-mail: ningli@stu.xjtu.edu.cn

王 跃 男，1972年生，博士，教授，主要从事电力电子与电力传动方面的教学与研究工作。

E-mail: yuewang@mail.xjtu.edu.cn（通信作者）

国家高技术研究发展计划（863计划）（2012AA050206），国家自然科学基金（51277150、51307140、51507140），新世纪优秀人才支持计划，陕西省教育厅专项科研基金（15JK1508）和西安理工大学博士启动金（105-211421）资助项目。

2014-03-26 改稿日期 2014-10-23