基于Hausdorff度量的高光谱异常目标检测算法

赵春晖，尤伟，齐滨2，王玉磊

（1.哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨150001；2.哈尔滨工程大学水声工程学院，黑龙江哈尔滨150001）

基于Hausdorff度量的高光谱异常目标检测算法

赵春晖1，尤伟1，齐滨2，王玉磊1

（1.哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨150001；2.哈尔滨工程大学水声工程学院，黑龙江哈尔滨150001）

高光谱遥感异常目标检测中，目标和背景光谱信息难以精确地界定，导致目标检测性能下降。针对经典RX检测算法存在虚警概率高、计算量大、过程繁琐等缺点，将Hausdorff度量引入高光谱异常检测，利用改进的Hausdorff距离（MHD）从光谱匹配程度的角度，进行了高光谱异常目标检测，最大程度地将异常目标和背景分离。采用模拟数据和真实高光谱数据进行大量实验，检测性能大幅提升，算法的计算效率提高了60%，证明了本文算法比RX算法、因果RX算法和KRX算法检测效果好，效率高等优势，算法的低复杂度特性为硬件实现提供了良好的算法支持。

高光谱遥感；异常检测；RX算法；光谱匹配；Hausdorff度量

近年来，高光谱遥感在目标探测与识别等方面具有了广泛的应用。在目标检测中，不需要先验光谱信息的异常目标检测技术具有较强的实用性，经典的异常检测算法是源于多光谱遥感的RX算法［1-2］，RX算法最早是由Reed和Xiaoli Yu于1990年提出的，是用于在高斯背景统计特性和空间白化的条件下目标光谱信息和背景光谱信息均未知的目标检测［3］。随后Chang等在RX算法基础上对检测算子进行了改进［4］，2013年，Acito等提出了一种RX局部异常检测算子（L-RXD），提高了检测性能，Riley等联合了欧氏距离构造了新检测器［2］，有效地抑制了噪声的干扰。由于RX算法具有较大的计算量，导致了算法计算效率不高［5］。随后，Chang等在RX算法的基础上进行了进一步改进［6-8］，提出了高光谱目标因果RX算子（CRRXD）和实时检测RX算法，利用迭代思想大大加快了计算速度，提高了算法效率，但尚未从算法本身提高检测精度。为降低虚警概率，Kwon等提出了一种基于核机器学习的非线性RX改进算法（KRX）［9］，该算法充分地利用了高光谱波段之间的非线性统计特性，然而，大量非线性核函数的运算使得算法效率降低。

在模式识别中，豪斯多夫（Hausdorff）度量被广泛应用于人脸检测和图像配准［10-12］，例如，何力提出一种基于 Hausdorff距离的运动目标跟踪算法［13］，在运动物体的检测、识别和跟踪取得了较好的效果，H.Peyvandi提出了将基于Hausdorff相似度量的径向基函数神经网络应用于声呐信号的探测和分类［14］，在较低信噪比情况下获得了很好的检测效果，Manuel Grana等提出了基于Hausdorff距离的高光谱数据特征检索算法［15］，提高了传统算法的效率和准确率。

针对现有RX异常检测算法虚警概率高、计算量较大的问题，本文提出了一种基于Hausdorff度量的高光谱异常目标检测算法。异常目标检测问题是一个当前像元与背景光谱信息匹配相似度问题，由于使用了Hausdorff距离作为距离测度无需考虑两个点集中元素之间的对应关系，可以有效地降低噪声的干扰，最大程度地将异常目标和背景分离，提高目标边缘检测概率，检测性能大幅提升，同时，计算复杂度大大降低，提高了计算效率。

1　异常目标检测RX算子

1.1RX异常检测算子

设有L个波段的高光谱像元的光谱向量可表示为一个L维列向量ri=［r1i，r2i，...，rLi］T，假设已知光谱信号为s=［s1，s2，...，sL］T，令a=［a1，a2，...，aL］T为信号丰度，则二元假设检验可表示如下

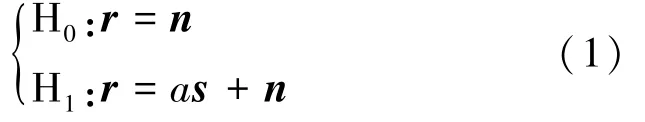
式中:H0代表目标不存在，H1代表目标存在；n是背景杂波信号，这里采用加性模型。通过广义似然比检验并经过一系列化简可以得出RX检测器，给出RX简化形式如下

其中

式中:r为L维待检测像元的光谱向量，μ为高光谱数据样本均值向量，K为高光谱数据样本协方差矩阵，η为检测阈值，N为高光谱数据中观测样本的总数。

基于相关矩阵的因果RX异常检测算子:

其中

式中:rn是当前待检测像元 （nth）的光谱特性，R（n）是采样数据的相关矩阵，该相关矩阵由当前像元之前的所有像元光谱求相关性而得，具有因果特性，因此称之为因果RX算子（CRRXD）。

1.2KRX异常检测算子

核RX（Kernel RX）是Kwon等人针对RX算子存在的问题提出的改进算法，采用非线性函数Φ将原始的高光谱遥感数据映射到高维特征空间中，得到特征空间中KRX算法可表示为

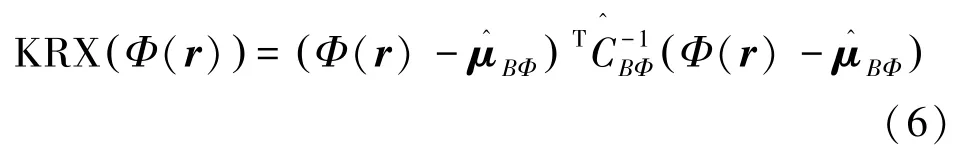
其中

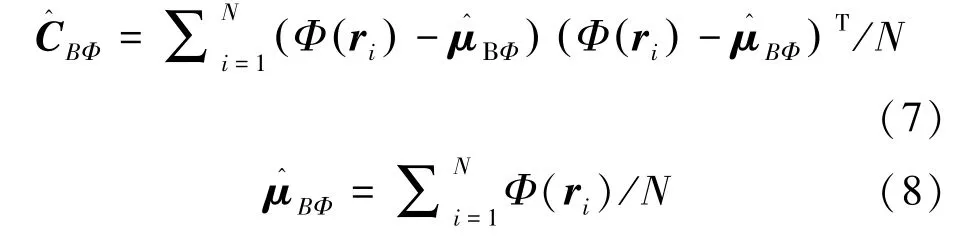
化简最终得到KRX算子的最终算子表达式:

其中:KB=K（ PB，PB）表示一个中心化的Gram矩阵，通过非中心化的Gram矩阵得到，是估计均值，KB=K（ PB，PB）为定义N×N中心化Gram核矩阵。

2　基于Hausdorff距离的异常检测算子

HD（Hausdorff distance）为在度量空间中任意两个集合之间定义的一种距离，可以用来描述两组点集之间的相似程度。

设两个点集:A=｛a1，a2，a3，...，am｝，B=｛b1，b2，b3，...，bn｝

定义Hausdorff距离为

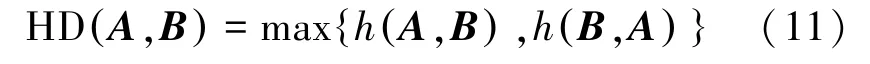
式中:h（A，B）和h（B，A）为两个点集A和B的单向距离，分别定义为

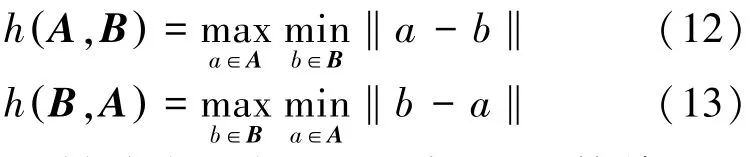
式（11）也被称为双向HD距离，是最简单的形式，‖·‖表示某种距离范数，如欧氏距离。两个单向HD距离，通常是不一样的，表示了其中一个集合中最不匹配的点到最近的另一个集合中的点的距离。应用HD距离需要证明其在集合族内部是完备度量。

定理:用κ表示Rn中全体非空紧致子集构成的集合族，即 HD:κ× κ →R，HD（ A，B）= max｛ h（A，B），h（ B，A）｝，HD是κ上一个完备度量，称作Hausdorff度量。

证明:根据度量的定义，度量需要满足三个条件，即非负性，对称性和三角不等式。非负性和对称性显然，下面证明三角不等式。设A，B，C∈κ根据紧致性，显然有HD（ A，B＜∞）设ε＞0，那么存在b∈B使得

因此，存在z∈C使得

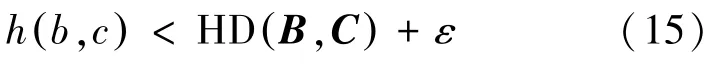
这证明A包含在C的h（A，B）+h（B，A）+2ε邻域的闭包内。类似地，C包含在A的h（A，B）+ h（B，C）+2ε邻域的闭包内。所以

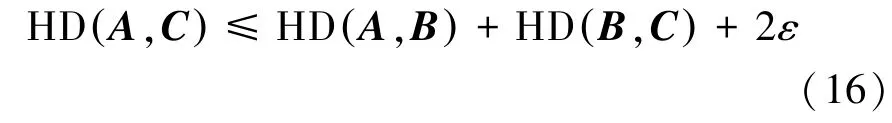
由于ε＞0的任意性，证得三角不等式性质

HD距离作为一种度量，等于两个单向HD距离的最大值，它可以解释为保证两个集合互相包含所需要的最小半径，两个集合越不相似，其互相包含的半径越大，因此，它衡量了两个点集的最大不相似程度，可以广泛应用于图像配准、目标识别和检测。

在HD距离原始定义中，它对噪声干扰的集合轮廓非常敏感，要使得两组点集之间的HD距离小，就要保证一个集合的每一个元素都需要位于另一个集合的附近。假设一个集合中存在一个或被噪声干扰的点不满足这个条件，则这两个集合的HD距离将完全取决于噪声点的位置，适应性大大降低。为提高其鲁棒性，采用改进的HD距离，表示为

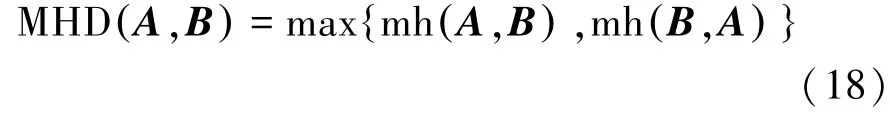
其中:

NA=m是A点集中元素的数量，改进的mh（A，B）表示为B集合中元素最小值与A中所有元素非对应欧氏距离的均值。改进的HD距离称为MHD距离，MHD距离可以有效地缓解A中噪声对距离测度的敏感程度。

RX检测算子本质是利用马氏距离进行待检测像元和背景相似度检测，引入Hausdorff距离度量解决了RX检测的灰度值图像高虚警问题，对比于KRX算法，本方法从根本上降低了计算复杂度，使得计算效率大大提高。

Hausdorff距离用于衡量两组点集之间的相似程度，在异常目标检测任务中，提取像元光谱维数据。Kwon提出了一种基于双层窗特征分解的异常检测算法。该算法利用外窗和内窗两个窗口，最大化分离背景向量和目标向量的光谱特征。其具体局部检测模型如图1所示。外层窗截取检测背景信息，而检测点位于内窗中央，内窗的其他部分认为是目标不做操作。

图1　高光谱异常目标局部检测模型Fig.1 Hyperspectral anomaly target local detection model

由于空间上同一个位置附近的背景光谱曲线差异不大，对经过双窗模型得到的背景光谱数据取均值作为平均背景光谱向量B，同时，内窗提取的像元作为待检测像元光谱向量A，对两个向量求改进的HD距离作为待检测像元的检测结果。用MHD距离来度量两个向量的相似度，两个向量的数据越相似，其MHD距离越小，两个向量的数据差别越大，其MHD距离越大，检测结果就越大，超过阈值显示检测到异常。另外，对背景光谱数据取均值作为平均背景光谱向量可以弱化MHD距离对B中噪声的敏感程度。因此，此方法可以提升原始HD距离对A和B的抗噪声性能。实际上，在高光谱异常目标检测中，相邻像元光谱数据具有相似分布特性，从原理上，应用MHD距离可以充分抑制噪声对检测结果的干扰，对两个向量进行匹配是可以对各个元素的微小差异进行积累，它会更好的检测相似度，因此，可以获得更好的检测结果。

基于MHD距离的高光谱异常检测的计算过程:

1）对于高光谱数据进行预处理，求均值做归一化。

2）设待检测像元xi，高光谱数据波段数L，利用双窗模型在排除目标像元的前提下最大化提取待检测像元附近背景W=｛xi（j）｝，i=1，2，...，N，j=1，2，...，M，N是待检测像元总数，M是待检测像元背景像元个数。

4）分别计算待检测像元到匹配背景像元和匹配背景像元到待检测像元的MHD距离:

5）比较mh（xi，xim）和mh（xim，xi）取其中的最大值作为MHD距离，将MHD距离做阈值判决输出结果。

3　实验与结果分析

为验证本文提出的MHD算法的有效性和高效性，分别用合成的模拟数据和真实的高光谱数据进行了实验。计算机的硬件配置，处理器型号为Intel Core I5，主频2.5 GHz，内存为DDR3 8 GB，仿真实验平台为MATLAB2014版本。

3.1高光谱数据描述

3.1.1模拟数据介绍

基于本文MHD算法针对异常目标检测，取用真实数据AVIRIS高光谱遥感中多种异常目标进行目标插入，该AVIRIS高光谱数据有126个波段，数据共有400×400像元。图2中圈出了四种地物的地理分布，该四种地物分别是油桶 （gasoline can，G）、房屋（house，H）、树木（tree，T）和飞机（plane，P）。合成90×90空间大小的含有126个波段的高光谱数据进行仿真实验。

该模拟数据共有4×4=16个异常点。该16个3×3大小的像元生成如下:用图2的四种物质（G，H，T，P）的光谱特性模拟四种异常目标，每行异常目标由同种物质构成。其中第一列由纯像元构成，第二列包含了75%异常像元光谱特性和25%背景光谱特性，第三列包含了50%异常像元光谱特性和50%背景光谱特性，第四列包含了25%异常像元光谱特性和75%背景光谱特性。该图可用于不同背景干扰下的多种异常目标探测。图3即为模拟数据与目标分布。

图2　四类异常目标在真实数据中的分布Fig.2 The distribution of four types of anomaly targets in real data

图3　模拟数据第100波段和目标分布Fig.3 Synthetic data 100 band image and the target distribution

3.1.2真实数据

为了验证本文提出的算法在实际应用中的有效性，采用一幅真实的高光谱数据进行仿真实验。该数据是美国圣地亚哥海军基地AVIRIS高光谱数据截取的100×100空间大小的数据。该数据有224个波段，去除水的吸收带和信噪比较低的波段后，余下的126个波段用于实验，图4即为原始高光谱的第100波段灰度显示和真实地物分布。

图4　真实数据第100波段灰度图和真实地物分布Fig.4 Real data 100 band image and the target distribution

3.2模拟数据仿真实验及分析

利用模拟数据的目的在于测试6种算法对于不同背景干扰下的多种异常目标的抗噪声性能。实验中，局部算子选择目标检测窗口设为3×3像元，背景信息提取窗口大小设为11×11像元。首先对原始高光谱数据归一化，然后根据合成数据大小和目标分布，对图2所示的合成数据分别进行全局RX算法（G-RXD）、局部RX算法（L-RXD）、全局因果RX算法（G-CRRXD）、局部因果RX算法（L-RXD）、KRX算法和本文提出的MHD算法进行检测。KRX算法中的核函数采用的是高斯径向基（RBF）核函数k（ x·xi）=exp（‖x-xi‖2/δ2），将原始数据映射到高维特征空间，通过多次仿真实验比较最终确定径向基函数的宽度δ2=100。

图5　检测结果二值图像对比Fig.5 Results of binary image contrast

对比最终检测结果的二值图像，如图5所示。图5（a）～（d）描述了采用RX检测算子在设定的阈值下得到的异常检测结果，基于马氏距离的全局RX算法检测效果很不理想，全局检测算子存在漏检目标的情况严重，图5（c）、（d）是局部算子，但由于选择的外窗的背景信息并不是完全服从正态分布，因此在16个异常目标中每一个都有不同程度的漏警，且在异常目标周围受背景干扰产生很多虚警点。图5（e）、（f）可以看出，KRX算法较RX算法检测效果好很多，没有产生漏警，只是在个别目标周围产生了虚警点，相比较而言，MHD算法效果更好，几乎没有产生漏警和虚警点，对多种异常目标的检测具有通用性。

为了量化分析本文算法的优越性，以不同算子检测的结果中的目标所占像元数量、虚警所占像元数量和计算时间作为性能指标，对上述算法进行比较分析，如表1所示。

如表1所示，由于MHD算法的计算复杂度较RX算法小很多，因此计算效率大大提高，KRX算法取得了较好的检测效果但计算时间也有所增加，而MHD算法进一步减少了计算，极大地减少了计算时间。基本达到了实时处理的要求，因此该算法更具实用性。

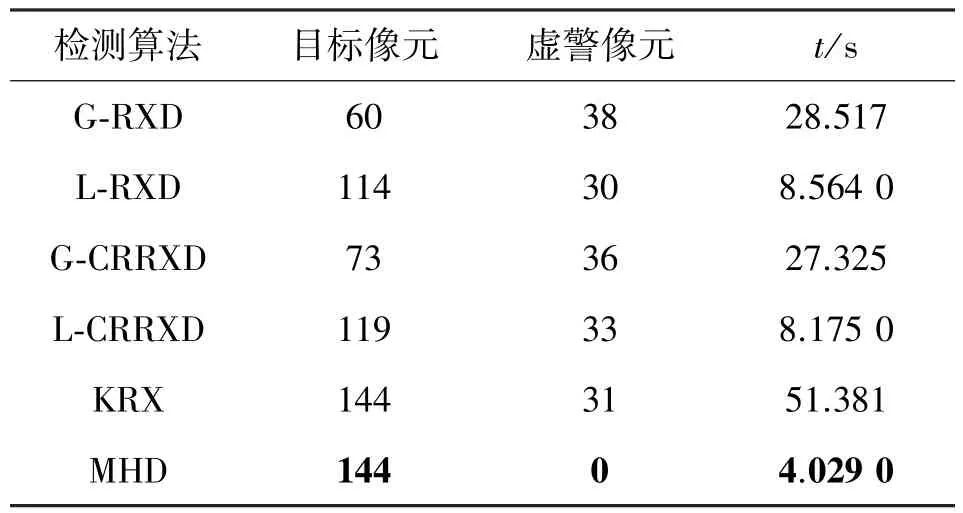
表1　不同算法性能量化分析Table 1 The quantitative analysis of different algorithms

3.3真实数据实验结果与分析

实验中，对高光谱数据去均值做归一化后，采用与模拟数据实验相同的局部窗口和核函数。为了更直观地表现HD距离用于检测的优越性，实验对比两种算法绘制出了检测灰度图像的3D峰度对比图如图6所示。其中XY轴二维平面上的点代表像元在灰度图中位置，图中蓝色到红色对应的为灰度依次由小到大，三维Z轴纵坐标表示对应像元灰度值的强弱（即峰度），由图中的峰度对比得出结论，和KRX算法相比，采用本文的MHD算法的检测结果能够产生较低的漏警概率，更容易的选择最佳阈值进行目标和背景的分离。

图6较直观地表现了传统RX、KRX和MHD算法对圣地亚哥海军基地数据飞机场的检测结果，其中RX算法检测效果不理想，由于背景光谱信息的混扰在检测到的目标附近产生较多虚警目标，KRX算法由于加入了非线性核函数，效果有所改善，但在少量目标附近仍不能区分目标和背景，采用的MHD算法是从光谱匹配程度的角度出发，检测目标和背景光谱信息差异，并将这种差异作为不相似度量，将不相似度超过阈值判断为目标，否则为判断为背景。

ROC曲线又称为接收机工作特性曲线，是一种表述检测概率Pd与虚警概率Pf之间变化关系的曲线，是检测性能定量分析中常用的手段。

图6　六种算法不同检测效果对比Fig.6 Kurtosis of MHD compared with other method

图7给出了RX、KRX和MHD三种算法的ROC曲线，一般要求虚警概率不能大于10%，从图中可以看出，在相同的虚警概率下，MHD的检测概率要远远高于RX和KRX算法，从而可知MHD算法性能远远优于其他两种算法。

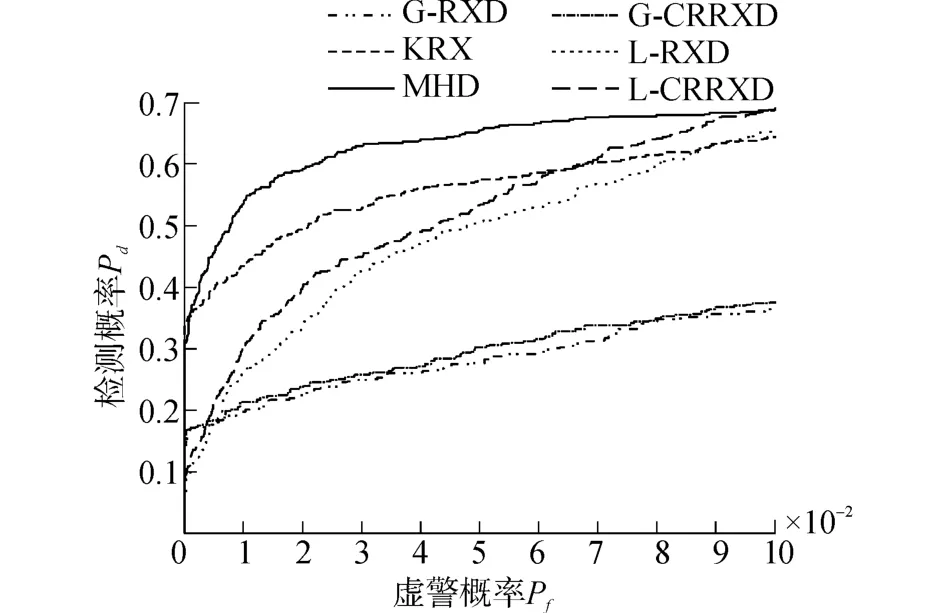
图7　ROC曲线对比Fig.7 ROC curves contrast

与模拟数据实验相同，为了量化分析本文算法的优越性，与表1对比，增加了目标个数虚警个数作为性能指标对上述算法进行比较分析，如表2所示。

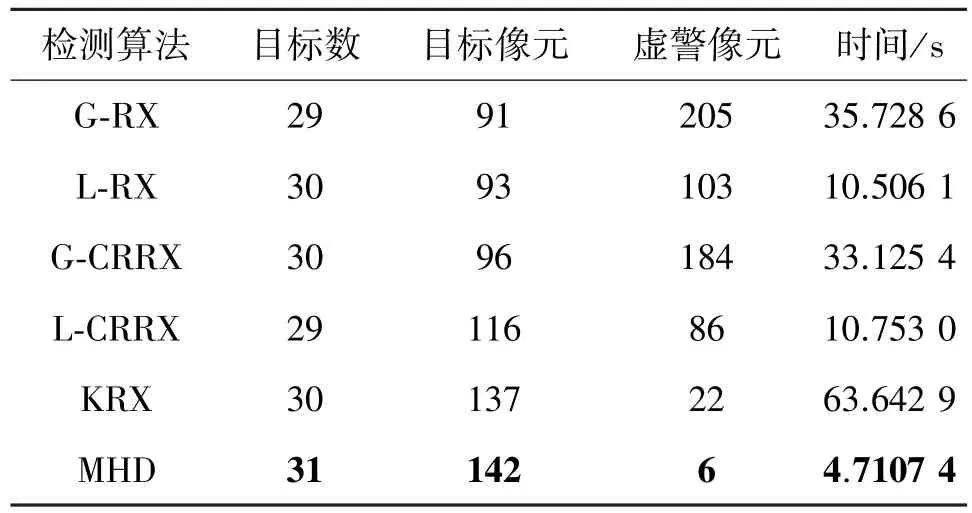
表2　不同算法性能量化分析Table 2 The quantitative analysis of different algorithms （Real data）

由表2可以看出，与其他检测算法相比，MHD算法在提升检测性能的同时极大地减少了计算时间，这是因为，在RX和KRX中存在着矩阵求逆运算和复杂的矩阵操作导致耗时较长，而在MHD中仅仅需要集合运算，这大大降低了计算复杂度，节省了计算时间，可以大量应用到具有较低计算能力的硬件实现中，例如FPGA、ARM、DSP等。上述实验充分证明了MHD算法的有效性、通用性和实用性。

4　结论

针对现有高光谱异常检测的RX算法易受背景干扰检测性能不佳和计算复杂度高这一问题，本文将Hausdorff度量引入高光谱异常检测，利用改进的Hausdorff距离（MHD）从光谱匹配程度的角度，进行了高光谱异常目标检测，最大程度地将异常目标和背景分离，同时降低了算法的计算复杂度。实验结果表明:

1）本文提出的MHD算法可以更好地检测异常目标和背景的光谱相似度，对不同复杂背景下的多异常目标具有很好的鲁棒性；

2）算法时间显著降低，接近实时高光谱异常目标检测，较低的计算复杂度为硬件实现提供了良好的算法支持。

对于极弱小异常目标的检测还存在一些不足，下一步将针对异常窗口的选择提取背景光谱信息进行深入研究。

［1］REED I S，YU X.Adaptive multiple-band CFAR detection of an optical pattern with unknown spectral distribution［J］. IEEE transactions on acoustics，speech，and signal processing，1990，38（10）:1760-1770.

［2］RILEY R A，NEWSOM R K，ANDREWS A K.Anomaly detection in noisy hyperspectral imagery［C］//Proceedings of the SPIE 5546，Imaging Spectrometry X.United States: SPIE，2004:159-170.

［3］王立国，赵春晖.高光谱图像处理技术［M］.北京:国防工业出版社，2013:110-169. WANG Liguo，ZHAO Chunhui.Processing techniques of hyperspectral imagery［M］.Beijing:National Defend Industry Press，2013:110-169.

［4］CHANG C I，CHIANG S S.Anomaly detection and classification for hyperspectral imagery［J］.IEEE transactions on geoscience and remote sensing，2002，40（6）:1314-1325.

［5］MATTEOLI S，VERACINI T，DIANI M，et al.A locally adaptive background density estimator:an evolution for RX-based anomaly detectors［J］.IEEE geoscience and remote sensing letters，2014，11（1）:323-327.

［6］ZHAO Chunhui，WANG Yulei，QI Bin，et al.Global and local real-time anomaly detectors for hyperspectral remote sensing imagery［J］.Remote sensing，2015，7（4）:3966-3985.

［7］CHEN S Y，WANG Yulei，WU Chaocheng，et al.Real-time causal processing of anomaly detection for hyperspectral imagery［J］.IEEE transactions on aerospace and electronic systems，2014，50（2）:1511-1534.

［8］WANG Yulei，CHEN S Y，LIU Chunhong，et al.Background suppression issues in anomaly detection for hyperspectral imagery［C］//Proceedings of the SPIE 9124，Satellite Data Compression，Communications，and Processing X.United States:SPIE，2014.

［9］GOLDBERG H，KWON H，NASRABADI N M.Kernel eigenspace separation transform for subspace anomaly detection in hyperspectral imagery［J］.IEEE geoscience and remote sensing letters，2007，4（4）:581-585.

［10］王靖，朱梦宇，赵保军，等.基于小波和改进型Hausdorff距离的遥感图像配准方法［J］.电子学报，2006，34 （12）:2167-2169. WANG Jing，ZHU Mengyu，ZHAO Baojun，et al.A remote sensing image registration method based on wavelet decomposition and the improved Hausdorff distance［J］.Acta electronica sinica，2006，34（12）:2167-2169.

［11］杨清夙，游志胜，张先玉.基于豪斯多夫距离的快速多人脸检测算法［J］.电子科技大学学报，2004，33（4）: 407-409. YANG Qingsu，YOU Zhisheng，ZHANG Xianyu.Fast multi-face detection algorithm based on Hausdorff distance ［J］.Journal of university of electronic science and technology of China，2004，33（4）:407-409.

［12］YI J H，BHANU B，LI Ming.Target indexing in SAR images using scattering centers and the Hausdorff distance［J］. Pattern recognition letters，1996，17（11）:1191-1198.

［13］何力.一种基于Hausdorff距离的运动目标跟踪算法［D］.合肥:中国科学技术大学，2010. HE Li.An object tracking algorithm based on hausdorff distance［D］.Hefei:University of Science and Technology of China，2010.

［14］PEYVANDI H.Evolving radial basis function neural network with Hausdorff similarity measure for SONAR signals detection/classification［C］//Proceedings of the Oceans 2009-Europe.Bremen:IEEE，2009.

［15］GRANA M，VEGANZONES M A.An endmember-based distance for content based hyperspectral image retrieval［J］. Pattern recognition，2012，45（9）:3472-3489.

本文引用格式：

赵春晖，尤伟，齐滨，等.基于Hausdorff度量的高光谱异常目标检测算法［J］.哈尔滨工程大学学报，2016，37（7）:979-985.

ZHAO Chunhui，YOU Wei，QI Bin，et al.Hyperspectral anomaly target detection algorithm based on Hausdorff measure［J］.Journal of Harbin Engineering University，2016，37（7）:979-985.

Hyperspectral anomaly target detection algorithm based on Hausdorff measure

ZHAO Chunhui1，YOU Wei1，QI Bin2，WANG Yulei1
（1.College of Information and Communication Engineering，Harbin Engineering University，Harbin 150001，China；2.College of Underwater Acoustic Engineering，Harbin Engineering University，Harbin 150001，China）

In anomaly target detection in hyperspectral imagery，it can be difficult to accurately distinguish between the spectral information of the targets and background，which leads to a decline in target detection performance.The results of the classic RX detection algorithm have a high false alarm probability，and the process is characterized by a large amount of calculation and complexity.To address these issues，we introduce the Hausdorff metric to hyperspectral anomaly target detection，prove the usefulness of its application，and make a number of improvements to suppress noise interference.In terms of the spectral matching，we separate the targets and background to a greater degree based on the improved Hausdorff distance.Experiments were performed using both synthetic and real hyperspectral data.Moreover，the results show improved detection performance and an increase in computational efficiency of nearly 60%.These experimental results prove that this algorithm has lower computational complexity and better performance than the traditional RX algorithm，casual RX algorithm，and KRX algorithm and can better support the implementation of hardware.

hyperspectral remote sensing；anomaly target detection；RX algorithm；spectral matching；Hausdorff metric

10.11990/jheu.201506087

TN911.73

A

1006-7043（2016）07-979-08

2015-06-26.网络出版日期：2016-05-27.

国家自然科学基金项目（61571145，61405041）；黑龙江省自然科学基金项目 （ZD201216）；哈尔滨市优秀学科带头人基金项目 （RC2013XK009003）；中国博士后基金项目（2014M551221）；中央高校基础研究基金项目（HEUCF1608）.

赵春晖（1965-），男，教授，博士生导师，博士.

赵春晖，E-mail:zhaochunhui@hrbeu.edu.cn.

网络出版地址：http：//www.cnki.net/kcms/detail/23.1390.u.20160527.1446.028.html