基于回馈递推的可变翼高超声速飞行器智能非线性控制

吴雨珊，江驹，甄子洋，顾臣风

（南京航空航天大学自动化学院，江苏南京210016）

基于回馈递推的可变翼高超声速飞行器智能非线性控制

吴雨珊，江驹，甄子洋，顾臣风

（南京航空航天大学自动化学院，江苏南京210016）

针对可变翼高超声速飞行器的外环稳定跟踪控制问题，考虑可变翼对建模的影响、模型参数不确定和外界未知干扰对跟踪控制性能的影响，提出基于回馈递推的智能非线性控制策略。本文首先利用巡航段气动参数的插值数据建立精确的纵向模型；然后采用输入-输出反馈线性化方法对飞行器纵向模型进行非线性映射，并根据状态变量特性将飞行器划分为三个子系统，利用回馈递推依次求取控制信号，采用RBF神经网络对未知干扰进行逼近，保证鲁棒性能。针对回馈递推设计过程中微分膨胀的问题，加入动态面控制思想进行改进。通过仿真表明，该方法可以保证闭环系统的全局稳定，并且拥有良好的跟踪性能和鲁棒性能。

可变翼；高超声速飞行器；回馈递推；RBF神经网络；动态面；鲁棒性能；微分膨胀

当今世界科学技术的快速发展，可变翼飞行器的研究得到了越来越多国家的研究机构和学者的重视。我国关于可变翼飞行器的研究还处于起步阶段。可变翼对模型建立影响较大，高超声速飞行器是具有强非线性、耦合性和快时变性的多变量系统［1-2］。因此，可变翼高超声速飞行器的飞行控制系统设计将面临传统飞控设计中所未曾遇到的更多复杂问题。

目前有关高超声速飞行器控制方法的研究文献主要集中在非线性控制方面，文献［3］将增益预置控制应用到高超声速飞行器上，但当模型非线性特性变化剧烈时，无法保证系统的闭环性能。文献［4］实现了基于动态逆方法的高超声速飞行器高度控制，文献［5］对高度非线性、高度复杂的高超声速纵向模型设计了基于动态逆的飞行控制系统，但发现该方法不具备对参数和模型变化的鲁棒性，文献［6］利用滑模控制技术为可重复使用运载器设计出时标分离的飞行控制系统，但容易在滑模面发生抖震。

回馈递推方法因其良好的全局稳定特性成为了近年来的研究热门［7］。回馈递推方法能有效利用非线性系统本身固有的非线性特性，为解决可变翼高超声速飞行器高度非线性问题提供了全新的设计思路。然而回馈递推方法应用到可变翼高超声速飞行器飞行控制中仍存在一定局限。文献［8］通过仿真说明，当存在较大外部干扰的情况下，仅采用回馈递推设计的飞控系统呈现较差的控制性能。文献［9］提出在回馈递推设计过程中存在“微分膨胀问题”，给控制器设计带来困难。

本文在精确建立的飞行器纵向模型基础上，采用基于回馈递推的智能非线性控制策略改善控制器鲁棒性能，利用动态面控制思想改进“微分膨胀问题”，最后通过数值仿真进行了验证。

1　可变翼高超声速飞行器纵向建模

1.1非线性数学模型

本文研究的可变翼高超声速飞行器采用翼身融合布局，机体轮廓为三角形，大后掠机翼与机身采用翼身融合方式，升降舵布置在机翼后缘，机翼为可变形翼面，采用在主翼两侧伸缩小翼的方式提高升力和飞行效率。该飞行器在高超声速巡航飞行条件下的纵向运动模型描述为［10-11］

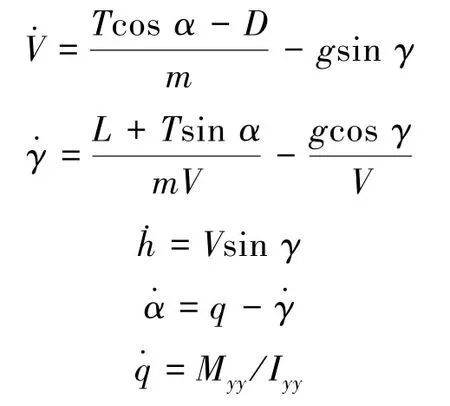
气动力和力矩表示为

可变翼对模型带来的变化主要体现在气动参数的变化上。根据高超声速飞行器巡航段气动参数的经验公式得到气动数据随着迎角变化的函数关系，再结合部分已知的小翼伸出和小翼收回的气动参数CL、CD和CM，通过插值拟合得到整个飞行包络下的气动导数。在起飞爬升段使用小翼伸出的气动导数值，以增加升力，在巡航阶段使用小翼收回的气动导数值，以减小阻力。图1以Ma=8为例给出巡航段气动参数插值拟合曲线。

图1　Ma=8时，升力系数、阻力系数、俯仰力矩系数的插值拟合曲线Fig.1 Fitting curves of CL，CD，and CMat Ma=8

发动机推力计算公式为

式中:CT为推力系数，且

发动机动态方程采用二阶系统模型:

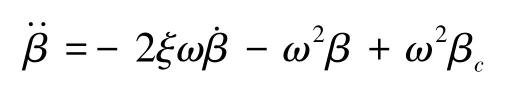
模型的控制输入为发动机节流阀调定值βc和升降舵偏转δe。

假设在高超声速巡航飞行状态下，可变翼高超声速飞行器固有参数质量m、俯仰力矩惯性积Iyy、飞机表面积s、翼弦长c存在摄动，气动参数CL、CD也存在摄动。采用所假定的额定值附加一个变化-Δ来表示参数的不确定性，即

1.2输入-输出反馈线性化

输入-输出反馈线性化是通过准确的状态变换和反馈来实现线性化。

本文所提出的基于回馈递推的可变翼高超声速飞行器控制的目的是保证飞行器的飞行速度V和飞行高度h在给定的控制输入矢量范围内能快速跟踪到指定值Vc和hc。式（2）、（3）对输出飞行速度V和飞行高度h采用全状态反馈线性化处理，即对飞行速度V和飞行高度h分别微分n和m次，直到控制输入βc或δe出现在微分式子中，于是:

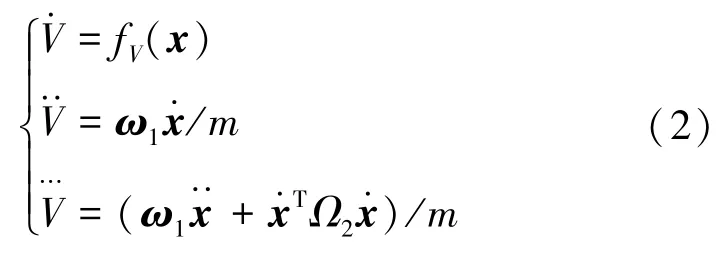
将输出飞行速度V的3次微分和飞行高度h的4次微分表示为

其中

2　基于回馈递推的智能非线性控制器设计

2.1控制器设计

在可变翼高超声速飞行器纵向建模基础上，根据式（4），受扰动可变翼高超声速飞行器纵向动力学模型可以表示为

控制器的设计目标是在系统存在未知参数摄动和外界干扰的情况下，使得可变翼高超声速飞行器能稳定跟踪给定速度参考信号和高度参考信号

假设1：假设增益矩阵G的每个元素都有界，即存在常数g1≥g0＞0，使得g0≤‖G‖≤g1。

假设2：假设期望跟踪速度和高度参考信号Vr（t）、Hr（t）连续光滑有界，且具有高阶导数并均有界。

式中:v1、v2为各子系统的虚拟控制输入。

对第一个子系统的跟踪误差向量z1=x1-yr按时间t求导得

由于x2=z2+v1，代入式（6）得

设计虚拟控制律如下

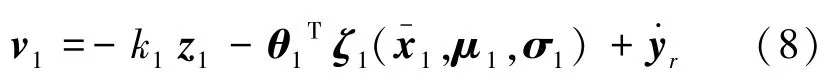
将虚拟控制律代入式（7）得

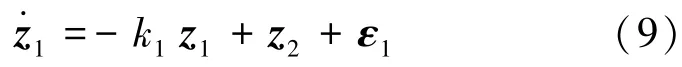
第2步:考虑闭环系统的第二个子系统:

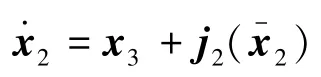
对第二个子系统的跟踪误差向量z2=x2-v1按时间t求导得

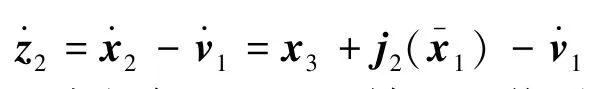
与第1步相似，用RBF神经网络对其进行逼近，并由z3=x3-v2可得:

其中

由此看出传统的回馈递推法对中间虚拟信号v1直接微分十分复杂，而动态面控制则能有效解决这类问题。将虚拟信号v1通过一阶动态滤波器得到来代替v1，为滤波器的输出，有

由上式可以求得

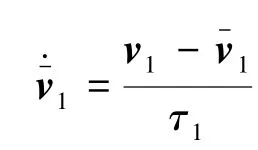
式中:τ1为滤波器的时间常数，当τ1＞0且取足够小时，可无限接近于v1。设计虚拟控制律如下

将虚拟控制律代入式（10）得

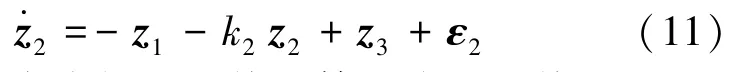
第3步:考虑闭环系统的第三个子系统:

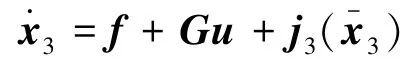
由上式可以看出，状态方程中出现了整个闭环系统的控制输入u，因此对控制输入u进行设计，对误差向量z3=x3-v2求导，并利用RBF神经网络对未知非线性函数逼近，得

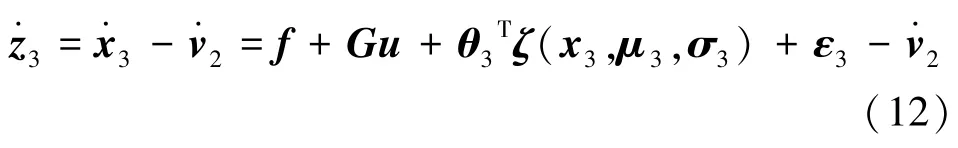
其中

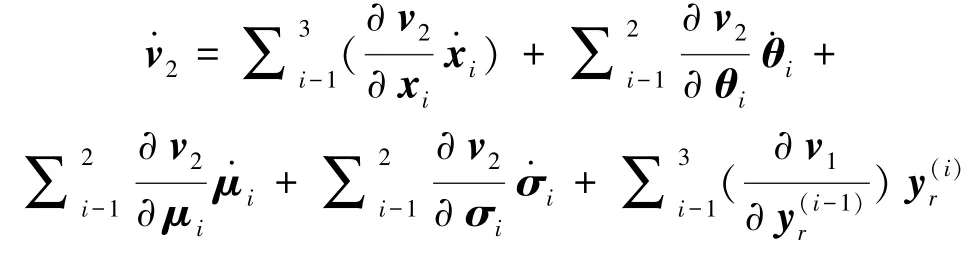
同样看出，在回馈递推法应用过程中由于需要对虚拟控制指令进行多次求导，极易造成计算膨胀，因此同样使用动态面控制解决。将虚拟信号v2通过一阶动态滤波器得到来代替v2，为滤波器的输出，有

由上式可以求得:

式中:τ2为滤波器的时间常数，τ2＞0。为了使闭环系统稳定，设计如下控制输入

代入式（12）后得

2.2稳定性分析

由控制器设计中式（9）、（11）、（13）可得

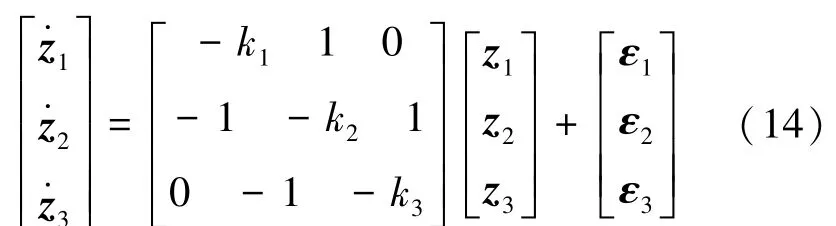
文献［8］有以下引理:考虑如下正定函数:

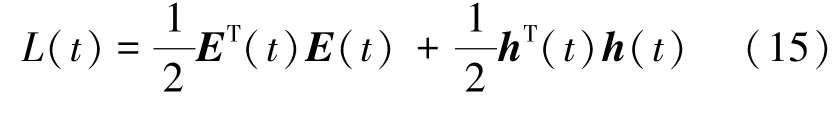
其中，δ1、δ2为大于零的常数，则给定初始紧集Ωini=｛x（0）|x（0）｝，可以得到下面结论:‖E（t）‖指数收敛于有界紧集内，其中

证明:对式（16）两边从［0，t］积分得

进一步对不等式进行缩放可得

由式（15）知ET（t）E（t）≤2L（t），则由式（17）知

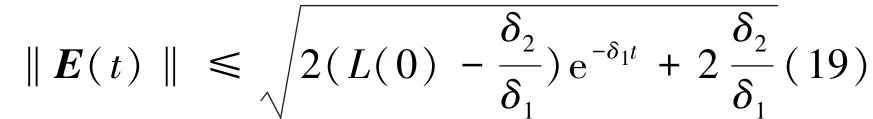
如果L（0）=δ2/δ1，则。若L（0）≠δ2/δ1，则对于任意给定的，存在TE使得当t＞TE，‖E（t）‖≤μE，令

则TE取为，当t＞TE时，‖E（t）‖≤μE，并可得到，证毕。

因此，利用李氏第二法分析其稳定性，定义闭环系统的李雅普诺夫函数为

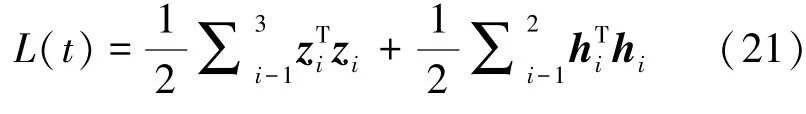
对其求导，并将式（9）、（11）、（13）代入得

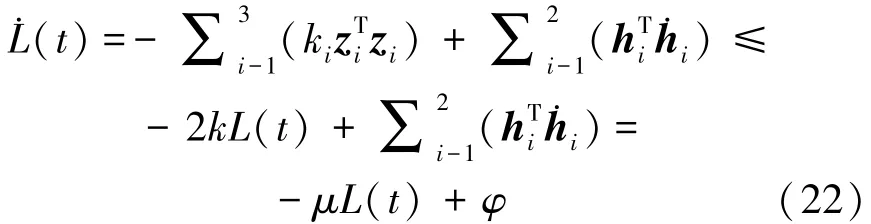
3　控制器仿真研究

针对含扰动的可变翼高超声速飞行器，为说明基于回馈递推的智能非线性控制器具有较好鲁棒特性，将其与仅采用回馈递推设计的控制器效果做比较。

3.1仅采用回馈递推控制器仿真结果

无RBF神经网络逼近系统不确定或干扰构成的未知非线性函数，选取k1=k2=k3=3，仅采用回馈递推设计控制器，当加入内部干扰:升力比标称值减少20%，阻力比标称值增加20%，外部干扰:加入10sin t的速度测量误差，其高度和速度的跟踪响应曲线如图2（a）、（b）。

图2　干扰下高度、速度跟踪曲线以及未加干扰和加入干扰下的其他量对比曲线Fig.2 Response curves of height and velocity with disturbance，and other response curves with disturbance

由图2看出，当干扰较大时，仅采用回馈递推设计的控制器不能保证良好的跟踪性能，鲁棒性较差。

3.2基于回馈递推的智能非线性控制器仿真结果

下面对基于回馈递推的智能非线性控制器进行仿真验证，选取k1=k2=k3=3，无参数摄动时高度与速度的跟踪响应如图3（a）、（b），迎角α、俯仰角速率q、航迹角γ的响应曲线如图3（c）。

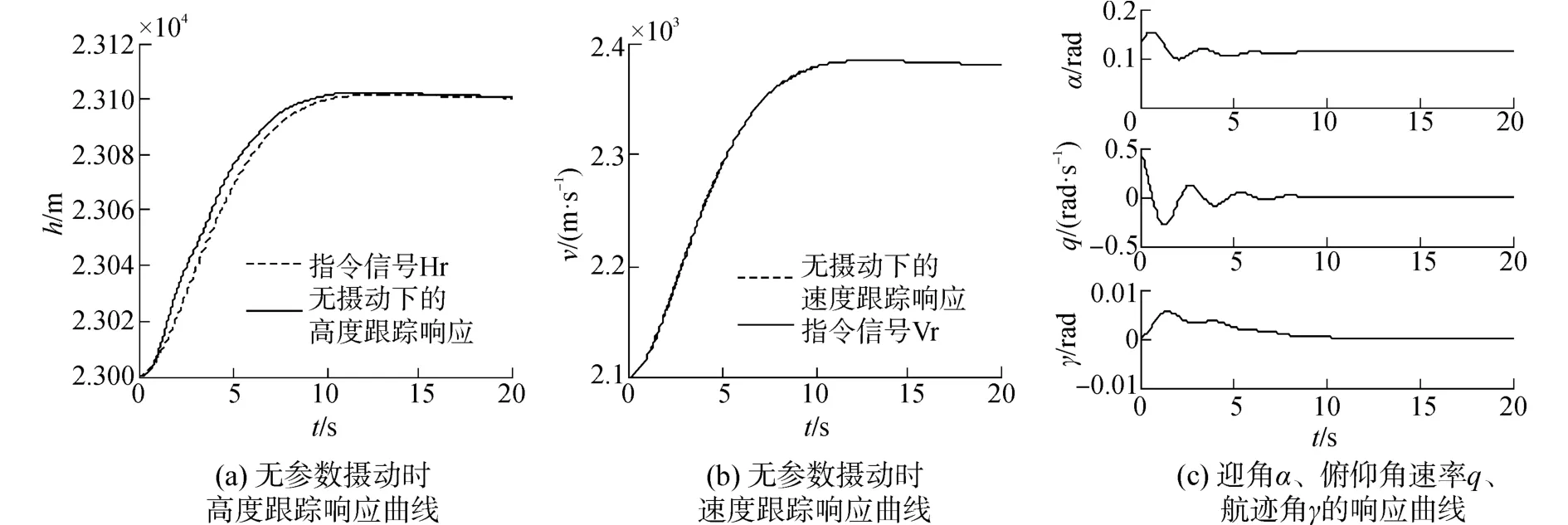
图3　无参数摄动时高度、速度、迎角α、俯仰角速率q、航迹角γ的跟踪响应曲线Fig.3 Response curves of height，velocity and α，q，γ without disturbance

当加入内部干扰:升力比标称值减少20%，阻力比标称值增加20%；外部干扰:加入10sin t的速度测量误差，基于回馈递推的智能非线性控制器高度与速度的跟踪响应如图4。由仿真结果看出，当同时存在内部干扰和外部干扰的情况下，RBF神经网络仍能有效抵消干扰对系统的影响，可变翼高超声速飞行器能快速有效的响应跟踪信号，说明基于回馈递推的智能非线性控制器拥有较好的跟踪性、鲁棒性。

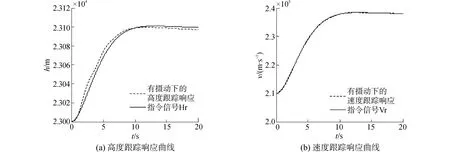
图4　干扰下的高度、速度跟踪响应曲线Fig.4 Response curves of height and velocity with disturbance

4　结论

本文设计的控制器利用回馈递推方法在处理非线性问题时的独特优越性，并采用基于梯度下降的RBF神经网络补偿回馈递推鲁棒性不足的缺点，加入动态面思想改进回馈递推“微分膨胀问题”。仿真结果表明:1）控制器能有效跟踪可变翼高超声速飞行器的外环轨迹，也实现了良好的速度跟踪，拥有良好的动态性能和稳态性能；2）控制器利用神经网络补偿飞行器在飞行过程中遇到的内部参数摄动和外部未知干扰，受一定干扰影响的情况下控制器仍拥有良好的鲁棒性能。因此本文设计的控制器具有良好的跟踪性能和鲁棒性能。

［1］黄琳，段志生，杨剑影.近空间高超声速飞行器对控制科学的挑战［J］.控制理论与应用，2011，28（10）:1496-1505. HUANG Lin，DUAN Zhisheng，YANG Jianying.Challenges of control science in near space hypersonic aircrafts［J］.Control theory&applications，2011，28（10）:1496-1505.

［2］YOUNG M，KEITH S，PANCOTTI A.An overview of advanced concepts for near-space systems:AIAA-2009-4805［R］.［S.l.］: AIAA，2009.

［3］葛东明.临近空间高超声速飞行器鲁棒变增益控制［D］.哈尔滨:哈尔滨工业大学，2011. GE Dongming.Robust gain-scheduling control of hypersonic vehicle in near space［D］.Harbin:Harbin Institute of Technology，2011.

［4］王健.基于动态逆的高超声速飞行器高度控制方法［J］.航天控制，2012，30（3）:19-22. WANG Jian.The dynamic inverse method of altitude control for hypersonic vehicle［J］.Aerospace control，2012，30（3）:19-22.

［5］BAJODAH A H.Perturbed feedback linearization of attitude dynamics［C］//Proceedings of the 2008 American Control Conference.Seattle:IEEE，2008:5222-5229.

［6］SHTESSEL Y，TOURNES C，KRUPP D.Reusable launch vehicle control in sliding modes［C］//Proceedings of the Guidance，Navigation，and Control Conference.New Orleans:AIAA，1997:335-345.

［7］LI Tieshan，YANG Yansheng，HONG Biguang.Adaptive robust dissipative designs on straight path control for underactuated ships［J］.Journal of systems engineering and electronics，2006，17（1）:177-181.

［8］周丽.基于回馈递推方法的近空间飞行器鲁棒自适应控制［D］.南京:南京航空航天大学，2009. ZHOU Li.Robust adaptive control for nearspace vehicles based on backstepping approach［D］.Nanjing:Nanjing University of Aeronautics and Astronautics，2009.

［9］张强，吴庆宪，姜长生，等.基于backstepping的近空间飞行器鲁棒自适应姿态控制［J］.南京航空航天大学学报，2013，45（5）:590-598. ZHANG Qiang，WU Qingxian，JIANG Changsheng，et al.Robust adaptive control for attitude system of near space vehicle via backstepping method［J］.Journal of Nanjing university of aeronautics&astronautics，2013，45（5）:590-598.

［10］WANG Q，STENGLE R F.Robust nonlinear control of a hypersonic aircraft［C］//Proceedings of the AIAA Guidance，Navigation and Control Conference.Reston，USA:AIAA，1999:413-423

［11］ZHU J，HUIZENGA A.A type two linearization controller for a resuable launchvehicle-asingularperturbationapproach ［C］//Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit.Providence，Rhode Island:AIAA，2004:1-16.

［12］WANG D，HUANG Jie.Neural network-based adaptive dynamic surface control for a class of uncertain nonlinear systems in strict-feedback form［J］.IEEE transactions on neural networks，2005，16（1）:195-202.

本文引用格式：

吴雨珊，江驹，甄子洋，等.基于回馈递推的可变翼高超声速飞行器智能非线性控制［J］.哈尔滨工程大学学报，2016，37（7）:963-968.

WU Yushan，JIANG Ju，ZHEN Ziyang，et al.Intelligent nonlinear control for the hypersonic morphing vehicle based on the backstepping method［J］. Journal of Harbin Engineering University，2016，37（7）:963-968.

Intelligent nonlinear control for the hypersonic morphing vehicle based on the backstepping method

WU Yushan，JIANG Ju，ZHEN Ziyang，GU Chenfeng
（College of Automation Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China）

In this paper，an intelligence nonlinear control scheme is proposed based on the backstepping method to solve the difficulty of the stable tracking control of the hypersonic morphing vehicle，considering compound disturbances as well as the influence of model uncertainties and unknown outside disturbances.First，the aerodynamic parameters of the morphing vehicle are replaced with a curve-fitted approximation in order to build an accurate hypersonic model.Then，the feedback linearization approach is used to transform the nonlinear vehicle model into a strict feedback multi-input/multi-output nonlinear system.The nonlinear system is divided into three subsystems according to the features of the state variables and the virtual control signals are calculated for every subsystem.Next，the radial basis function（RBF）is proved to have excellent capability in restraining unknown disturbances，and a dynamic surface control strategy is employed to eliminate the explosion terms.The simulation results show that the proposed method can ensure the integral stability of the closed-loop system，as well as can have excellent tracing performance and robustness.

morphing vehicle；hypersonic vehicle；backstepping；RBF neural network；dynamic surface；robustness；differential expansion

10.11990/jheu.201503009

V249

A

1006-7043（2016）07-963-06

2015-03-05.网络出版日期：2016-05-13.

国家自然科学基金项目（61304223）；教育部高等学校博士科学点专项科研基金项目（20123218120015）；南京航空航天大学研究生创新基地（实验室）开发基金项目（kfjj201420）.

吴雨珊（1990-），女，硕士研究生；江驹（1963-），男，教授，博士生导师；甄子洋（1981-），男，副教授.

吴雨珊，E-mail:wysh219959@126.com.

网络出版地址：http：//www.cnki.net/kcms/detail/23.1390.u.20160513.1344.014.html