基于非线性反馈的水翼艇纵向运动鲁棒控制
2016-10-11张显库
张显库
(大连海事大学 航海学院,辽宁 大连 116026)
基于非线性反馈的水翼艇纵向运动鲁棒控制
张显库
(大连海事大学 航海学院,辽宁 大连 116026)
为提高水翼艇纵向运动控制的鲁棒性和节能效果,在保持已有的多输入多输出(Multiple-Input Multipe-Output, MIMO)鲁棒控制器不变的基础上,引入正弦函数驱动的非线性反馈代替原有的误差线性反馈。仿真结果表明:在模型摄动时,鲁棒控制器主要改进纵摇效果,而非线性反馈控制能同时改进升沉和纵摇效果,控制效果比鲁棒控制器提升70%以上,控制能量比鲁棒控制器节省90%以上。简单的理论分析和仿真研究结果表明:正弦函数驱动的非线性反馈对于MIMO系统的控制同样适用。
水路运输; 船舶运动控制;水翼艇;非线性反馈;鲁棒控制;闭环增益成形
Abstract: In order to improve the robustness of the longitudinal motion control for hydrofoils and the energy consumption, a nonlinear sine function modulated error signal is introduced to replace the original linear error feedback while keeping the construction of the Multiple-Input Multiple-Output(MIMO) robust controller unchanged. The simulation results show that under given perturbations, the original robust controller mainly improves the pitch damping effect, in contrast, the nonlinear feedback controller decreases the heave and pitch simultaneously. Tests indicate that over 70% of control effect improvement with over 90% energy saving is achieved by introducing the nonlinear feedback.
Keywords: waterway transportation; ship motion control; hydrofoil; nonlinear feedback; robust control; closed-loop gain shaping algorithm
水翼艇控制属于多输入多输出(Multiple-Input Multiple-Output, MIMO)不稳定系统的控制且控制精度要求较高,是船舶运动控制领域中的研究热点之一。[1-4]文献[1]给出水翼艇纵向运动的多变量随机最优控制,仿真结果较为理想,但没有讨论模型摄动时的情况;文献[2]在此基础上使用闭环增益成形算法和镜像映射方法设计出水翼艇的鲁棒控制器,鲁棒性能良好。近几年,国内外相关学者[5-8]采用多种方法对水翼艇进行控制,以有效减缓船舶的纵向运动,改善乘员的晕船状况。这些研究在减缓船舶纵向运动和节能方面都还有进一步改进的空间。文献[9]提出一种正弦函数驱动的非线性反馈概念,并已在单输入单输出(Single-Input Single-Output, SISO)船舶航向保持系统的应用中取得良好的节能效果。这里在文献[2]和文献[9]的基础上将非线性反馈引入到MIMO系统中,进行有益的尝试。
1 水翼艇纵向运动数学模型
取状态向量为
(1)
式(1)中:h为水翼艇升沉位移;θ为水翼艇纵摇角。
水翼艇的纵向运动状态空间型数学模型[1-2]为
(2)
以文献[10]中的PCH水翼艇为例,其航速为48 kn,排水量为110 t,船长为35 m,船宽为9.8 m,吃水为5.2 m,所得数学模型中各系数的矩阵为
A=

(3)

(4)
若输出h和θ,则传递函数型数学模型G为
(5)
用s表示拉普拉斯算子,且有
(6)
镜像映射方法是将不稳定被控对象传递函数的不稳定零极点用对称于虚轴的稳定零极点镜像替换后形成稳定的被控对象的方法;闭环增益成形算法是利用H∞鲁棒控制理论的结果及具有工程意义的4个参数构造出闭环系统传递函数,进而反推出鲁棒控制器的算法。[3]文献[2]给出采用镜像映射和闭环增益成形算法的6阶鲁棒控制器设计为
(7)
式(7)中:c=s4+14.634 3s3+47.798 7s2+10.510 4s+33.530 4;a11=(-0.917 7s2-12.058 6s-5.285 4)/(407.262 5s4+7 042.501 9s3+35 392.983 9s2+57 838.658 1s+13 654.215 6);a12=(59.770 6s2+658.851 3s+859.778 0)/(407.262 5s4+7 042.501 9s3+35 392.983 9s2+57 838.658 1s+13 654.215 6);a21=(-5.723 4s2-30.184 6s-2.137 8)/(407.262 5s4+7 042.501 9s3+35 392.983 9s2+57 838.658 1s+13 654.215 6);a22=(-71.016s2-665.931 2s-2 235.616 4)/(407.262 5s4+7 042.501 9s3+35 392.983 9s2+57 838.658 1s+13 654.215 6)。
2 非线性反馈改进及仿真
图1为正弦函数驱动的非线性反馈结构图,图中非线性函数与常规方框图所表达的含义不同(由于没有更好的表达方法,暂时如此绘制)。设e=r-y,图1所要表达的是u=Ksin(ωe),而不是常规的结构图数学表达u=Ksin(ωe)e。u=Kr实现从手动到自动控制的飞跃;而u=Ke则实现从开环控制到闭环反馈控制的飞跃。常规闭环反馈控制为线性反馈,只将设定信号的误差直接反馈给控制器;而非线性反馈研究的是u=Kg(e),g(e)应是关于横轴反对称的奇函数。以往对于复杂系统的控制主要研究K为非线性的形式,这里保持原有K的形式不变,仅关注误差的非线性反馈形式。文献[9]给出对SISO船舶航向保持控制系统使用正弦函数驱动的非线性反馈能够节能的理论分析和仿真。这里针对MIMO水翼艇控制系统的2个通道都使用sin(0.1e)相同的非线性反馈进行仿真研究。
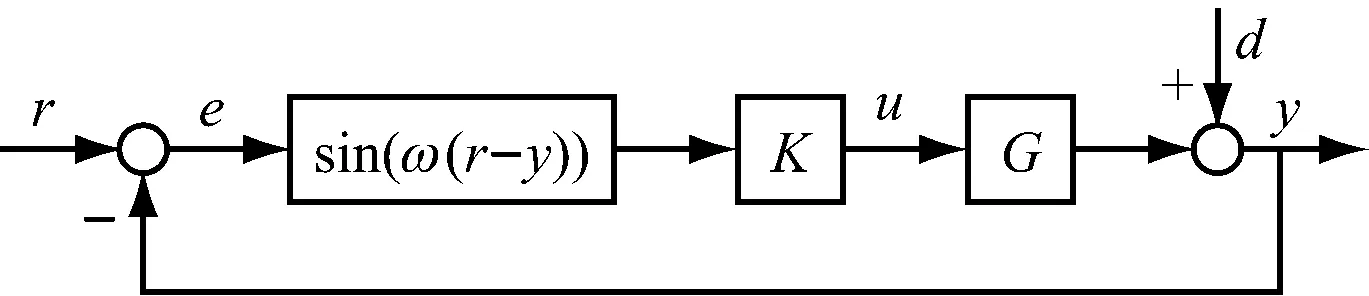
图1 正弦函数驱动的非线性反馈结构图
用MATLAB的Simulink进行系统仿真,鲁棒控制器与文献[2]相同,如式(7)所示,取T11=0.1 s,T22=4 s,唯一变化的是2个通道都使用sin(0.1e)相同的非线性反馈,仿真结果见图2。
从图2中可看出,升沉位移经非线性反馈控制后幅值明显变小,非线性反馈控制前为深色曲线(最大值为1.76 m),控制后为浅色曲线(最大值为0.29 m);纵摇角由控制前(深色曲线)的最大值13.35°降为控制后(浅色曲线)的最大值0.39°。原鲁棒控制的升沉位移最大值为1.80 m,与控制前的最大值1.76 m相比变化不大;但纵摇角由控制前的最大值13.35°降为控制后的最大值1.81°,控制效果明显。[2]
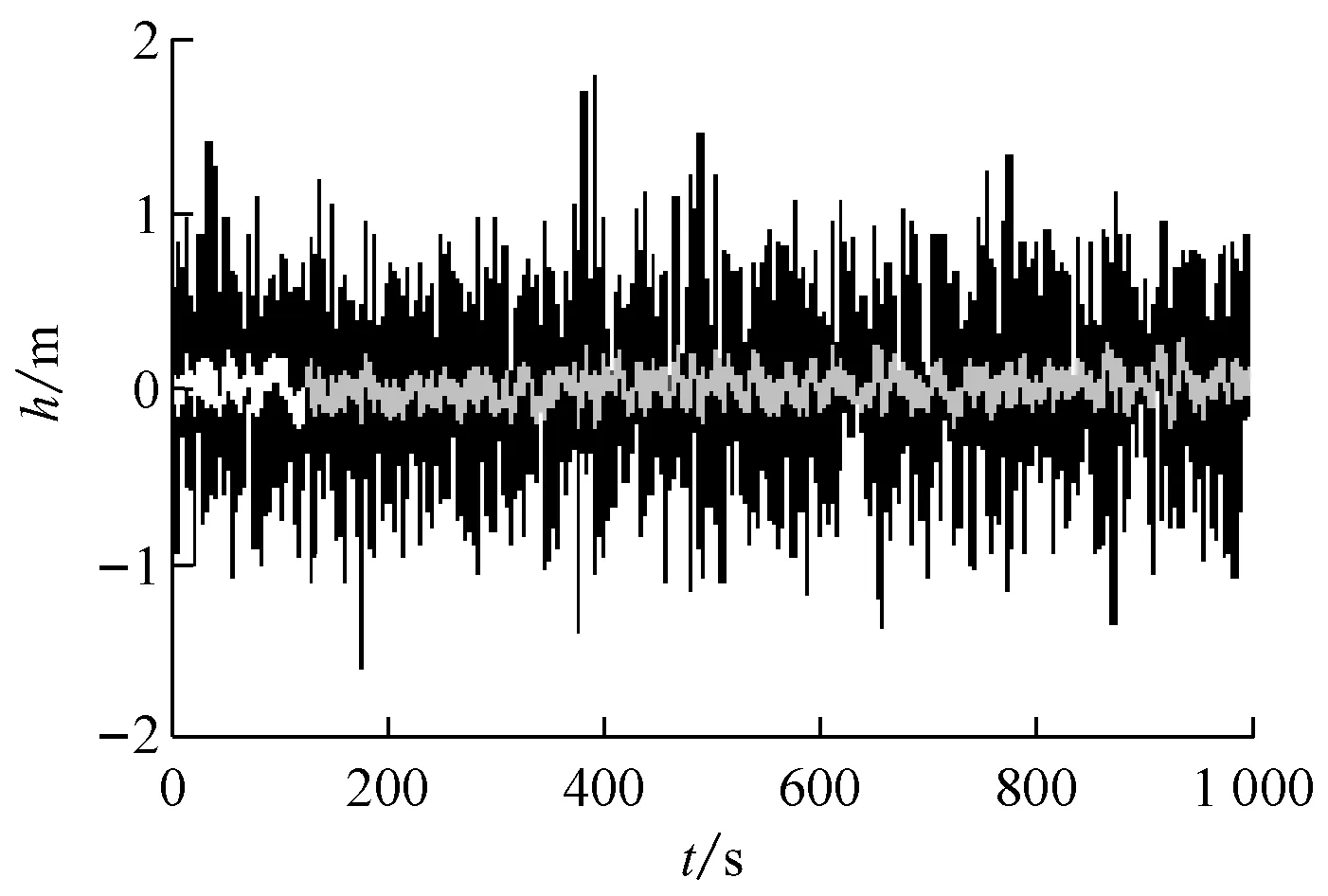
a) 升沉位移变化情况
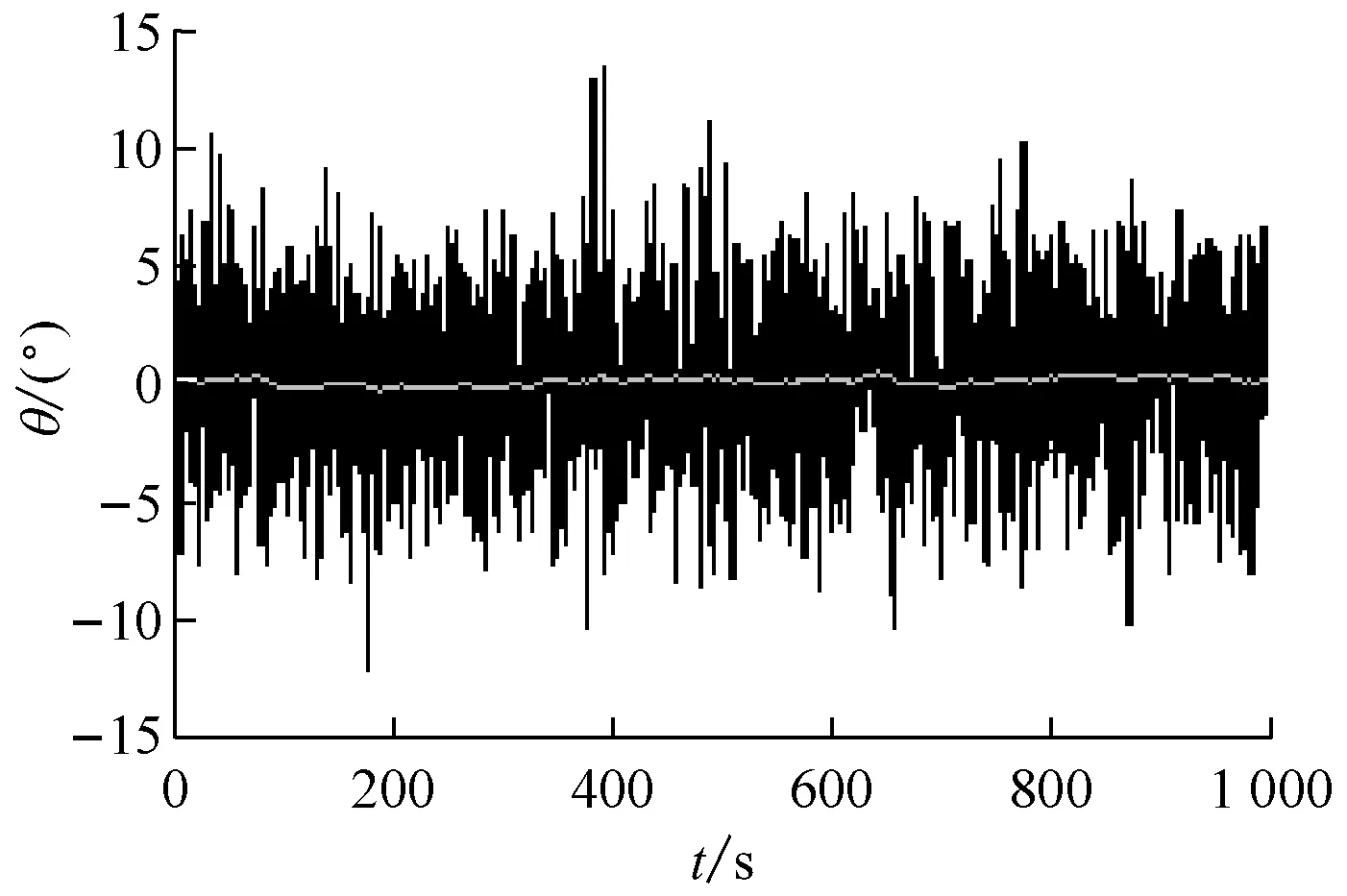
b) 纵摇角变化情况
通过比较可知:鲁棒控制器主要改进纵摇效果;而非线性反馈控制同时改进升沉和纵摇效果,升沉位移最大值降为初始最大值的16.5%,纵摇角最大值降为初始最大值的3%,分别比鲁棒控制器提升83.9%和78.4%。
图3给出模型产生摄动时的仿真结果,此时相当于在原模型上加一个0.4s的纯滞后环节e-0.4s。由仿真结果可知,升沉位移经过非线性反馈控制后幅值明显变小,非线性反馈控制前为深色曲线(最大值为1.76 m),控制后为浅色曲线(最大值为0.31 m),最大值比名义模型时稍大(增加0.02 m);纵摇角由控制前(深色曲线)的最大值13.35°降为控制后(浅色曲线)的最大值0.39°,与名义模型时相同。总体而言,摄动模型的控制效果与名义模型基本相同,说明控制器具有一定的鲁棒性。
模型摄动时,原鲁棒控制的升沉位移最大值变为4.47 m,在系统仍然稳定的前提下变化明显加剧;但纵摇角由控制前的最大值13.35°降为控制后的最大值2.20°,降低效果仍然明显。[2]
通过比较可知:模型摄动时鲁棒控制器主要改进纵摇效果(升沉位移变差);而非线性反馈控制同时改进升沉和纵摇效果,升沉位移最大值降为初始最大值的17.6%,纵摇角最大值降为初始最大值的3%,分别比鲁棒控制器提升93.1%和82.3%。
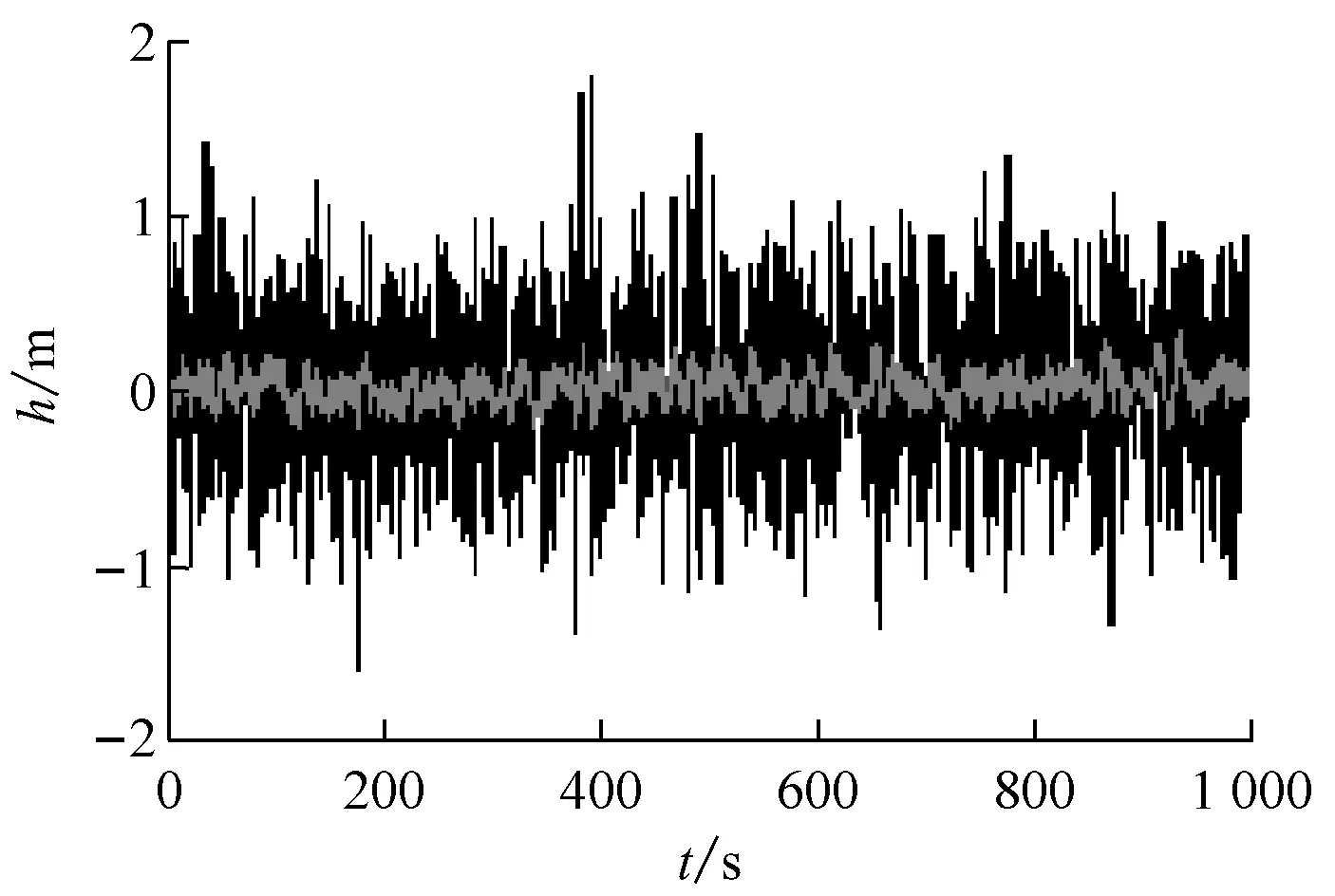
a) 升沉位移变化情况
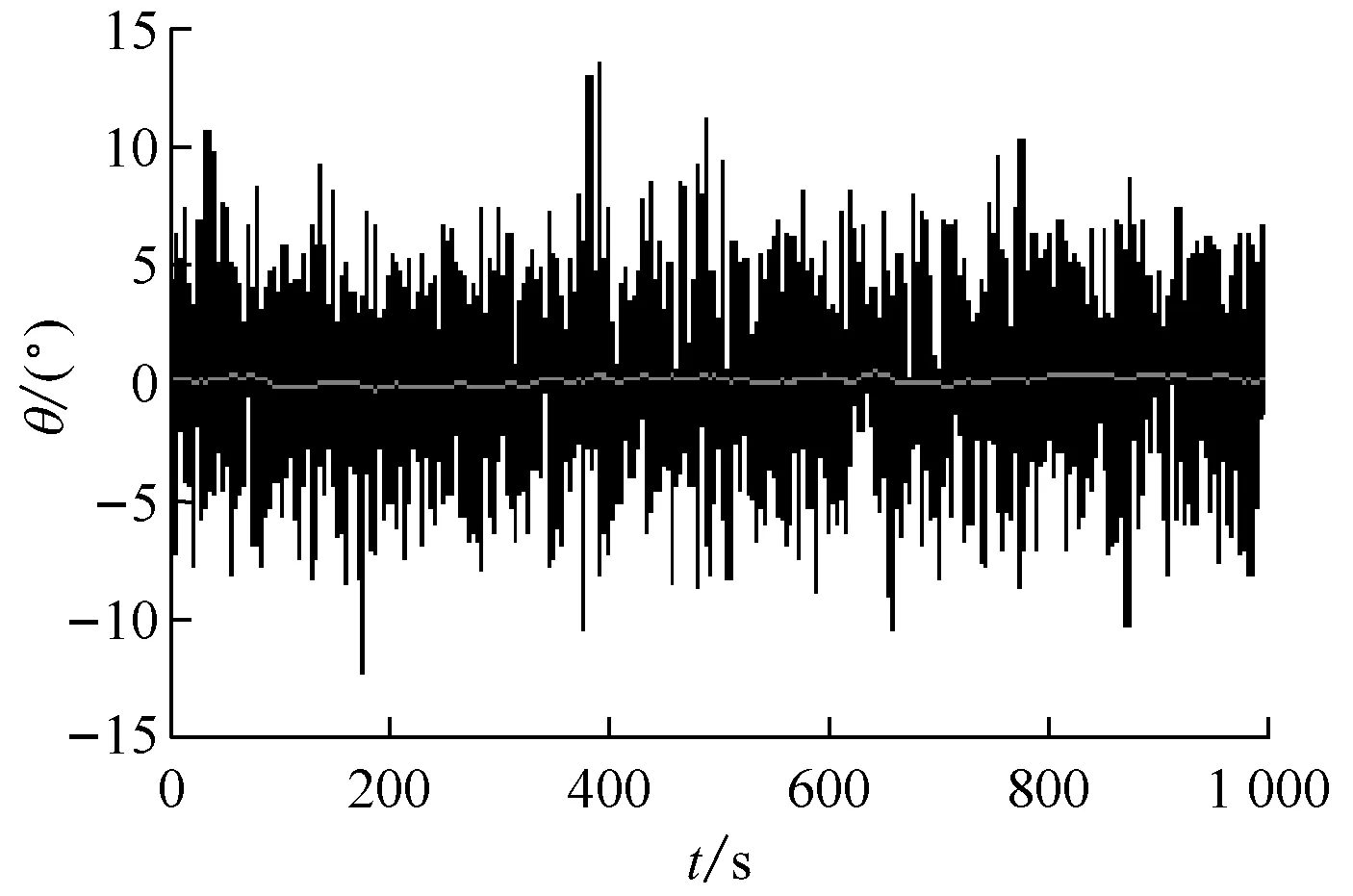
b) 纵摇角变化情况
文献[9]重点强调引入非线性反馈能够节能,针对MIMO水翼艇的控制是否具有相同效果,图4给出摄动模型时有无非线性反馈情况下2个控制通道(即δe,δf)的输出曲线。
1) 从图4a中可看出,采用鲁棒控制器时,2个控制通道输出的最大值分别为33.9°和223.1°,平均值分别为7.2°和24.9°。平均值看起来比图形中视觉观察的要小很多的原因是曲线较密,大部分数值较小的点被覆盖住了,若取5 000个大数(共19 000个数据,变步长仿真),则计算平均值是给出平均值的2.4倍,结果即与视觉观察值相近。
2) 从图4b中可看出,采用非线性反馈控制时,2个控制通道输出的最大值分别为2.5°和16.3°,与图4a相比分别降低92.6%和92.7%;平均值分别为0.45°和1.59°,与图4a相比分别降低93.7%和93.6%。
Simulink仿真中使用白噪声模拟海浪干扰,功率强度取为0.1,属于恶劣海况[3],故曲线中船舶的升沉位移和纵摇角都相对较大。
3 理论分析
对于MIMO系统,引入非线性反馈后相关理论分析较为困难,为简单起见,假设误差较小时sin(ωe)≈ωe。
3.1对系统稳态的影响
根据终值定理,可计算得到稳态误差为

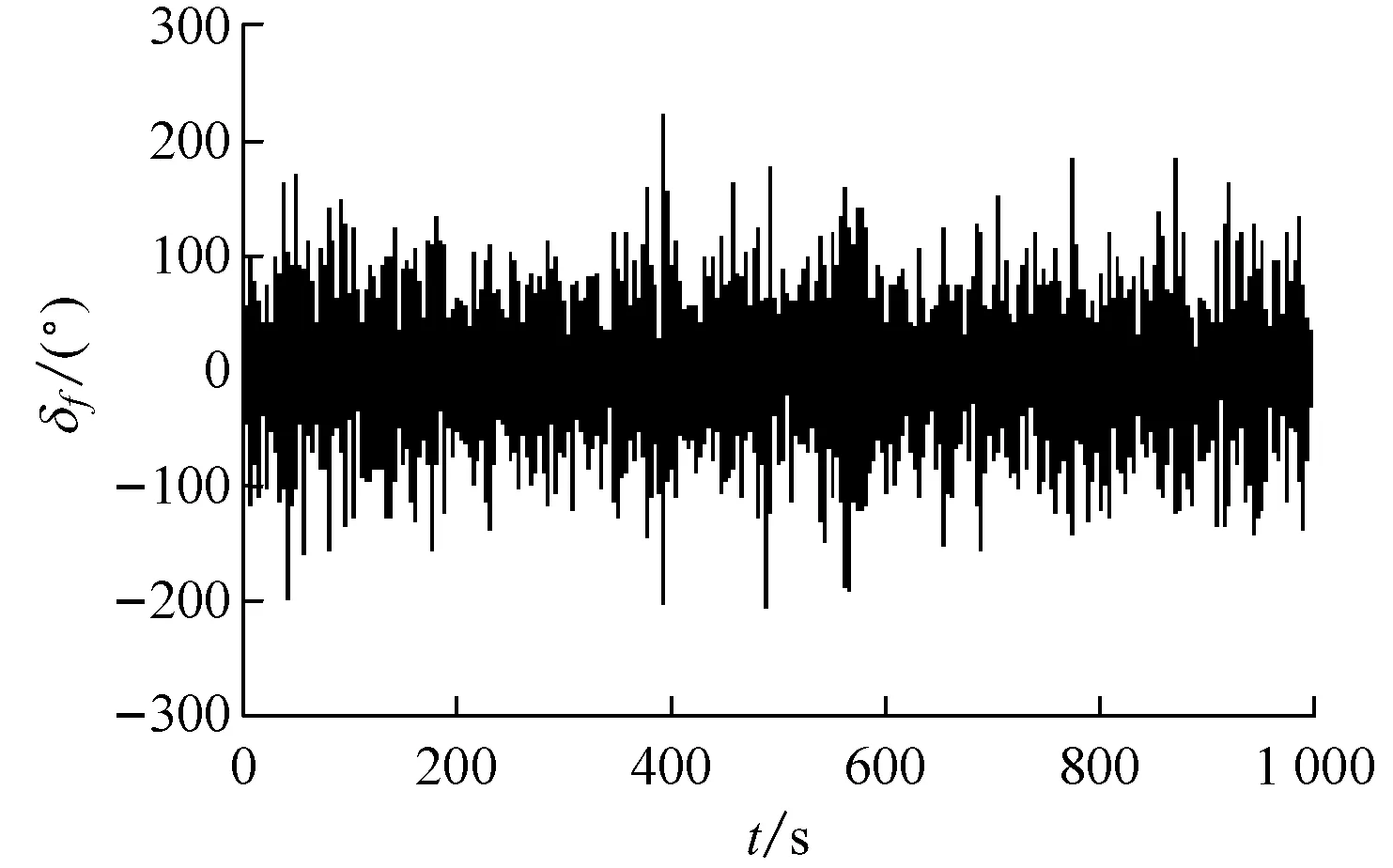
a) 鲁棒控制的控制输出
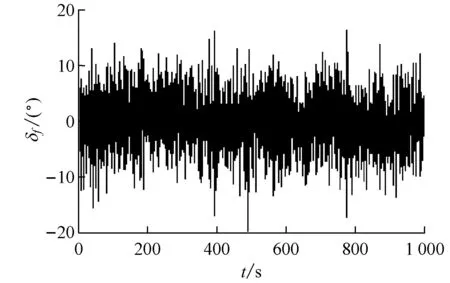
b) 非线性反馈控制的控制输出
(8)
根据文献[2],有
(9)
则
(10)
故正弦函数驱动的非线性反馈不对系统的稳态产生额外影响。
3.2对系统的动态性能的影响
从系统输入r到系统输出y的传递函数为
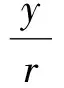
(11)
式(11)中:当ω=1时,相当于原鲁棒控制系统的输出响应;当ω≠1时,适当选择ω可改变系统的自然频率和阻尼比,从而改善系统的动态响应性能。
3.3对控制输出的影响
从系统输入r到控制器输出u的传递函数为
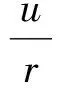
(12)
式(12)中:当ω<1时,相当于降低控制输出的自然频率并增加控制输出的阻尼(这里非线性反馈控制的控制输出频率由原来鲁棒控制的控制输出19.0 Hz降为16.7 Hz),降低控制输出幅值,从而达到节能的效果。
4 结束语
保持原有的基于闭环增益成形和镜像映射方法设计的鲁棒控制不变,通过引入正弦函数驱动的非线性反馈,对MIMO形式的水翼艇控制系统进行完善,取得控制效果和节能效果均比原鲁棒控制好的仿真结果,控制效果比鲁棒控制器提升70%以上,控制能量比鲁棒控制器节省90%以上。该研究只对误差较小时非线性反馈能改善系统输出性能并节能的简单理论进行分析,后续工作中将进行更深入的理论分析。
[1] 赵希人,叶葵,陈虹丽,等. 水翼艇纵向运动多变量随机最优控制仿真[J]. 船舶工程, 2003, 25(4):38-42.
[2] 张显库.水翼艇纵向运动多变量鲁棒控制[J].中国造船,2009, 50(4):203-207.
[3] 张显库.船舶运动简捷鲁棒控制[M].北京:科学出版社, 2012:1-15.
[4] ZHANG Xianku, ZHANG Guoqing. Stabilization of Pure Unstable Delay Systems by the Mirror Mapping Technique [J]. Journal of Process Control, 2013, 23(10):1465-1470.
[5] 李子昀,杨理华. 高速水翼船运动姿态控制研究[J]. 船舶工程,2013,35(3):10-15.
[6] 王宇超,刘胜,苏旭. 水翼双体船纵向运动鲁棒增益调度控制研究[C]//第三十三届中国控制会议论文集(B卷).北京:中国自动化学会控制理论专业委员会、中国系统工程学会,2014.
[7] 张松涛,孙明晓,梁利华,等. 穿浪双体船T型水翼状态反馈H∞控制器设计[J]. 舰船科学技术,2014,36(10):78-82.
[8] BAI Jangwhan, KIM Yonghwan. Control of the Vertical Motion of a Hydrofoil Vessel[J]. Ships and Offshore Structures, 2010, 5(3): 189-198.
[9] 张显库.用航向偏差的正弦函数驱动的自动舵控制算法[J].中国航海,2011,34(1):1-4.
[10] WOLFF J H. Model Investigation of the Stability and Control of PCH[R]. David Taylor Model Basin, Report C-1258, 1961.
RobustControlofLongitudinalMotionforHydrofoilsBasedonNonlinearFeedback
ZHANGXianku
(Navigation College, Dalian Maritime University, Dalian 116026, China)
2015-12-28
国家自然科学基金(51109020);中央高校基本科研业务费专项资金(3132014302)
张显库 (1968—), 男, 辽宁辽阳人,教授,博士生导师,从事舰船运动控制研究。E-mail: zhangxk@dlmu.edu.cn
1000-4653(2016)01-0060-04
U664.82
A
