钢管混凝土板柱节点弯矩分析

李志民

(中国建筑第二工程局有限公司,北京 100054)



钢管混凝土板柱节点弯矩分析

李志民

(中国建筑第二工程局有限公司,北京 100054)

利用有限元分析软件对钢管混凝土板柱铰接节点的应变、内力及变形进行了分析，结果表明：发生侧移时该节点附加弯矩很小，可认为此节点为铰接点，在对节点进行抗冲切设计时可不考虑节点附加弯矩的影响，只需进行重力荷载作用下的冲切设计。

板柱节点；钢管混凝土；弯矩

1　引言

板柱结构体系是一种在楼盖中不加设肋梁，楼板直接支撑在柱子上的一种结构形式[1]。钢管混凝土，钢管套箍混凝土是在钢管中填充混凝土后形成的构件，由于钢管混凝土结构形式简单，传力途径简捷、节约净高、工程施工进度快、可大幅度缩短工期等优点，多被用于高层混凝土结构中[2]。其节点不仅要承受结构自身的竖向荷载，还要承受诸如风荷载、地震荷载等类似水平荷载(位移)的作用，这就需要节点不仅要满足规范的要求，还需与结构一起承受变形。传统的钢筋混凝或者钢管混凝土板柱节点为刚节点形式，即混凝土板与节点浇注在一起。此类节点的构造形式使得节点构造复杂节点受力不明确，难以形成一种完善的理论体系。笔者的试验借助有限元分析软件ADINA对新型钢管混凝土板柱铰接节点的应变、内力及变形进行了分析。可为钢管混凝土板柱结构体系在高层建筑中广泛应用提供一定依据。

2　板柱节点设计及内力分布

试验所采用的柱板节点在发生侧向移动时，托板在重力和局部弯矩的作用下发生塑性变形，使节点的局部弯矩保持在相对较小的水平上，而其局部弯矩由托板上的竖向应力差来平衡。柱板节点的托板焊接在钢管外壁上，托板的厚度为20 mm，伸出外壁60 mm。试件浇注后混凝土外皮和托板底部平行。试验所采用的节点形式如图1所示。

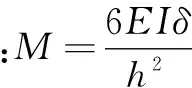
图1　节点构造形式

图2　节点受力

试验中假定混凝土楼板在受到水平荷载的作用下仅发生水平移动，故变形仅发生在托板内。节点的侧移能力完全取决于托板的变形能力，节点局部弯矩的大小取决于托板承载力和混凝土板的抗剪承载力。节点的变形能力取决于托板的塑性变形，托板的塑性变形越大，钢管混凝土柱端的转动越大层间侧移越大。一般节点不平衡弯矩是由板内弯矩和在临界截面的扭矩共同承担，而此节点则是由板作用在托板上的竖向力来平衡，所以此节点的受力明确，但其抗变形能力取决于托板的塑性变形能力。

3　托板承载力和变形分析

3.1弹性阶段

弹性阶段进行设计时，节点部位受力呈现线性分布，且节点应变恰好出现屈服，作用在节点上的最小的应力值为0。 其 节点最大最小应力计算公式为：

(1)

式(1)中,Nb—作用在试件节点下部压力值，kN；Nt—作用在试件节点上部的压力值，kN；Mb—作用在试件节点下部的附加弯矩值，kN·m；Mt—作用在试件节点下部的附加弯矩值，kN·m；AA—为托板的面积，mm2。

因为试件下部为铰接形式，且节点上部没有施加竖向荷载，故节点最大最小应力表达式改写为：

(2)

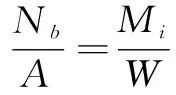
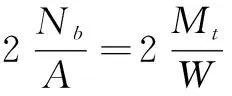
弹性状态下，节点应力及钢管右侧受力分别如图3、4所示。

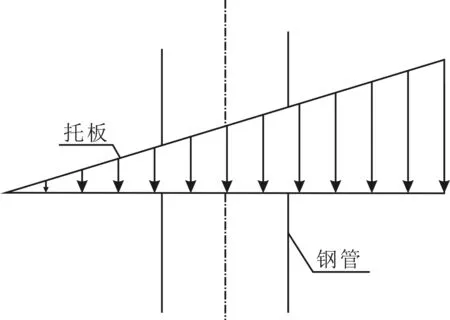
图3　应变图示

图4　托板右侧应力

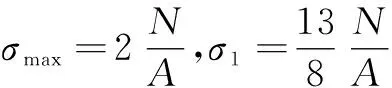
由叠加法则可得：

M总=M均布+M三角

(3)

根据罗氏应力应变公式可得：

(4)

(5)

由式(4),(5)可得，在此弹性阶段时，作用在节点部位竖向力最大值的计算公式为：

(6)

式(6)中，

(7)

(8)

(9)

节点受到不平衡弯矩值的大小可以按照如下方法计算：当GSR≤0.6时，计算只需对受力较大的一端进行分析，弹性阶段不平衡弯矩公式可用罗氏应力应变公式中弯矩计算公式进行计算，计算式如下：

M总=M均布+M三角

(10)

(11)

(12)

将上述计算过程应用到该试件中，可得作用在托板上的最大的应力值和不平衡弯矩的大小值。托板外径160mm，约为6.299in；内径100mm，约为3.937in。荷载加载位置r0=b=100mm=3.937in；托板泊松比为0.3。

按照上述公式，将数值代入上述公式当中可得：C8=0.7865，C9=0.258，L17=0.055，L18=19.6。

将上述数据代入弯矩总公式当中可得：

M总=3.6q1-2.45q2

(13)

式(13)中，q1=4.82N(1b/in2);

q2=1.1N(1b/in2)

将q1;q2数值带入到M总中：

M总=-3.6×4.82N-2.45×1.1N=20N(1b-in/in)

(14)

式(14)中，最大的应力值为：

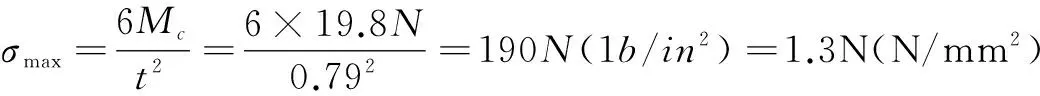
当最大的应力值σmax=210时，此时得到的竖向力N为：

当竖向力值为162kN时，因为，

A=3.14×(1602-1002)=48984mm2

由上述计算可知，当作用在节点上的竖向力为162kN，作用在节点上的弯矩值为8kNm时托板刚刚开始屈服，此时作用在托板上最大的压强值为6.6MPa。

3.2 塑性阶段

若对托板按照塑性进行设计，根据钢板材料的性质，其塑性指数为1.4～1.7，取塑性指数下限，则此时不平衡弯矩值取M塑性=1.7M总进行设计。若要按照托板塑性进行设计，当GSR>0.6时，由于节点受到的竖向力值接近于冲切强度数值，使节点在承受竖向荷载之外用来抵抗 侧向变形的能力降低，此时节点的破坏主要取决于混凝土的抗剪能力，因此，在当GSR>0.6时：

(15)

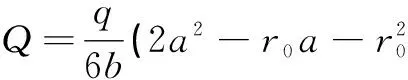
试验中节点最终破坏比较突然，且节点破坏后出现明显的冲切锥，节点处混凝土被冲出，说明当竖向力加载数值较大时若接近混凝土抗剪强度极限值时节点的抗侧移能力会明显降低，因此设计当中不建议GSR值超过0.6。

4　托板应力及变形有限元分析

通过ADINA软件对柱板节点托板受力情况进行分析，由分析结果可知，钢管在整个试验过程中受力较小，因此节点只需对托板进行分析。托板模型以及受力情况如图5、6所示。托板上受到线性均布荷载的作用，其最大值为6.7 MPa，最小值为0。模型内部为固定端，外缘为自由端。

计算后托板的应力情况如图7所示。此时，恰好托板上刚刚出现屈服点，与假定计算结果比较相符。图8为节点最大位移放大10倍后托盘位移变化图，托板最大的位移为0.085 mm，托板竖向变化不大。

由上述分析可知，当节点受到竖向力为162 kN，不平衡弯矩为8 kN·m时节点受力恰好达到托板受力的这样一个弹性受力状态，此时GSR=0.5。

图5　荷载形式

图7托板应力

图8　托板位移变化

5　结论

(1)试验中节点最终破坏比较突然，且节点破坏后出现明显的冲切锥，节点处混凝土被冲出，说明当竖向力加载数值较大时若接近混凝土抗剪强度极限值时节点的抗侧移能力会明显降低，因此设计当中不建议GSR值超过0.6。

(2)节点受到竖向力为162 kN、不平衡弯矩为8 kN·m时，托盘开始屈服，节点受力达到托板的弹性受力状态，此时GSR=0.5，故建议设计中GSR为0.5。

(3)节点发生侧移时节点的附加弯矩很小，可以认为此节点为铰接点，设计中可按照铰接进行设计，即此类节点在水平作用下不会产生附加弯矩，在对节点进行抗冲切设计时不考虑节点的附加弯矩的影响，只需要进行重力荷载作用下的冲切设计。

[1]蔡绍怀. 现代钢管混凝土结构[M]. 北京：人民交通出版社，2003：1.

[2]蔡绍怀. 钢管混凝土结构[M]. 北京：中国建筑科学研究院，1992：4～5.

Analysis on the Bending Moment of Steel Pipe Column-Slab Connection

Li Zhimin

(ChinaConstructionSecondEngineeringBureauLtd.,Beijing100054,China)

The strain, inner force and deformation of the joint in slab-column connection was studied with the help of ANINA. The result showed that the additional bending moment was low and could be regarded as a hinge. When designing the punching resistance, we could only conduct the design under the gravity load regardless of the additional bending moment of the connection.

slab-column connection; steel-pipe concrete; bending moment

2016-08-10

李志民(1978—)，男，助理工程师，主要从事建筑结构力学方向的相关工作。

TU37

A

1674-9944(2016)16-0224-04