降雨型滑坡的集合预报模型及其初步应用的试验研究

陈悦丽 陈德辉 李泽椿 吴亚丽 黄俊宝



降雨型滑坡的集合预报模型及其初步应用的试验研究

陈悦丽1, 2, 3陈德辉3李泽椿4吴亚丽5黄俊宝6

1南京信息工程大学大气科学学院，南京210044m,2中国气象科学研究院灾害天气国家重点实验室，北京100081,3中国气象局数值预报中心，北京100081,4国家气象中心，北京100081,5中国气象局广州热带海洋气象研究所区域数值预报重点实验室，广州510080,6福建省地质环境监测中心，福州350002

滑坡的实时预警系统GRAPES-Landslide是将数值天气预报模式GRAPES（Global/Regional Assimilation and PrEdiction System）与滑坡预测模型TRIGRS（Transient Rainfall Infiltration and Grid-based Regional Slope- stability）进行单向耦合建立起来的动力数值预报预警系统。由于滑坡预测模型TRIGRS中的关键水土参数具有空间分布很不均的特性，很难获取准确的数据加以描述，使得滑坡事件的激发、预测存在很大的不确定性，同时数值天气预报模式本身具有不确定性，因而用于诱发滑坡灾害的估测降水存在不确定性，进而使得滑坡的预报存在偏差。本研究基于预测降水和水土参数分布不确定性的考虑，提出了GRAPES-Landslide滑坡集合预报模型。滑坡集合预报模型中有5个不同的预报降水成员，分别是（1）GRAPES_MESO业务模式、（2）“暖—潜热加热纳近”方法、（3）基于九点平滑滤波的“暖—潜热加热纳近”方法、（4）对（1）～（3）的降水成员进行简单平均、（5）对（1）～（3）的降水成员进行概率匹配的集合。根据水土参数呈正态分布的特点，通过Monte-Carlo方法随机生成100组扰动参数值。将5个预报降水与100组扰动水土参数结合，组成GRAPES-Landslide滑坡集合预报模型。选择2013年7月18日00时到7月19日12时（协调世界时）福建省“西马仑”台风降雨引发闽三角地区发生大量滑坡灾害为例，进行实际预报试验。初步研究结果表明本文建立的GRAPES-Landslide滑坡集合预报系统所预测的滑坡频发区与观测区域有很好的吻合度，与目前的滑坡业务预报结果相比有明显改进，落区更精细化。因此，GRAPES-Landslide滑坡集合预报系统综合考虑了降水预报的不确定性和非均匀分布的水土参数的不确定性，为区域滑坡预测提供了一种新的可能方法。

降雨型滑坡 GRAPES-Landslide预报系统 集合预报

1 引言

滑坡灾害是全球泛生型突发性地质灾害，广泛分布于高山、中山和低山丘陵区。影响滑坡的主要因素可以分为内因和外因两类：内因包括地质条件、地貌类型和人类活动；外因包括降水、地震和火山爆发等（Varnes，1978）。根据我国县市地质灾害第一期调查的结果显示，滑坡的主要诱发因素是暴雨，暴雨诱发的滑坡数量占总数的90%（李媛等，2004）。早期的研究也显示滑坡的发生与降水的时空分布具有紧密的联系。目前开展的滑坡预测研究主要基于经验模型、统计模型或者动力模型。

经验模型主要分析诱发滑坡发生的降雨特征，特别是降雨强度、历时和累积雨量，获得诱发滑坡的降雨强度——历时关系曲线（Intensity-Duration curve，简称I-D曲线）或者累积雨量的临界值，从而判断滑坡发生的可能性。经验模型的特点是简便，易于操作，但是只能适用于特定的区域。统计模型包括贝叶斯模型、回归模型和神经网络模型等。统计模型减少了选择降雨阈值的主观性，考虑了静态条件，例如坡度、海拔高度和植被覆盖等因素，但是不适合用于研究极端降水诱发的滑坡事件，并且无法对滑坡发生的内部机理进行解释。动力模型从模拟滑坡发生的物理机制出发，一般以地理、地质和水文特征作为输入参数，降水作为驱 动因子。将水文模型与边坡稳定性模型进行耦 合，可以较好的模拟坡体的变化。目前常用的耦合模型有SHALSTAB（SHAllow Landslide STABility model）、SINMAP（Stability INdex MAPping）、dSLAM/IDSSM（distributed Shallow LAndslide Model/Integrated Dynamic Slope Stability Model）和TRIGRS（Transient Rainfall Infiltration and Grid- based Regional Slope-stability model）等。与其他模型相比较，TRIGRS模型考虑了瞬态降水过程对边坡稳定性的影响，模拟结果更为准确（Godt et al., 2008）。

TRIGRS模型基于瞬态降雨入渗原理，模拟边坡安全系数随时间的变化（Iverson，2000；Baum et al., 2008）。Chen et al.（2005）使用TRIGRS模型模拟了2000年12月发生在台湾的一起由降雨诱发的滑坡事件。丛威青等（2008）将TRIGRS模型应用于我国南方某典型地区，结果表明该模型可以动态的预测区域降雨型滑坡的发生发展过程。Liao et al.（2011）在卡罗莱纳州北部梅肯县蓝岭山量化评估了Matlab版本TRIGRS的时空预测能力，结果显示在准确的降雨预报和详细的野外数据基础上，此模型具有较高的滑坡预警潜力。Kim et al.（2010）利用分辨率为5 m×5 m的DEM（Digital Elevation Model）数字高程模型和土壤调查数据，使用TRIGRS模型计算安全系数，得到可能发生滑坡的区域，并且与分辨率为1 m×1 m的IKONOS2滑坡遥感图像进行对比分析，两者的符合度为64.1%。Vieira et al.（2010）使用TRIGRS模型预测位于巴西圣保罗的马尔山流域的不同场景下的浅层滑坡。Godt et al.（2008）应用TRIGRS模型在华盛顿州的西雅图北部进行模拟，结果表明加入瞬态过程提高了模型的模拟精度。滑坡动力模型的预报效果已经得到了国内外学者的认可，但是将滑坡动力模型应用到实际的预报工作中仍然有很多问题需要解决，特别是如何获取高时空分辨率的预测降雨数据和水土参数。

目前滑坡预报研究中使用的降雨数据主要来自气象观测站。使用气象观测站的降雨资料进行滑坡预报，存在以下三个问题：（1）观测降水资料不是预测资料；（2）气象站点数量有限且分布不均；（3）部分高山或者偏远地区，缺乏降雨观测资料。部分学者提出利用数值天气预报模式预报降水，从而驱动滑坡模型，预测滑坡发生的时间和地点。Liao et al.（2010）用空间分辨率为4 km×4 km的WRF（Weather Research Forecasting）模式的预报降水数据驱动滑坡预测模型SLIDE（Slope-Infiltration- Distributed Equilibrium），成功的预测了滑坡发生的时间。魏丽（2005）利用MM5中尺度数值预报系统（Fifth-generation Pennsylvania State University– National Center for Atmospheric Research Mesoscale Model）对诱发滑坡的连续降水进行数值试验，获取定量定点降水预报产品，使用统计模型进行滑坡预报。数值天气预报模式可以预测未来降雨的时空分布特征，但是存在一定的误差。数值天气模式的误差主要来自初始条件和模式本身。数值模式的初始条件只是真实大气状态的一个近似，初始场的一个细微差别可能导致结果产生很大差异。从单一确定的初始场得到的预报结果仅仅是真实大气的一个可能解，存在着不确定性和不可靠性等问题（肖玉华等，2011）。集合预报为解决单一预报不确定性问题提供了一种可能的方法。

由于滑坡预测模型中的关键水土参数具有空间分布不均的特性，很难获取准确的数据加以描述，使得滑坡事件的激发、预测存在很大的不确定性。前人的研究显示凝聚力和内摩擦角是模型不确定性的主要来源（Chowdhury and Flentje, 2003; Griffiths et al., 2011），并且通常呈正态分布（Vanmarcke, 1977; Wang et al., 2010; Park et al., 2012），因此可以将获取高空间分辨率的水土参数的需求，转化为获取水土参数的概率密度分布曲线。传统的滑坡预报方法通常只能预报出百公里的地质灾害易发区，而将集合数值天气预报方法与动力学地质灾害模型相结合，进行滑坡的概率预报，可以提高滑坡的空间预报到公里级别与延长滑坡预报预见期。滑坡的实时预警系统GRAPES- Landslide是将数值天气预报模式GRAPES（Global/ Regional Assimilation and PrEdiction System）与滑坡预测模型TRIGRS进行单向耦合建立起来的动力数值预报预警系统（Chen et al., 2016）。本文基于预测降水和水土参数分布不确定性的考虑，提出了GRAPES-Landslide滑坡集合预报模型。选择2013年7月18日00时至7月19日12时（协调世界时，下同）“西马仑”台风降雨过程诱发福建省闽三角地区发生的大量滑坡为例，进行滑坡预报试验。

2 研究区域和“西马仑”台风简介

福建省位于我国东南沿海，是典型的亚热带季风气候，雨季降雨量占全年降雨量的30.0%左右，多年7月的平均降雨量为190 mm。闽三角地区位于福建省的东南部，包括泉州市、厦门市和漳州市，地形西高东低，特别是沿海地区海拔较低，多为 400 m以下，坡度在0°～74°之间，集中分布在30°以下（图1、图2）。地质类型主要有6种，包括沉积岩与变质岩的元古界、古生界、中生界地层，以及岩浆岩中的花岗岩、镁铁质岩类和火山岩（图3，数据来源于地球系统科学数据共享平台——中国1:400万全要素基础数据）。其中以沉积岩与变质岩的中生界地层和花岗岩为主，占总面积的90%以上。

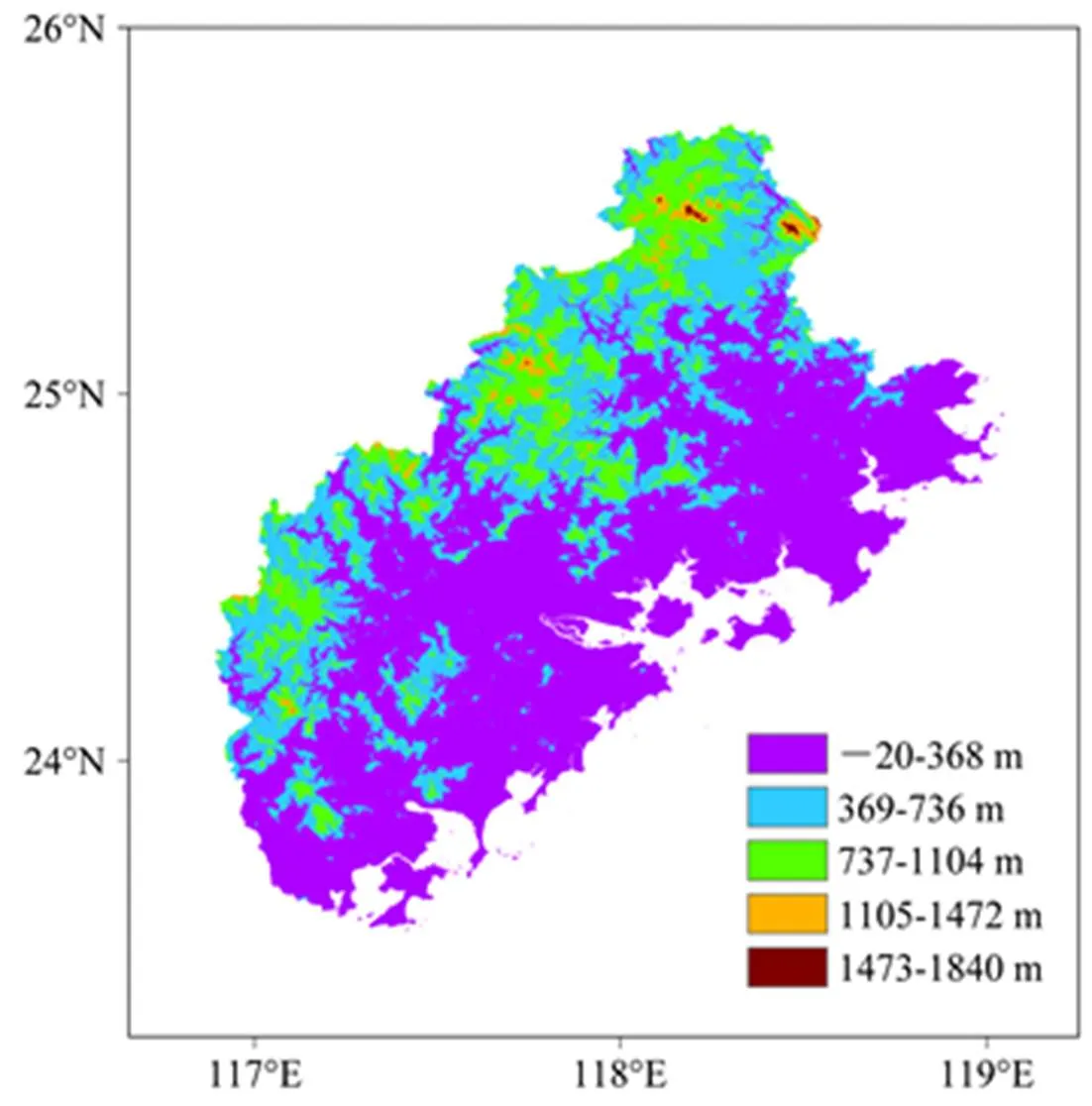
图1 闽三角区域的海拔高度分布（单位：m）

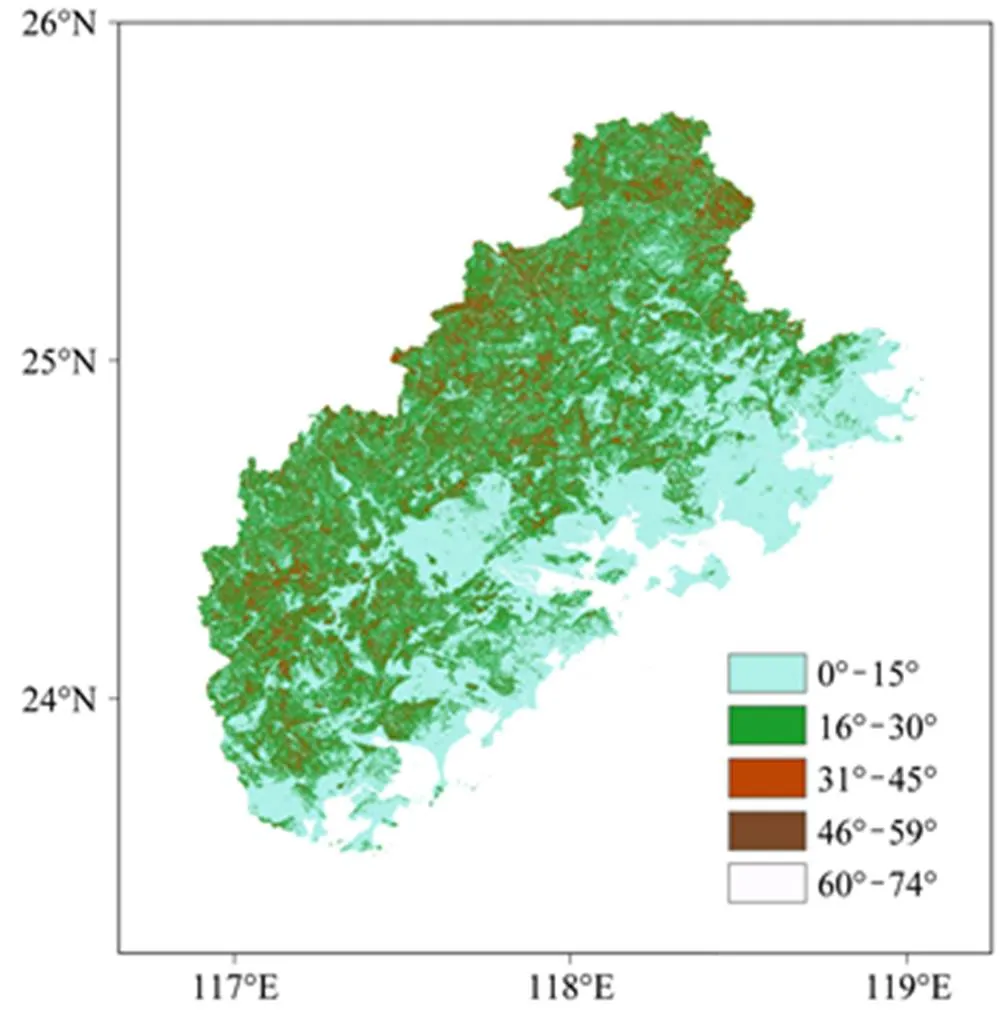
图2 闽三角区域坡度分布

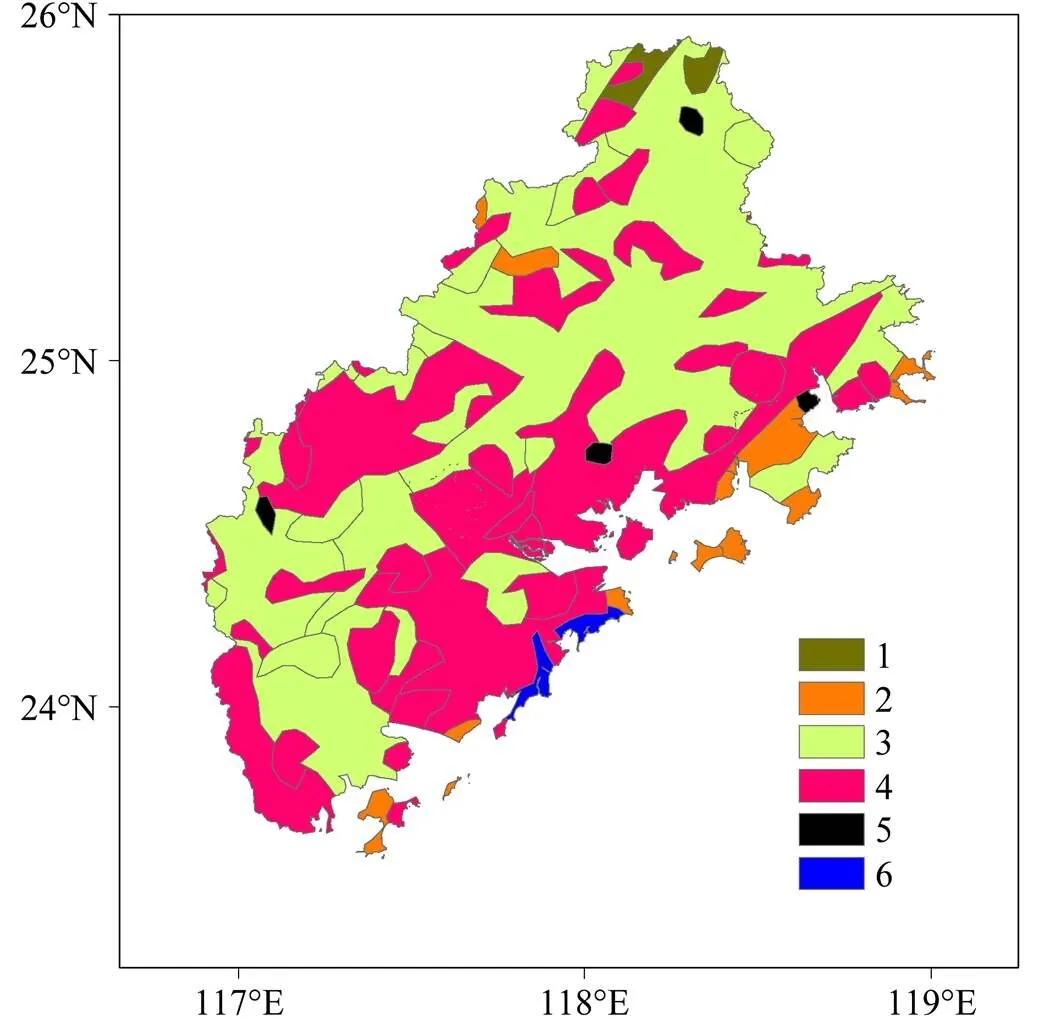
图3 闽三角区域地质类型。色标1、2、3、4、5和6分别表示元古界（沉积岩与变质岩）、古生界（沉积岩与变质岩）、中生界（沉积岩与变质岩）、花岗岩（岩浆岩）、镁铁质岩类（岩浆岩）和上新世—全新世火山岩（岩浆岩）

2013年第8号热带风暴“西马仑”于7月18日12时30分在福建省漳浦县登陆，18日18时在福建省华安县减弱为热带低压，18日21时停止对其编号（图4）。由于受台风“苏力”的影响，“西马仑”台风登陆前，福建省的10日累积降雨量高达到222 mm（图5，数据来源于中国气象科学数据共享网——中国地面降水日值0.5°×0.5°数据集V2.0），土壤已经呈饱和或者近饱和状态。“西马仑”台风降雨过程在闽三角地区诱发了大量的滑坡灾害，有20.28万人受灾，直接经济损失15.52亿元。

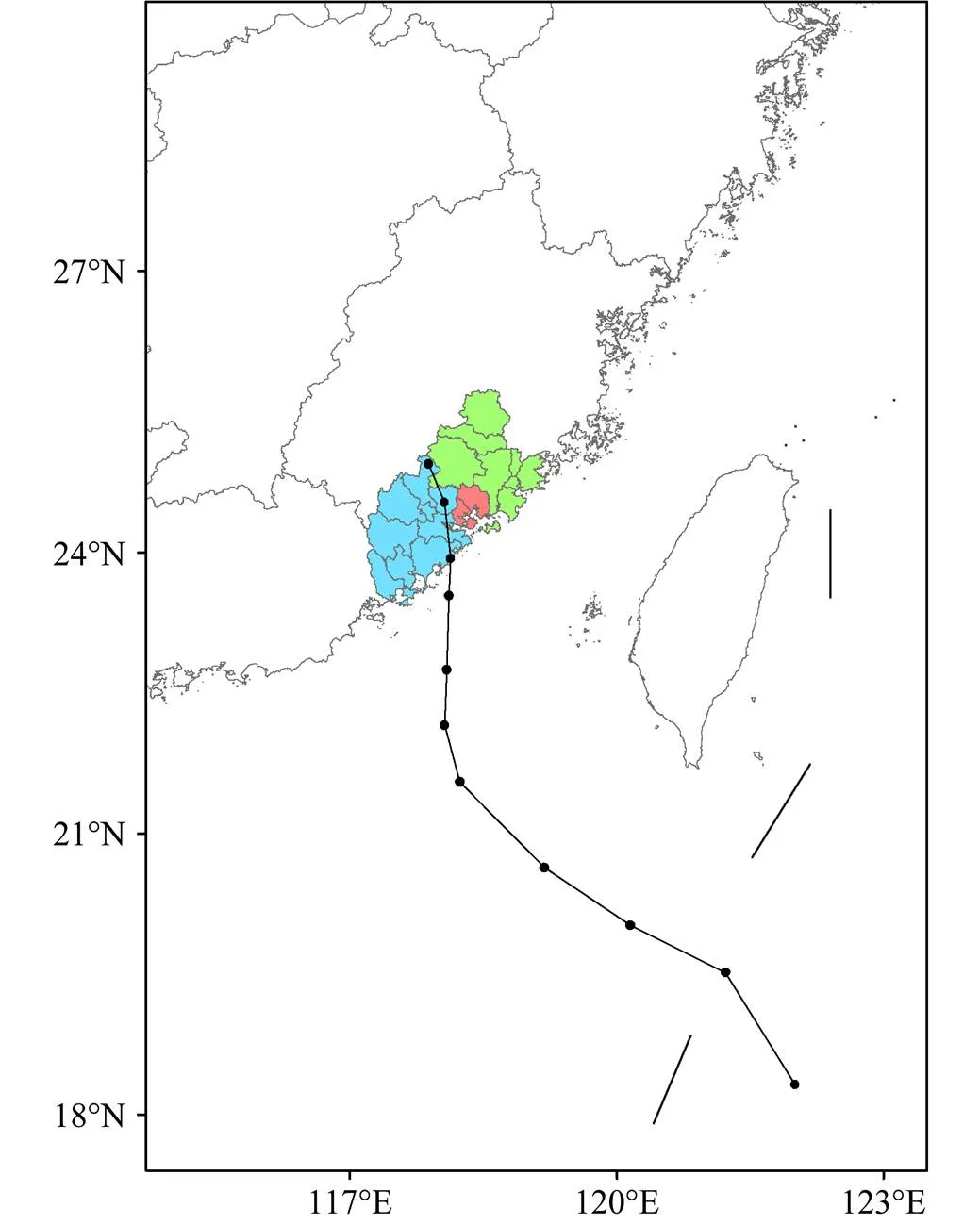
图4 “西马仑”台风路径以及闽三角地区（绿色：泉州市；红色：厦门市；蓝色：漳州市）的地理位置。

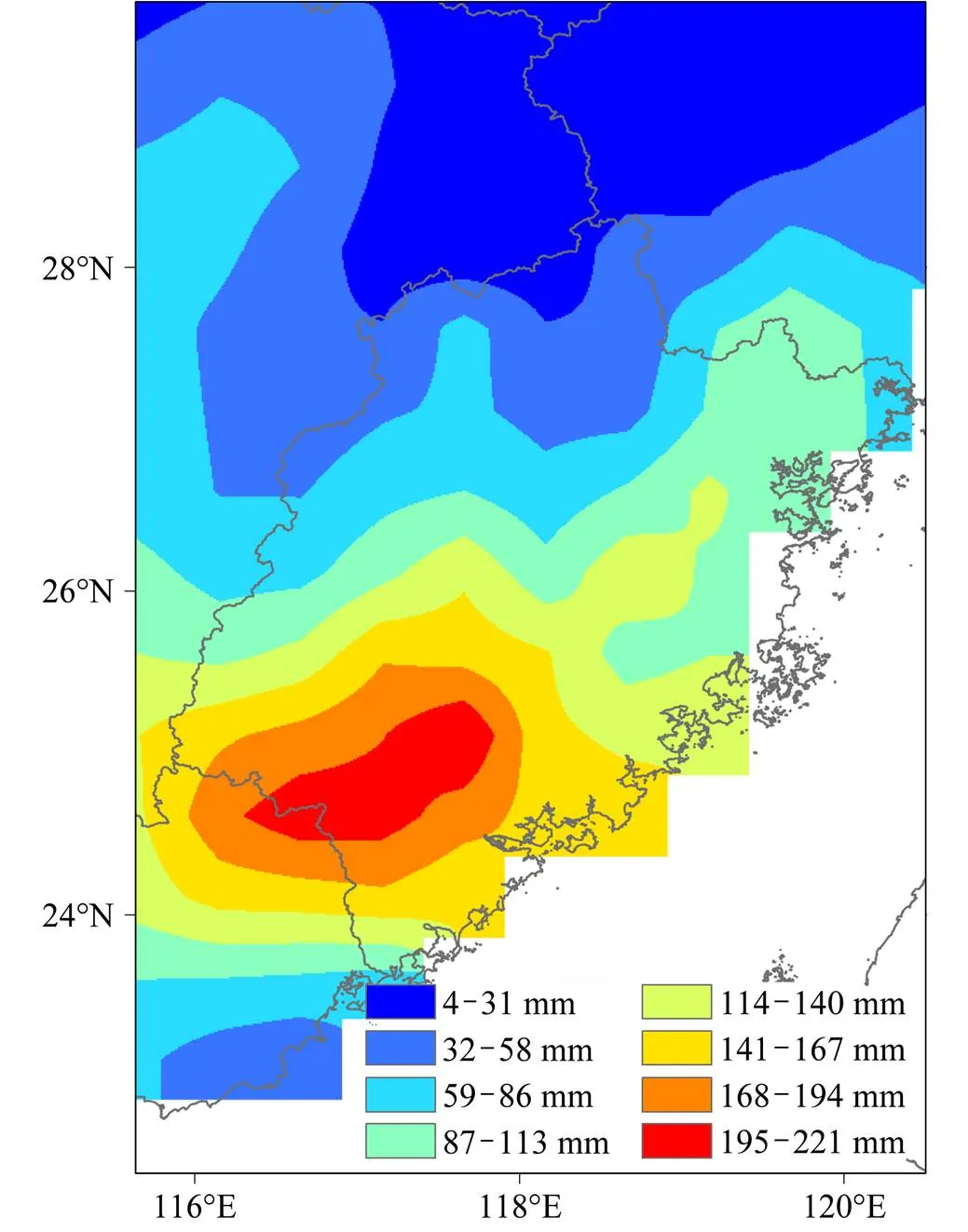
图5 2013年7月8日至2013年7月17日福建省及其周边区域累积降雨量（单位：mm）

3 基于GRAPES-Landslide的区域集合预报模型

GRAPES模型是2001年中国气象局联合各个高校、研究所的专家建立的数值天气预报系统，如今已经实现了业务运行，表现出较好的预报技巧（Zhang and Shen, 2008）。TRIGRS模型是由美国地质调查局开发的降雨诱发型滑坡的预报模型。滑坡的实时预警系统GRAPES-Landslide是将GRAPES模型的逐小时降水预报结果经过降尺度后驱动TRIGRS模型。目前该预警系统已经在福建省德化县进行了初步的试验，结果显示该预警系统对降水诱发型滑坡具有较好的预报能力（Chen et al., 2016）。

GRAPES-Landslide模型的滑坡预报准确度主要取决于降水预报的准确性、水土参数精度以及模式本身。利用数值天气预报模型进行降水预报具有不确定性，预报的不确定性主要来自模式本身以及初始条件。初始条件只是真实大气的一个近似，对初始场进行扰动，开展集合预报可以在一定程度上解决降水预报的不确定性问题。同时，由于缺乏高精度的水土参数的空间分布信息，极大地限制了模型的使用范围。如果根据野外调查的数据，对水土参数进行适当的扰动，就可以将模型应用于较大的区域。基于滑坡的实时预警系统GRAPES- Landslide，考虑模型降水预报和水土参数的不确定性因素，提出了GRAPES-Landslide滑坡集合预报模型，将传统的滑坡预报由确定性预报发展为概率预报。

3.1 GRAPES模式的初值不确定性扰动

滑坡预报模型需要降水数据作为驱动因子。本研究基于GRAPES_MESO模式，使用5个不同的降雨预报成员，进行降雨预报：

（1）GRAPES_MESO业务预报模式。

（2）采用潜热加热纳近方法融合加密自动站的降水资料，调整模式的加热廓线，使模式降水向观测降水逼近，进而调整模式预报的初始场，达到改进模式初值的目的，从而提高降水预报准确度。进行地面降水资料同化之前，GRAPES模式先运行 3 h，这样就有较为合理的模式雨带与观测雨带进行匹配，然后再修正模式的加热廓线，这种方法被称为“暖—潜热加热纳近”方法（吴亚丽等，2015）。

（3）在“暖—潜热加热纳近”方法的基础上，利用九点平滑滤波的方法对初始场进行平滑，这种方法被称为“基于九点平滑滤波的‘暖—潜热加热纳近’方法”。

（4）将（1）～（3）的降水预报结果进行简单的集合平均。

（5）将（1）～（3）的降水预报结果通过概率匹配的方法进行集合。

第1个降水预报成员是基于GRAPES业务预报模式。第2个降水预报成员的特点是同化了加密自动站的降水资料，调整了模式的加热廓线。第3个成员是在第2个成员的基础上，对初始场进行九点平滑滤波。第4和5个成员分别用简单平均和概率匹配的方法对前三种不同初始场的降水预报结果进行集合。

3.2 TRIGRS模型及其参数扰动

TRIGRS是基于栅格的降雨诱发型斜坡稳定性计算模型，包括入渗模型、斜坡稳定性模型和水文模型三部分。Iverson（2000）提出了瞬时降雨入渗模型，并将瞬时降雨入渗模型与无限边坡稳定性分析模型及牛顿第二定律结合起来，预测滑坡发生的时间和地点。Baum et al.（2008）发展了Iverson（2000）模型，增加了复杂降雨过程的解决方案。

3.2.1 入渗模型

入渗模型应用于饱和或者近饱和的试验区域，包括稳定入渗部分和瞬态入渗部分。稳定入渗部分取决于地下水位的初始深度和稳定入渗速率，可见入渗模型对初始条件十分敏感，因此需要进行田间试验获取较为准确的初始条件。瞬态入渗部分假设水流一维竖直向下流动，并且随着降雨强度的变化而变化。有限深度不渗透底部边界的压力水头的公式（Baum et al., 2008）为

3.2.2 斜坡稳定性模型

利用无限边坡模型分析斜坡的稳定性。无限边坡是对土层深度远远小于斜坡的长或宽的复杂斜坡形态的简单近似。无限边坡的初始破坏通过平衡方程描述，重力沿斜坡向下的分力与依照库伦准则获得的抵抗力之间相互平衡（孔隙水压力作为中间媒介）。安全系数S（Factor of Safe）定义为（Iverson, 2000）

3.2.3 水文模型

TRIGRS模型使用了基于简单水量平衡的水文模块来模拟地表径流，这样可以防止降雨所产生的地表径流在运算域的网格中消失。模型中假设每一个运算时间域内质量守恒，凡是无法在目前时间域内入渗的降雨，将以地表径流的方式流往运算域内下游网格，具体的计算方法参见式（4）和式（5）（Baum et al., 2008）。

当地表径流流至新网格时，根据该网格当时的含水量，可以选择下渗或是继续向下游网格前进。模式中假设如果降雨量加上来自邻近网格的地表径流量之和超过该网格的入渗容量时，该网格随即产生地表径流，流向下游临近网格。

3.2.4 TRIGRS模型的参数扰动

TRIGRS模型被广泛地应用于降雨型滑坡预测。通常预报区域面积较小，一般为几平方千米。在较小的预报区域内，可以通过开展大量的野外采样工作和室内试验获得水土参数值。但是滑坡预测模型TRIGRS中的关键水土参数本身具有内在的空间分布非均匀性（Baecher and Christian, 2003; Chowdhury et al., 2010），即使是在同层土中不同位置的水土参数也具有变异性。如果模型采用单一的参数值，容易导致预报结果存在偏差。当预报区域范围较大时，获取准确的高精度水土参数几乎是不可能的，使得滑坡事件的激发、预测存在很大的不确定性。因此必须解决在水土参数空间分布不均以及采样样品有限的条件下，如何利用有限的样本获取模型的输入参数的问题。

水土参数中内摩擦角和凝聚力是边坡稳定性模型不确定性的主要来源，本研究中只考虑了内摩擦角和凝聚力的空间分布不确定性。大多数学者的研究显示凝聚力和内摩擦角呈正态分布，也有部分学者认为凝聚力和内摩擦角呈线性或者对数正态分布（Vanmarcke, 1977; Wang et al., 2010; Park et al., 2012）。将内摩擦角和凝聚力看作一个随机变量，根据其具有的某种分布特征，就可以将获取高精度水土参数空间分布的需求，转化为获取水土参数的概率密度分布曲线，从而解决获取水土参数困难的问题（Park et al., 2013; Raia et al., 2014）。

蒙特卡洛方法（Monte-Carlo）是以概率统计理论为基础，实现从已知概率分布抽样，建立随机变量的估计值，构造符合一定规则的随机数。首先在野外采集土壤样品，然后通过实验室分析得到样品的凝聚力和内摩擦角。根据凝聚力和内摩擦角的分布特征，利用Monte-Carlo方法进行随机抽样。将每一组凝聚力和内摩擦角参数值都输入模型中计算安全系数，然后统计每个研究单元中安全系数小于1的次数，最后计算研究单元的失稳概率：

式中，s为滑坡发生的概率或者称为失稳概率，为随机抽样的次数，为随机试验中安全系数S小于1的次数。

TRIGRS模型通过将入渗模型、水文模型和斜坡稳定性模型耦合在一起，计算边坡的安全系数S，根据安全系数是否小于1来判断滑坡是否发生以及发生的时间，但是没有考虑岩土中客观存在的参数不确定性问题。利用参数的分布特征，通过Monte-Carlo方法模拟参数的随机分布，建立在概率论基础上的可靠度被引入到边坡的稳定性评价中，使得滑坡的预报方法由确定性预报，改进为概率预报，预报结果更为科学和精确。

4 模型应用

4.1 试验设计

GRAPES-Landslide滑坡集合预报模型中有5个不同的预报降水成员，主要包括：（1）GRAPES_ MESO业务预报模式；（2）“暖—潜热加热纳近”方法；（3）基于九点平滑滤波的“暖—潜热加热纳近”方法；（4）简单集合平均；（5）概率匹配的降水集合。在进行降水预报时，GRAPES模式垂直方向选取非均匀的32层，水平分辨率约为3 km。模式微物理过程选用WSM6类方案（水汽、雨、雪、云水、云冰、霰），长波辐射过程选用RRTM方案，短波辐射选用Dudhia方案，近地面层选用Monin- Obukhov方案，陆面过程选用Noah方案，边界层参数化方案为MRF方案，关闭积云参数化方案。“暖—潜热加热纳近”方法中使用的加密自动站降水资料来自于国家气象信息中心，该资料在由地方上传到国家气象信息中心之前，经过了各级资料部门的质量检查。模式的背景场和侧边界均由NCEP GFS的预报场提供，其中背景场为GFS的6 h预报场，侧边界条件每6 h更新一次，进行12 h的短时预报。

TRIGRS模型是基于栅格的模型，每个栅格的大小与DEM的空间分辨率一致。本研究中选用了空间分辨率为30 m×30 m的DEM资料（图1），也就是每个研究单元的空间分辨率为30 m×30 m。利用Monte-Carlo方法，根据闽三角地区的内摩擦角和凝聚力分布特征，随机生成100组数值，也就是每个研究单元都对应100组不同的水土参数组合。每一个降水成员做出降雨预报后采用双线性插值的方法进行降尺度后驱动TRIGRS模型。将5个预报降水与100组扰动水土参数结合，共进行5×100组试验，生成5×100个安全系数图层。每个研究单元都进行了5×100次试验，统计每个研究单元安全系数S小于1的次数，最后计算这个研究单元发生滑坡的概率。

4.2 输入参数

原始DEM矩阵中普遍存在洼地。为了使水流经过洼地时，有一个明确的水流方向，需要利用ArcGIS软件对DEM的洼地进行填平，然后采用单流向D8算法计算水流方向（Fairfield and Leymarie, 1991）。闽三角地区的坡度也是利用DEM资料在ArcGIS中直接提取（图2）。逐小时降水预报产品的空间分辨率约为3 km，使用双线性插值的方法降尺度到30 m。在台风“西马仑”登陆前十天，闽三角地区累积降雨量较大，最高可达到221 mm，其余区域也在100 mm以上。我们假设此时土壤已经处于饱和或者近似饱和的状态，水力扩散度0是水力传导度s的100倍，而入渗速率Z是s的0.01倍的（陈则佑等，2011；Liu and Wu, 2008；Chen et al., 2005）。

根据闽三角地区的地质分类图，该地区的主要地质类型为沉积岩与变质岩和岩浆岩（图3）。沉积岩与变质岩可以分为元古界、古生界和中生界等不同地层。岩浆岩可以分为花岗岩、镁铁质岩类和上新世—全新世火山岩等。对不同地质类型的分布面积进行统计，结果显示花岗岩占岩浆岩区域总面积的90%以上，沉积岩与变质岩的中生界地层也占沉积岩与变质岩区域总面积的90%以上。

德化县位于闽三角地区的最北部，其主要的地质类型为沉积岩与变质岩的中生界地层。2006年到2009年福建省地质环境监测院在德化县开展了水土参数调查工作，进行了大量的野外调查和室内试验。试验结果显示，土壤容重的平均值为12.73 kN m−3，土壤饱和水力传导度s为8.19×10−7 ms−1。根据此次调查工作获取的样本的凝聚力和内摩擦角数值，首先进行了正态分布拟合度测试，均通过了显著性水平为0.05的正态分布检验。将土样的实验结果利用Matlab软件进行正态分布拟合：凝聚力的平均值为12.21 kPa，方差为6.15；内摩擦角的平均值为21.06°，方差为6.18（图6）。这样的结果与其他学者的研究结论相符合，土壤参数具有正态分布的特征。从理论上说，Monte-Carlo方法需要大量的试验，试验次数越多，所得到的结果才越精确。考虑到模型运行的时间成本，本次试验中利用Monte-Carlo方法随机生成100组凝聚力和内摩擦角，作为闽三角地区沉积岩与变质岩区域的输入参数。

由于花岗岩占岩浆岩分布总面积的90%以上，因此岩浆岩区域的水土参数取值参考花岗岩区域的参数值。林蓬琪和侯萍（1990）等和王清等（1990）分析了闽三角地区花岗岩区域的水土参数分布特征。土壤容重的平均值为17.837 kN m−3，凝聚力的平均值为32.18 kPa，内摩擦角的平均值为27.8°，凝聚力和内摩擦角的方差都取6.2，具体的参数取值见表1。利用Monte-Carlo方法随机生成100组凝聚力和内摩擦角，作为闽三角地区岩浆岩区域的输入参数。

表1 模型输入参数

根据林蓬琪和侯萍（1990）的研究与实际勘测，当海拔高度小于400 m，假设土壤厚度为2 m；当海拔高度小于400 m，土壤厚度为2～10 m，假设土壤厚度与海拔高度呈线性关系= −0.02＋10，其中为海拔高度，为土壤厚度。闽三角地区的土壤厚度分布图见图7。根据经验判断，假设地下水位深度为土壤厚度的80%。

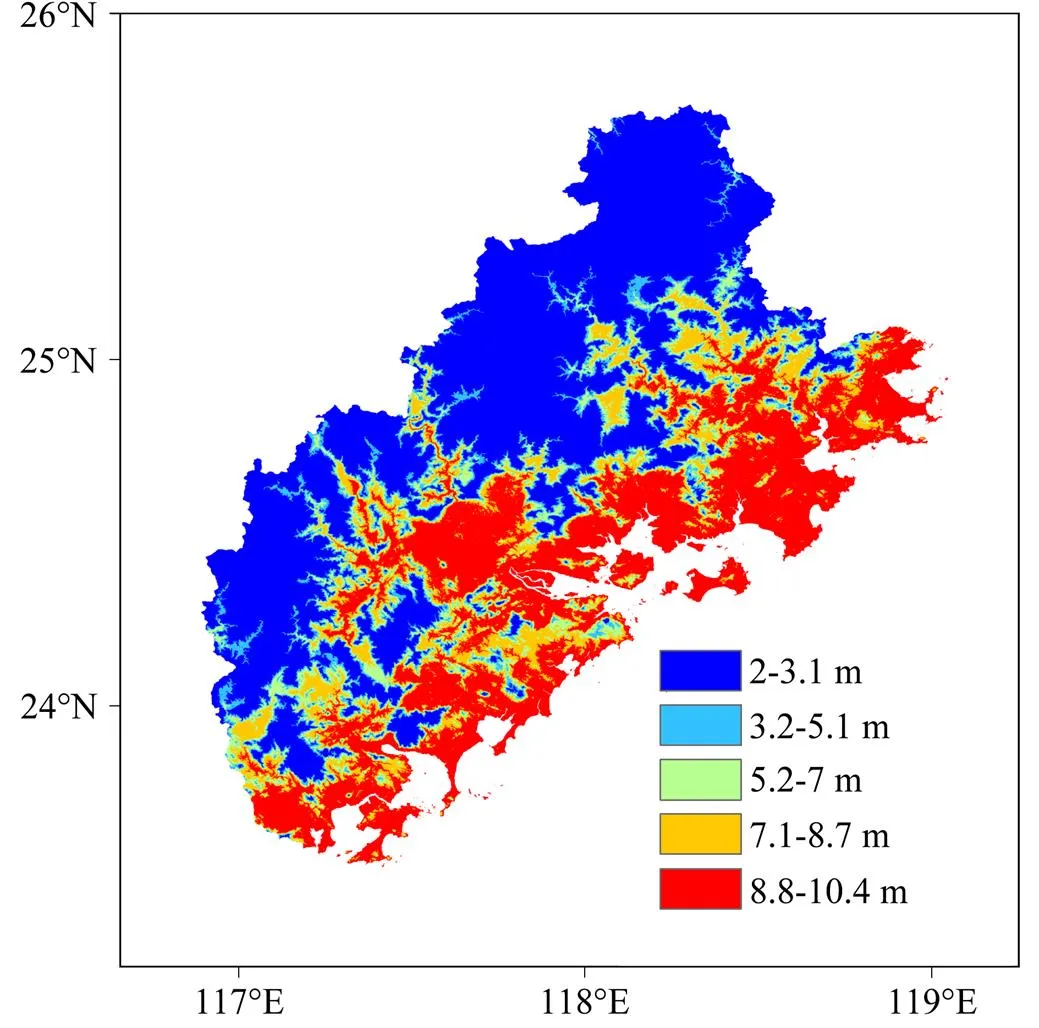
图7 闽三角地区土壤厚度分布（单位：m）

4.3 模拟结果

Chen et al.（2016）的研究结果表明：降水总量对预测滑坡可能发生的时间和地点具有显著影响；即使总雨量恒定，不同的雨型，例如逐小时降雨强度随时间递增或者递减，预测滑坡发生的时间差别很大。降水对滑坡具有明显的诱发作用，这就对降水预报的准确性提出了更高的要求，不仅需要准确预报降雨总量，还需要准确的预报逐小时降雨量。由于降水是多种尺度大气运动非线性相互作用的结果，大气的非线性和不稳定性特征所导致的预报误差增长意味着预报模式的初始条件的很小误差，都将不可避免的导致降水预报技巧的丧失，使得降水预报具有不确定性，因此使用多种方法获得不同的初始场可以减少降水预报的不确定性，提高降水预测的准确度。吴亚丽等（2015）的研究表明：“暖—潜热加热纳近”方法可以有效地同化地面降水资料，改进GRAPES模式12 h的降水TS（Threat Score）和ETS评分；采用概率匹配的方法对降水预报进行集合平均，可以提高GRAPES模式短时降水的预报准确性。在本研究中采用了不同的降水成员，包括GRAPES_MESO业务预报模式、“暖—潜热加热纳近”方法、基于九点平滑滤波的“暖—潜热加热纳近”方法、对前三个降水成员进行简单平均和概率匹配的集合。采用不同的成员进行降水预报，可以减小降水预报的不确定性。

模式的背景场和侧边界均由NCEP GFS的预报场提供，其中背景场为GFS的6 h预报场，侧边界条件每6 h更新一次，进行12 h的短时预报。图8中a1、b1、c1为观测的12 h累积降水量，由加密自动站点的小时降雨资料累加得到；a2、b2、c2为利用“暖—潜热加热纳近”方法进行降水预报的结果；a3、b3、c3为GRAPES_MESO业务模式的降水预报结果；a4、b4、c4为利用基于九点平滑滤波的“暖—潜热加热纳近”方法进行降水预报的累加12 h降水量；a5、b5、c5为对（a2、b2、c2）、（a3、b3、c3）和（a4、b4、c4）方法的逐小时预报结果进行了简单平均后进行累加；（a6）是采用概率匹配的方法对逐小时预报结果进行集合，然后对12 h的降水结果进行累加。“西马仑”台风于2013年7月18日12时30分在福建登陆。图8a显示了“西马仑”台风登陆前12 h降水总量，数值预报的降水落区和总量较实况都偏大。图8b显示了台风登陆后的降雨总量，与GRAPES业务预报模式相比，其余的四个降水成员都有效地改善了降水预报结果，预报雨带的位置与实况接近，特别是采用概率匹配的集合降水预报结果与实况更为接近。TS评分可以度量预报有降水和观测有降水事件被正确预报的比例。图9给出了2013年7月18日00时到7月19日12时的3 h、6 h和12 h累积降水的TS检验结果。GRAPES_MESO业务模型的降水预报TS评分显著低于其他四个降水成员，其他四个降水成员对小雨、中雨、大雨和暴雨的预报能力不同。不同成员预报的降水落区和强度存在一定差异。由于降水预报具有不确定性，利用多个成员的降水预报结果驱动滑坡预测模型，可以增大滑坡预报的准确性。

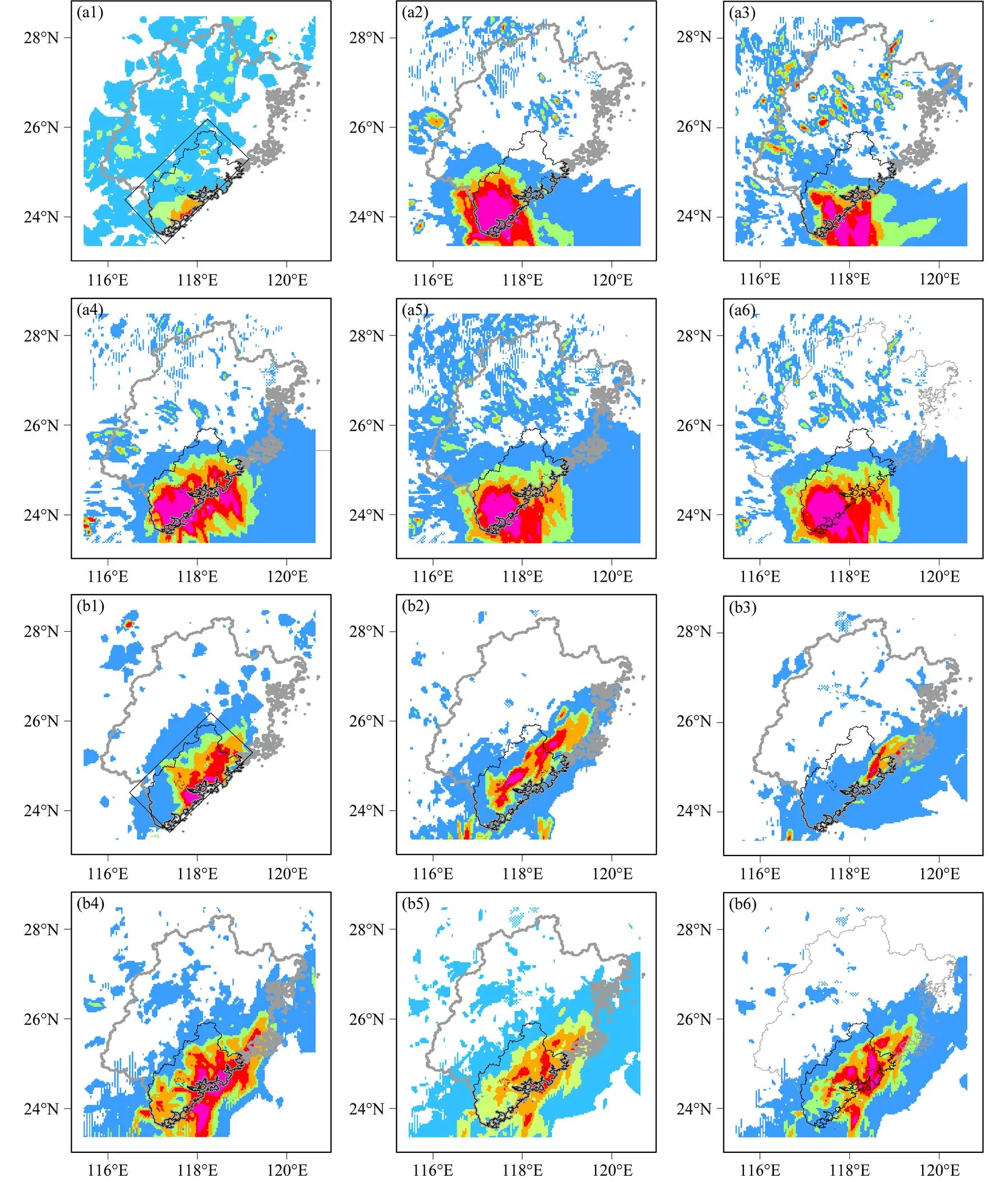
图8 （a1–a6）2013年7月18日00时至12时福建省累积降雨量；（b1–b6）2013年7月18日12时至19日00时福建省累积降雨量；（c1–c6）2013年7月19日00时至12时福建省累积降雨量。（a1、b1、c1）观测降雨量；（a2、b2、c2）“暖—潜热加热纳近”得到的降雨量；（a3、b3、c3）GRAPES_MESO模式得到的降雨量；（a4、b4、c4）基于九点平滑滤波的“暖—潜热加热纳近”得到的降雨量；（a5、b5、c5）简单集合平均得到的降雨量；（a6、b6、c6）概率匹配的降水集合。黑色矩形区域表示闽三角地区

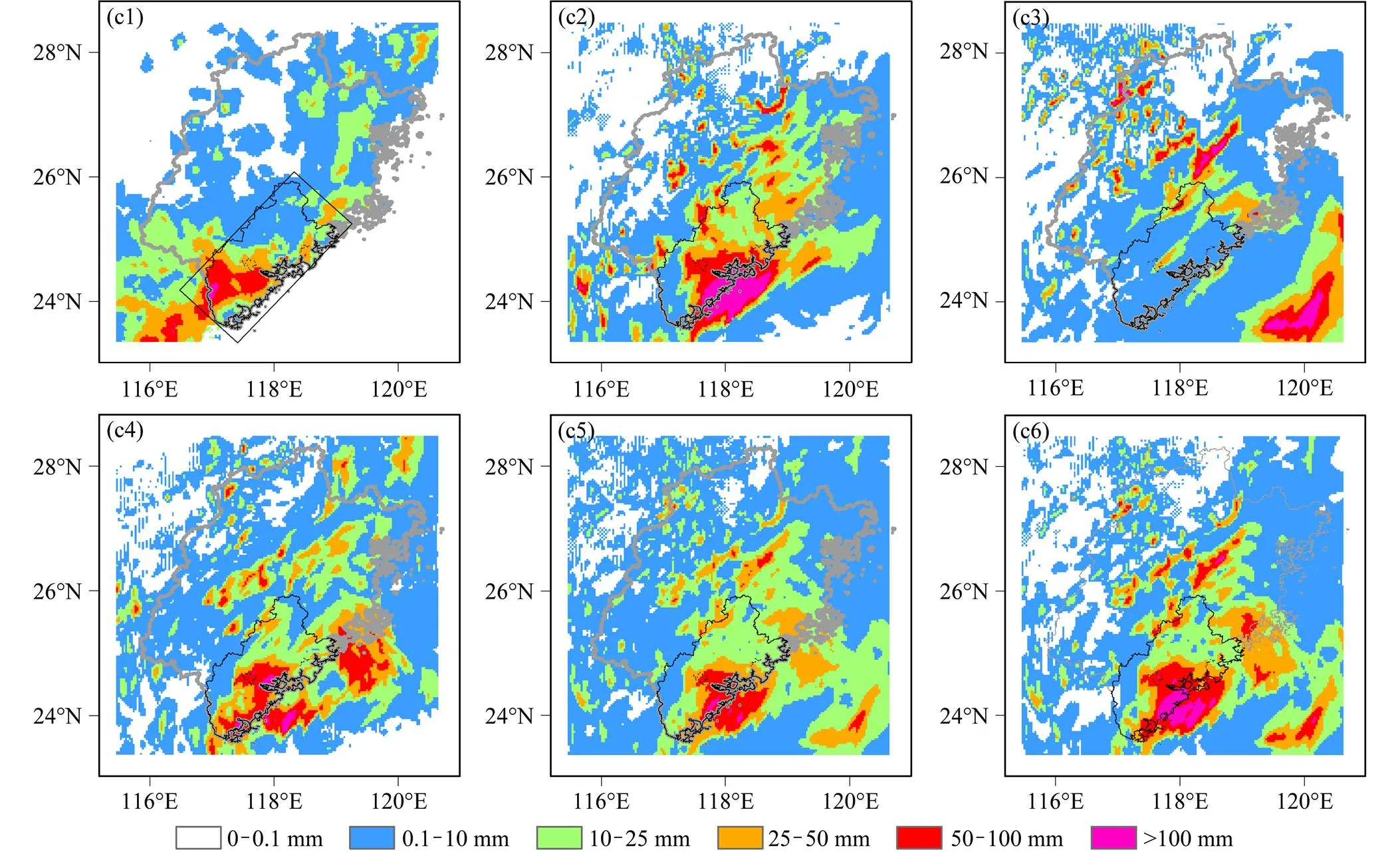
图8 （续）

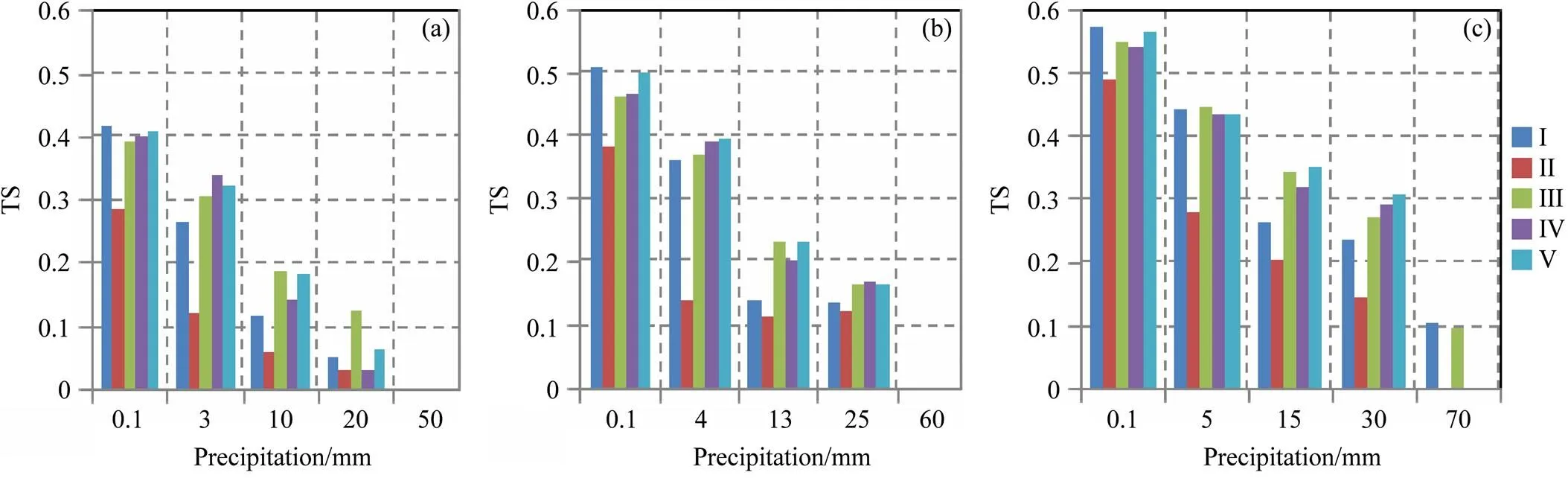
图9 2013年7月18日00时到19日12时（a）3小时、（b）6小时、（c）12小时累积降水TS评分。色标I、II、III、IV和V分别表示“暖—潜热加热纳近”、GRAPES_MESO模式、基于九点平滑滤波的“暖—潜热加热纳近”、简单集合平均和概率匹配的降水集合

从2013年7月18日00时至7月19日12时，利用GRAPES-Landslide集合预报模型进行预报时长为12 h，连续36 h的滚动预报。每一个30 m空间分辨率的研究单元，都要进行5×100组试验，得到500个预报的安全系数值。如果试验结果中有300个以上的安全系数值小于1，即该研究单元发生滑坡的概率大于60%，我们就认为该研究单元为滑坡危险点。为了使滑坡预报结果更加直观，我们进行了研究单元的聚合。将100×100个空间分辨率为30 m的研究单元聚合为一个空间分辨率为3000 m的小区域，统计这个小区域中滑坡危险点的数量。如果小区域内无危险点，则认为该小区域为安全区域；如果危险点在5个以下，则为滑坡少发区：如果危险点在5～50个之间，则该区域为多发区；如果危险点数大于50个，则为滑坡灾害频发区。

“西马仑”台风在闽三角地区诱发了大量的滑坡地质灾害，主要集中在漳州市，厦门市也有部分区域发生滑坡灾害，泉州市受到的影响较小。福建省地质环境监测中心收集的滑坡灾害点主要集中在漳州市的华安县、龙海市和云霄县（图10c中黑色框区域）。从图10中可以看到，实况的分布与本模型的预测结果比较接近，收集到的发生大密度滑坡的区域都集中在预报的滑坡频发区内。根据预报结果，在闽三角的东北部区域也有一些散落的滑坡频发区。根据新闻报道，在闽三角地区的东北部确实也出现了部分滑坡灾害。闽三角的中部有一个预报的滑坡频发区域，但是实际并没有大量的滑坡灾害发生，造成这种差异的原因是该区域的降雨预报结果偏大。2013年7月18日发布的全国地质灾害气象预警预报结果与本模型的结果较为一致，但是本模型的结果更能反映出滑坡的区域易发性差异，具有较大的滑坡灾害临近预报价值。福建国土资源厅2013年7月18日发布的地质灾害预警与实况和本文的预报结果都具有一定的偏差。在实际业务中，参考GRAPES-Landslide滑坡集合预报模型的预报结果，有助于提高预报的准确性。由于缺少精确的滑坡发生时间和地点的记录资料，无法对模型结果进行更为详细的验证。下一步的研究需要收集更为详尽的滑坡记录资料，以便更精确的评估模型模拟效果。

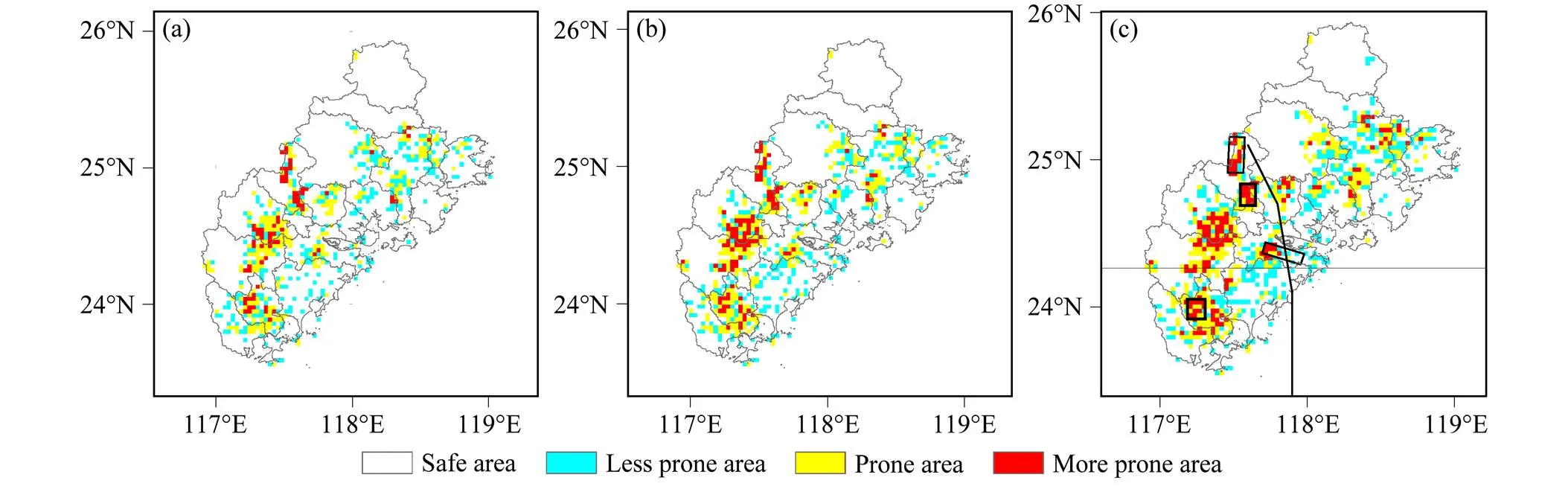
图10 （a）2013年7月18日00时至12时、（b）2013年7月18日12时至19日00时、（c）2013年7月19日00时至12时的闽三角地区滑坡灾害预警图。黑色框区域：观测到大量滑坡发生的区域；黑色线条：台风“西马仑”路径

5 结论与讨论

滑坡的实时预警系统GRAPES-Landslide是将数值天气预报模式GRAPES与滑坡预测模型TRIGRS进行单向耦合建立起来的动力数值预报预警系 统。由于滑坡预测模型TRIGRS中的关键水土参数具有空间分布很不均的特性，很难获取准确的数据加以描述，使得滑坡事件的激发、预测存在很大的不确定性，同时数值天气预报模式本身具有不确定性，因而用于诱发滑坡灾害的估测降水存在不确定性，进而使得滑坡的预报存在偏差。本研究基于预测降水和水土参数分布不确定性的考虑，提出了GRAPES-Landslide滑坡集合预报模型，建立在概率论基础上的可靠度被引入到边坡的稳定性评价中，使得滑坡的预报方法由确定性预报，改进为概率预报，预报结果更为科学和精确。

滑坡集合预报模型中有5个不同的预报降水成员，分别是（1）GRAPES_MESO业务模式、（2）“暖—潜热加热纳近”方法、（3）基于九点平滑滤波的“暖—潜热加热纳近”方法、（4）对（1）～（3）的降水成员进行简单平均、（5）对（1）～（3）的降水成员进行概率匹配的集合。根据水土参数呈正态分布的特点，通过Monte-Carlo方法随机生成100组扰动参数值。将5个预报降水与100组扰动水土参数结合，组成GRAPES-Landslide滑坡集合预报模型。本文选取了2013年7月台风“西马仑”降水在福建省诱发的系列滑坡案例进行模拟分析。降水预报结果表明，GRAPES业务预报模型的降水预报TS评分都显著低于其他四个降水成员，其他四个降水成员对小雨、中雨、大雨和暴雨的预报能力不同。利用不同的降水成员预报降水过程，可以减小降水预报的不确定性。初步的滑坡预报结果表明本文建立的GRAPES-Landslide滑坡集合预报系统所预测的滑坡频发区与观测区域有很好的吻合度，与目前的滑坡业务预报结果相比有明显改进，落区更精细化，对滑坡灾害的预测具有一定的指导意义。

由于缺乏详细的滑坡记录，无法对滑坡预测结果进行更为精确的验证。下一步要利用遥感图像，并配合实地勘探，整理出一套完整详尽的滑坡记录资料，进一步检验GRAPES-Landslide滑坡集合预报系统的预报能力。同时将模型由串行计算改为并行运算，提高模型运算速率，减少计算时间，为实现滑坡预报的业务化运行奠定基础。

（References）

Baecher G B, Christian J T. 2003. Reliability and Statistics in Geotechnical Engineering [M]. Hoboken: Wiley, 605pp.

Baum R L, Savage W Z, Godt J W. 2008. TRIGRS—A Fortran program for transient rainfall infiltration and grid-based regional slope-stability analysis, Version 2.0 [R]. USGS, Colorado, Open-File Report 2008–1159, 75pp.

Chen C Y, Chen T C, Yu F C, et al. 2005. Analysis of time-varying rainfall infiltration induced landslide [J]. Environ. Geology , 48 (4–5): 466–479.

Chen Yueli, Chen Dehui, Li Zechun, et al. 2016. Preliminary studies on the meticulous dynamic prediction method of rainfall-triggered landslide [J]. J. Mount. Sci., doi:10.1007/s11629-014-3110-5.

陈则佑, 冯正一, 庄育蓁. 2011. 应用TRIGRS程式于边坡破坏机率分析——以奥万大地区为例 [J]. 中华水土保持学报, 42 (3): 228–239. Chen T Y, Feng Z Y, Chuang Y C. 2011. An application of TRIGRS on slope failure probability analyses—A case study of Aowanda [J]. Journal of Chinese Soil and Water Conservation (in Chinese), 42 (3): 228–239.

Chowdhury R, Flentje P. 2003. Role of slope reliability analysis in landslide risk management [J]. Bull. Eng. Geology Environ., 62 (1): 41–46.

Chowdhury R, Flentje P, Bhattacharya G. 2010. Geotechnical Slope Analysis [M]. Boca Raton: The Chemical Rubber Company Press, 737pp.

丛威青, 李铁锋, 潘懋, 等. 2008. 基于非饱和渗流理论的区域降雨型地质灾害动力学预警方法研究 [J]. 北京大学学报, 44 (2): 212–216. Cong Weiqing, Li Tiefeng, Pan Mao, et al. 2008. Research on dynamic predictive model of regional rainfall-triggered geologic hazard based on unsaturated flow theory [J]. Acta Sci. Nat. Univ. Pekin. (in Chinese), 44 (2): 212–216.

Fairfield J, Leymarie P. 1991. Drainage networks from grid digital elevation models [J]. Water Resource Res., 27 (5): 709–717.

Godt J W, Baum R L, Savage W Z, et al. 2008. Transient deterministic shallow landslide modeling: Requirements for susceptibility and hazard assessments in a GIS framework [J]. Engin. Geology, 102 (3–4): 214–226.

Griffiths D V, Huang J S, Fenton G A. 2011. Probabilistic infinite slope analysis [J]. Comp. Geotechn., 38 (4): 577–584.

Park H J, Lee J H, Woo I. 2013. Assessment of rainfall-induced shallow landslide susceptibility using a GIS-based probabilistic approach [J]. Engin. Geology, 161 (18): 1–15.

Iverson R M. 2000. Landslide triggering by rain infiltration [J]. Water Resources Res., 36 (7): 1897–1910.

Kim D, Im S, Lee S H, et al. 2010. Predicting the rainfall-triggered landslides in a forested mountain region using TRIGRS model [J]. J. Mount. Sci., 7 (1): 83–91.

李媛, 孟晖, 董颖, 等. 2004. 中国地质灾害类型及其特征——基于全国县市地质灾害调查成果分析 [J]. 中国地质灾害与防治学报, 15 (2): 29–34. Li Yuan, Meng Hui, Dong Ying, et al. 2004. Main types and characteristics of geo-hazards in China—Based on the results of geo-hazard survey in 290 counties [J]. The Chinese Journal of Geological Hazard and Control (in Chinese), 15 (2): 29–34.

Liao Zonghu, Hong Yang, Wang Jun, et al. 2010. Prototyping an experimental early warning system for rainfall-induced landslides in Indonesia using satellite remote sensing and geospatial datasets [J]. Landslide, 7 (3): 317–324.

Liao Zonghu, Hong Yang, Kirschbaum Dalia, et al. 2011. Evaluation of TRIGRS (transient rainfall infiltration and grid-based regional slope- stability analysis)’s predictive skill for hurricane—Triggered landslides: A case study in Macon County , North Carolina [J]. Nat. Hazards, 58 (1): 325–339.

林蓬琪, 侯萍. 1990. 闽南三角地区花岗岩风化残积土斜坡结构特征及边坡稳定性分析 [J]. 福建地质, 9 (2): 146–156. Lin Pengqi, Hou Ping. 1990. Slope structure and slope stability of granitic weathering residual soil in south Fujian [J]. Geology of Fujian (in Chinese), 9 (2): 146–156.

Liu C N, Wu C C. 2008. Mapping susceptibility of rainfall-triggered shallow landslides using a probabilistic approach [J]. Environ. Geology, 55 (4): 907–915.

Lumb P. 1966. The variability of natural soils [J]. Canad. Geotechn. J., 3 (2): 74–96.

Park H J, Um J -G, Woo I, et al. 2012. Application of fuzzy set theory to evaluate the probability of failure in rock slopes [J]. Engin. Geology, 125: 92–101.

Vanmarcke E H. 1977. Probabilistic modeling of soil profiles [J]. Journal of the Geotechnical Engineering Division, 103 (11): 1227–1246.

Raia S, Alvioli M, Rossi M, et al. 2014. Improving predictive power of physically based rainfall-induced shallow landslide models: A probabilistic approach [J]. Geosci. Model Dev., 7: 495–514.

Varnes D J. 1978. Slope movement, types and processes [C]// Schuster R L, Krizek R J. Special Report 176: Landslides, Analysis and Control. Washington D. C.: Transportation and Road Research Board, National Academy of Science, 11–13.

Vieira B C, Fernandes N F, Filho O A. 2010. Shallow landslide prediction in the Serra do Mar, São Paulo, Brazil [J]. Nat. Hazards Earth Syst. Sci., 10: 1829–1837.

王清, 蒋惠忠, 唐大雄. 1990. 闽南三角地区花岗岩残积土及其工程地质特性的研究 [J]. 福建地质, 9 (2): 90–99. Wang Qing, Jiang Huizhong, Tang Daxiong. 1990. A study on engineering geological properties of granitic residual soil in south Fujian [J]. Geology of Fujian (in Chinese), 9 (2): 90–99.

Wang Y, Cao Z J, Au S K. 2010. Efficient Monte Carlo simulation of parameter sensitivity in probabilistic slope stability analysis [J]. Comput. Geotechn., 37 (7–8): 1015–1022.

魏丽. 2005. 暴雨型滑坡灾害形成机理及预测方法研究 [D]. 南京信息工程大学博士学位论文. Wei Li. 2005. Study on mechanism and predicting method of landslide hazard triggered by extremely heavy rainfall [D]. Ph. D. dissertation (in Chinese), Nanjing University of Information Science & Technology.

吴亚丽, 陈德辉. 2015. 潜热加热纳近方法在地面降水资料同化中的应用 [J]. 应用气象学报, 26 (1): 32–44. WuYali, Chen Dehui. 2015. Application of latent heat nudging method to assimilating surface precipitation observation [J]. J. Appl. Meteor. Sci. (in Chinese), 26 (1): 32–44.

肖玉华, 何光碧, 陈静, 等. 2011. 区域集合预报增长模繁殖扰动方法研究 [J]. 高原气象, 30 (1): 94–102. Xiao Yuhua, He Guangbi, Chen Jing, et al. 2011. Study on perturbing method in regional BGM ensemble prediction system [J]. Plateau Meteor. (in Chinese), 30 (1): 94–102.

Zhang Renhe, Shen Xueshun. 2008. On the development of the GRAPES— A new generation of the national operational NWP system in China [J]. Chinese Sci. Bull., 53 (22): 3429–3432.

An Ensemble Prediction Model for Rainfall-Induced Landslides and Its Preliminary Application

CHEN Yueli1, 2, 3, CHEN Dehui3, LI Zechun4, WU Yali5, and HUANG Junbao6

1,,210044,2,,100081,3,,100081,4,100081,5,,,510080 ,6,350002

The rainfall-triggered landslide disaster early warning model GRAPES-Landslide is a physical deterministic model that couples the GRAPES model (Global/Regional Assimilation and PrEdiction System) and the TRIGRS model (Transient Rainfall Infiltration and Grid-based Regional Slope-stability). The input parameters, such as cohesion and friction angle, used in the TRIGRS model have been identified as a major source of uncertainty, because of their spatial variability. Such uncertainty of numerical weather prediction also has an impact on landslide forecasting. The authors propose an ensemble GRAPES-Landslide model for landslide prediction, taking into consideration the uncertainty of the input parameters and rainfall prediction. There are five rainfall predicting members in the ensemble model including the GRAPES model, the warm latent heat nudging method, the warm latent heat nudging method with a nine-point moving average filter, the simple averaging method of the first three members, and the averaging method of the probability matching of the first three members. Using the cumulative distribution for each random variable and a random number generator, 100 sets of parameter values were randomly generated. The ensemble model was applied to forecast the landslide occurrences in Min-San-Jiao, Fujian Province, during a typhoon rainfall process in 2013. Results showed that the observed landslide areas were located in the high risk areas. Compared with the operational landslide forecasting, the prediction result of the ensemble GRAPES-Landslide model was more accurate. The ensemble GRAPES-Landslide model provides a new probability prediction method for landslides.

Rainfall-induced landslides, GRAPES-Landslide model, Ensemble prediction

10.3878/j.issn.1006-9895.1503.15120.

1006-9895(2016)03-0515-13

P456

A

10.3878/j.issn.1006-9895.1503.15120

2015-01-29；网络预出版日期 2015-03-27

陈悦丽，女，1985年出生，博士，主要从事灾害的预报预警技术研究。E-mail: chenyl@camscma.cn

陈德辉，E-mail: chendh@cma.gov.cn

国家重点基础研究发展计划（973计划）项目2013CB430106，国家自然科学基金项目41375108

Funded by National Basic Research Programs of China (973 Program) (Grant 2013CB430106), National Natural Science Foundation of China (Grant 41375108)

陈悦丽, 陈德辉, 李泽椿，等. 2016. 降雨型滑坡的集合预报模型及其初步应用的试验研究 [J]. 大气科学, 40 (3): 515–527. Chen Yueli, Chen Dehui, Li Zechun, et al. 2016. An ensemble prediction model for rainfall-induced landslides and its preliminary application [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 40 (3): 515–527,