对未来两个太阳周太阳活动参数的统计预测
2016-10-10丁煌廖云琛肖子牛
丁煌廖云琛肖子牛,
(1 中国电力科学研究院,南京 210003; 2 南京信息工程大学,南京 210044;3 中国科学院大气物理研究所,北京 100029)
对未来两个太阳周太阳活动参数的统计预测
丁煌1廖云琛2肖子牛2,3
(1 中国电力科学研究院,南京 210003; 2 南京信息工程大学,南京 210044;3 中国科学院大气物理研究所,北京 100029)
利用支持向量机(Support Vector Machine,SVM)和后向传播(Back Propagation,BP)神经网络的方法,结合前23个太阳周期(1700—2008年)的周期特征数据,对第24和第25个太阳周的各个周期特征进行了预测,并且通过交叉验证算法得出两种方法都可达到最优。通过分析SVM与BP神经网络方法的预测结果,均表明第25个太阳周将会达到较强的强度,且大于第24个太阳周。此外,两种方法都预测出第25个太阳周的太阳黑子数在谷值年维持异常偏低,周期长度都会维持在10年左右。根据第24个太阳周已经过去的特征验证,BP神经网络的结果与实际情况更为接近,预测太阳活动在2020开始进入第25个太阳周,在2025年达到峰值,峰值年强度比第24个太阳周偏强。
太阳黑子数,太阳周期,支持向量机,后向传播神经网络
0 引言
众所周知,太阳辐射变化对地球气候的形成和长期演变有着重要的影响[1]。IPCC报告[2]指出,太阳直接辐射对气候变化的影响虽然很小,但太阳活动的影响有可能在气候系统相互作用的某些环节存在调制作用,使得太阳对气候的影响超过人们的想象。Stauning[3]利用太阳周平均的黑子数代表太阳活动的强弱,发现全球温度的变化与太阳活动的水平有联系。事实上,许多研究也指出太阳活动对地球气候系统有一定的影响[4-8]。基于观测和数值模式试验的众多研究分析结果也揭示出地球上有许多区域存在对太阳变化和周期信号的显著响应[9]。Misios等[10]指出,太阳活动高值年,赤道西太平洋的深对流区向东移动;Meehl等[5]指出在太阳峰值年,整个热带太平洋地区会出现类冷事件,而峰值年之后一至两年,会出现类暖事件。屠其璞等[11]在分析了太阳黑子活动与中国极端事件的关系后发现,太阳黑子活动极大值年附近我国旱、涝事件出现频率呈现显著增加趋势;Zhao等[12-13]确认了东亚夏季风爆发期季风区雨带纬度位置年代际变化在一定程度上与太阳黑子周期位相有关。1991年,Friis-Christensen等[14]的研究发现,每个太阳周的时间长度和全球地表温度有密切的联系。最近,Maliniemi等[15]指出,北半球的冬季气温异常型在太阳周的不同相位(谷值期、上升期、峰值期和下降期)有显著的差异,尤其在下降时期有明显的一致性特征。这些结果说明,太阳活动在一个太阳周内可以表现为周期强度、周期长度、上升年份、下降年份、峰值和谷值等不同的特征,而这些特征的变化都会对地球的气候产生一定的影响。因此,对这些特征的预测对于预估未来地球气候的变化具有重要的意义。对未来太阳周的预测,一直是人们关注的问题,迄今为止还没有物理上明确的预测方法,主要以统计方法对周期的强度和峰值的出现时间进行预测[16-21]。本文利用支持向量机(Support Vector Machine,SVM)和后向传播(Back Propagation,BP)神经网络的方法,结合前23个太阳周期(1700—2008年)的周期特征(周期长度、周期平均黑子数、周期峰值黑子数、周期谷值黑子数、上升年数(不包含峰值年)、下降年数(不包含谷值年))数据,对第24和第25个太阳周的各个周期特征进行了预测。本文在后文中介绍了使用的方法以及资料,并且给出了预测结果。
1 资料与方法
1.1太阳黑子资料
使用太阳影响数据分析中心(SIDC)所提供的逐年平均太阳黑子数资料计算了1700—2008年共23个太阳周期(一个太阳周期定义为谷值年到下一个谷值年的时间长度(不包含后一个谷值年))的周期特性,包括:周期长度、周期平均黑子数、周期峰值黑子数、周期谷值黑子数、上升年数(不包含峰值年)、下降年数(不包含谷值年)。接下来,我们将使用SVM以及BP神经网络来预测第24和第25个太阳周的以上周期特性。并按照周期特性来还原出第24和第25个太阳周的太阳黑子数的时间序列。
1.2支持向量机
SVM是一种建立在统计学习理论的VC维理论和结构风险最小原理基础上的,在解决小样本、非线性及高维模式识别中能够表现出许多特有的优势,并能够推广应用到函数拟合等其他机器学习问题中的方法[22]。其基本思想是通过用内积函数定义的非线性变换将输入空间变换到一个高维空间,在这个高维空间中寻找输入变量和输出变量之间的一种非线性关系[23-26]。这样在高维特征空间的线性回归就对应于低维输入空间的非线性回归,也使得计算的复杂度不再取决于空间维数,而是取决于支持向量的个数。
根据以上理论可知支持向量机的回归就是为了寻找一个f(x)=ω·x+b,使其结构风险最小化。有样本数据((xi, yi),i=1, 2, 3…, n),xi∈Rd为输入,yi∈R为对应输出,d为输入维数,n为样本总数,假定存在函数f在ε精度能够估计所有的(xi, yi)数据,寻找回归函数可由以下最优化问题转化:
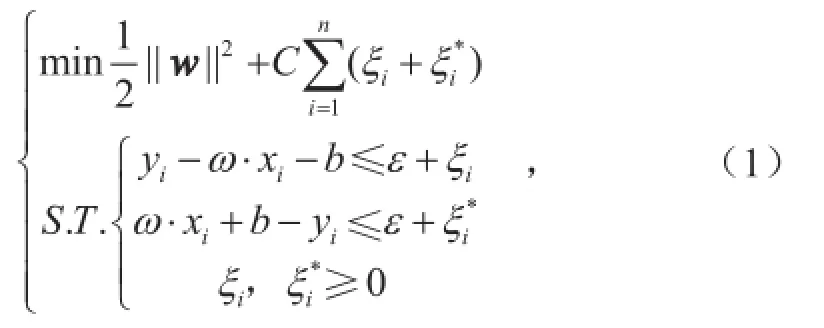
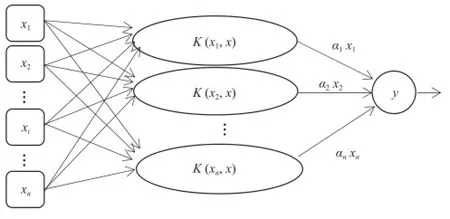
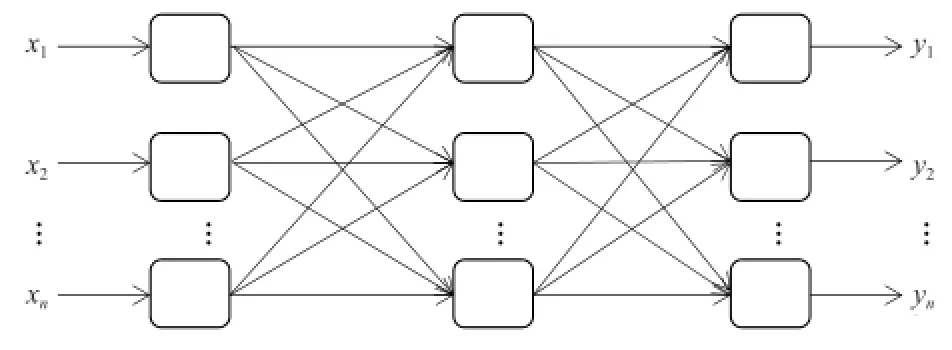
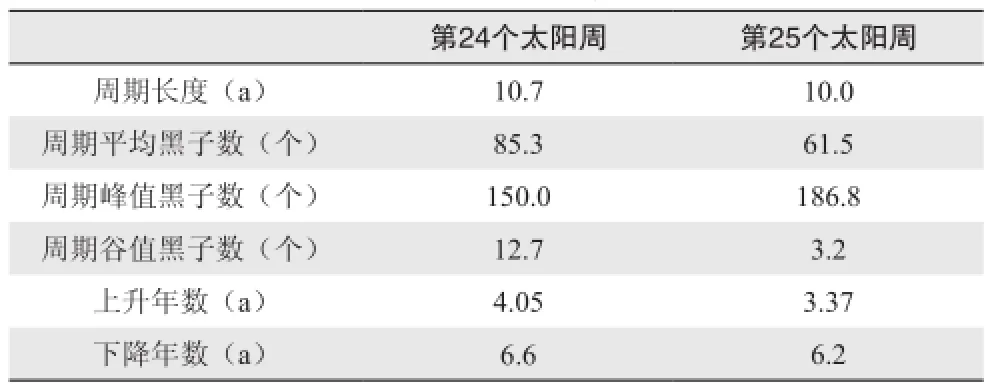
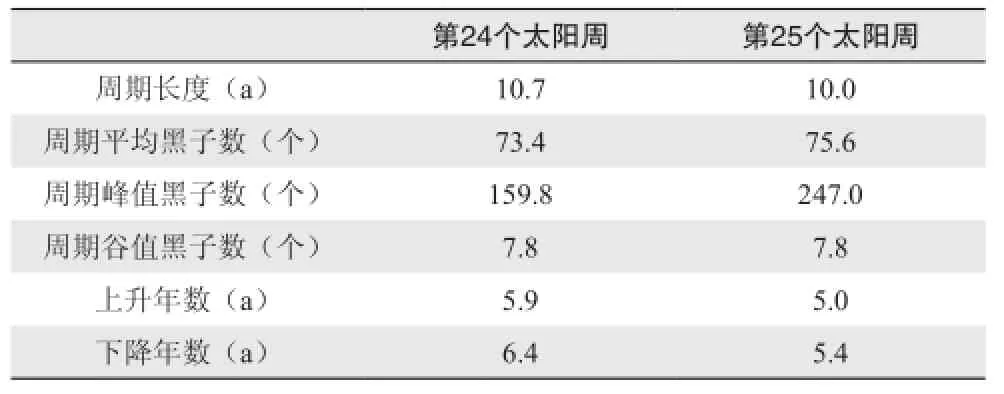
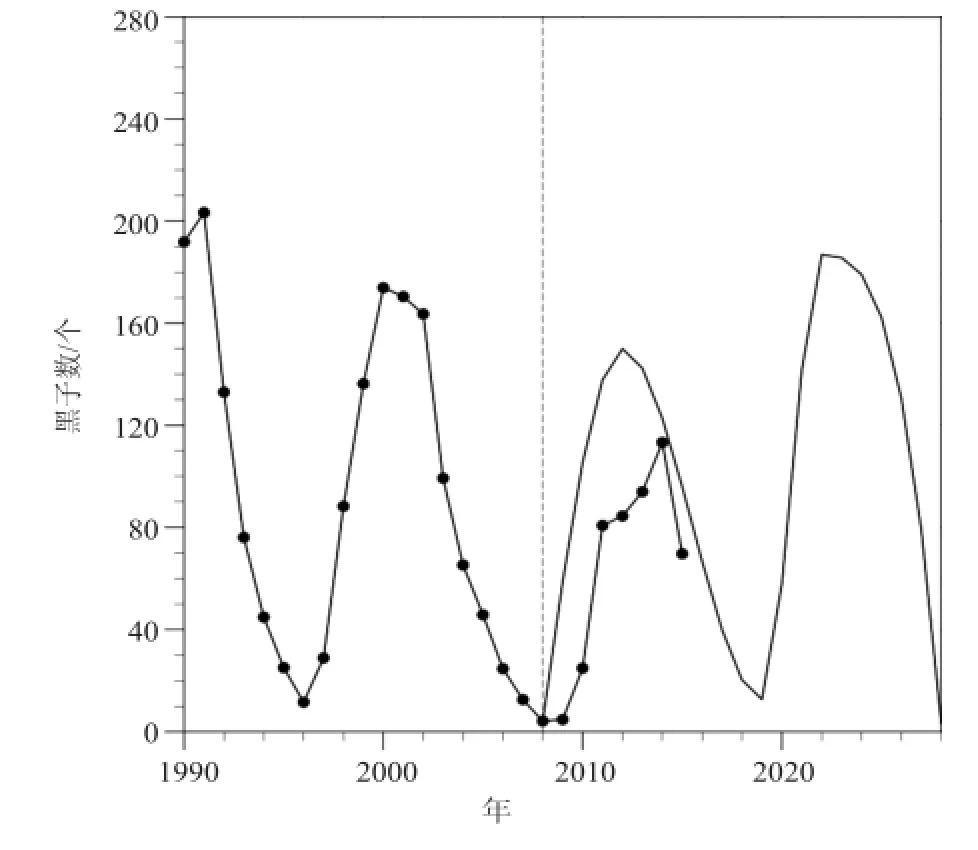
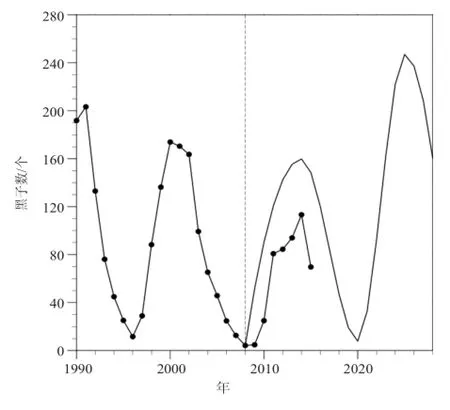
上式中w为回归函数法向量;ε为损失函数,表示函数拟合精度;为松弛变量,可以放宽函数优化条件;常数C>0控制对训练误差超出误差带ε样本的惩罚程度,即为惩罚系数。通过引入拉格朗日乘子αi和αi*(0<αi,αi* 满足Mercer条件[26]的任何对称的核函数都对应于特征空间的点积。核函数的引入,避免了对显式非线性映射Φ的寻找。有许多种核函数都满足此条件,如多项式核函数、径向基核函数和柯西核函数等。其中径向基核函数(式3)因其优秀的局部逼近特性在SVM中应用最为广泛,它利用局部接受域完成函数映射:只有当输入落入输入空间的一个局部区域时,基函数才产生一个重要的非零响应,而其他情况下的响应近似为零。文中采用核函数即为径向基核函数。SVM回归结构与一个三层前馈神经网络相似:其中输入层基本相同,隐含层节点对应于一个输入样本与一个支持向量的内积核函数,输出层节点对应于隐含层输出的线性组合。图1为支持向量机回归原理示意图。 图1 支持向量机示意图Fig. 1 Schematic diagram of SVM 1.3后向传播神经网络 后向传播算法[28]的特点是信号的前向计算与误差的反向传播。信号前向计算时,输入样本首先由输入层传入,经过各隐含层(一层或多层)逐层传输并处理后,最后传向输出层,由该层输出。在此过程中若是最后由输出层输出的实际值与期望值不符,则转入误差的方向传播阶段。误差反向传播可以简单理解为将误差作为输入传入各层不断调整权值以达到修正的目的。具体做法是将误差通过输出层,按误差梯度下降的方式通过隐含层向输入层逐层反传,并调整各层权值。信号前向计算与误差反向传播不断进行,既是权值不断调整的过程亦是网络训练过程,调整权值的原则是使误差不断地减小。此过程一直持续到网络输出的误差减少到初始设定参数的程度抑或到达最大训练次数。 图2[29]是一个典型的三层BP神经网络,只有一个隐含层,也可以根据实际情况适当增加隐含层层数。一般使用双极性Sigmoid函数: 作为激发函数。由图可见BP神经网络包括三层,从左到右分别是输入层、隐含层和输出层,若有样本数据((Pi, Ti), i=1, 2, 3,…, n),则其中的Pi作为输入向量。首先赋予各权值的初始值,即输入层至隐含层的连接权ωij(i=1, 2,…, n;j=1, 2,…, p)、隐含层至输出层的连接权vjt(j=1, 2 ,…, p;t=1, 2,…, q)、隐含层各单元的输出阈值θj(j=1, 2,…, p)和输出层各单元的输出阈值γt(t=1, 2,…, q)赋予区间(-1, 1)内的随机值。之后网络随机选取一组输入样本和目标样本提供计算。有了上述样本等值就可以计算中间隔层单元的输入sj,它需要有输入样本Pk、连接权ωi和阈值θj,计算好以后将sj通过传递函数来算出隐含层各单元的输出bj。其中, 接着计算输出层各单元的输出Lt,过程跟sj类似,需要用到隐含层的输出bj、连接权vjt和阈值γt,然后通过传递函数计算输出层各单元的实际输出Ct。其中, 然后可以通过以上条件结合下式获得输出层的各单元一般化误差: 由式(9)可知,需要通过网络目标向量和网络的实际输出计算得出。此时进入了误差反传的阶段,有了输出层的一般化误差,再结合连接权vjt和隐含层的输出bj共同得到隐含层各单元的一般化误差: 现在有了各层误差,即可以通过误差来修正各连接权和阈值。先根据(11)、(12)两式,将输出层各单元的一般化误差与隐含层各单元的输出bj来修正连接权vjt和阈值γt: 其中,。再利用(13)和(14)两式来修正连接权ωij和阈值θj,此过程需要用到隐含层各单元的一般化误差和输入层个单元的输入。 式中,。此时一次训练已经完毕,接下来随机选取下一个训练样本向量提供给网络,返回向量输入开始初始运算,反复训练直到满足规定误差范围内,即网络收敛。若是学习次数大于最大训练次数,网络则无法收敛。无论网络收敛与否,运行到此时整个网络学习都将结束。 图2 BP神经网络示意图Fig. 2 Schematic diagram of BP neural network method 1.4交叉验证算法及过程 采用交叉验证的思想可以在某种意义下得到最优的建模参数,可以有效地避免过学习和前学习状态的发生,最终能够在有效样本的情况下得到较理想的预报值。 所谓交叉验证的基本思想是在一定意义下,将原始样本进行分组,一部分作为训练样本,另一部分作为检验样本。大致方法是,首先利用训练样本对模型进行训练,然后利用检验样本来检验由训练样本训练好的模型,以预报准确率作为检验该模型效果的指标。本文利用K次交叉验证(K-Fold Cross Validation),将初始样本分割成K个子样本,选取K个子样本中的一个单独的子样本用作检验模型,而其他(K-1)个子样本用作训练模型。该交叉验证需要重复K次,被分的每个子样本都需要检验一次,最后平均K次的结果得到最后结果。随机产生的子样本能够被同时重复利用于训练和检验是该方法的最大优势。将每次的结果检验一次,也不是次数越多越好,要根据具体情况具体采用。试验结果表明使用K次交叉验证能够更好地寻找到建模最优参数。 在建模选择参数时使用到了10次交叉验证,具体做法是在训练预报模型前,随机将样本数据集切割成10个子样本,顺序抽取一个子样本为检验样本,其他9个则作为训练样本来训练模型,训练完毕后使用选取出的检验样本验证该模型,如此循环。最后综合对10个子样本验证的结果,选取最优参数和最优模型,使结果更好。 1.5建模 在建模中,为了消除数据对模型的影响,所有带入模型中的数据都需要进行归一化处理,处理方法为x=(xi-m)/(M-m),其中xi为因子的实际值,x为归一化后的值,M和m分别为该因子所有取值中的最大值和最小值。本文利用SVM对逐周期太阳周期特征(周期长度、周期平均黑子数、周期峰值黑子数、周期谷值黑子数、上升年数(不包含峰值年)和下降年数(不包含谷值年))数据进行预测,最优训练数据个数为5个。 建模之前,进行了部分敏感性试验。由于数据是一组时间序列,考虑到训练数据个数和训练参数的选取对模型建立影响较大,故将数据分成前3个数据为训练、1个数据为检验;4个数据为训练、1个数据为检验;5个数据为训练、1个数据为检验,…,14个数据为训练、1个数据为检验,利用交叉验证算法得到逐周期太阳周期特征的几个数据集,利用5个数据作为训练都能得到最优。 通过使用SVM与BP神经网络方法,得到了第24和第25个太阳周的各个周期特征(周期长度、周期平均黑子数、周期峰值黑子数、周期谷值黑子数、上升年数(不包含峰值年)和下降年数(不包含谷值年))。通过交叉验证算法发现结果都能得到最优。可见,两种预测模型都比较有效,其预测结果分别如表1和表2所示。BP神经网络得到的第25个太阳周的强度弱于SVM的结果。此外,两种方法都预测出第25个周期的太阳黑子数谷值较往年低。两种方法的周期长度预测结果表明,第24和第25个太阳周的周期长度较短,都少于11年。同时,SVM预测的第24和第25个太阳周的上升年数较短,仅仅维持3~4年。第25个太阳周虽然在峰值年太阳黑子数较多,可以达到187个,但其低谷年太阳活动异常平静,在整个第25个太阳周中,年平均太阳黑子数仅为61.5个,太阳活动整体看仍然维持较低的水平。BP神经网络预测结果整体类似,第24和第25个太阳周上升年数分别为5.9和5.0a,下降年数分别为6.4和5.4a。第24和第25个太阳周在峰值年太阳黑子数均较多,其中在第25个太阳周达到247个,谷年太阳活动均比较弱,太阳黑子数不到10个,在第24和第25个太阳周,年平均太阳黑子数分别为73.4和75.6个。 表1 使用SVM方法预测的第24和第25个太阳周的各个周期特征Table 1 The 24thand 25thsolar cycles' periodic characteristics predicted by SVM method 表2 使用BP神经网络方法预测的第24和第25个太阳周的各个周期特征Table 2 The 24thand 25thsolar cycles' periodic characteristics predicted by BP neural network method 图3 使用SVM方法预测的逐年太阳黑子数序列(虚线后为预测的第24—25周期,标有实心圆的实线为实际太阳黑子数序列)Fig. 3 The time series of sunspot number predicted by SVM method (The predicted 24thand 25thsolar cycles are after the dotted line, and the solid line with filled circle is the actual time series of sunspot number) 通过对第24和第25个太阳周预测得到的周期特征的条件限制,再通过插值可以方便地重构第24—25周的太阳黑子数的时间序列。图3和图4给出了1990—2015年实际太阳黑子数的变化曲线(标有实心圆的实线)以及2008年后使用两种方法预测的第24—25周的太阳黑子数的时间序列(虚线之后)。从图3可以看到,SVM方法预测的第24个太阳周在2012年达到峰值,并在2019年触及太阳活动谷底,开始进入第25个太阳周。第25个太阳周预计在2022年达到峰值,其强度会超过第24个太阳周的峰值强度。而从实际的2008—2015年的太阳黑子数序列上可以看出,第24个太阳周是在2014年达到峰值,其上升年数较SVM方法预测要多,整个周期较为推后。基于BP神经网络方法的预测中,第24个太阳周在2014年达到峰值,在2020年进入谷底且开始第25个太阳周,并预计在2025年达到峰值。BP神经网络预测的峰值年与实际情况一致,都位于2014年。此外,SVM与BP神经网络方法的预测结果都表明第25个太阳周未来达到峰值的强度将大于第24个太阳周,而第24个太阳周的峰值较第23个太阳周弱,这与实际太阳黑子数的序列比较一致。通过BP神经网络得到的预测结果与Schatten[30]的结果较为一致,都表明在2020年将会开始第25个太阳周。苗娟等[21]也指出,预计第25个太阳周从2020年开始,其强度与第23个太阳周类似,比第24个太阳周强。通过计算得出2009—2015年实际太阳黑子数与2009—2015年预测(SVM、BP神经网络)太阳黑子数的相关系数,结果如表3所示。BP神经网络得到的预测结果与实际太阳黑子序列的相关系数更高,通过了0.01的信度检验。因此,从已经过去的第24个太阳周的情况来看,BP神经网络方法的预测结果更接近实际情况。 表3 2009—2015年实际太阳黑子数(SSN)与2009—2015年预测(SVM,BP神经网络)太阳黑子数(SSN)的相关系数Table 3 The correlation coefficients between the 2009-2015 actual sunspot number (SSN) and the 2009-2015 predicted (SVM, BP neural network) SSN 图4 使用BP神经网络预测的逐年太阳黑子数序列(虚线后为预测的第24—25周期,标有实心圆的实线为实际太阳黑子数序列)Fig. 4 The time series of sunspot number predicted by BP neural network method (The predicted 24thand 25thsolar cycles are after the dotted line, and the solid line with filled circle is the actual time series of sunspot number) 本文基于SVM和BP神经网络方法对未来第24和第25个太阳周的主要周期特征进行了预测,结果表明两种方法都对太阳活动的演变趋势具有一定的预报能力,其中BP神经网络方法更为接近实际情况。未来预计在2020开始进入第25个太阳周,其上升时间较短,2025年达到峰值,且其峰值年强度比第24个太阳周要强。 [1]赵亮, 徐影, 王劲松, 等. 太阳活动对近百年气候变化的影响研究进展. 气象科技进展, 2011, 1(4): 37-48. [2]IPCC. IPCC Fourth Assessment Report: Climate Change 2007(AR4). IPCC, 2007. [3]Stauning P. Solar activity-climate relations: a different approach. J Atmos Solar-Terrestrial Phys, 2011, 73(13): 1999-2012. [4]Haigh J D. Te impact of solar variability on climate. Science, 1996,272(5264): 981-984. [5]Meehl G A, Arblaster J M. A lagged warm event-like response to peaks in solar forcing in the Pacific region. J Climate, 2009, 22(13): 3647-3660. [6]Gray L J, Beer J, Geller M, et al. Solar influences on climate. Rev Geophys, 2010, 48(4): 1032-1047. [7]Roy I, Haigh J D. Solar cycle signals in sea level pressure and sea surface temperature. Atmos Chemi and Phys, 2010, 10(6):3147-3153. [8]Bal S, Schimanke S, Spangehl T, et al. On the robustness of the solar cycle signal in the Pacific region. Geophysical Research Letters,2011, 38(14): 130-137. [9]肖子牛, 钟琦, 尹志强, 等.太阳活动年代际变化对现代气候影响的研究进展. 地球科学进展, 2013, 28(12): 1335-1348. [10]Misios S, Schmidt H. Mechanisms involved in the amplification of the 11-yr solar cycle signal in the tropical Pacific Ocean. J Climate,2012, 25(14): 5102-5118. [11]屠其璞. 近百年来我国降水量的变化. 南京气象学院学报, 1987,10(2): 177-187. [12]Zhao L, Wang J S, Zhao H J. Signature of the solar cycle on decadal variability in monsoon precipitation over China. J Meteor Soc Japan, 2012, 90: 1-9. [13]Zhao L, Wang J S. Robust response of the East Asian monsoon rainband to solar variability. J Climate, 2014, 27(8): 3043-3051. [14]Friis-Christensen E, Lassen K. Length of the solar cycle: an indicator of solar activity closely associated with climate. Science,1991, 254(5032): 698-700. [15]Maliniemi V, Asikainen T, Mursula K. Spatial distribution of Northern Hemisphere winter temperatures during different phases of the solar cycle. J Geophys Res (Atmospheres), 2014, 119(16):9752-9764. [16]王家龙. 第 22 和 23 太阳周太阳活动预测. 天体物理学报, 1992,12(4): 369-373. [17]王家龙. 相似周方法对第23周黑子数预测的检验. 第十届全国日地空间物理学术讨论会, 2003. [18]Wang J L, Gong J C, Liu S Q, et al. Te prediction of maximum amplitudes of solar cycles and the maximum amplitude of solar cycle 24. Chinese J Astro Astrophys, 2002, 2(6): 557. [19]柳士俊, 俞小鼎, 陈永义. 太阳黑子活动的守恒量预报. 科学通报, 2003, 48(17): 1832-1835. [20]Du Z L, Wang H N, Zhang L Y. A running average method for predicting the size and length of a solar cycle. Chinese J Astro Astrophys, 2008, 8(4): 477. [21]苗娟, 龚建村, 李志涛, 等. 第 25 太阳周太阳黑子数峰值预测. 中国科学(物理学, 力学, 天文学), 2015 (9): 95-101. [22]丁煌, 陶树旺, 肖子牛, 等. 基于WRF和SVM方法的风电场功率预报技术研究. 高原气象, 2013, 32(2): 581-587. [23]王定成, 方廷健, 唐毅, 等. 支持向量机回归理论与控制的综述.模式识别与人工智能, 2003, 16(2): 192-197. [24]冯汉中, 徐会明, 徐琳娜. SVM方法与长江上游降水落区预报.高原气象, 2004, 23(1): 63-68. [25]张学工. 关于统计学习理论与支持向量机. 自动化学报, 2000,26(1): 32-42. [26]Trevor H, Robert T, Jerome F. 统计学习基. 范明,柴玉梅,昝红英,译. 北京: 电子工业出版社, 2003. [27]Janjic Z, Black T, Pyle M, et al. High resolution applications of the WRF NMM. 21st Conf on Weather Analysis and Forecasting/17th Conf on Numerical Weather Prediction, 1-5 August 2005, Washington DC, Amer Meteor Soc. [28]韩爽. 风电场功率短期预测方法研究. 北京: 华北电力大学,2008. [29]傅荟璇, 赵红. MATLAB神经网络应用设计. 机械工业出版社,2010. [30]Schatten K. Fair space weather for solar cycle 24. Geophysical Research Letters, 2005, 32(21): 365-370. The Statistical Prediction of Sunspot Number for the Next Two Solar Cycles Ding Huang1, Liao Yunchen2, Xiao Ziniu2,3 In this work, the 24thand 25thsolar cycles' periodic characteristics were predicted by using support vector machine(SVM) method and back propagation (BP) neural network method respectively, based upon the data of previous 23 solar cycles. The authors found that both of the methods reach the optimal value after applying the cross validation algorithm, it reveals that the intensity of solar activity in the 25thsolar cycle will be enhanced comparing with the 24thsolar cycle in both the SVM and the BP Neural Network prediction; that the sun spot number (SSN) will maintain low value in the valley phase; and the cycle length will be around 10 years in the 25thsolar cycle. According to the periodic characteristics of the 24thsolar cycle that was past, there sults from BP Neural Network method prediction are more close to actual situation than that from the SVM. The results indicate that solar activity will enter 25thsolar cycle in 2020, and will reach the peak in 2025; the amplitude of peak year in the 25thsolar cycle will be stronger than that in the 24thsolar cycle. sun spot number, solar cycle, support vector machine, back propagation neural network 10.3969/j.issn.2095-1973.2016.04.003 2016年2月18日; 2016年3月23日 丁煌(1988—),Email: dinghuang@epri.sgcc.com.cn 肖子牛(1965—),Email: xiaozn@lasg.iap.ac.cn 资助信息:国家重大科学研究计划(2012CB957804)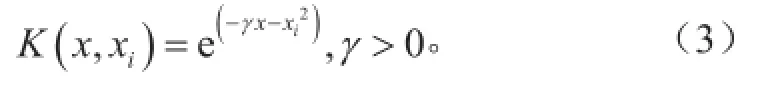

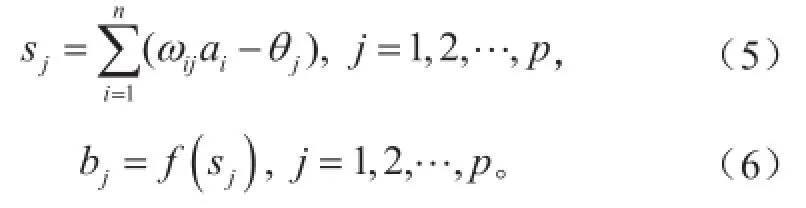

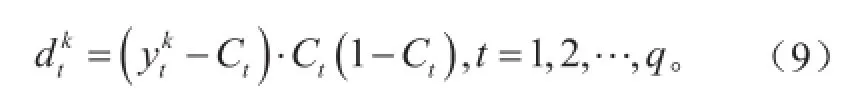
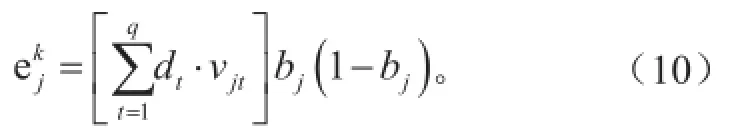
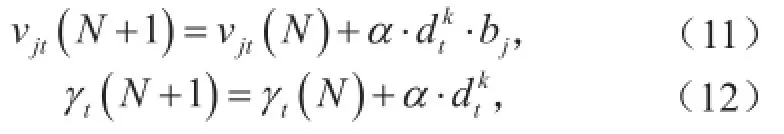

2 结果

3 总结
(1 China Electric Power Research Institute, Nanjing 210003 2 Nanjing University of Information Science and Technology, Nanjing 210044 3 Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029)
