采用玻尔兹曼统计法分析光阱刚度的测量精度

朱春丽，李　静

(中国科学技术大学 精密机械与精密仪器系，安徽 合肥 230027)



采用玻尔兹曼统计法分析光阱刚度的测量精度

朱春丽，李静*

(中国科学技术大学 精密机械与精密仪器系，安徽 合肥 230027)

考虑高精度的光阱刚度测量是光阱力测量的关键，本文提出了采用玻尔兹曼统计法来分析光阱刚度的测量精度。首先，描述了实验室搭建的近红外光镊系统，并将其搭建在暗室中的气垫平台上，以便隔离光干扰和振动干扰。然后，用四象限光电探测器探测被光镊捕获的微球向后散射的光，并选用与溶液黏度无关的玻尔兹曼统计法计算样品池底面附近的光阱刚度。最后,分析和讨论了溶液温度的变化、四象限光电探测器的灵敏度、采样频率以及采样时间对光阱刚度测量精度的影响。理论分析及实验计算显示：溶液温度的变化对光阱刚度的测量影响很小，但四象限光电探测器的灵敏度对光阱刚度测量精度影响较大。考虑采样的完整性和数据处理速度，采样频率通常取为被捕获颗粒拐角频率的5～10倍。对于本文搭建的近红外光镊测量系统，采样时间取为1～7 s时，可以保证高精度地测量光阱刚度。

光镊；近红外光镊系统；光阱刚度测量；玻尔兹曼统计法

*Correspondingauthor,E-mail:lijing@ustc.edu.cn

1　引　言

1986年，Ashkin等人首次报导了光镊技术[1]，之后光镊技术便被大量地运用于物理和生物学领域中，例如微观颗粒的操纵、分类和构型[2-4]，胶体物理的研究[5]以及在单分子水平对生物分子的研究[6]等。在这些应用中，通常需要测量光镊施加在微粒或生物分子上的光阱力。在光镊系统中，光镊施加在颗粒上的光阱力等于测量出的光阱刚度乘以被捕获颗粒相对于光阱中心的位移。通常用相机[7]和四象限光电探测器[8]测量被捕获颗粒的位移，可以达到纳米级精度。比较常用的几种光阱刚度的测量方法有流体力学法[9]、外加周期力法[10]、功率谱法[11]、能量均分法[12]和玻尔兹曼统计法[12]。其中，能量均分法简单、快速，但计算精度不高。流体力学法、外加周期力法和功率谱法均与溶液的局域黏度以及球形颗粒的直径有关。当在样品池表面附近进行光阱刚度测量时[13]，黏度系数较为复杂，需要对黏度系数进行流体动力学修正，即需要考虑由壁效应额外增加的黏度[14]。而玻尔兹曼统计法无需考虑上述因素[12]。因此，当颗粒形状为非球形，或者在样品池表面附近进行光阱刚度测量时，玻尔兹曼统计法更适用。

本文描述了实验室搭建的近红外光镊系统，用玻尔兹曼统计法计算了样品池底面附近的光阱刚度，并分析和讨论了溶液温度的变化、四象限光电探测器的灵敏度、A/D转换器的采样频率以及采样时间对光阱刚度测量精度的影响。

2　测量原理和实验系统

2.1实验系统

单光阱近红外光镊实验装置示意图如图1所示。由光纤激光器发射出波长为1 064 nm的近红外激光经扩束后穿过棱镜，被二向色镜反射后进入浸油物镜(100×, NA=1.3, Nikon)，聚焦在充满介质的样品池中用于捕获样品池中的微球。被微球向后散射的光阱物镜收集，被二向色镜反射后穿过棱镜、透镜L1、滤光器后照射在四象限光电探测器上。样品池固定在xyz-压电平台上。CCD相机用于实时观测和记录。采集到的数据实时地传输到计算机，然后用Matlab软件进行数值计算和拟合。

实验中，采样数据的噪声主要来源于外界的振动干扰和光干扰。为了保证采样精度，这里主要采取了以下两种措施实现噪声隔离：在整个实验装置的组件中，光纤激光器的散热系统以及计算机的主机产生的噪声较大，除了这两种仪器之外，其它组件如四象限光电探测器、CCD相机等均搭置在气垫平台上，以隔离外界的振动干扰；将实验室做成暗室，采样过程在暗室中完成，以隔离外界的光干扰。

图1　单光阱近红外光镊实验装置Fig.1　Experimental setup of infrared optical tweezer with single optical trap

2.2测量原理

实验中，用四象限光电探测器获取被捕获微球的位移。四象限光电探测器(型号QP100-6，上海欧光科技公司)的驱动电路(自行搭建的)工作时输出的是模拟电压信号，经A/D采集卡(型号USB7660，16位AD转换，北京中泰研创公司)转化为数字信号由USB口输入计算机进行处理。在单光镊中，位移较小时输出电压U和微球位移x之间呈线性关系，有:

x=sU,

(1)

其中s表示四象限光电探测器的灵敏度。

在标定四象限光电探测器的灵敏度时，用xyz-压电平台驱动一个粘在样品池盖玻片上的微球穿过光阱中心，同时记录微球每移动一步后四象限光电探测器的输出电压。然后用直线拟合电压输出和微球位移之间的线性关系区域，拟合出的直线斜率倒数便是四象限光电探测器的灵敏度。具体操作时，令xyz-压电平台以0.1μm的步长沿x方向驱动粘在盖玻片上的2μm聚苯乙烯微球穿过光阱中心，得到四象限光电探测器的输出电压与微球位移(压电平台位移)之间的关系，如图2所示。拟合得到输出电压和微球位移之比为0.504 2μm/V。实验测量中，用记录的输出电压信号乘以灵敏度s，可得到被探测微球的位移。

光阱中被捕获微球的热驱动位移满足玻尔兹曼分布，微球的x向位移概率分布可以表示为[12]：

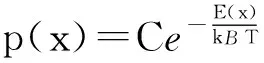
(2)

其中:E(x)为势能，kBT为热能(T是绝对温度，kB是玻尔兹曼常数)，C为概率分布的归一化常数。

图2　四象限光电探测器输出电压与微球位移之间的关系Fig.2　Relation between voltage output of quadrant photodiode and displacement of microsphere

由式(2)可得微球的势能分布，有：

E(x)=-kBTlnp(x)+kBTlnC,

(3)

其中：kBTlnC为势能偏移，为常数项，可以忽略。谐势阱的光阱中心附近区域具有谐势能分布。势能与位移以及光阱刚度的关系为：

(4)

利用式(4)拟合位移和由式(3)计算出的势能之间的关系，便可得到光阱刚度。

3　测量结果

实验中，激光器的功率设为0.43 W，2 μm的聚苯乙烯微球被捕获于距样品池底面3.5 μm处。A/D转换器的采样频率和采样时间分别为1 000 Hz和4 s。采集到的x向位移如图3(a)所示，位移的变化范围约为±65 nm。将位移分组间距设为1 nm，计算出位移的频率直方图分布，如图3(b)所示。将频率分布归一化成概率分布，然后根据式(2)计算势能分布，结果如图3(c)中的虚线所示。用谐势能分布拟合计算出的势能分布曲线如图3(c)中的实线所示，拟合得到的光阱刚度kx=7.05 pN/μm。

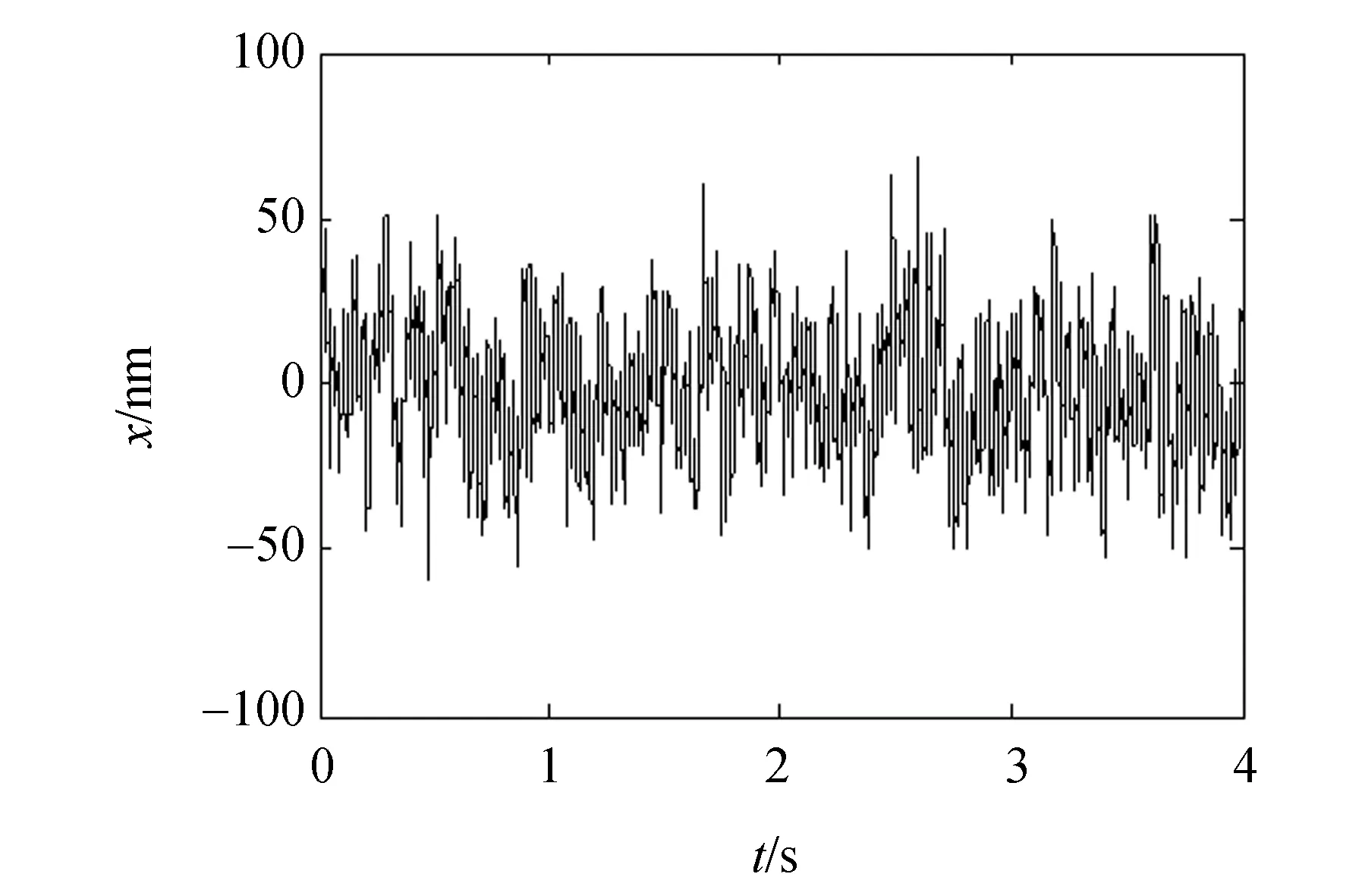
(a)x向的位移分布(a) x-displacement

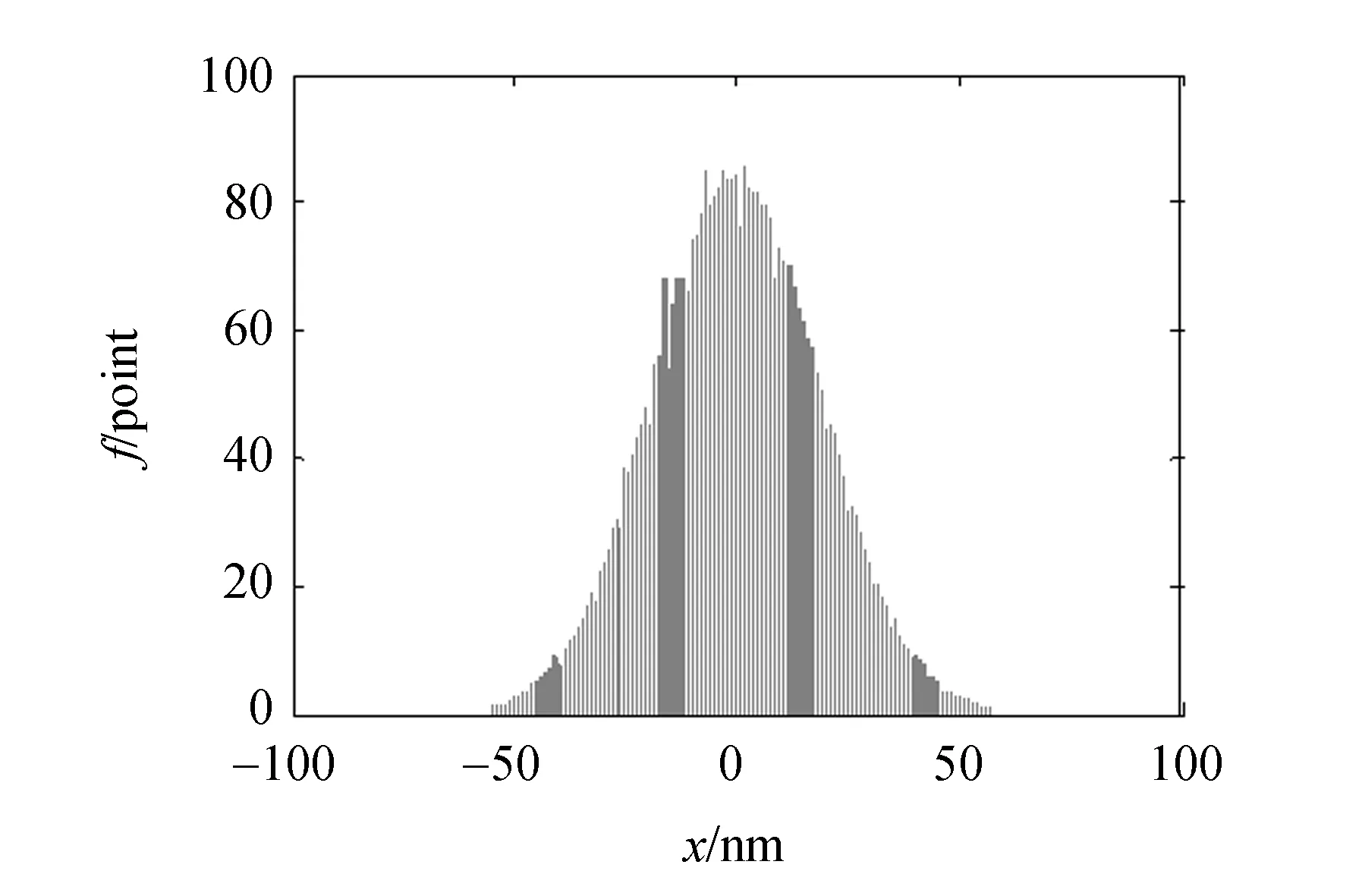
(b)频率分布 (b) Frequency distribution

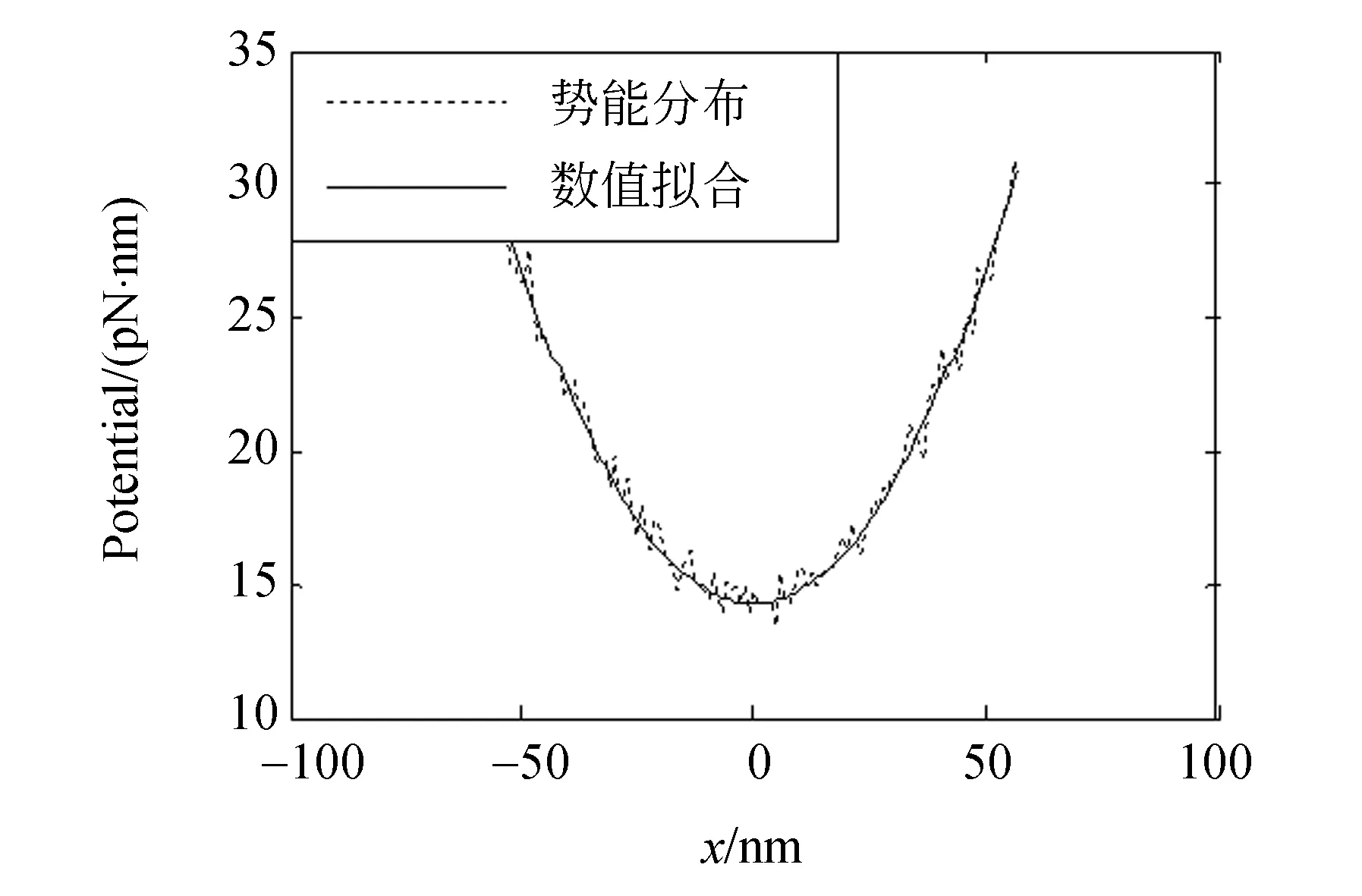
(c)势能分布以及数值拟合 (c) Potential distribution and its numerical fitting图3　利用玻尔兹曼统计法测量光阱刚度Fig.3　Measurement of optical trap stiffness using Boltzmann statistics method

4　分析和讨论

本文分析和讨论了溶液温度的变化、四象限光电探测器的灵敏度、A/D转换器的采样频率以及采样时间对光阱刚度测量精度的影响。

从式(2)和式(3)可以看出，利用玻尔兹曼统计法计算出的光阱刚度与溶液温度有关，有kx∝T。实验通常是在室温(25 ℃)下进行的，若温度变化1 ℃，光阱刚度计算值的相对误差为|kx1-kx2|/kx1∝|T1-T2|/T1=1/(273.15+25)≈0.34%。因此，用玻尔兹曼统计法计算光阱刚度时，温度变化对计算精度的影响很小。但用其它和溶液黏度有关的方法测量光阱刚度时，温度变化对光阱刚度精度的影响较大，如温度变化1 ℃，由水黏度变化造成的光阱刚度相对测量误差约为2.4%。

根据能量均分法，光阱刚度可以直接表达为[12]：

其中：〈x2〉表示被捕获微球的位置方差。对于四象限光电探测器的灵敏度s，有x∝s以及〈x2〉∝s2。由式(5)可知，kx∝1/〈x2〉，因而有kx∝1/s2，即光阱刚度反比于四象限光电探测器灵敏度s的平方。若灵敏度的相对误差为10%，光阱刚度测量值的变化以及相对误差如表1所示。可见，四象限光电探测器的灵敏度对光阱刚度的计算精度影响较大。因此，实验中需要多次标定四象限光电探测器的灵敏度并取平均，以获得高精度的灵敏度标定值，进而得到高精度的光阱刚度。实验中重复标定四象限光电探测器灵敏度5次，得到的重复测量精度为3.607 0×10-4μm/V。

表1　四象限光电探测器灵敏度对光阱刚度测量结果的影响

采集数据时需要选择合适的A/D转换器的采样频率。若采样频率过低，采集的数据不能完整地反映实际位移，使得计算出的光阱刚度存在误差。若采样频率过高，对相应电路的要求提高，数据量加大，分析处理数据的时间会增加。实际中，采样频率通常为被测频率的5～10倍，即可满足测量要求。这里被测频率是被捕获微球的拐角频率f0，即:

(6)

其中:β=6πrη，η是周围液体的黏度，r为微球半径。在实验中，采样频率为1 000 Hz，满足测量要求。

由于Allan方差[15]能够分辨系统中噪声或漂移占主导的时间段，为了获取采样时间对光阱刚度精度的影响，分析了被捕获微球位移的Allan方差与采样时间之间的关系。位移的Allan方差计算公式为：

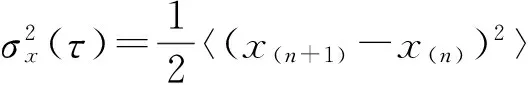
(7)

其中：x(n)是第n个采样周期内位移的平均值，τ为每个采样周期的时间。

实验中分别记录了100 s内(100,000个采样点数)固定微球、弱光阱(kx=7.05 pN/μm)以及强光阱(kx=23.35 pN/μm)捕获的微球位移，图4给出了相应位移的Allan方差分布。可以看出，这些曲线的趋势和Gibson等人[7]用高速相机测量2 μm硅球位移的Allan方差相似。与Gibson等人的最小Allan方差约0.6 nm相比，这里的方差约为0.4 nm，由此说明所采用的四象限光电探测器及其工作电路具有更小的测量噪声。对于捕获于弱、强光阱中的微球， Gibson等人的最小Allan方差分别约为1.5 nm和0.9 nm，而本文的分别约为3 nm和2 nm，均较高，这可能由压电平台的稳定性或其它因素造成的。另外，从图4可以看出，搭建的近红外光镊测量系统的最优采样时间在1～7 s。当采样时间小于1 s时，比如设为0.5 s，位移的频率直方图分布如图5(a)所示。可以看出，采样时间太短，测量系统中噪声所占的比例增加，使得采集到的热驱动位移不再符合规范的玻尔兹曼分布，因而不适于计算光阱刚度。当采样时间较长时，比如设为20 s，微球位移如图5(b)所示。可以看出，随着采样时间的延长，位移有整体上移的趋势，这是由系统漂移引起的。

图4　测量位移的Allan方差Fig.4　Allan variance of measured displacements

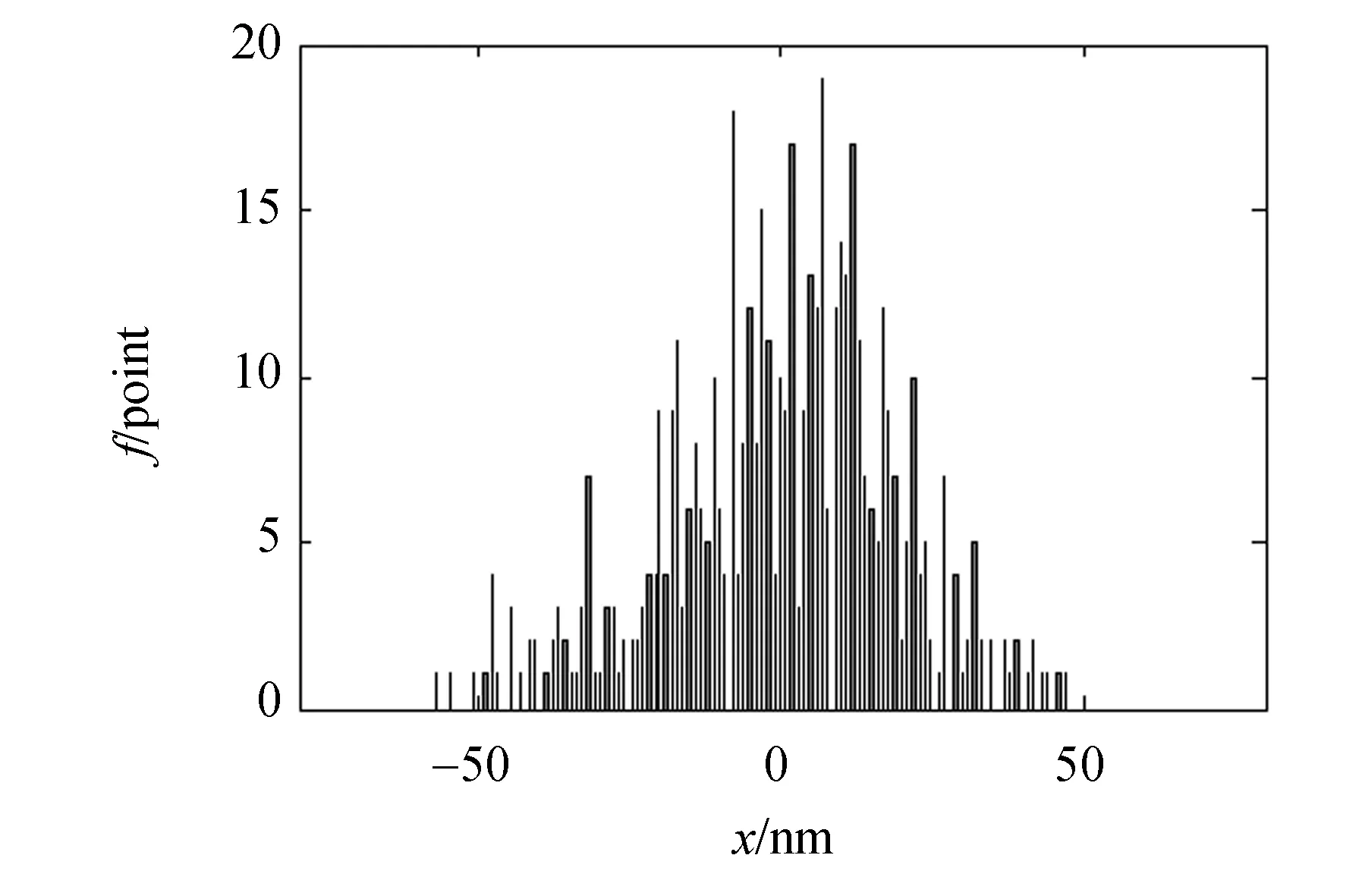
(a)位移频率分布(a)Displacement-frequency distribution

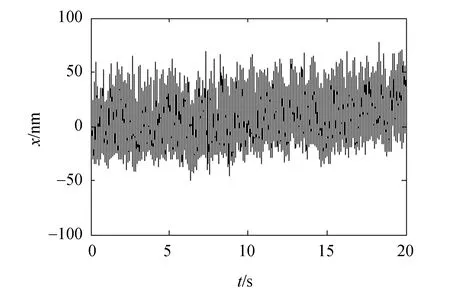
(b)位移随采样时间的变化(b)Variation of displacement with sampling time图5　采样时间分别设为(a)0.5 s时的位移频率直方图和(b)20 s时的位移Fig.5　(a) Frequency distribution as sampling time of 0.5 s and (b) displacement variation as range of sampling time of 20 s.

5　结　论

本文介绍了实验室搭建的近红外光镊系统，用四象限光电探测器探测被光镊捕获的微球向后散射的光，并采用玻尔兹曼统计法计算了样品池底面附近的光阱刚度。通过理论分析以及实验计算得出，相比于其它和溶液黏度有关的测量光阱刚度的方法，用玻尔兹曼统计法测量光阱刚度时，溶液温度的变化对光阱刚度的测量影响很小，可以忽略不计。测量出的光阱刚度值反比于四象限光电探测器灵敏度的平方，其精度受四象限光电探测器的灵敏度的精度影响较大，因此，实验中需要多次标定四象限光电探测器的灵敏度并取平均，以获得高精度的灵敏度标定值，进而得到高精度的测量光阱刚度。同时考虑到采样的完整性和数据处理的快速性，通常将采样频率取为被捕获颗粒拐角频率的5～10倍。此外，由Allan方差与采样时间的关系曲线可以看出，所搭建的近红外光镊测量系统最优的采样时间为1～7 s。本文的分析与结果对类似的测量实验具有指导作用。

[1]ASHKIN A, DZIEDZIC J M, BJORKHOLM J E,etal.. Observation of a single-beam gradient force optical trap for dielectric particles[J].OpticsLetters, 1986, 11(5): 288-290.

[2]翟晓敏，黄文浩. 光镊驱动微转子[J].光学 精密工程，2009，17(6)：1467-1472.

ZHAI X M, HUANG W H. Driving microrotor by using optical tweezers[J].Opt.PrecisionEng., 2009, 17(6)：1467-1472. (in Chinese)

[3]闫树斌，赵宇，杨德超，等. 基于近场光学理论光镊的研究进展[J]. 红外与激光工程，2015, 44(3): 1034-1041.

YAN SH B, ZHAO Y, YANG D CH,etal.. Optical tweezers based on near-field optical theory[J].InfraredandLaserEngineering, 2015, 44(3): 1034-1041. (in Chinese)

[4]PAUZAUSKIE P J, RADENOVIC A, TREPAGNIER E,etal.. Optical trapping and integration of semiconductor nanowire assemblies in water[J].NatureMaterials, 2006, 5(2): 97-101.

[5]HSU Y H, PRALLE A. Note: Three-dimensional linearization of optical trap position detection for precise high speed diffusion measurements[J].ReviewofScientificInstruments, 2014, 85(7): 076104.

[6]JACOBS M J, BLANK K. Joining forces: integrating the mechanical and optical single molecule toolkits[J].ChemicalScience, 2014, 5(5): 1680-1697.

[7]GIBSON G M, LEACH J, KEEN S,etal.. Measuring the accuracy of particle position and force in optical tweezers using high-speed video microscopy[J].OpticsExpress, 2008, 16(19): 14561-14570.

[8]RICE S E, PURCELL T J, SPUDICH J A. Building and using optical traps to study properties of molecular motors[J].MethodsinEnzymology, 2003, 361: 112-133.

[9]SIMMONS R M, FINER J T, CHU S,etal.. Quantitative measurements of force and displacement using an optical trap[J].BiophysicalJournal, 1996, 70(4): 1813-1822.

[10]VISSCHER K, BLOCK S M. Versatile optical traps with feedback control[J].MethodsinEnzymology, 1998, 298: 460-489.

[11]BERG-SØRENSEN K, FLYVBJERG H. Power spectrum analysis for optical tweezers[J].ReviewofScientificInstruments, 2004, 75(3): 594-612.

[12]FLORIN E L, PRALLE A, STELZER E H K,etal.. Photonic force microscope calibration by thermal noise analysis[J].AppliedPhysicsA:MaterialsScience&Processing, 1998, 66: S75-S78.

[13]DE MESSIERES M, CHANG J C, BRAWN-CINANI B,etal.. Single-molecule study of g-quadruplex disruption using dynamic force spectroscopy[J].PhysicalReviewLetters, 2012, 109(5): 058101.

[14]FAXEN H. The resistance against the movement of a rigour sphere in viscous fluids, which is embedded between two parallel layered barriers[J].AnnalenderPhysik, 1922, 68(10): 89-119.

[15]ALLAN D W. Statistics of atomic frequency standards[J].ProceedingsoftheIEEE, 1966, 54(2): 221-230.

朱春丽(1990-)，女，安徽宿州人，博士研究生，2011年于中国科学技术大学获得学士学位，主要从事光电测试技术方面的研究。E-mail: yatlili@mail.ustc.edu.cn

导师简介:

李静(1968-)，女，安徽合肥人，副教授，硕士生导师，1991年于同济大学获得学士学位，2005年于中国科学技术大学获得固体力学博士学位，主要从事光电技术和仪器方面的研究。Email: lijing@ustc.edu.cn

(版权所有未经许可不得转载)

Analysis of stiffness measurement precision of optical trap with Boltzmann statistics method

ZHU Chun-li, LI Jing*

(DepartmentofPrecisionMachineryandPrecisionInstrumentation,UniversityofScienceandTechnologyofChina,Hefei230027,China)

The stiffness measurement precision of an optical trap is a key in optical force measurement, so this paper proposes a method based on Boltzmann statistics to analyze the stiffness measurement precision of the optical trap. Firstly, a near infrared optical tweezer was introduced and it was built on an air cushion platform in a dark room to isolate light interference and vibration interference. Then, a quadrant photodiode was used to detect the backscatter light of a microsphere captured by the tweezer and the Boltzmann statistics method having no relation with solution viscosity was adopted to calculate the optical trap stiffness near the bottom surface of the sample cell. Finally, the influences of the solution temperature, the sensitivity of the quadrant photodiode, sampling frequency, and the sampling time on the accuracy of the optical trap stiffness measurement were analyzed and discussed. Theoretical analysis and practical calculation results indicate that the solution temperature has a little effect on the measurement, but the sensitivity of the quadrant photodiode influences on the measurement precision greatly. In consideration of complete sampling and higher data processing speeds, the sampling frequency is set 5 to 10 times as great as the knee frequency of the optically trapped microsphere. For the measurement setup proposed in this paper, the sampling time is set in the range 1-7 s, which ensures the higher measurement precision of the optical trap.

optical tweezer; near-infrared optical tweezer system; optical trap stiffness measurement; Boltzmann statistics method

2016-03-22；

2016-05-03.

国家973重点基础研究发展计划资助项目(No.2012CB937500);国家自然科学基金资助项目(No.91023049)

1004-924X(2016)08-1834-06

TN216

A

10.3788/OPE.20162408.1834