一种快速的基于稀疏表示和非下采样轮廓波变换的图像融合算法

赵春晖 郭蕴霆



一种快速的基于稀疏表示和非下采样轮廓波变换的图像融合算法

赵春晖*郭蕴霆

(哈尔滨工程大学信息与通信工程学院 哈尔滨 150001)

为了提高图像融合的效率和质量，该文提出一种基于快速非下采样轮廓波变换(NSCT)和4方向稀疏表示的图像融合算法。该方法首先对源图像进行快速NSCT分解，生成一系列低通和高通子带。对于低频子带，利用自适应生成的DCT过完备字典进行快速的4方向稀疏表示和系数融合；对于高频子带，则利用高斯加权区域能量最大的融合规则进行系数融合。快速NSCT将传统NSCT的树形滤波结构转变为多通道滤波结构，能成倍提高分解效率；快速的稀疏融合则抛弃了传统的滑动窗口方法，以水平、垂直、对角线4个方向进行稀疏表示和稀疏融合，进一步提高算法效率。实验结果表明，提出的快速算法能在不影响融合质量的条件下将算法效率提高近20倍。

图像处理；图像融合；非下采样轮廓波变换；稀疏表示；快速算法

1 引言

由于成像机理和技术限制，单一传感器获取的图像并不能反映被观测对象的所有特征，因此需要对不同传感器图像中的有用信息进行提取，并融合成一副具备更完整信息，并有助于人类观察和处理的图像。

目前，已经有大量的图像融合算法被相继提出，其中基于多尺度分析的图像融合算法从多尺度金字塔变换[1]开始，经由小波变换[2]，脊波变换[3]，曲波变换[4]等一系列算法发展，已取得了良好的融合效果。作为多尺度分析算法的代表，非下采样轮廓波变换(Non-Subsampled Contourlet Transform, NSCT)[5]于2006年被提出，它在轮廓波变换(Contourlet Transform, CT)[6]的基础上引入非下采样思想，保证了分解过程中的平移不变性，解决了传统算法在图像分解时的频谱混叠问题，获得了渐进最优的图像分析结果。在此基础上，学者们相继提出了不少行之有效的新算法，文献[7]将闭环反馈与NSCT相结合，获得较佳的鲁棒性和融合清晰度。文献[8]则将冗余提升小波变换与NSCT相结合，并引入新的多尺度分解算子与WA-WBA融合规则，能有效保持融合图像细节。然而，这些算法的计算复杂度较高，制约了它们的广泛应用。

近年来，随着稀疏信号表示理论的发展，稀疏表示(Sparse Representation, SR)作为一种有效的信号处理手段已被应用于图像融合领域中。与传统的基于像素值和像素邻域统计量的融合规则不同，稀疏表示提供了一种以原子结构特征为基本单元的融合手段，能够提取像素间更深层次的结构特征并加以融合，以提供更优的图像融合结果，因此得到图像融合领域的广泛关注。文献[9]将稀疏融合方法直接应用于灰度图像，并测试了不同的过完备字典对融合质量的影响。文献[10]将稀疏与多尺度分解相结合，克服了稀疏表示对高频信息不能完美逼近的缺点。文献[11]将剪切波变换(Shearlet Transform, ST)与稀疏表示相结合，并应用于医学图像处理，取得了良好结果。然而，在这些方法中都使用了滑动窗口模型，存在巨量的冗余计算。此外，这些方法通常使用复杂的字典训练模式，对不同类型的图像适用性差，也影响了算法的效率。

因此，为了解决上述问题，本文提出一种基于快速NSCT和4方向稀疏表示的融合方法FNSCT- FDSR(Fast NSCT-Four Direction Sparse Representation)，利用多通道滤波器结构代替NSCT中的树形滤波器结构，提高多尺度分解效率；利用4方向稀疏表示方法代替传统的滑动窗口稀疏表示方法，减少算法的冗余计算量，进一步提高融合算法的处理效率。

2 非下采样轮廓波变换

非下采样轮廓波变换(NSCT)是在CT的基础上，采用上采样滤波器代替以往分解过程中的下采样，避免了采样过程导致的频谱混叠，保证了分解过程中的平移不变性。它由非下采样金字塔(Non- Subsampled Pyramid, NSP)和非下采样方向滤波器组(Non-Subsampled Directional Filter Bank, NSDFB)两个部分组成。

NSP是通过非下采样塔式滤波器组，将源图像迭代分解为不同频带的等大小子图，保证NSCT的多尺度特性的过程。一个级NSP分解将生成一副低频子带图像和幅不同尺度的高频子带。图1(a)给出3级NSP的滤波器组结构和相应的频率切分图。

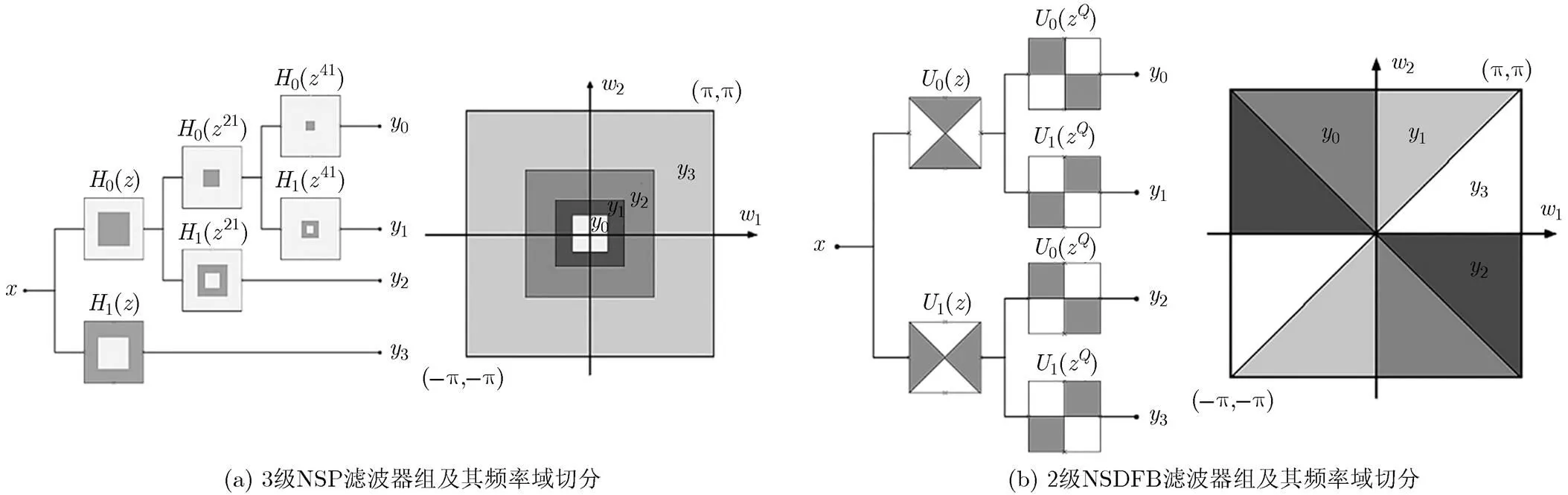
图1 滤波器组结构和相应的频率切分图

NSDFB是通过树形结构的方向滤波器组对NSP获取的各级子带图像进行方向分解，以提供图像的多方向信息。一般而言，每一级的NSDFB分解将会生成2幅方向子带，其中表示分解级别。图1(b)给出一个2级NSDFB的滤波器组结构和相应的频率切分图。

在NSCT中，每级滤波器都是由上一级的滤波器通过旋转和上采样得到，无需重新设计滤波器。分解所得的每一级子图都与源图像具有相同的大小，这与在分解过程中采用下采样操作的传统多尺度分解方法(如2维小波变换，轮廓波变换等)有着本质的不同。该性质确保了图像分解过程中的平移不变性，克服了频谱混叠现象，但同时也导致了相对较高的计算复杂度，影响了图像分解的效率。

3 信号的稀疏表示理论

3.1 稀疏表示

信号的过完备稀疏表示，是利用一个具备大量冗余原子的超完备字典对输入信号进行线性近似表示的过程。由于字典的过完备特性，用于线性近似表示信号的原子个数通常较少(即是稀疏的)，其中原子个数最少的表示(即最稀疏表示)为稀疏表示的理想解，其数学模型为

3.2 字典选取

在信号的稀疏表示中，过完备字典的选取直接影响到信号表示的有效性，包括稀疏度和误差值。目前行之有效的字典选取主要包括两种：一种是解析字典，通过预设的数学模型构建满足需求(原子维数和字典大小)的过完备字典，常用的包括DCT、小波变换字典等；另一种是学习字典，通过对大量样本数据进行训练，得到更有针对性的过完备字典，目前常用的字典训练算法主要有最优方向法(Method of Optimal Directions, MOD)和SVD[13]等。通常而言，解析字典是由数学模型直接获得，获取简单且具有较高的普适性，但对图像的高频细节匹配性差，直接表现为较高的误差值和稀疏度；而训练字典的误差项和稀疏度相对较小，但其适用范围与训练样本直接相关，普适性较差且训练成本高。

由分析可知，解析字典与训练字典的主要性能差异体现在对高频细节信息的逼近能力上。然而，由于在本文中采用了NSCT多尺度分析方法，稀疏融合只在低频子带中应用，无需对图像的高频细节信息进行逼近表示，因此，普适易用、获取成本低的解析字典显然具有更高的适用性，本文采用DCT过完备字典对图像进行稀疏表示。

4 基于快速NSCT和4方向稀疏表示的图像融合算法

4.1 多尺度分解：快速NSCT

由对NSCT的介绍中可知，NSCT被分解为NSP和NSDFB两个部分，每个部分各自包含一组多级滤波器结构。也就是说，要获取一副子带图像，需要对源图像进行多次滤波，这显著降低了图像分解的效率。因此，若对每个分解子带重新设计一个滤波器，将传统的树形结构滤波器组转变为多通道滤波器组，使每个子带图像的获取都只需经过一次滤波，则可以明显提高算法效率。图2给出2级快速NSCT与传统NSCT的滤波器结构对比。

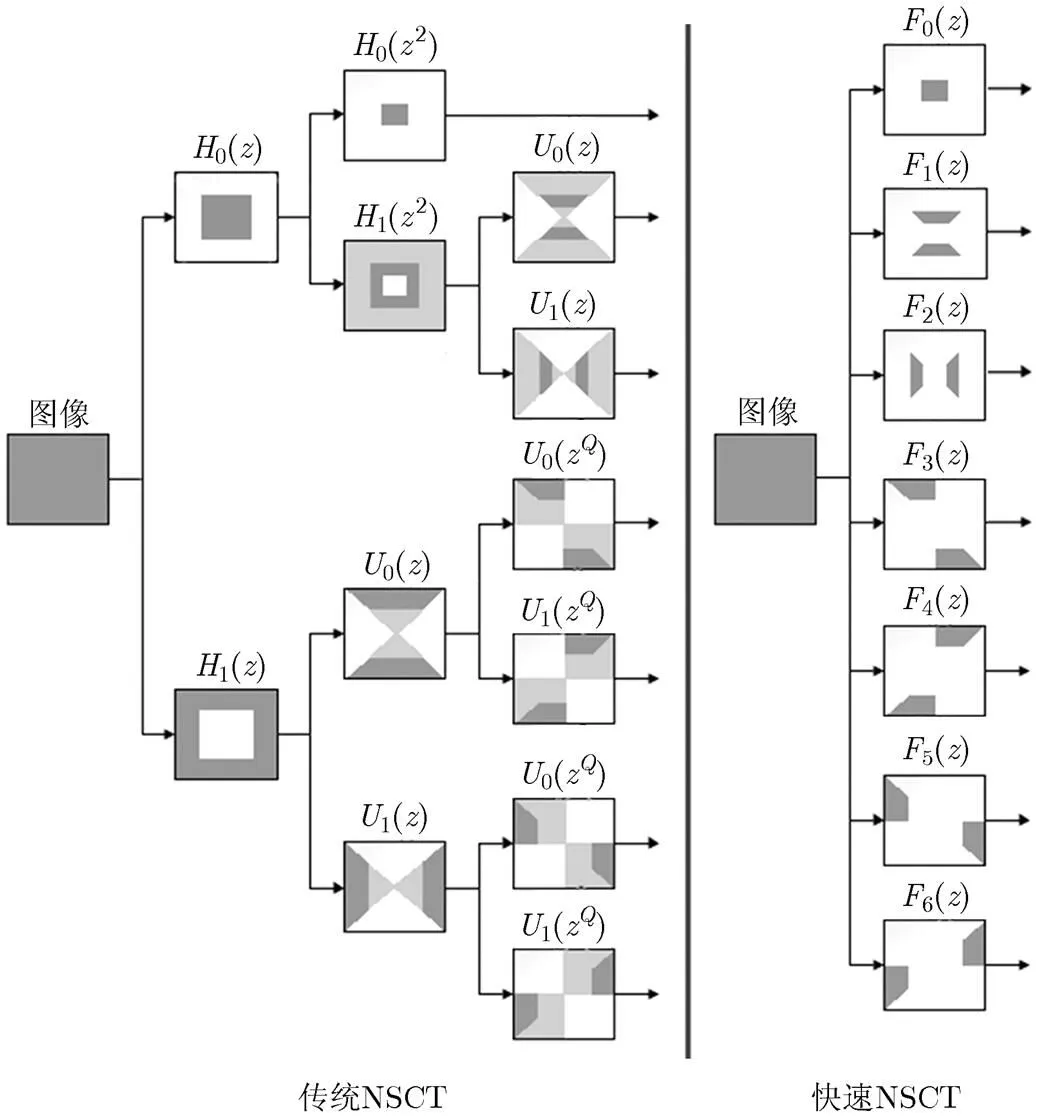
图2 2级快速NSCT与传统NSCT结构对比

如图2所示，在快速NSCT中，传统NSCT的树形滤波器组结构被多通道滤波器组所代替，假定NSCT滤波器结构为2叉树结构，在级分解中，滤波器个数可由传统NSCT的个，减少至快速NSCT的个，对图像进行滤波运算的次数相应减少，因此快速NSCT相比传统NSCT能提高相应倍率的分解效率。

由于2维滤波的过程的计算复杂度为(4)，同时滤波器的尺寸远小于图像大小，因此重新设计通道滤波器的时间相对图像滤波处理的时间可以忽略不计。

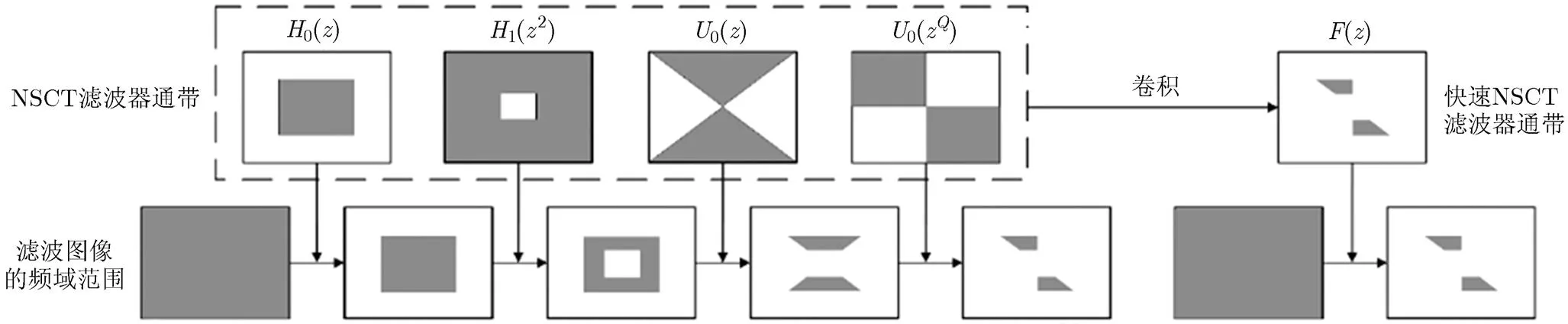
图3 快速NSCT通道滤波器实现

由图3和式(2)可知，快速NSCT滤波器是由传统的NSCT滤波器卷积合并得到，它与NSCT滤波器组具有相同的频域特性和滤波性能，满足传统NSCT滤波器组中的正交性和紧支撑性。需要注意的是，滤波器的卷积合并过程会造成滤波器的尺寸增加，需要对合并后的滤波器进行阈值为边缘截断(即将滤波器中小于的权值置0)。注意到图像的灰度级别为256级，图像存在值为1/512的固有量化误差，而滤波器的截断误差远小于该值，因此快速NSCT实现不会影响算法的分解和重构性能[14]。

下面给出快速NSCT的具体实现步骤：

(2)根据分解级别，通过梅花采样矩阵对滤波器进行旋转和上采样，获得相应的各级滤波器。

(3)将每一个通道的一组滤波器卷积合并，生成单一的通道滤波器，并去除值为零的滤波器边界。

(4)将源图像直接经过每个通道滤波器滤波，获得分解结果。

同样的方式适用于重构滤波器组设计，将各分子带图像经过相应的多通道重构滤波器滤波，并将滤波结果直接求和以获得重构图像。

4.2 低频融合规则：4方向稀疏表示

在稀疏表示中，由于稀疏性的要求，过完备字典的大小与原子维数成正相关，图像的数据量又相对较大，若直接对整幅图像进行稀疏表示，则需要极为庞大的过完备字典规模，这反过来又加剧了OMP等稀疏系数求解算法的复杂性。此外，图像的大小不一，不同图像间的字典无法通用。因此，直接对图像进行稀疏表示是不可行的。在现有的稀疏融合规则中，子带图像被划分为同样大小的块，采用滑动窗口的形式对每一个窗内的图像块进行稀疏表示和融合。这种折中方法统一了字典的原子维数，更易于稀疏系数的求解和融合。然而，滑动窗口虽然减少了字典的规模和稀疏求解算法的复杂度，但是引入了巨量的冗余计算：以常用的8×8窗大小为例，在窗滑动过程中，一个图像像素(除边缘外)会被64个不同的窗选定并作为信号的一部分参与稀疏求解，也就是说，一个像素信息在传统稀疏表示中需要被重复计算64次，严重影响图像的融合效率。

为了解决上述问题，本文提出一种4方向稀疏表示(Four-Direction Sparse Representation, FDSR)，抛弃传统的滑动窗口模型来提高融合效率。4方向包括水平、垂直、和4个方向，采用稀疏字典对每个方向上的一列(或一行)像素进行稀疏表示和系数融合，最后对获得4个方向上的融合图像进行平均，获得最终的融合结果。在该过程中，每个像素的信息只被计算它在4个方向信号上的贡献，相较传统稀疏表示算法，重复计算次数从64次减少到4次，大大提高了算法速率。此外，由于FDSR方法使用的是图像在4各方向上的行列信号，较传统稀疏表示的块状窗口能提供更多的方向信息，提高融合效果。

图4给出4方向稀疏表示模型的示意图，其具体步骤如下：

(1)对低频图像进行镜像边缘扩展，避免稀疏表示边界效应并方便字典原子维数设计。

(2)根据边缘扩展后的图像大小，生成两组DCT过完备字典1和2，其原子维数分别等于图像矩阵的行数和列数。

(3)参照图4，对源图像进行4方向稀疏表示，求解稀疏系数。

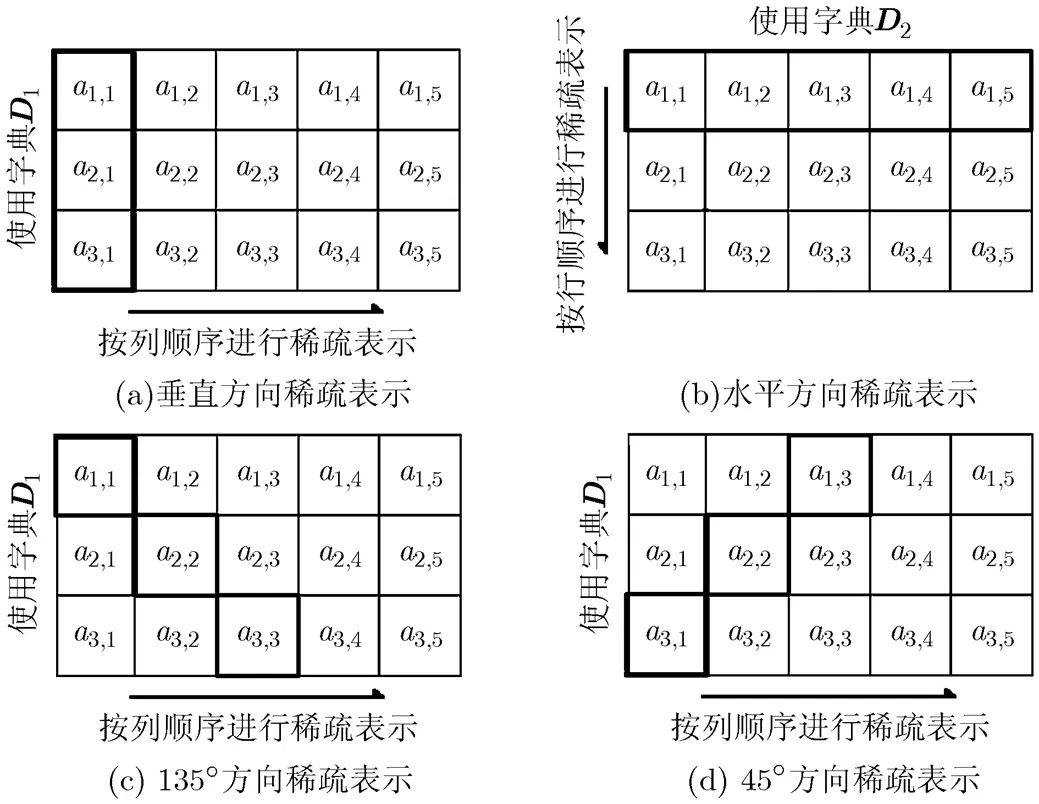
图4 4方向稀疏表示示意图

其中，为稀疏表示系数；=1,2,3,4，分别代表水平、垂直、和4个方向；为相应方向上的输入图像。

(4)分别对4个方向上的稀疏表示进行融合重构，采用取稀疏系数较大值的方式构建融合稀疏系数。

其中，上标,,分别表示低频源图像、低频源图像和低频融合图像。

(5)将4个方向上的融合图像取平均，获得最终的低频融合图像。

其中，表示最终的低频融合图像。

4.3 高频融合规则：高斯加权的区域能量估计

在快速NSCT分解所得的高频子带中，高频系数的值表示图像细节的变化情况，直接反映图像中的边缘信息和纹理细节分布。较大的高频系数值意味着更明显的边缘和纹理特征，需要在融合图像中被更好地保留。考虑到图像系数间的空间相关性，将对融合系数的权重求解建立在以系数为中心的小范围区域内的信息上是合理的。然而，由于中心系数与周边系数对权重估计的贡献不同，因此本文在区域能量估计(Regional Energy Estimate, REE)融合规则中引入高斯加权，对中心系数能量和周边系数能量分配不同的权值。高斯加权的区域能量估计(Gaussian Weighted Regional Energy Estimation, GWREE)融合规则如下：

(1)对每一个高频系数，根据式(1)计算其在3×3区域范围内的能量。

其中，s,j为高频子带第行第列系数的活度，为高频子带第行第列的系数值。高斯

(2)根据各系数活度值，计算融合系数：

其中，,分别为源高频系数子带，为融合高频系数子带。

4.4 算法整体框架

基于上述内容，将本文算法的整体结构在图5中给出。

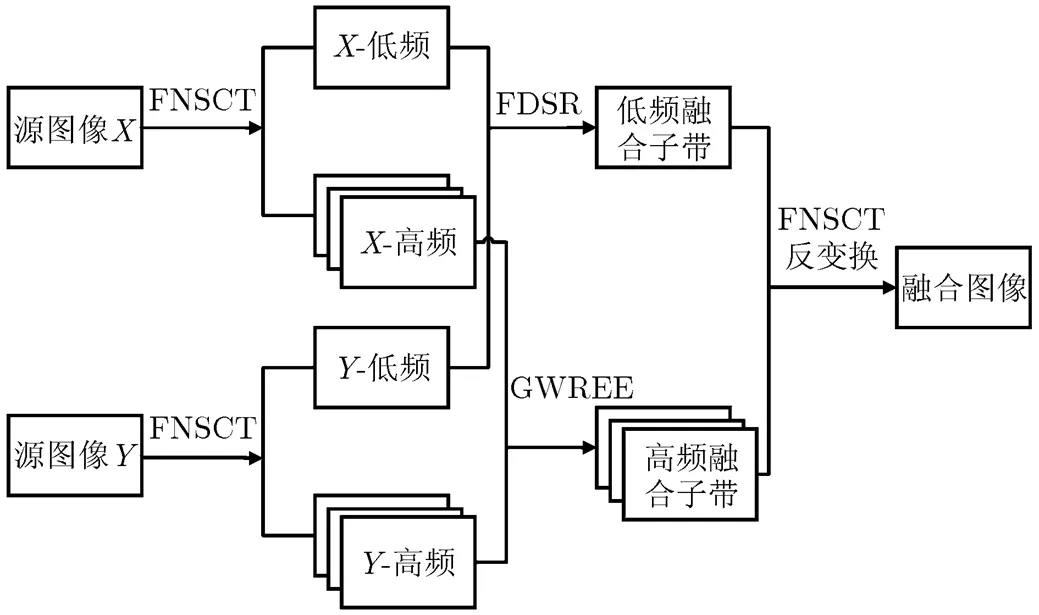
图5 算法流程框图

参照图5，详述本文算法具体步骤如下：

(1)根据4.1节设计快速NSCT多通道滤波器组，获取源图像的多尺度多方向分解子带。

(2)对低频子带，应用4方向稀疏表示融合规则，根据4.2节中步骤获取低频融合子带。

(3)对高频子带，采取高斯加权区域能量估计融合规则，根据4.3节中步骤计算融合系数，获取高频融合子带。

(4)将获得的低频融合子带和高频融合子带进行快速NSCT反变换，获得最终的融合图像。

5 仿真实验分析

将本文算法定义为FNSCT-FDSR，为了验证其的有效性，本文将它与基于SR[9]的图像融合方法、SR融合同步超分方法(SR-SR)[10]、采用K-SVD训练字典和小波变换的SR算法(WT-KSVD)[15]，以及基于SR与NSCT相结合(NSCT-SR)[16]的图像融合方法进行比较，其参数设置和融合规则选取按照相应文献中的描述设定。实验分别从主观评价指标、客观评价指标和耗时3个方面进行对比，实验数据包括“UN Camp”图像集(320×240)、“Garden”图像集(280×210)、“Clock”图像集(512×512)和“City”图像集(254×136)，如图6所示。实验环境为Intel Core i7-2630QM CPU 2.1 GHz, RAM 4 GB。

图6 实验用图像数据集

5.1 主观评价指标

主观评价指标是通过观察者对被观察图像进行评价，从图像的对比度、清晰度、可识别度等方面进行评价。主观评价指标具有简单、直观的特点，在图像融合评价中被广泛使用。

图7给出了4组图像集在不同融合方法下的融合结果，其中各列图像从左及右依次是，SR方法、SR-SR方法、WT-KSVD方法、NSCT-SR方法和FNSCT-FDSR方法的融合结果。由图7中的对比可知，本文算法在灰度范围和整体亮度上与源图像较为匹配，相较SR和NSCT-SR方法能保留图像更多的细节；SR-SR方法的层次感强，但细节丢失较严重；WT-KSVD方法则无法避免小波变换固有的方块效应和吉布斯现象。总而言之，除了在图像集“UN Camp”中对目标人物的突出不够明显外，本文算法相较前4者在主观评价指标上具有一定的优势。在“City”遥感图像集中，本文算法的色彩保真度和图像锐利度与NSCT-SR不相上下，高于SR算法和SR-SR算法，但在对比度方面略逊于WT- KSVD方法。

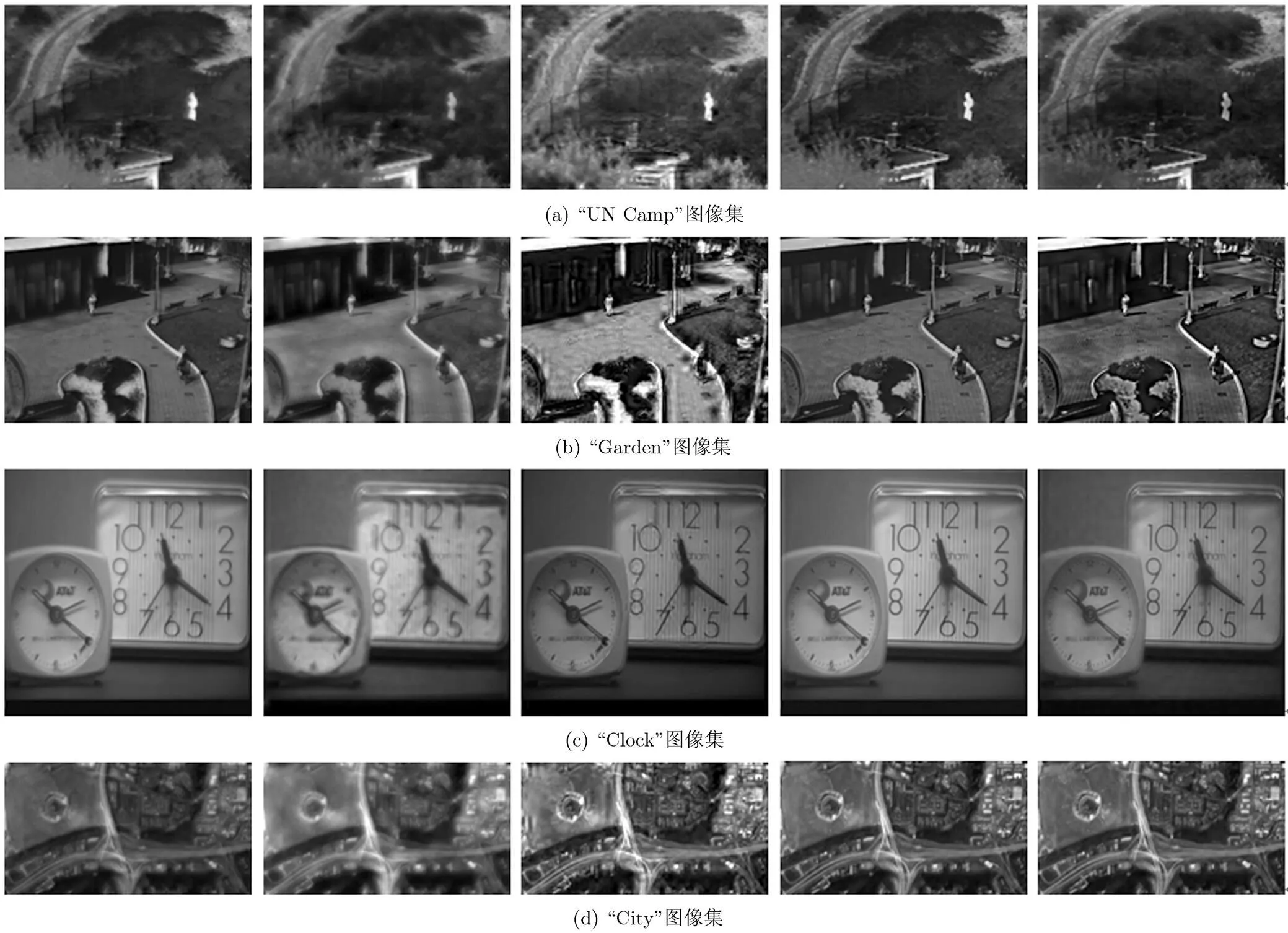
图7 图像融合结果对比

5.2 客观评价指标

主观评价指标虽然具有简明直观的特点，但受到观察者的主观意愿影响较大，并且对于相似度较大的融合图像的质量评估困难，因此，本文在主观质量评价指标之外引入互信息(Mutual Information, MI)、质量因子、视觉信息(Visual InFormation, VIF)和信息结构相似度(Structural SIMilarity, SSIM)4种客观评价指标对融合图像的质量进行定量评价[17]。MI反映融合图像从源图像中继承的信息量，因子从对比度、亮度和相关性3个方面综合评价融合质量，VIF主要评估图像受到的模糊、全局和局部对比度失真，SSIM则从图像的结构上评价图像与源图像的相似程度。除了互信息之外的评价指标的取值范围都在0~1之间，所有评价指标都是越大越好。评价结果在表1~表4中给出，最优指标由粗体标示。

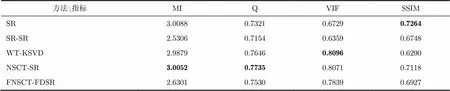
表1 “UN Camp”图像集融合质量评价指标对比

从表1~表4中可以看出，在“UN Camp”图像集中，本文算法在客观评价上稍逊，但影响不明显。而在另外4组图像集中，本文算法除了在互信息指标上有所不如，其余指标皆略优于其他算法。定量评价结果显示，本文算法在综合融合性能上与4种对比算法不相上下，甚至略有胜出。

5.3 时间分析

在图像融合中，除了图像融合的质量外，图像融合的时效性也是评价融合算法优劣的重要指标。然而，由于基于稀疏表示的图像融合算法采用了滑动窗口模型，相关文献大多回避了图像融合算法的耗时。本文对SR, SR-SR, WT-KSVD, NSCT-SR和FNSCT-FDSR 5种算法在4组不同大小的图像集上进行融合时间的对比，结果在表5中给出。

表5 各方法融合耗时对比(s)

从表5中可以看出，本文算法同时在图像分解和稀疏融合规则上采用了新的快速实现，相比传统的基于稀疏的图像融合算法而言，以十数倍计地提高了融合速度，结合前文中的融合质量分析，本文算法能在不影响融合质量的前提下，大幅提高图像融合的处理效率，证明了所提出算法的有效性。

6 结论

本文针对传统的NSCT与稀疏表示融合规则算法复杂度高、处理速度低的问题，提出一种基于快速NSCT和4方向稀疏表示的图像融合算法(FNSCT-FDSR)，在NSCT分解阶段采用重新设计多通道滤波器的方式提高分解和重构效率，在低频稀疏融合的阶段采用4方向稀疏表示方法替代传统的滑动窗口方式，进一步提高融合处理速度。实验结果表明，该方法在不影响图像融合质量，甚至还略有提高的前提下，能将图像融合的处理速度提高至原有的十数倍，是一种快速有效的图像融合算法。

[1] BURT P J and ANDELSON E H. The Laplacian pyramid as a compact image code[J]., 1983, 31(4): 532-540. doi: 10.1109/TCOM. 1983.1095851.

[2] LI H, MANJUNATH B, and ITRA S. Multisensor image fusion using the wavelet transform[J]., 1995, 57(3): 235-245.

[3] MINH N D and MARTIN V. The finite ridgelet transform for image representation[J]., 2003, 12(1): 16-28. doi: 10.1109/TIP.2002.806252.

[4] NENCINI F, GARZELLI A, BARONTI S,. Remote sensing image fusion using the curvelet transform[J]., 2007, 8(2): 143-156.

[5] CUNHA A L, ZHOU J, and DO M N. The nonsubsampled contourlet transform: theory, design, and applications[J]., 2006, 15(10): 3089-3101. doi: 10.1109/TIP.2006.877507.

[6] DO M N and VETTERLI M. The contourlet transform: an efficient directional multiresolution image representation[J]., 2005, 14(12): 2091-2106. doi: 10.1109/TIP.2005.859376.

[7] 杨晓慧, 贾建, 焦李成. 基于活性测度和闭环反馈的非下采样Contourlet域图像融合[J]. 电子与信息学报, 2010, 32(2): 422-426. doi: 10.3724/SP.J.1146.2008.01038.

YANG Xiaohui, JIA Jian, and JIAO Licheng. Image fusion algorithm in nonsubsampled contourlet domain based on activity measure and closed loop feedback[J].&, 2010, 32(2): 422-426. doi: 10.3724/SP.J.1146.2008.01038.

[8] 赵春晖, 马丽娟, 邵国锋. 采用WA-WBA与改进INSCT的图像融合算法[J]. 电子与信息学报, 2014, 36(2): 304-311. doi: 10.3724/SP.J.1146.2013.00542.

ZHAO Chunhui, MA Lijuan, and SHAO Guofeng. An image fusion algorithm based on WA-WBA and improved non- subsampled contourlet transform[J].&, 2014, 36(2): 304-311. doi: 10.3724/ SP.J.1146.2013.00542.

[9] YANG B and LI S. Pixel-level image fusion with simultaneous orthogonal matching pursuit[J].

, 2012, 13(1): 10-19.

[10] LIU Y, LIU S, and WANG Z. A general framework for image fusion based on multi-scale transform and sparse representation[J]., 2015, 24(1): 147-164.

[11] ZHENG Wei, SUN Xueqing, HAO Dongmei,. Thyroid image fusion based on shearlet transform and sparse representation[J].-, 2015, 42(1): 77-83.

[12] YAGHOOBI M, WU D, and DAVIES M E. Fast non-negative orthogonal matching pursuit[J]., 2015, 22(9): 1229-1233. doi: 10.1109/LSP.2015. 2393637.

[13] ZHENG Hao and TAO Dapeng. Discriminative dictionary learning via Fisher discrimination K-SVD algorithm[J]., 2015, 2015(162): 9-15.

[14] ZHAO Chunhui, GUO Yunting, and WANG Yulei. A fast fusion scheme for infrared and visible light images in NSCT domain[J].&, 2015, 2015(72): 266-275.

[15] 首照宇, 胡蓉, 欧阳宁, 等. 基于多尺度稀疏表示的图像融合方法[J]. 计算机工程与设计, 2015, 36(1): 232-235. doi: 10.16208/j.issn1000-7024.2015.01.042.

SHOU Zhaoyu, HU Rong, OUYANG Ning,Image fusion based on multi-scale sparse representation[J]., 2015, 36(1): 232-235. doi: 10.16208/j.issn1000-7024.2015.01.042.

[16] YIN H T, LI S T, and FANG L Y. Simultaneous image fusion and super-resolution using sparse representation[J]., 2013, 14(3): 229-240.

[17] QU G, ZHANG D, and YAN P. Information measure for performance of image fusion[J]., 2002, 38(7): 313-315.

Fast Image Fusion Algorithm Based on Sparse Representation and Non-subsampled Contourlet Transform

ZHAO Chunhui GUO Yunting

(,,150001,)

In order to improve the efficiency and quality of image fusion, a new image fusion algorithm based on four-direction Sparse Representation (SR) and fast Non-Subsampled Contourlet Transform (NSCT) is proposed. The proposed method firstly provides a series of low- and high-frequency sub-bands of source images via fast NSCT decomposition. Then adaptive DCT over-complete dictionary is used for the fast four-direction sparse representation and coefficients fusion of low-pass sub-band, while Gaussian weighted regional energy based fusion rule are used in high-pass sub-bands. Fast NSCT modifies the tree structure filter bank of traditional NSCT into multi-channel structure, and it saves about half of the time. The fast SR fusion method adopts a four-direction sparse representation for coefficients fusion instead of traditional sliding window method, and further improves the efficiency of algorithm. The experimental results show that the proposed fast fusion algorithm can improve the efficiency nearly 20 times without sacrificing fusion quality.

Image processing; Image fusion; Non-Subsampled Contourlet Transform (NSCT); Sparse Representation (SR); Fast algorithm

TP751.1

A

1009-5896(2016)07-1773-08

10.11999/JEIT150933

2015-08-13；改回日期：2016-04-07；网络出版：2016-05-24

赵春晖 zhaochunhui@hrbeu.edu.cn

国家自然科学基金(61571145, 61405041)，黑龙江省自然科学基金重点资助项目(ZD201216)，哈尔滨市优秀学科带头人资金(RC2013XK009003)

The National Natural Science Foundation of China (61571145, 61405041), The Key Program of Heilongjiang Province Natural Science Foundation (ZD201216), Excellent Academic Leaders Program of Harbin (RC2013XK009003)

赵春晖： 男，1965年生，教授，主要研究高光谱图像处理.

郭蕴霆： 男，1991年生，硕士生，研究方向为数字图像处理、图像融合.