基于熵权灰色关联分析的公共自行车服务评价*

陶超，李超，赵骞



基于熵权灰色关联分析的公共自行车服务评价*

陶超1，李超1，赵骞2

（安徽财经大学 1. 统计与应用数学学院，2. 财政与公共管理学院，安徽 蚌埠 233030）

研究了公共自行车服务系统站点的评价问题．运用SPSS软件对公共自行车站点的借车频次，还车频次等基本数据进行统计．选取站点累计借还车频次和可借车比等指标，在灰色关联分析理论的基础上提出一种利用熵值法求解权重的加权灰色关联评价方法，并对若干站点设置的合理性进行评分排序．得出结论并给出相应建议．

公共自行车；SPSS；熵值法；灰色关联

城市交通拥挤，空气质量下降，环境污染严重等一系列问题使人们开始转向绿色低碳生活．公共自行车作为一种低碳无污染的绿色交通工具深受居民的喜爱，公共自行车不仅有效地缓解了交通拥堵，解决了公交出行“最后一公里”的难题，更提高了城市的绿色竞争力，还有助于锻炼身体，减少的疾病的发生．但我国目前公共自行车服务站点仍有许多问题亟待解决[1]，如站点位置设置不合理，站点之间的调度不及时，索桩数量配置不合理等．因此，优化配置公共自行车服务系统对提高城市运行效率，增加居民满意度具有重要意义．

1数据清洗

本文的数据来源于温州市公共自行车服务系统181个站点20 d的借还自行车原始数据．在求解各个问题时，首先对原始数据进行筛选，并剔除以下异常数据：

（1）筛选出借还车数据表中借还车站均为同一站点，且借还车桩号相同的用车时间为0的数据；

（2）筛选出某4 d中站点号位1 000的站点数据，根据温州市鹿城区公共自行车管理中心网站提供的信息，站点号为1 000的站点为调试点，属于特殊情况；

（3）根据温州市鹿城区公共自行车管理中心网站提供的公共自行车服务指南上的租车流程（见图1），可以推断借还车站点相同且用车时间在1~2 min钟内的数据不符合实际情况，予以剔除；

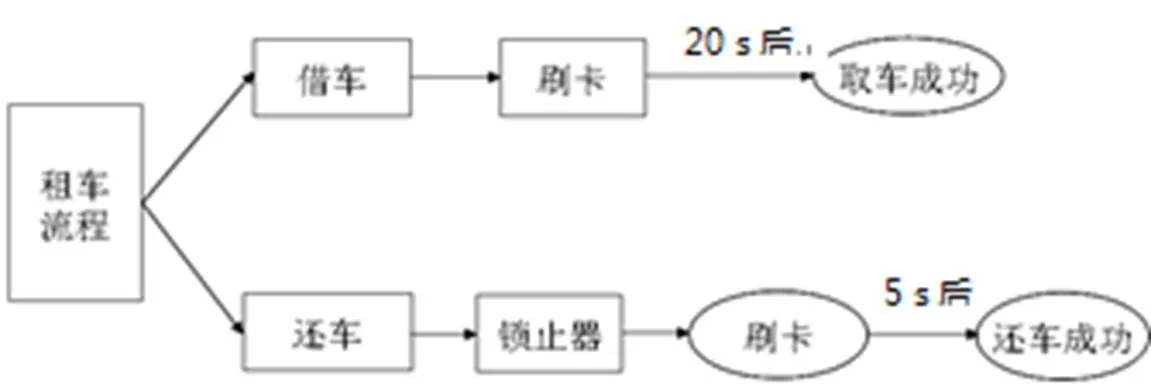
图1　温州市公共自行车借还车流程

（4）筛选出每天借换车数据中，借还车站点相同且用车时间在3~5 min的数据．根据温州市鹿城区公共自行车服务指南说明，借车时听到语音提示“通讯故障暂停使用，请等待3~5 min后，换桩借车”，因此予以剔除．

2站点累计借车、还车频次

2.1站点累计借车频次

运用SPSS软件统计181个公共自行车站点累计20 d的借车频次数据，得到累计借车频次分布图（见图2）和各站点排名情况（由于篇幅原因，本文只选取排名前10的站点），同时计算每个站点的累计借车频率（见表1）．

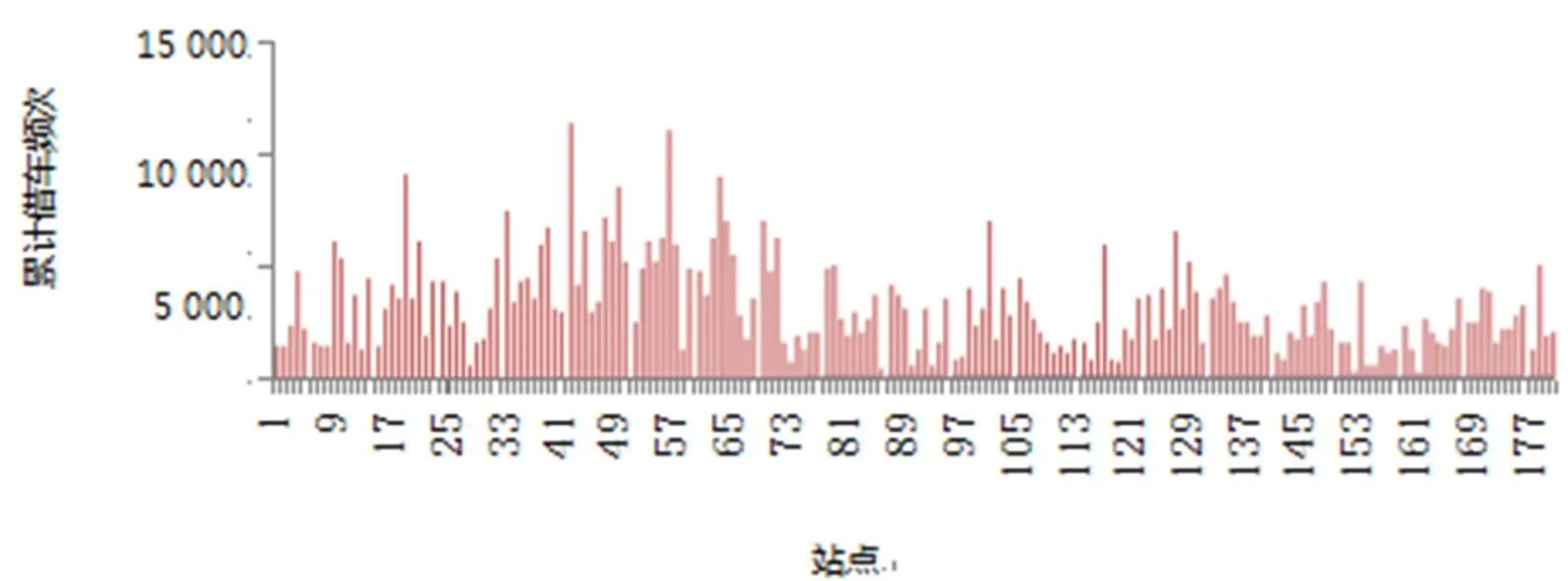
图2　各站点累计借车频次分布

表1　各站点累计借车频次排名

从图2和表1可以得出，公共自行车站点的累计借车频次分布差异较大，街心公园和五马林美食公园的累计借车频次最高，均达到了1万次以上，这与站点的地理位置和附近的人流量密切相关．

2.2站点累计还车频次

运用SPSS软件统计181个公共自行车站点累计20 d的还车频次，得到累计还车频次分布图（见图3）和各站点排名情况（由于篇幅原因，本文只选取排名前10的站点），同时计算每个站点的还车频率[2]（见表2）．

图3 各站点累计还车频次分布

表2 各站点累计还车频次排名

由图3和表2可以看出，公共自行车站点还车累计频次分布与借车累计频次的分布特征相似．五马美食林和街心公园的还车累计频次最高，同样也达到了1万次以上．从温州市地图可以发现，这2个站点处于交通发达地区，附近娱乐场所和办公区域较多．因此，温州市应适当在这些站点增加公共自行车数量和索桩数量以满足居民的需求．

3灰色关联模型的建立

3.1公共自行车服务站点评价指标的确定

基于借还车原始数据，从各站点的累计还车频数、累计借车频数、可借车比例、可还车比例及高峰时段的借换车差值等5个指标探究公共自行车服务系统站点设置的合理性[3]．其中，各站点的累计还车频率、累计借车频率反映了公共自行车服务站点的利用效率．可借车比例=可借车辆数/总车位数，可还车比例=剩余车位数/总车位数，反映了公共自行车站点服务的运行效率．高峰时段的借还车差值=|借车次数-还车次数|，反映了索桩数量配置的合理性．

3.2加权灰色关联模型的建立

灰色关联度的应用涉及社会科学和自然科学的各个领域，尤其在社会经济领域，如国民经济各部门投资收益、区域经济优势分析、产业结构调整等方面，都取得较好的应用效果．

灰色关联评价的前提是确定备选方案的参考序列（一般是最优方案的指标值）和比较序列，接着计算参考序列与比较序列的关联度大小，判断参考序列与比较序列发展过程的相似程度，进而以关联度为标准给不同备选方案评定等级[4]．

将公共自行车服务系统的站点设置视为有限个方案的多目标决策问题．共设有个站点，每个站点有个评价指标，以备选方案为行向量，评价指标为列向量，则可以得到每个站点和评价指标的原始评价值矩阵．设矩阵为中个指标的最理想参考评价数列（对效益指标取最大值，对成本指标取最小值），（），即，则与的灰色关联系数，式中：为分辨系数，且，的取值和问题的背景有关，通常取．

3.3熵值法确定指标权重

熵值法确定权重是基于样本数据自身的信息特征做出判断，可以有效地反映出指标信息熵值的效用值．在信息论中，信息与熵符号相反，但绝对值相等，信息是表示系统有序程度的一种度量标准，而熵则反映了系统的无序程度．根据这些性质，本文利用各公共自行车站点的评价指标基本信息，通过熵值法得到各个指标的信息熵，其中信息熵值越小，则表明该指标信息的无序程度就越低，信息的效用值就越大，指标赋予的权重就会越大[5]．

（6）计算加权关联度．现有的灰色关联度中没有考虑到参考数列和比较数列之间不同指标权重的大小，且最终每个方案的灰色关联只是算术平均值的结果[6]．因此，得出的结论可能存在不合理的地方．故利用熵值法确定权重后得到加权关联度．

4结果分析

从最终的评价结果可知，5个公共自行车服务站点设置合理程度的排名为：4号>1号>5号>3号>2号．

5结论及建议

（1）不同公共自行车借还车站点的借车频率和还车频率之间存在较大差异．因此，在频次高的站点应适当增加索桩数量以满足居民的需求[8]．

（2）公共自行车站点的利用效率与站点所处的地理位置密切相关，通常人流量较大的区域公共自行车的利用效率就越高．因此，在人群比较集中的繁华地带应增加站点数量，提高各站点之间的调配效率．

（3）从指标的权重向量可以看出，公共自行车服务站点的利用效率和高峰时段的服务效率在评价体系的指标权重中占比较大，在评价指标体系中起显著作用．因此，公共自行车服务系统应做好高峰时段应急的准备，以防止无车可借和无车位可还的现象发生．

[1] 杨杰．城市公共自行车租赁系统在中国的发展[J]．山西财经大学学报，2015，37（81）：63 -64

[2] 杨桂元，朱家明．数学建模[M]．上海：上海财经大学出版社，2015

[3] 刘引涛，刘楠．公共自行车服务系统站点及锁桩设置评价模型的分析研究[J]．电子设计工程，2014，22（23）：11-13

[4] 周会军，肖英杰，张浩，等．基于改进灰色关联分析法的码头设计方案优选[J]．上海海事大学学报，2011，32（3）： 11-15

[5] 李国良，付强，孙勇，等．基于熵权的灰色关联分析模型及其应用[J]．水资源与水工程学报，2006，17（6）：16-18

[6] 祝翔．公共自行车系统服务水平综合评价研究[D]．北京：北京交通大学，2011

[7] 庄轲．基于灰关联的公共自行车租赁点选址研究[J]．交通运输研究，2015（5）：31-36

[8] 谢小伟．对鹿城区公共自行车服务系统的评价和建议[J]．金华职业技术学院学报，2014，14（6）：57-59

Grey correlation analysis based on entropy weight of public bicycle service evaluation

TAO Chao1，LI Chao1，ZHAO Qian2

（1.School of Statistics and Applied Mathematics，2. School of Finance and Public Management，Anhui University of Finance and Economics，Bengbu 233030，China）

Researched the evaluation of the sites of public bicycle service system comprehensively．Firstly，with SPSS software，the frequency of borrowing bicycles and returning bicycles was derived from data．Then，with indicators like frequency of cumulative borrowing or returning bicycles and ratio of accessible bicycles，based on existing grey relational analysis theory，put forward an evaluation weighted grey correlation model whose weight is obtained by entropy method．And scoring and ranking rationality of several sites settings was performed．At last，gave conclusions and relevant recommendations．

public bicycle；SPSS software；entropy method；grey correlation analysis

1007-9831（2016）07-0017-05

O29∶U491.2

A

10.3969/j.issn.1007-9831.2016.07.005

2016-04-10

安徽财经大学大学生科研创新基金项目（XSKY1657）

陶超（1995-），男，安徽芜湖人，在读本科生．E-mail：18895612891@163.com

李超（1980-），男，安徽合肥人，副教授，博士，从事宏观经济统计分析研究．E-mail：lichao@aufe.edu.cn