多模态范畴语法和汉语部分“的”字研究

张　璐



多模态范畴语法和汉语部分“的”字研究

张璐

范畴语法是对自然语言信息进行可计算处理的逻辑语义体系。从20世纪70年代的蒙太古语法开始基于句法范畴和语义类型的对应来尝试处理英语部分语段，到目前多模态范畴语法对组合范畴语法和范畴类型逻辑的结合，都是为了能够取范畴语法体系中具有不同结构性质的类型逻辑系统的长处，以便更好地处理自然语言的句法和语义。汉语中独有的虚化成分“的”的可计算研究正体现了范畴语法的发展思路。

多模态范畴语法；混合范畴类型逻辑；汉语虚化成分“的”

20世纪70年代以来，随着蒙太古“普遍语法”思想的提出，逻辑与语言的交叉研究不断获得深入，从句法到语义都得到长足发展。作为这一交叉研究的基础，范畴语法的重要地位不得不提及。蒙太古对范畴语法与类型语义的探究是采取逻辑手段对自然语言的句法和语义进行形式化研究的起点，蒙太古的“部分语句系统”通过对范畴语法和类型逻辑的结合，实现了对自然语言句法和语义的对应推演。其后的逻辑学家对这一领域进行了不断深入的发掘，作为组合范畴语法和范畴类型逻辑结合的产物——多模态范畴语法正是这一研究的新兴分支。

“的”则是现代汉语中使用频率最高的虚词，其句法和语义表现都较为复杂，许多学者都曾从不同的角度对“的”进行过考察。黎锦熙可说是开现代汉语“的”字研究的先河，他区分

了4类不同的“的”，分别为：用于将名词或者名代词与另外的名词或名代词进行组合的特别介词，如“太阳的光”；用于形容词或具有形容词功能的词后的语尾词，如“可爱的少女”；用于替代实体词的连接代名词，如“做保洁的”；以及位于句末，用于加强肯定语态的语态助词，如“你几时返家的”*徐阳春：《关于虚词“的”及其相关问题研究》，上海：复旦大学，2003年。。吕叔湘认为“的”可以确认语气以及起到联结作用*吕叔湘：《中国文法要略》，北京：商务印书馆，1942年。。王力将“的”处理为两类，一类用作修饰语标记，另一类用作语气标记*王力：《中国现代语法》，北京：商务印书馆，1982年。。朱德熙将“的”作为词语后附成分分为三类，他认为“的”的句法语义功能是随着其所附着词语的不同而不同*朱德熙：《说“的”》，《现代汉语语法研究》，北京：商务印书馆，1980年，第67～103页。。“的”在现代汉语的口语及书面语中的出现频率都十分之高，对其句法功能的发展变化的研究具有重要的意义。据统计，目前依托宾州汉语树库转换的汉语组合范畴语法树库，按照现有组合范畴语法的分

析方法，“的”可以有多达181种范畴的指派，当之无愧成为范畴指派的第一名*参见陈鹏《汉语CCGBank构建》，2016年5月13日国家社科基金重大项目《自然语言信息处理的逻辑语义学研究》结项会报告。。对“的”字结构的深入研究无疑能够更好地服务计算机人工智能处理汉语自然语言信息。本文采用多模态范畴语法的手段，选取汉语中能够作为形容词附加成分使用的一类“的”字成分，试图保证带有“的”字的表达式能够获得与不带“的”字的表达式相同的语义分析。

一、多模态范畴语法的发展

采用形式化的办法进行自然语言句法和语义的并行处理始于蒙太古1969年发表的《作为形式语言的英语》(EnglishasaFormalLanguage)。其中，蒙太古认为计算机人工语言与自然语言并无本质差异的“通用语法”思想，启发了在他之后的逻辑学家和形式语义学家将组合原则应用到自然语言研究的方方面面，采取运算和推演的方式对自然语言的句法和语义进行形式化的处理*张璐、赵曼：《逻辑语义学中的组合原则》，《重庆理工大学学报》(社会科学版)2014年第9期。。范畴语法借助符号和推演来刻画自然语言，揭示自然语言的递归性，这正是当今时代计算机信息处理的要求。不同语种的语言之间有许多的共性，但也常常在细微之处存在差异，一个成熟的范畴语法理论应该能够在把握语言共性的同时，准确刻画不同语言的差异。这一要求启发了众多学者开始对范畴语法进行多模态扩展的尝试，比较具有代表性的有斯蒂德曼(M. Steedman)、贝德里奇(J. Baldridge)、黑普(M. Hepple)、莫哈特(M. Moortgat)、莫利尔(G. Morrill)等人。

多模态范畴语法是以传统范畴语法为基础发展起来的版本，其主要特点是通过将传统范畴语法发展的两个方向——基于词库的组合范畴语法和基于规则的范畴类型逻辑结合起来，一方面保证了自然语言句法语义推演的精确性，另一方面贯彻了彻底的词汇主义。通过在范畴类型逻辑系统中模拟组合范畴语法的多模态思想，为范畴语法的积算子和斜线算子添加模态下标，从而将范畴语法扩展为前提敏感的逻辑系统，这种处理方式有助于以少量的规则来把握自然语言处理的灵活多样性。据此构造出的系统是混合的范畴类型逻辑系统，我们称其为多模态范畴语法。邹崇理认为，对范畴语法进行逻辑系统的抽象，构造可能世界的框架语义解释，可以获得多模态范畴语法。范畴语法是多模态范畴语法产生的基础*邹崇理：《多模态范畴逻辑研究》，《哲学研究》2006年第9期。。

多模态范畴语法兼具组合范畴语法与范畴类型逻辑的特征。首先，作为主体内容的组合范畴语法体系是英国计算语言学家斯蒂德曼创立的。而在利用组合范畴语法对自然语言表达式进行研究的过程中，贝德里奇观察到，对于语序灵活的语言来说，组合范畴语法的处理方式不够理想。有些语言比如汉语，需要灵活的组合规则刻画自然语言表达式中成分组合方式的多样性；但是对于像英语这样具有较强语法特征的语言，灵活的组合规则则是不必要的，如果在语法体系中添加这类规则，反而会造成不合语法的过度生成*Jason Baldridge, Lexically Specified Derivational Control in Combinatory Categorial Grammar, Satland: University of Edinburgh, 2002.。因此，贝德里奇通过对斜线算子增加模态下标这一方式，限制了语法规则的使用范围及其过度的生成力，实现了对组合范畴语法的多模态扩充。作为范畴语法的分支，多模态组合范畴语法与范畴类型逻辑在规则上并没有太大的差异，区别仅在于二者关注的重点不同。多模态组合范畴语法关注的是语言学的应用，而范畴类型逻辑关注的则是逻辑系统自身所具备的种种性质。因此，多模态范畴语法的主体内容就是多模态组合范畴语法。

其次，范畴类型逻辑是一种形式化的工具，以函项运算和逻辑推演的手段，对语言(包括形式语言和自然语言)进行分析。函项运算是取自代数的概念，推演则是逻辑的根本，所以，就范畴语法中的这一分支来说，在体现出数学、逻辑学、语言学的跨学科特征的同时，尤为强调对规则的刻画，是一套基于规则的语言描写体系。范畴类型逻辑的研究目的是为自然语言的句法和语义提供一套演绎的刻画系统，莫哈特将其中心思想描述为“形式语法即逻辑”(formal grammar is presented as a logic)*M. Moortgat, Categorial Type Logic, eds by J. van Benthem and A. ter Meulen, Handbook of Logic and Language, Amesterdam: Elsevier Science B. V., 1997, p. 96.。在多模态组合范畴语法研究的基础上，我们可以向范畴类型逻辑的系统中引入模态算子，将范畴类型逻辑扩展为前提敏感的混合逻辑体系，获得受限的结合公设与交换公设，同时无需对通用的范畴语法规则进行增删，由此获得的多模态范畴语法能够进行不同语种间语言现象的灵活处理，有利于我们从深层角度把握自然语言的特征和规律。因此，多模态范畴语法就是多模态组合范畴语法与范畴类型逻辑结合的产物。

二、多模态范畴语法的构成

我们知道，范畴类型逻辑系统中包含四种不同的兰贝克演算。贝德里奇在组合范畴语法系统内尝试以★、◇、× 以及◎作为斜线算子的基本模态下标，令带有各种不同下标的斜线算子适用于不同的函子范畴的推演规则。斜线算子的结合和交换对应范畴类型逻辑中的系统分别为：带下标★的斜线算子是最受限的，仅适用于范畴语法中最基本的函项应用规则，相当于NL系统(非结合非交换的兰贝克演算)；带下标◇的斜线算子适用于组合函子B和置换算子S的函项应用规则，相当于L系统(兰贝克演算)；带下标×的斜线算子允许推演中规则跨越表达式的相邻成分，相当于NLP系统(交换的兰贝克演算)；带下标◎的斜线算子适用于所有的范畴推演规则，即对应于LP系统(既结合又交换的兰贝克演算)。也就是说，贝德里奇实际上是通过为斜线算子添加模态下标，将四种类型的兰贝克演算置于统一的系统当中。

在组合范畴语法恪守词汇主义的做法中，对函子范畴的斜线算子添加模态标记就能够获得不同的语法体系。那么在范畴类型逻辑恪守规则主义的做法中，我们可以通过增删结构公设，对组合范畴语法进行多模态的模拟范畴，获得具有不同推演能力的逻辑层级，这种做法实际上是对子结构逻辑的发展。

传统范畴类型逻辑的公理系统可以进行如下表述：

Ⅰ.句法部分

F∷ =A|F/F|FF|F·F|

公理和结构公设：

I：A→A等同公理

通常的冗余规则和传递规则：

(1)A→C/B├ ┤A·B→C├ ┤B→AC

(2)A→B,B→C├ A→C

Ⅱ.语义解释

系统的框架语义学为三元框架< W, R3>：

原子公式的语义赋值为：v(p) ⊆ W

(1)v(A·B) = {x | ∃y∃z[Rxyz & yv(A) &zv(B)]}

莫哈特认为多模态范畴语法系统作为组合范畴语法与范畴类型逻辑结合的产物，不是将两种系统的优势简单结合，作为一个混合的逻辑体系，它有自己的特点——模态算子之间的关联(linkage)，其相应的结构规则如下*M. Moortgat, R. Oehrle, Logical Parameters and Linguistic Variation. Lecture Notes on Categorial Grammar, Fifth European Summar School in Logic, Language and Information, Lisbon, 1993.：

关联规则

A ·jB→A ·iB

关联规则体现了混合的逻辑系统之中，不同层级的子结构相互之间的关系。借由这一规则，兰贝克演算的模态算子之间能够相互转换，增加了推演前提的敏感性，在不增加逻辑系统复杂程度的基础上，获得了对逻辑系统的扩展，使得系统具备了更加充分且精确的生成能力、刻画能力以及解释能力。不难看出，在范畴类型逻辑中斜线算子的模态下标j可以指多模态组合范畴语法的模态标记★，而i则可以指模态标记◇。由此，对传统的范畴类型逻辑通过增删结构公设，就能够获得范畴类型逻辑的不同系统，这些系统构成子结构逻辑的层级，经由关联规则，我们可以实现不同子结构逻辑层级之间的沟通过渡，获得更加适合处理自然语言的多模态范畴语法体系。

毗连算子相关的结构公设有两条：

仅保留传统范畴类型逻辑公理系统中的等同公理、冗余规则和传递规则，我们得到NL系统(对应于带下标★的多模态组合范畴语法)；在保留上述公理和规则的基础上，添加ASS规则，得到L系统(对应于带下标◇多模态组合范畴语法)；在保留上述公理和规则的基础上，添加PER规则，得到NLP系统(对应于带下标×多模态组合范畴语法)；在保留上述公理和规则的基础上，同时添加ASS规则和PER规则，得到LP系统(对应于带下标◎多模态组合范畴语法)。

不同的逻辑系统在进行逻辑推演时，对于能够参与推演的前提所具有的自由程度有不同的要求。据此，我们对传统的范畴类型逻辑系统进行扩展，获得多模态范畴语法的句法推演规则和框架语义解释如下：

Ⅰ.句法部分

F∷ =A|F/iF | FiF | F ·iF | F/jF | FjF | F ·jF |

特别定义i-范畴集CATi：(这里把F/iF和FiF 和部分F ·iF提出来)

上述定义说明：1)由i-斜线算子为主联结词的函子范畴是i-范畴；2)A和B都是i-范畴且二者不相同，则A ·iB是i-范畴；3)若

A是i-范畴，则A ·iA是i-范畴。

公理和结构公设：

等同公理

M：A ·iAA这里ACATi

合并公设

S：A ·jBA ·iB

关联公设

通常的冗余规则和传递规则：

据等同公理和冗余规则可以推出如下定理：

(4)C/iB ·iBC

(5)A·iAiCC

(6)C/jB ·jBC

(7)A·jAjCC

Ⅱ.语义解释

1.框架限制：

2.语义解释(对两类斜线算子和积算子分别定义)：

v(A ·iB) = {x |yz[Rixyz & yv(A) & zv(B)]}

v(A/iB) = {y |xz[Rixyz & zv(B)xv(A)]}

v(A ·jB) = {x |yz[Rjxyz & yv(A) & zv(B)]}

v(A/jB) = {y |xz[Rjxyz & zv(B)xv(A)]}

三、汉语形名结构中的虚化成分“的”

邹崇理等学者在范畴类型逻辑的框架下，对自然语言中的虚化成分进行了探讨，“的”与英语中的系动词be被视为具有同样句法语义表现的成分*Zou Chongli, Li Kesheng, Zhang Lu, The Categorial Logic of Vacuous Components in Natural Language, eds. by Hans van Ditmarsch etc., Logic, Rationality, and Interaction, Third International Workshop LORIIII Processdings, 2010, pp. 370-381.。在汉语言学界，对“的”的英文翻译不一而论，有“form word”以及“vacuous component”等。从其对应的翻译就可以看出，“的”一方面具有助词(form word)的句法功能，另一方面具备空语义成分(vacuous component)的特征，因此在现代语言学领域，我们常常将其称为“虚化成分”。虚化成分在语言中普遍存在，比如汉语中的“的”以及一些介词性的成分，英语中的系动词等等。对于语言中的介词词组，按照传统的形式化处理方法，我们可进行如下的语义刻画：

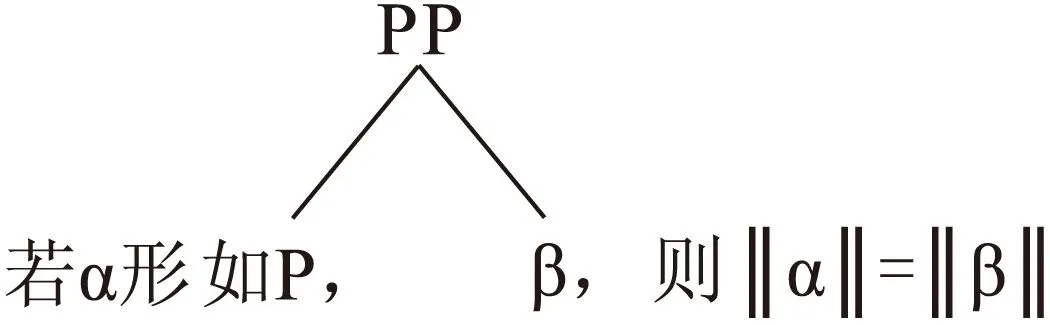
图1　虚化成分的形式语义解释

算，我们就能够得到形名结构的语义。因此，邹崇理认为，对于这类在句法上占据一定位置，而语义上没有表现的语言成分，可以在语义运算之初就构造一个三元范畴，令其在语义推演的开始就被消去，不必参与运算。因此，邹崇理等人采用的做法是引入一个三元的复合范畴[A{B}C]，由其中的B代表自然语言表达式中的虚化成分。通过给出其相应的意义公设，能够构建范畴类型逻辑的系统LMP，这一逻辑系统的主要特征表现为一方面允许虚化成分在句法上出现，另一方面又不必使其参与语义的推演运算过程。

显而易见，这种处理方法是上下文自由的，也就是说，对逻辑推演的前提是不敏感的。规则的增加降低了系统的普遍性，能够刻画英语sweetgirl和汉语“可爱少女”的语法体系，却无法顺其自然地处理“可爱的少女”，这显然不符合人们使用语言的直觉。在自然语言的实际应用中，我们需要对能够被消去的成分进行考察，并不是所有的“的”都能被处理为虚化成分，因此，为了进一步精确的刻画汉语中形名修饰结构中的“的”字结构，我们需要对范畴语法进行弱上下文敏感的扩张，通过控制能够参与推演的前提，实现对语言事实更精准的刻画。

因此，基于多模态范畴语法，汉语虚化成分“的”可以被处理为恒等函项。据此能够使表达式“可爱的”获得与“可爱”同样的句法范畴及其语义词项。以“可爱的少女”作为例子：

(1) a.

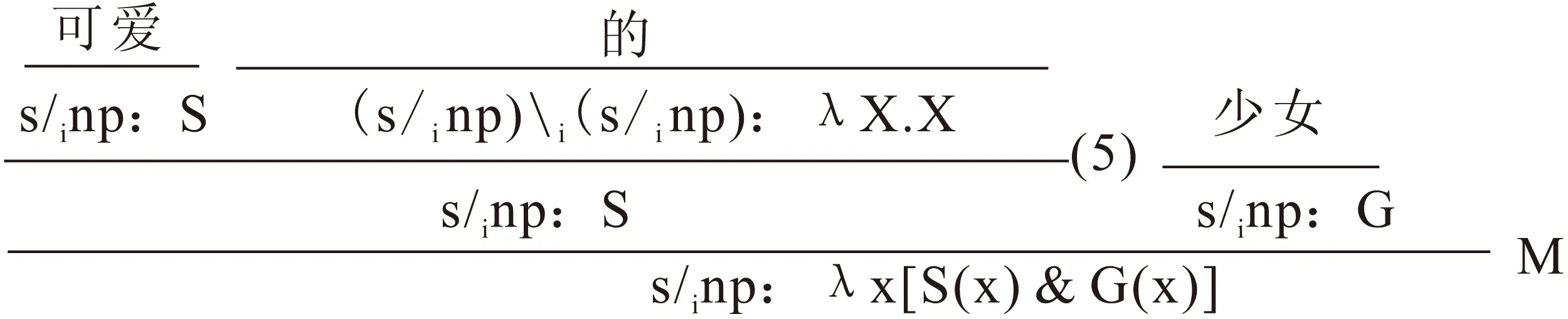
也可以运用M规则直接生成“可爱少女”的推演：

b.

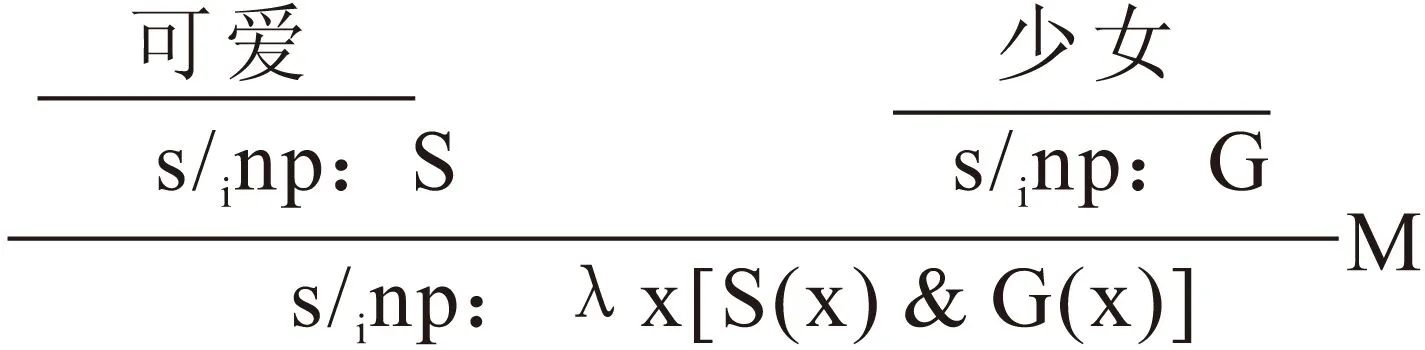
如果尝试进行英汉对比，不难发现，英语普通形名结构与汉语中不带“的”字的形名结构的分析相同，比如sweetgirl具有与“可爱少女”相同的推演：

(2)

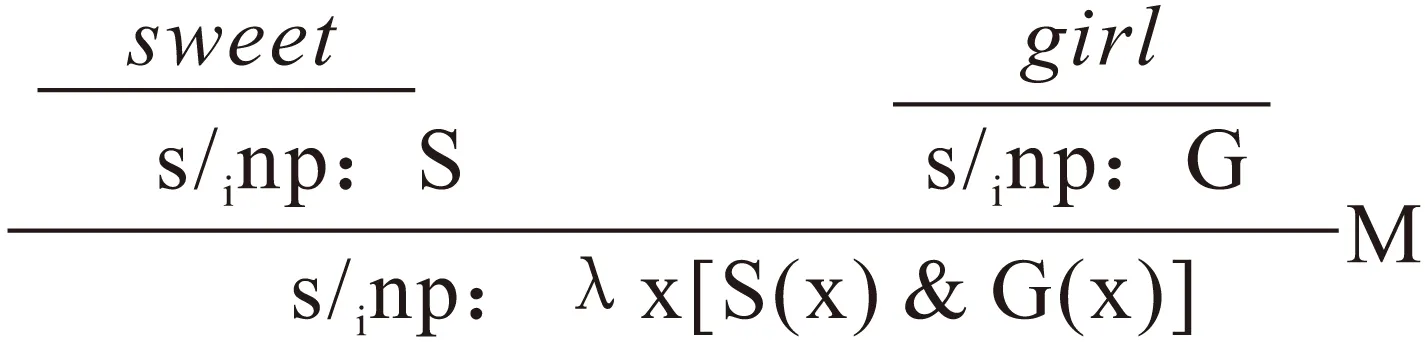
这表明，多模态范畴语法能够揭示英汉形名结构中的相同之处。而仅仅通过将虚化成分“的”处理为恒等函项的方式，我们又能够揭示汉语中带“的”的形名结构和英语的差异。本文仅对汉语中一类形名结构中“的”进行了处理，而语言中还有一类对应“类型函项贴合”的形名结构，比如“典型的错误”，涉及这类形名结构中“的”字的处理，则需要使用多模态范畴语法中的关联规则，此处不再过多讨论。

四、结　语

汉语虚化成分“的”能够被处理为恒等函项而进行消除，原因在于，在某些情况下，带有“的”的自然语言表达式具有与不带“的”的自然语言表达式十分类似的句法结构与完全相同的语义解释。自然语言中存在大量必须使用“的”的场合，这就促使研究者们思索如何能够使用统一的手段，对句法表现类似的结构进行求同并且存异的充分刻画，以满足当前计算机处理自然语言信息的需要。多模态范畴语法无疑是应运而生的产物。多模态范畴语法，作为范畴语法的新发展，将多模态组合范畴语法的前提敏感特征带入了范畴类型逻辑，使得我们能够借助范畴类型逻辑系统对自然语言现象进行更为准确的刻画，多模态范畴语法在处理汉语方面有着独到的优势。

ZHANG Lu, lecturer of School of Foreign Studies, China University of Mining and Technology, Xuzhou, Jiangsu, 221116.

责任编校：余沉

Multi-modal Categorial Grammar and a Study of “de” in Chinese

ZHANG Lu

Categorial Grammar is a logical system which aims at a computable approach toward natural language processing. In the 1970s, Montague Grammar was employed in the analysis of English fragments according to the correspondence between syntactic category and semantic type. From then on, Categorial Grammar has experienced rapid development. Nowadays, Multi-modal Categorial Grammar devours different systems of Categorial Type Logic, aiming at a better combination of these systems in dealing with natural language. The vacuous component “de” in Mandarin Chinese is applied to illustrate the development of Multi-modal Categorial Grammar.

Multi-modal Categorial Grammar; Hybrid Categorial Type Logic; vacuous component “de”

10.13796/j.cnki.1001-5019.2016.05.007

B81

A

1001-5019(2016)05-0048-06

教育部人文社科青年项目(14YJCZH209)

张璐，中国矿业大学外国语言文化学院讲师，逻辑学博士(江苏 徐州221116)。