实现实时套刻对位的仿射变换最优匹配参量计算公式

刘子强，雷 亮，刘 新，王 崎，颜润明，周金运



实现实时套刻对位的仿射变换最优匹配参量计算公式

刘子强，雷 亮，刘 新，王 崎，颜润明，周金运

( 广东工业大学物理与光电工程学院，广州 510006 )

本文讨论了对一般目标图像的对准方法，采用仿射变换模型，舍弃借助迭代法搜索图像最佳配准参数的传统方式，使用推导公式一步计算图像的平移旋转参数。该公式运用仿射变换单应矩阵最小二乘运算模型推导所得，首次得到可单步计算目标图像与待对准图像对位参数的计算算法，大大提高运算效率，实现了实时对位的功能，最后通过实验验证算法的有效性。

图像对准；仿射变换；平移；旋转；单应矩阵

0 引 言

在光刻领域中，光刻投影物镜、掩模硅片对准系统、激光定位工件台并称为投影光刻机的三大核心部分[1]。对于高密度的印刷电路板布线或者集成电路芯片，需要进行套刻曝光，而套刻精度取决于掩模硅片对准系统的对准精度。如图1，以投影光刻系统为例，系统中的平移台与硅片基板之间的支承部件是具有、D、D三个自由度的数控三维微调对准装置①，该装置实现套刻的过程需要使用图像匹配技术。图像匹配是在同一场景中采集到的两幅图像，分别为CCD1拍摄的目标图像②、CCD2拍摄的待对准图像③，提取出角点信息后，根据获取的信息将待对准图平移旋转匹配目标图像的过程，隶属于光电图像处理中控制点仿射变换模型，寻求控制点仿射变换的快速匹配运算算法，在机器视觉和模式识别等相关领域有重要应用价值[2-4]。其中，④~⑥分别是投影光刻系统中的投影系统、照明系统和准分子激光器。

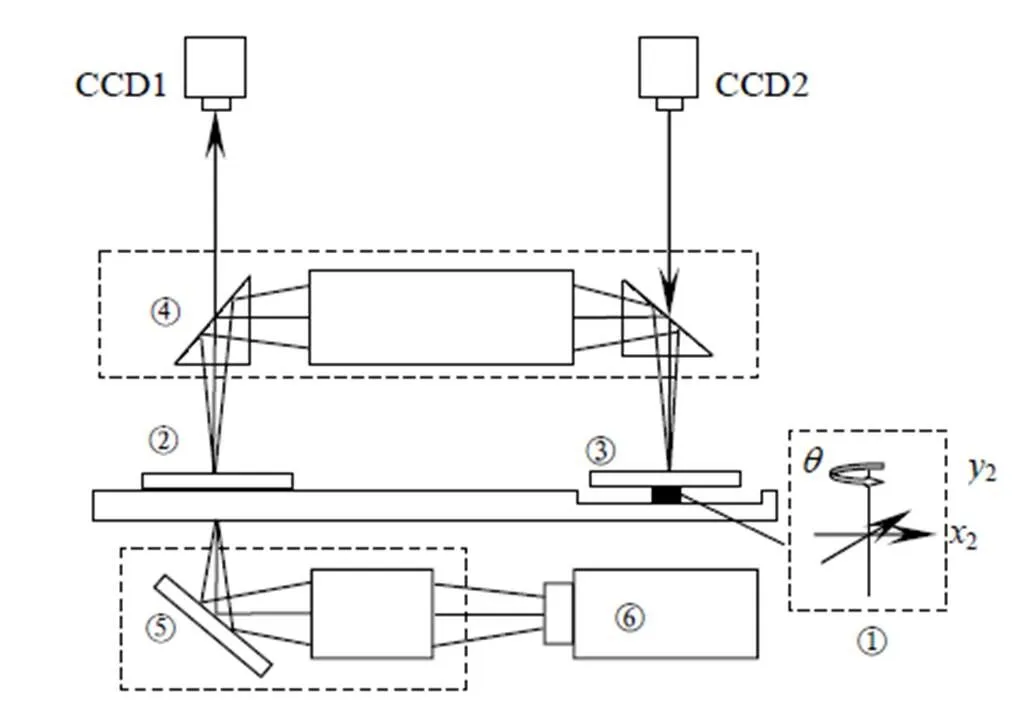
图1 大面积投影光刻系统中的对准实施单元

目前求取仿射变换参数大多都是采用迭代法来求得，需要经过多次迭代求取套刻对位的控制参数，不适用于生产率较高的实时控制型曝光设备。本文首次提出了国内外未见报道的一套求解仿射变换最优匹配参量的计算公式，其核心是基于仿射变换单应矩阵最小二乘运算模型，一步直接计算出最接近理想值的平移旋转参量，以替代传统的Levenberg-Marquardt最小化ML代价函数的迭代过程[5]，在光刻系统上实现了实时对位的功能。

1 仿射变换参量计算

图2和图3为实验过程中需要实现对位的目标图与待对准图。对位算法实施前，需要进行图像二值化、阈值分割、高斯平滑、边缘轮廓提取、角点检测等图像预处理的过程[7-9]。

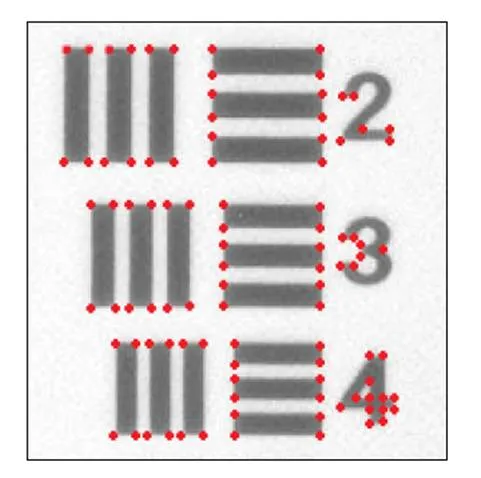
图2 目标图

图3 待对准图

其中角点检测和提取的方法有很多，目前，常用的角点提取算法有Moravec算法、Forstner算法、SUSAN算法、Harris算法和SIFT算法[10]。图2和图3中的点采用Moravec算法提取得到的角点坐标，并将坐标的、分量排列成列矩阵的形式(记“待对准图的角点坐标集”为、；记“目标图的角点坐标集”为、)。以图2、图3为例，角点的数目为=98，则列矩阵为由个整数坐标所组成的单列矩阵，、、如此类推。

于是，可根据上述四个列矩阵以及一个单位列矩阵(由个1排列而成的单列矩阵)，运用如下公式

单步计算得到两幅图像的平移参量D、D、旋转参量。

2 公式推导

式(1)~式(3)是本文的理论核心，运用仿射变换单应矩阵的最小二乘数学模型推导所得，关键的推导过程如下。“待对准图的角点坐标集”中的第个坐标点，旋转角、平移D、D后得到的理想坐标、分别为

记，,，则在(此时在图像坐标系中)情况下式(4)可改写为

于是、与、的距离误差累积函数为

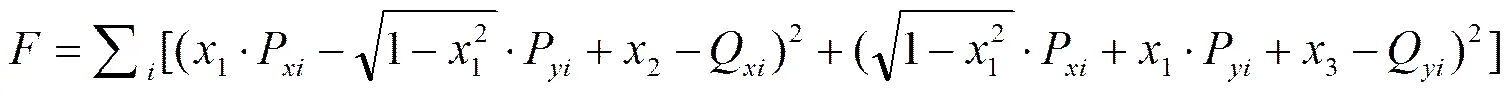
为使所有理想点与对应目标点最接近，令函数对1，2，3的偏导数为零，可衍生得三个方程：

(9)

由此求解得的表达式为

但是，受到“语境”困扰的决不会仅仅是作为“后来者”的读者与研究者。鲁迅本人在写作《藤野先生》《〈呐喊〉自序》时也有着自己的困难——那不是两个主体间的隔阂，而是出于一种叙述上的困境。我们也许可以这样解释这种困境的起因：“人们创造自己的历史，但是他们并不是随心所欲地创造”〔6〕。具体到鲁迅本人，则如董炳月所说，他的叙述(包括正面叙述的和刻意回避的对象)在主观上与他在留日期间的生活状态、以及多年之后的写作意图有关。在客观上也受到记忆的限制。即便鲁迅本人也不能不从叙述行为发生的那个“当下”重新构建一次自己的留学经历。而同时被构建起来的，还有他的叙述行为所包含的价值评判和意义体系。

式(10)在时得式(1)。

式(10)在时依然为式(11)，

无论的求解采用式(1)或(11)，代入式(7)、(8)后皆可求得式(2)、(3)。

3 实验结果

实验上从两方面来验证该算法的有效性。

第一方面：以目标图(图2)为模板图，将图2、图3中提取的角点坐标矩阵代入式(1)~式(3)求取平移旋转参量，所求得的、D、D就是机械控制模块的控制参量，电机控制运转后，待对准图从原来的图3拍摄效果变为如图4的拍摄效果。

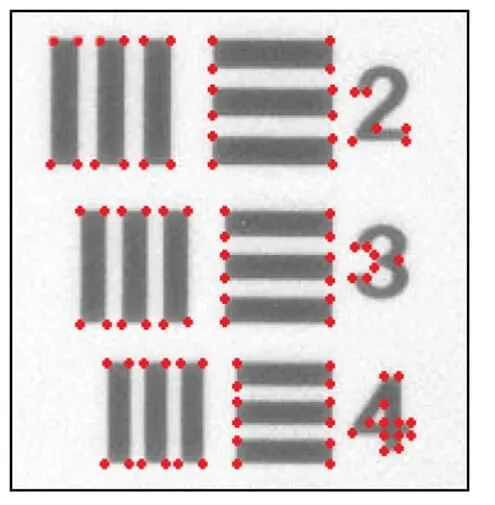
图4 待对准图施行参量控制后的图

比对图2与图4可见，待对准图实施该算法所得到的控制过程后，完全实现了准确的对位。比对的方式是采用两个评价函数定量分析，分别为建立起映射关系的单应角点之间的平均几何距离误差，如式(12)所示alg：

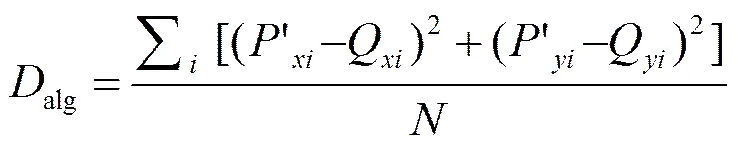
其中：、为“待对准图施行参量控制后的图的角点坐标集”的坐标列矩阵、坐标列矩阵，为角点数目，=1，2，3，…，。

另一个评价函数为施行参量控制后的待对准图与目标图之间的逐点灰度平均误差arv:

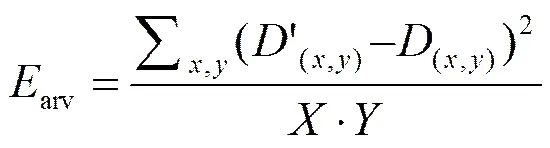
以图2、图3所计算得到=-27.897 7o、D=61.209 3、D=-34.183 5、alg=0.370 5、arv=6，从alg小于1以及arv小于10，从而证明了该算法实现了亚像素级的对位效能。

另外，为证明该算法在各个旋转域的有效普适性，我们从如下的方面实施数值模拟实验：对待对准图旋转任意角度(平移参量D、D为固定值)，求出旋转后的角点坐标矩阵，代入公式求出平移旋转参量，并将求出的参量(1、D1、D1)与输入的参量对比。分别在[-90o，90o)与[90o，270o)两个区间测试(平移参量D、D为固定值时，输出参量D1、D1与输入参量D、D相比基本相等)，测试的结果如图5(a)、(b)所示(为水平轴，1为纵轴)。

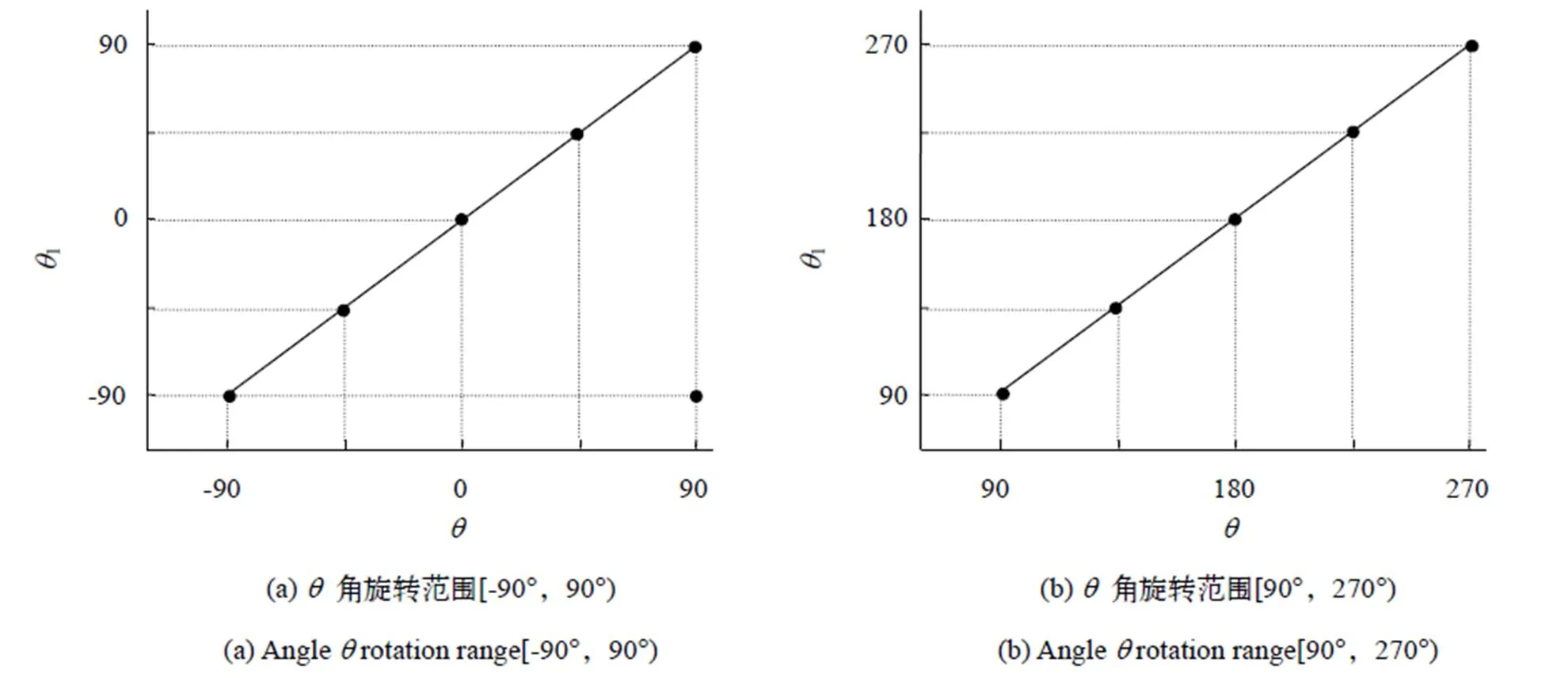
图5 角度旋转前后构成的曲线图

由图5(a)知，输入输出的角度参量、1在坐标轴上呈线性相关(除=90°时的点)，即当在(-90°，90°)范围时，输出参量和输入参量相比均在误差允许范围内(误差为0.1°)，可以说明式(1)~式(3)在此范围内均适用；由图5(b)同样可知，输入输出的角度参量、1在坐标轴上呈线性相关，即当在[90°，270°]范围时，输出参量和输入参量相比均在误差允许范围内(误差为0.1°)，所以式(2)、式(3)、式(11)在为[90°，270°]时均适用。由以上数据分析可得，在各区域范围所求的参量均在误差允许范围内，所以本文提出的公式在均适用。

另从运算时间上看，该组公式算法从开始到得出参数仅需0.081 6 ms的时间(VC6.0编译)，远快于传统迭代方式的运算时间8 ms，验证了该算法的可实时性及效率大大地提高[11]。

4 结 论

本文提出了一种基于仿射变换单应矩阵最小二乘运算模型，直接计算出平移旋转参量的方法，相比传统的迭代运算方法，单步即可求得图像的平移旋转参量，并且通过实验验证了该方法的有效性。在众多需要实时对位的应用领域上，本文提出的方法具有很大的实效优势。

[1] 姚汉民，胡松，邢廷文.光学投影曝光微纳加工技术 [M].北京：北京工业大学出版社，2006：83-129.

YAO Hanmin，HU Song，XING Tingwen. Optical projection exposure micro-nano processing technology [M]. Beijing：BeijingIndustry University Press，2006：83-129.

[2] 雷亮，李浪林，周金运，等. 投影光刻系统中的掩模硅片相关识别对准技术 [J]. 量子电子学报，2012，29(6)：764-768.

LEI Liang，LI Langlin，ZHOU Jinyun，.Correlation recognition and alignment technology of mask in projection lithography system [J]. ChineseJournal of Quantum Electronics，2012，29(6)：764-768.

2.3.1 水提工艺设计 以加水量、煎煮时间、煎煮次数为因素，选用L9（34）因素水平表安排正交试验。见表4。

[3] 王小鹏，房超，雷涛. 一种平移旋转图像的角点匹配方法 [J]. 计算机工程与应用，2014，50(16)：173-176.

WANG Xiaopeng，FANG Chao，LEI Tao. Corner matching method for translation and rotation image [J]. Computer Engineering and Applications，2014，50(16)：173-176.

[4] 陈杭，杜小平，夏鲁瑞，等. 基于控制点的一种高光谱图像配准方法 [J]. 装备学院学报，2013，24(3)：109-113.

CHEN Hang，DU Xiaoping，XIA Lurui，Registration method for hyperspectral image based on control points [J]. Journal of Academy of Equipment，2013，24(3)：109-113.

[5] 刘彬，陈向宁，郭连朋，等. 一种基于多重单应引导的特征点匹配算法研究 [J]. 信息工程大学学报，2013，14(5)：591-595.

LIU Bin，CHEN Xiangning，GUO Lianpeng，Feature Point Matching Algorithm Based on Multiple Homography [J]. Journal of Information Engineering University，2013，14(5)：591-595.

[6] R Hartley，A Zisserman. Multiple View Geomet [M]. Cambridge University Press，2000：416-418.

[7] 江明，刘辉，黄欢. 图像二值化技术的研究 [J]. 软件导刊，2009，8(4)：175-177.

JIANG Ming，LIU Hui，HUANG Huan.Research on binarization image technology [J]. Software Guide，2009，8(4)：175-177.

[8] 龙建武，申铉京，魏巍，等. 一种结合纹理信息的三维Renyi熵阈值分割算法 [J]. 小型微型计算机系统，2011，32(5)：947-952.

LONG Jianwu，SHEN Xuanjing，WEI Wei，. 3-D Renyi Entropy Thresholding Algorithm Combining with the Texture [J]. Journal of Chinese Computer Systems，2011，32(5)：947-952.

[9] 肖茜，鲁宏伟. 基于高斯平滑的自适应角点检测 [J]. 计算机辅助设计与图形学学报，2004，15(11)：1358-1361.

XIAO Qian，LU Hongwei. Adaptive Corner Detection Based on Gaussian Smoothing [J]. Journal of Computer-Aided Design & Computer Graphics，2004，15(11)：1358-1361.

[10] 杨晓晖，王文娟. 图像特征点提取角点量阈值自适应选取方法 [J]. 光学与光电技术，2012，10(5)：72-75.

YANG Xiaohui，WANG Wenjuan.Threshold adaptive selection method for corner detection of image feature points [J]. Optics & Optoelectronic Technology，2012，10(5)：72-75.

[11] 宋麦玲，陈云亮. 基于仿射变换的图象定位方法 [J]. 电脑知识与技术，2007(14)：478-480.

SONG Mailing，CHEN Yunliang. Research on Image Tracking Based on Affine Trans form [J]. Computer Knowledge and Technology，2007(14)：478-480.

Affine Transformation Optimal Matching Parameter Calculation Formula of Real-time Overlay Alignment

LIU Ziqiang，LEI Liang，LIU Xin，WANG Qi，YAN Runming，ZHOU Jinyun

( School of Physics and Optoelectronic Engineering, Guangdong University of Technology, Guangzhou 510006, China)

Trying to provide a more effective algorithm for real-time counterpoint and alignment in the image, we propose an estimate method using affine transformation modal to calculate image translation rotation parameters, which is different from the traditional iteration method in searching image. It’s the first time to provide the algorithm which can calculate target and alignment image registration parameter by single step, using the model of the least square of the affine transformation homography. And the effectiveness of this algorithm is validated through the corresponding experiment.

alignment; affine transformation; translation; rotation; homography

TP391.41

A

10.3969/j.issn.1003-501X.2016.04.010

2015-08-17；

2015-10-08

广州市科技计划项目(2014J4100205、2014J420081)资助课题

刘子强(1992-)，男(汉族)，广东梅州人。硕士研究生，主要研究方向为光电机器视觉。E-mail：822132032@qq.com。

雷亮(1979-)，男(汉族)，广东台山人。副教授，博士，主要从事光刻系统与光电机器视觉研究。E-mail: leiliang@gdut.edu.cn。