恰当进行教学设计减轻学生认知负荷

刘丹+王光明�オ�

【摘要】近年来认知负荷理论逐渐在教学领域，尤其是在教学设计方面，产生越来越重要的影响.教学设计不能对内在认知负荷产生直接的影响，既即使是恰当的教学设计也不会对其产生影响.但是教学设计可以改变外在认知负荷和相关认知负荷，这两种认知负荷的产生，与教学设计的恰当与否有直接关系.本文在教学设计方面所指的认知负荷皆指外在认知负荷量和相关认知负荷量的总和，以《弧、弦、圆心角》为例，分析当前不恰当的教学设计在增加学生认知负荷方面的问题，据此提出如何进行恰当的教学设计，进而减轻学生的认知负荷，即运用切割分行或符号标志技术等呈现定理新形式、对多种形式进行整合、重视小结环节.本文提出的教学设计方式对数学其他方面的教学设计具有一定的启发作用.

关键词外在认知负荷；相关认知负荷；教学设计；定理新形式；课堂小结1认知负荷理论及其对教学设计影响

认知负荷理论（Cognitive Load Theory）[1]是由澳大利亚心理学家约翰·斯威勒（John Sweller）于1988年首次提出并加以发展的一种理论.认知负荷是指同时被要求施加在工作记忆上的智力活动的全部数量，即工作记忆必须加以注意和进行处理的所有内容.在分析信息结构与认知结构关系的基础上，认知负荷理论提出信息加工过程中施加在工作记忆上的三种认知负荷类型：内在认知负荷、外在认知负荷和相关认知负荷[2].近年来认知负荷理论逐渐在教学领域产生越来越重要的影响.

已有研究表明[3-6]，内在认知负荷的高低与材料本身的复杂程度和学生的知识水平有关，教学很难控制和改变它.外在认知负荷主要由材料中信息的组织和呈现方式决定，这种信息的组织和呈现方式与教学设计有关，教学设计不当会增加外在认知负荷.相关认知负荷是指工作记忆对学习任务进行实质性认知而承受的负荷，实质性认知是指与形成图式建构与图式自动化密切相关的活动[7].认知负荷理论认为，学习即是图式的获得或图式加工达到自动化的过程，因此提高相关认知负荷促进学习的发生，对于教学来说也尤为重要[8].由此看来，教学不能对内在认知负荷产生直接的影响.但是教学可以改变外在认知负荷和相关认知负荷，这两种认知负荷的产生，与教学设计的恰当与否有直接关系.

在教学设计中，没有相应的实践技术将外在认知负荷和相关认知负荷区别开来，我们只能决定认知负荷总量[9].认知负荷理论致力于探索教学设计如何减少外在认知负荷这一问题.近年来，一些研究又发现，当教学设计进行教学图式建构时，相关认知负荷便会增加.这类研究的基本主张是：教学程序的科学性决定相关认知负荷的高低，教学设计应当通过鼓励学生参与同图式建构直接关联的有意识的认知加工活动来进一步改善认知负荷总量.另外，越来越多的研究以认知负荷理论为基础，探究如何在教学设计过程中降低学生的认知负荷总量[10，11].基于很多研究认知负荷量作为外在认知负荷和相关认知负荷的二者之和.因此，本文所述认知负荷也指外在认知负荷量和相关认知负荷量的总和.

一些研究发现目前的教学设计存在良莠.有助于减轻学生认知负荷的教学设计是良好的教学设计，反之是不佳的教学设计[10，11].也即不恰当的教学设计会增加学生的认知负荷[12]，恰当的教学设计会减少学生的外在认知负荷、增加相关认知负荷，即降低认知负荷总量，使学生合理地利用有限的认知资源，达到最好的学习效果[8].本文拟基于认知负荷理论的视角，以《弧、弦、圆心角》为例，分析当前不恰当的教学设计在增加学生认知负荷方面的问题，然后据此提出如何进行恰当的教学设计进而减轻学生的认知负荷.

2不恰当的教学设计会增加学生认知负荷

目前，一些学校对教师教案的例行检查流于形式，实效性较差，使得教师不重视教学的设计，这在一定程度上影响教学效果的提升[13].另外，许多研究过分关注教师应该如何教才能有效[14].在教育教学过程中也出现同样的问题，从一些教学设计中分析出，很多教师是从自身的角度出发，考虑如何对这一节课进行教学才能有效率并且有效果，这样的教学设计注重教师的教而忽视学生的学[15-17].然而，学生是有意识的，是学习和认识的主体，教师并未考虑到学生的认知能力，很多环节的设置增加了学生的认知负荷，给学生造成了不必要的学习负担.《弧、弦、圆心角》是新人教版九年级数学第二十四章圆的一节重要课程，下面以这一节课中的关系定理为例，分析当前数学教学设计在增加学生认知负荷方面的问题.

2.1案例——“弧、弦、圆心角关系定理”的教学设计

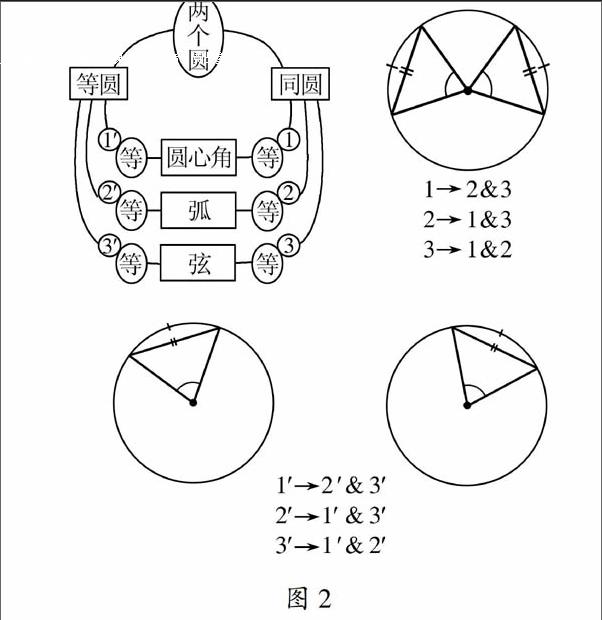
《弧、弦、圆心角》这节课中，其中圆心角、弧、弦关系定理是本节课教学的重点内容，对定理中的“在同圆或等圆”条件的理解是教学的一个难点.在已有的教学设计过程中，教师利用圆的旋转不变形突破教学重点，通过举反例来解决教学难点，具体教学过程包括以下几个方面：

（1）通过实验，利用圆的旋转不变性，引导学生得到弧、弦、圆心角关系定理，让学生在定理的空白处填空或者教师直接板书：在同圆或等圆中，如果两个圆心角相等，那么它们所对的弧相等，它们所对的弦也相等.（2）在该关系定理中，教师强调“在同圆或等圆”条件的重要性，并通过举出反例加深学生对定理的理解：“如果不加‘同圆或等圆这一条件，定理中的结论是否成立？”（3）教师引导学生得到弧、弦、圆心角关系定理的推论并板书，或是直接给出该定理的推论：在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角相等，所对的弦相等；在同圆或等圆中，如果两条弦相等，那么它们所对的圆心角相等，所对的弧相等.在“同圆或等圆中”这个前提下，将题设和结论中任何一项交换都是正确的.（4）再通过例题巩固学生对弧、弦、圆心角关系定理及其推论内容的学习.（5）最后是对本节课的小结，总结本节课所学的定理的内容及所用到的思想方法.

2.2教学设计存在的问题分析

上述教学设计中，几处环节设置并不符合认知负荷理论的观点，例如：一连串的定理呈现方式、定理及其推论呈现形式单一、小结环节设置不当等，这些设计都不利于降低学生的认知负荷.

2.21定理的呈现方式

在《弧、弦、圆心角》这节课中，教师将关系定理以如下的方式呈现给学生：

在同圆或等圆中，如果两个圆心角相等，那么它们所对的弧相等，它们所对的弦也相等.

这种一连串的定理呈现方式传送大量的信息到学生眼前，但是从认知负荷角度来看，有效学习不一定能够发生，即学生不一定能够获得学习图式或图式的加工不一定能够达到自动化的过程.认知负荷理论提出的“冗余效应（Redundancy Effect）”[18]要求呈现给学生的必须是剔除了冗余信息的核心教学内容.这里有很多信息与该定理中的核心内容无关，属冗余信息，这种教学设计就导致了认知负荷的增加，给学生带来了学习该关系定理的负担.

2.22复杂的内容呈现形式单一

知识是复杂的，教学过程具有交互性.对于复杂的知识，单纯的文本呈现方式已经不能很好地降低认知负荷.然而在不同的外部呈现方式之间寻找关联性，同时搜索并注意大量的信息，会产生“注意力分散效应（Split—Attention Effect）”，影响图式的获得，增加学生的认知负荷[19，20].这就需要在教学过程中整合多种呈现方式，通过增加相关认知负荷以减少认知负荷总量，这对提高教学的有效性是非常重要的.弧、弦、圆心角关系定理及其推论的内容比较复杂，但是教师只是以单一的文字形式将这些内容呈现给学生，并未将文本、图表或是表格多种呈现方式相互补充、相互整合地呈现给学生，这不利于降低学生的认知负荷.

2.23忽视小结环节

有研究表明[21，22]，课堂小结几乎是每节课必不可少的环节.小结是课堂教学的升华，是课堂有效性教学的点睛之笔.然而由于教学内容复杂，教学时间紧迫等原因，课堂小结往往被忽视.在小结环节如果运用图表、口诀等形式，条理清晰，能够便于学生记忆.有的教师会认为图表、口诀会给学生造成不必要的负担，其实不然，这些形式可以通过合理地构建认知图式降低学生的认知负荷.一些教学设计从小结的内容和方式来看显得流于形式，缺乏实际内容因而没有多少意义和价值[23].上述教学设计中，教师对小结环节也只是一笔带过，并未重视该环节.3恰当的教学设计会减轻学生的认知负荷

既然一些教学设计环节增加了学生的认知负荷，那么本文提出的恰当的教学设计就应该始于“学生的认知”，终于“降低学生的认知负荷”.通过以下教学设计，使减轻学生的认知负荷成为可能.

3.1呈现定理新形式

在表达方式方面，将定理及其推论的表述方式进行分行、切割，并将定理及其推论中的关键词涂上颜色，以区别于冗余信息；在配图方面，将圆形中的无关要素虚化.这在一定程度上剔除了弧、弦与圆心角关系定理的冗余信息.

3.11切割、分行

以往的教学设计过程中，教师将定理以一连串的形式呈现给学生，学生要花更多时间来阅读，这会降低对关键内容的学习.恰当的教学设计考虑对定理进行总结概括，总结概括的方式包括：切割、分行，以突出其中的重要内容，而不是把它以呆板的一连串文字的形式呈现出来.

3.12运用符号标志技术

符号标志技术是指突出文本的内容或结构而没有增加文本内容的写作技术[24]，例如印刷格式中出现的有色字体、下划线、黑体等.符号标志虽不增加具体的内容，但可以使材料的结构更为清晰明了，这十分有利于读者形成对教材内容连贯的表征.B.J.F.Meyar、R.E.Mayer、N.L.Loman等人都做过一组对比试验，两组学生分别阅读有符号标志和没有符号标志的文章，结果发现阅读有符号标志文章的学生对于文章中的逻辑关系掌握的更好[25].符号标志技术促进学生掌握教材中的逻辑关系.恰当的教学设计过程中不能黑压压地呈现出一段定理及其推论，可以运用这种符号标志技术，综合运用有色字体、变化的字体手段厘清所要呈现出的内容的内在联系.在弧、弦、圆心角关系定理中，对于关键的信息就可以利用不同的颜色，以区别于其他信息.

3.13虚化无关要素

F.M.Dwyer曾做了一个实验，让四组大学生学习人的心脏解剖结构.结果发现，第二组学生观察的心脏各部位具有轮廓图，学习效果最佳；而其他组学生学习的材料中并没有突出心脏各部位的轮廓图.轮廓图突出了心脏的关键特征，消除了无关特征，产生最佳的学习效果[26].通过缩短图形元素的搜索时间可以降低外在认知负荷[27].可将这两个研究的结论运用在弧、弦、圆心角关系定理教学中，运用几何图形对文本进行说明时，要虚化无关要素以消除无关特征、突出图形中要传递信息的关键特征、缩短对关键特征的搜索时间，这样可以降低外在认知负荷，使学生产生最佳的学习效果.

综合以上三点设想，设计出弧、弦、圆心角关系定理新的结构，如下：

3.2整合多种形式

3.21图表

对于难度较大的复杂教学内容，图表在减轻认知负荷方面也可以起到有效的作用.因为图表可以激活和利用学生大脑中的认知图式，从而增加相关认知负荷以减少认知负荷总量，学生只要在工作记忆中操作少数信息元素就可以进行有效的学习.特别是在新手学习的起始阶段，大脑中还没有形成学习新知识的基本图式，这就需要图表来帮助他们形成一定的认知支架.J.Sweller等人的研究还发现几何教科书如果能将图表和相应的文字材料整合在一起，让学生能同时注意到，则可以降低认知负荷，从而促进学习效率的提高[28].从这项研究中也能看出图表对教学设计的重要性.

弧、弦与圆心角关系定理可采用分行切割的形式呈现，但是该定理与其推论的内容放在一起对初学者来说属于复杂的内容，这样就可以用图1来呈现.图1