面向用户行驶计划的电动汽车充电调度策略

曾鸣　冷甦鹏　张科

摘要：充电站（桩）尚未普及以及电动汽车有限的行驶里程，使得大多数汽车用户关于是否选择电动汽车犹豫不决。为了减少用户对于电动汽车有限电池容量的担心，并且降低因频繁充电以及偏离原定行驶路线绕路进行充电所增加的电动汽车使用费用，提出一种基于匹配理论面向用户行驶计划的电动汽车充电调度方案TPCS。首先，分别根据电动汽车用户的行驶计划和对各充电站的电量需求构建电动汽车用户与充电站的偏好表；然后，建立电动汽车用户与充电站之间的多对一匹配模型；最后，以系统总效用为优化目标进行充电站接口分配。数值仿真结果显示，与随机分配（RCS）算法和仅考虑电动汽车效用分配（OEVS）算法相比，TPCS算法将系统总效用较RCS算法最多提高了39.3%，较OEVS算法最多提高了5%；而在电动汽车充电需求轻负载时，TPCS算法始终保证用户满意度在90%以上，高于RCS算法。所提算法能够有效地提高系统总效用和用户满意度，同时降低计算复杂度。

关键词：充电调度；行驶计划；车辆入电网；匹配理论；偏好表

中图分类号：TP393.07

文献标志码：A

0引言

近年来电动汽车（Electric Vehicle， EV）的低碳环保性和经济实用性使得电动汽车在汽车市场中的比例逐步上升，由电动汽车充电带来的大规模用电需求若不经过合理的充电调度，将大幅增加现有电网的电力负担[1]。此外，对于行驶模式下的电动汽车，频繁地充电与绕路充电都会影响电动汽车使用者的用户体验。

目前国内外研究大多将电动汽车与智能电网这一研究热点相结合，旨在利用调度电动汽车充电调节电网的峰谷值差。文献[2]考察了充电方案和充电速率对某一特定住宅楼的电网负载情况的影响；文献[3]研究了风能作为电网能量来源时电动汽车的充电调度问题，文中考虑了风能的不确定性与动态变化及电动汽车的停泊时长，利用马尔可夫决策过程对问题进行了建模；在文献[4]中，充电站之间互相竞争形成非合作博弈，以提高配电网络的稳定性和充电站的收益为目标制定电动汽车的充电站选择策略；文献[5]以二次函数建模电网网损，以最小化网损为优化目标；文献[6]研究在电动汽车需在某一截止时间前充满电的约束条件下最小化电网的峰值负荷；文献[7]通过控制电动汽车的充电行为减少大规模电动汽车充电对电网的影响，同时也减少了电网网损。以上关于电动汽车充电调度问题的研究均未在以减小电网峰均比为优化目标的同时考虑用户行驶计划对电动汽车用户选择充电站的影响。

本文运用基于效用函数的匹配理论框架[8]，考虑行驶模式下电动汽车的行驶计划，将电动汽车充电调度问题建模成一个带双边偏好的多对一匹配问题，设计了面向用户行驶计划的电动汽车充电调度（Traveling Plan-aware Charging Scheduling， TPCS）算法，比较在考虑电动汽车行驶计划的情况下，系统效用函数和电动汽车使用者满意度的变化情况。

1系统建模

如图1所示，假设N个充电站（Charging Station， CS）和M辆需要充电的电动汽车（Electric Vehicle， EV）分布在考察的道路区域内。每个充电站可同时最多提供个充电接口为充电汽车进行充电。每个充电接口的充电速率假Ki（i=1，2，…，N）定为不变的，且各充电站各充电接口的充电速率一致。

电动汽车选择充电站通常有自己的偏好。一般来说，首先，电动汽车的使用者通常希望充电站在其之后行驶路线的沿路上，而无须开车绕路去充电。其次，充电站所在的位置需满足该电动汽车当前剩余电量可达的条件，否则电动汽车无法抵达充电站。再次，根据用户的行程安排，通常对于充电完成时间会有所要求。比如，电动汽车的行程安排为上午11点之后会去到比较偏远暂时还没有布设充电站的区域，用户会要求充电过程必须在上午11点之前完成。

其中：p为充电站向电动汽车收取的充电单价，本模型中假设各充电站向需要充电的各电动汽车收取相同的充电单价。因此，为了最大化效用函数，各充电站会优先选择请求充电量大的电动汽车为其提供充电服务。

令Ω表示分配矩阵，其中矩阵元素aij={0，1}，aij=1表示充电站i被分配给电动汽车提供充电服务，aij=0表示充电站未被分配给电动汽车提供充电服务。令β为电动汽车效用函数与充电站效用函数之间的权重参数，在本文所建立的优化模型中，同等对待充电桩的效用与电动汽车的效用，因此将权重参数β设为1。实际应用中，若从充电站运营的角度出发，可以将充电站的权重系数增大，但同时也应适当考虑充电电动汽车的效用，需要根据实际应用场景权衡电动汽车与充电站两者之间的效用，在不同应用场景下选取恰当的权重系数。

以上电动汽车与充电站之间的匹配问题的优化目标为最大化系统总效用，因此考虑电动汽车行驶计划的充电调度优化问题可建模为：

2.2算法求解

电动汽车集合与充电站集合为两个不相交的集合，因此本文将为电动汽车分配充电站的优化问题映射为多对一的匹配问题。文献[8]中提出了用于求解一对一匹配的接收延迟算法，本文将该算法扩展到为电动汽车分配充电站的多对一匹配问题中。

第一阶段：首先，每辆电动汽车通过GPS信号获得行驶计划中可能途经的充电站的位置信息，根据到达这些充电站的路程信息、当前电池的剩余电量以及行驶计划中的时间安排按照式（1）计算在各充电站处充电能够获得的效用值。其次，按照式（1）计算每辆电动汽车的效用值，并以降序排列的方式将效用值为正的充电站放入相应电动汽车的偏好表中。

第二阶段：首先，每辆电动汽车同时向在其偏好表中排名第一的充电站，即电动汽车行驶计划中途经的充电站中用户最希望去充电的充电站，发出充电请求。各充电站收到这一轮的充电请求后，检查收到充电请求数目的多少，若多于充电站现有空闲充电接口数目，则选择请求充电量较大的Ki个充电请求，缓存下这Ki个充电请求的电动汽车编号和充电请求电量，并向其他电动汽车发送拒绝其充电请求的消息。若充电请求的数目少于Ki，则将这一轮所有发送充电请求的电动汽车的编号和充电请求电量缓存下来。

第三阶段：收到拒绝充电请求消息的电动汽车向其偏好表中的次优充电站发送充电请求。收到充电请求的充电站将本轮收到的充电请求和上一轮缓存的充电请求进行比较，从中选出请求充电量较大的Ki个充电请求，并缓存其电动汽车编号和充电请求电量。依此循环，直至所有充电站的缓存集合的并集等于电动汽车的集合或者未在充电站缓存集合中的电动汽车已被所有充电站拒绝，循环结束。

3性能仿真分析

仿真场景为50km×50km的区域内有10个充电站随机分布，每个充电站有10个充电接口；4种单位行驶距离需要消耗不同电量的电动汽车发出充电请求[11]；电动汽车到充电站的路程服从均匀分布U（0，30]km；电动汽车的充电请求电量服从均匀分布U（10，20]kWh；充电完成时间晚于截止时间的概率为0.2；延迟代价常数C=100。本文所建立的优化模型中假定若电动汽车预计到达某充电站的时刻晚于该电动汽车行驶计划中期望抵达此充电站的最晚时刻，则放弃在此充电站进行充电。因此，将C设为100使得根据式（1）计算的电动汽车若在此充电站进行充电得到的效用值为负。C还可以根据其他准则来选取，例如，如果电动汽车预计到达某充电桩的时刻晚于行驶计划中规定可以到达该充电桩的最晚时刻，依然将该充电桩放入其偏好表中，则C可小于100。

为了便于比较，仿真实验结果中加入了随机分配（Random Charging Scheduling， RCS）和仅考虑电动汽车效用分配（Only utility of Electric Vehicle concerned Scheduling， OEVS）的两种方案。

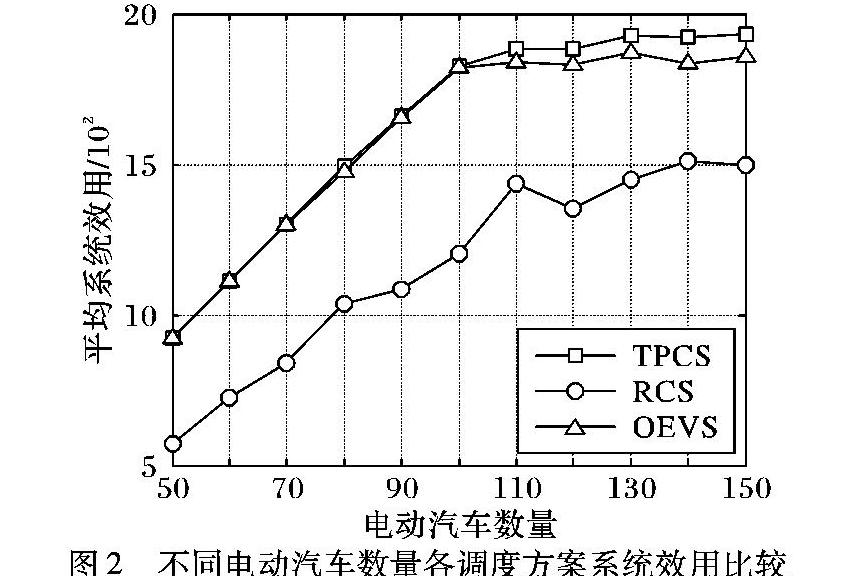
图2给出了三种调度方案下的系统效用随电动汽车数量变化的变化情况。相比RCS和OEVS调度方案，TPCS调度方案可以获得最大的系统效用。当电动汽车数目小于等于100辆时，TPCS算法获得的系统效用与OEVS几乎相当，均高于RCS算法获得的系统效用；当电动汽车数目为120辆时，与RCS算法相比，采用TPCS算法系统效用提高了39.3%；当电动汽车数目增至140辆时，与OEVS算法相比，采用TPCS算法系统效用提高了5%。

图3给出了随电动汽车数量变化不同调度方案下电动汽车充电满意度的变化情况。当电动汽车的数量少于110辆时，TPCS调度算法和OEVS调度算法均能保证电动汽车充电满意度在90%以上，远高于RCS调度算法；当需要充电的电动汽车的数量大于110辆时，由于充电站和各充电站能够提供的充电接口有限，三种调度方案下的电动汽车充电满意度都急剧下降。

图4给出了TPCS调度方案下迭代次数与充电站个数的关系。给定电动汽车的数量M，TPCS算法的迭代次数先随充电站个数的增加而增加，然后随充电站个数的增加而减少，迭代次数的最大值在电动汽车数量与所有充电站可提供的充电接口总额相近时取得。这是因为当电动汽车数目远小于所有充电站可提供的充电接口总额时，即充电请求轻负载时，循环结束条件“未在充电站缓存集合中的电动汽车已被所有充电站拒绝”易被满足进而循环结束；当电动汽车数目远大于所有充电站可提供的充电接口总额时，即充电请求重负载时，循环结束条件“所有充电站的缓存集合的并集等于电动汽车的集合”易被满足而导致循环结束。从图4也可以看出，迭代次数并未以指数级增长，因此该算法的计算复杂度在可接受范围内。

4结语

本文对考虑了电动汽车用户行驶计划的电动汽车充电调度问题进行了建模，运用匹配理论提出TPCS算法对优化问题进行求解。通过仿真实验验证了在TPCS调度方案下，相比RCS和OEVS调度方案，系统效用和电动汽车用户的满意度均有提升，且该算法具有可接受的计算复杂度。该研究结果能够通过设计电动汽车调度算法帮助提高现有充电站充电负载能力，并且提升用户使用电动汽车的满意度。后续研究可以进一步考虑构建电动汽车用户偏好表时的其他影响因素。

参考文献：

[1]BARI A， JIANG J， SAAD W， et al. Challenges in the smart grid applications： an overview [J]. International Journal of Distributed Sensor Networks， 2014， 2014： Article ID 974682.

[2]VAN ROY J， LEEMPUT N， GETH F， et al. Apartment building electricity system impact of operational electric vehicle charging strategies [J]. IEEE Transactions on Sustainable Energy， 2014， 5（1）： 264-272.

[3]HUANG Q， JIA Q-S， QIU Z， et al. Matching EV charging load with uncertain wind： a simulation-based policy improvement approach [J]. IEEE Transactions on Smart Grid， 2015， 6（3）： 1425-1433.

[4]TAN J， WANG L. Real-time charging navigation of electric vehicles to fast charging stations： a hierarchical game approach [J]. IEEE Transactions on Smart Grid， 2015， 8（1）： 1-11.

https：//www.researchgate.net/publication/280924799， IEEE网站提供的就有问题？

[5]CLEMENT-NYNS K， HAESEN E， DRIESEN J. The impact of vehicle-to-grid on the distribution grid [J]. Electric Power Systems Research， 2011， 81（1）： 185-192.

[6]ZHAO S， LIN X， CHEN M. Peak-minimizing online EV charging： price-of-uncertainty and algorithm robustification [C]// INFOCOM 2015： Proceedings of the 2015 IEEE International Conference on Computer Communications. Washington， DC： IEEE Computer Society， 2015： 2335-2343.

[7]VERZIJLBERGH R A， GROND M O W， LUKSZO Z， et al. Network impacts and cost savings of controlled EV charging [J]. IEEE Transactions on Smart Grid， 2012， 3（3）： 1203-1212.

[8]GALE D， SHAPLEY L S. College admissions and the stability of marriage [J]. American Mathematical Monthly， 1962， 69（1）： 9-15.

[9]SAAD W， DAWY Z， SHARAFEDDINE S. A utility-based algorithm for joint uplink/downlink scheduling in wireless cellular networks [J]. Journal of Network & Computer Applications， 2012， 35（1）： 348-356.

[10]PANTISANO F， BENNIS M， SAAD W， et al. Match to cache： joint user association and backhaul allocation in cache-aware small cell networks [C]// ICC 2015： Proceedings of the 2015 IEEE International Conference on Communications. Washington， DC： IEEE Computer Society， 2015： 3082-3087.

[11]SEMIARI O， SAAD W， DAWY Z， et al. Matching theory for backhaul management in small cell networks with mmWave capabilities [C]// ICC 2015： Proceedings of the 2015 IEEE International Conference on Communications. Washington， DC： IEEE Computer Society， 2015： 3460-3465.

[12]EL-HAJJ A M， DAWY Z， SAAD W. A stable matching game for joint uplink/downlink resource allocation in OFDMA wireless networks [C]// ICC 2012： Proceedings of the 2012 IEEE International Conference on Communications. Washington， DC： IEEE Computer Society， 2012： 5354-5359.

[13]ZENG M， LENG S， ZHANG Y. Power charging and discharging scheduling for V2G networks in the smart grid [C]// ICC 2013： Proceedings of the 2013 IEEE International Conference on Communications workshops. Washington， DC： IEEE Computer Society， 2013： 1052-1056.