基于C形臂的手术导航相机标定方法

张建法　张峰峰　孙立宁　匡绍龙

摘要：针对基于C形臂的手术导航系统中相机标定这一关键技术中存在的过渡环节过多、参数求解过程复杂等问题，提出一种完全忽略相机模型的解决方法。该方法完全忽略相机模型，在映射参数求解过程中简化了过渡环节，使得算法实现变得高效；同时，提出了带有双层金属球的校准靶，通过识别小球的投影数据来实现相机标定。在校准点验证实验中，可以验证经变换后的坐标的残余误差均不超过0.002像素；在导航验证实验中，借助初步搭建的导航平台成功实现了探针取点及穿孔。实验结果表明，该相机标定方法的精度能够满足手术导航系统的精度要求。

关键词：C形臂；校准靶；实验平台；相机标定；手术导航系统

中图分类号：TP391.7

文献标志码：A

0引言

图像引导手术系统（Image-guided Surgery， IGS）以X线、CT（Computed Tomography）、MRI（Magnetic Resonance Imaging）等医学图像为载体，采用高精度定位系统跟踪手术工具与患者的相对位姿关系，并加以实时虚拟显示，以辅助医生提高手术质量[1]，其拓展了医生的视野，对于提高手术定位精度、减少手术创伤、缩短手术时间等具有非常重要的意义。目前，基于C形臂的手术导航系统因无需进行术前术中配准，可在术中随时现场获取患者解剖图像及可利用当前大多数医院已有的C形臂设备等优点而受到广泛研究，其中相机标定是该系统的关键技术之一。

到目前为止，众多研究者们针对相机校准分别提出了不同的标定方法，其中以文献[2-4]中提出的校准方法较为经典。上述方法均能达到理想的标定效果，其中文献[4]提出的相机标定方法（以下简称Faugeras校准）因在参数求解和过渡环节等问题的处理上与文献[2-3]中提出的标定方法相比均存在显著优势而备受推崇，其待求参数求解环节少，计算公式简单，适用于图像变形校正与 C 形臂成像系统标定严格分离的手术导航系统[5-6]。闫士举[7]针对Faugeras校准过程中仍要经历中间环节的问题提出了改进的Faugeras校准方法，其直接求取校准参数，没有中间过渡环节，算法结构大大简化；但是该改进方法在参数求解过程中的约束条件使得求解过程还存在一定的繁琐之处。

由于基于C型臂的手术导航系统中的相机标定的最终目的是为了实现3D空间数据转换成2D图像数据，本文借鉴闫士举[7]针对Faugeras校准方法改进时所用到的忽略相机模型的想法，提出一种新的解决方案。该方案完全忽略相机模型，进一步简化过渡环节，使得求解过程变得简单，同时精度也能够得以保证。本研究还改进了校准靶，借助校准靶实现图像变形矫正，并提取矫正后的校准靶图像数据用于相机标定；在实现3D空间坐标向2D图像坐标的映射后搭建了导航实验平台，进行了相关实验，进一步验证了本文所提出的解决方法。

1校准靶的设计

校准靶是基于C形臂手术导航系统中的一个关键部件。根据功能要求，其上应带有按一定规则布置的金属网格或金属小球。手术前，先将校准靶固定在C型臂的影像增强器（X-ray Image Intensifier， XRII）端，获取若干幅图像，然后对小球在图像中投影进行识别并提取其几何数据。XRII图像变形校正及后续的C型臂成像系统标定都必须借助这些几何数据才能实现。本文研究中，自行设计制造了校准靶。

如图1所示：图（a）为自行设计的校准靶，侧面装有3个供定位跟踪仪定位使用的跟踪器（Tracker），上下两层有机玻璃上装有按一定规则排列的金属球，下层钢珠直径比上层金属球大，所拍摄的校准靶X线图像如图（b）所示。

2相机标定

相机标定是基于C形臂的手术导航系统实现所必须解决的关键技术之一，其本质为构建一个从空间3D立体患部到2D图像的投射模型，并求解3D空间坐标到2D图像坐标系的转换映射参数[8-9]，是手术实体可视化的必经环节。

3实验与分析

相机标定需要借助于校准靶在图像中的投影数据，故需先对校准靶在图像中的参数进行提取。由于所拍摄的校准靶图像存在一定的变形，所提取的数据不能直接用于相机标定，需要对图像先进行矫正。

3.1标志物投影数据提取

由于所拍摄的校准靶图像中目标与背景差别较大，所以本文研究采用自动取阈的方法从背景中分离标志物投影，并采用连通量分析（Connected Components，CC）的方法计算出小球投影的质心和面积。

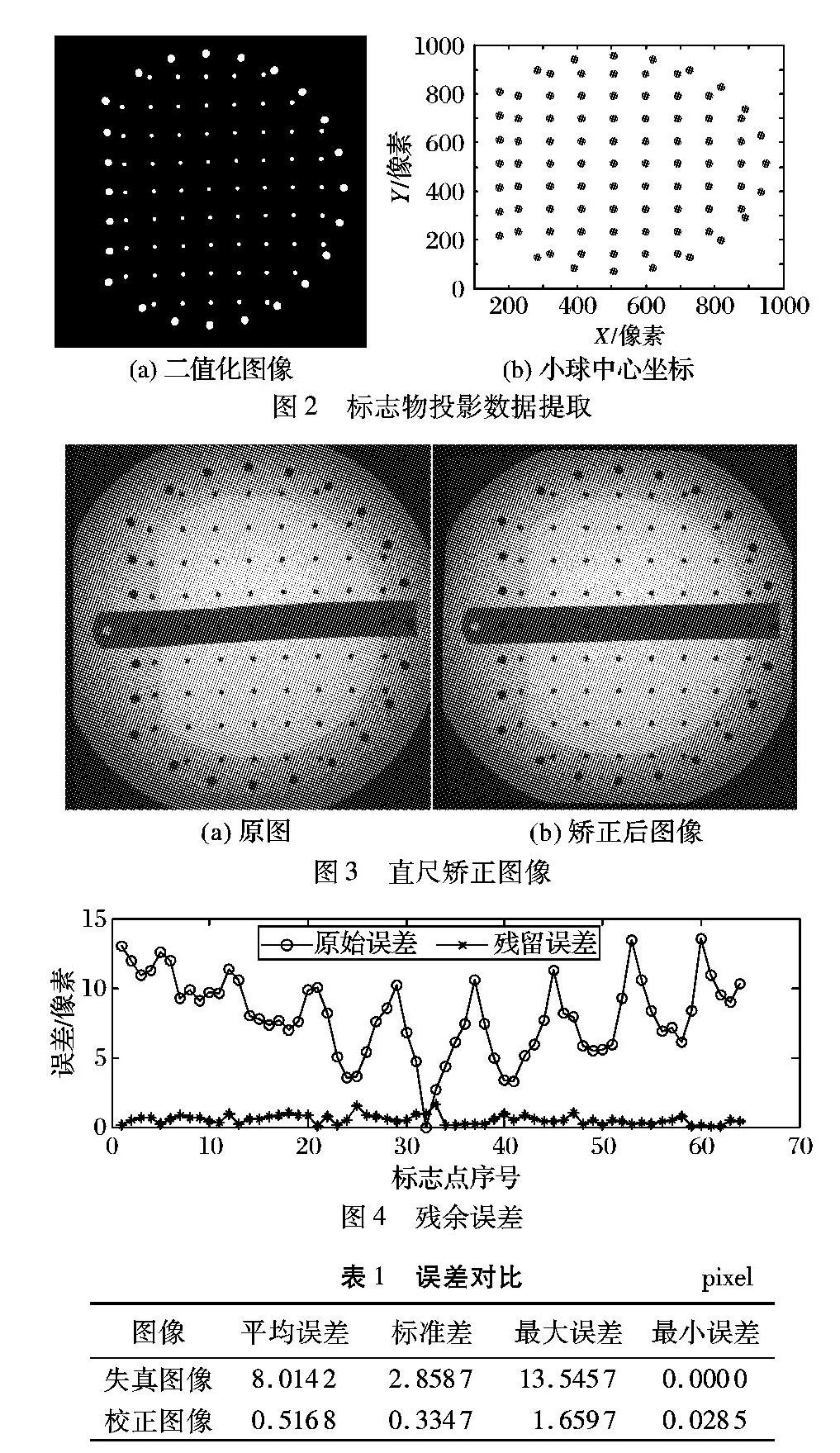
如图2所示：图（a）为经最大化类间分割法[10-11]分割后的XRII图像，白色圆形即为小球投影区域；图（b）为经连通量分析后获得的小球坐标数据。

3.2图像矫正

由于成像机制、外部环境及设备制造装配误差等方面的原因[12-13]，通过C型臂影像增强器获得的图像总是存在着变形失真，若直接提取标志物坐标面积数据用作图像矫正和相机标定则将影响最终的手术导航精度，故需对图像先进行矫正[14-17]。

本文研究采用全局多项式拟合失真变形[18-21]，向后插值获得矫正图像。图3为拍摄的直尺图片：图（a）中可以明显看到变形的存在，图（b）为矫正后的图像。图4可以看到误差明显降低，表1则显示畸变控制点相对于理想控制点的误差为8.0142像素，矫正后的残余误差为0.5168像素。

3.3相机标定

在校准靶上建立如图5所示坐标系，并根据校准靶设计参数得到钢珠三维坐标数据，如图6（a）所示。对矫正后的校准靶图像重新提取的钢珠的中心坐标，如图6（b）所示，选取上层板48个点和下层板14个点，将这些点的图像坐标和三维坐标数据按式（2）作拟合，并用最小二乘法求解得到3D到2D的映射参数。将剩余的26个点用作验证，如表2所示：

（X，Y，Z）表示校准靶坐标系下钢珠中心坐标；（u，v）表示理想图像中钢珠中心坐标；（u′，v′）表示（X，Y，Z）经式（2）变换后在图像中所映射的点的坐标，坐标残余误差均在0.002像素以下，精度较高。由于式（2）中的变换矩阵的求解只需要一步，并不存在Faugeras校准和闫士举[7]的改进方法中的限制条件，无需对求解过程中矩阵进行拆解，所以效率上有所提高。

3.4导航验证

为进一步验证本文方案的可行性，在实现上述关键技术的基础上搭建了如图7所示的基于C型臂的手术导航系统实验平台。利用搭建的平台拍摄校准靶图像，同时用Northern Digital Inc公司的Polaris光学定位跟踪系统记录校准靶位姿，将探针末端顶在校准靶上层模板安装的钢珠上（钢珠直径2mm），则在校准靶图像上显示白色点，如图8所示。

采集如图9（a）所示的测试装置（圆柱体上打有半径不同的圆孔）的正侧位X光图像，同时记录测试装置与校准靶位姿，并在自行开发的导航软件中计算位姿转换关系。将采集的图像矫正后调入导航界面（如图9（b））。

根据导航界面上提供的投影信息，调整探针对准（如图10（a）所示，左边是导航界面，粗线代表探针实体，细线代表探针轴线），沿着调整好的轴线方向成功将探针穿入（如图10（b）所示），同时能穿过其他孔。

4结语

针对基于C型臂的手术导航系统中相机标定过程中过渡环节过多、参数求解过程复杂等问题，本文提出了一种新的解决方案。该方案忽略了相机模型，在相机标定参数验证中体现出其高精度；并使用搭建的实验平台进行了探针取点及穿孔实验，验证了该方案的可行性。本文方案虽然解决了3D空间到2D图像的映射问题，但是因为完全忽略了相机模型，无法获取相机内外部参数，故其无法解决2D图像到3D空间的映射问题。若导航系统扩展到机器人辅助导航系统，上述问题则需结合反投射模型进行解决。下一步研究重点为借助反投射模型解决2D图像空间到3D空间的映射问题。

参考文献：

[1]郭乃铭，周跃.计算机辅助手术导航系统在脊柱外科手术中的应用进展[J].中国矫形外科杂志， 2013， 21（8）： 787-789. （GUO N M， ZHOU Y. The application progress of computer assisted surgery navigation system in spinal surgery [J]. Orthopedic Journal of China， 2013， 21（8）： 787-789.）

[2]GREMBAN K D， THORPE C E， KANADE T. Geometric camera calibration using systems of linear equations [C]// Proceedings of the 1988 IEEE International Conference on Robotics and Automation. Piscataway， NJ： IEEE， 1988： 562-567.

[3]TSAI R Y. A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses [J]. IEEE Journal of Robotics and Automation， 1987， 3（4）： 323-344.

[4]FAUGERAS O. Three-dimensional computer vision： a geometric viewpoint [M]. Cambridge， MA： MIT Press， 1993：247-289.

[5]BERTELSEN A， GARIN-MUGA A， ECHEVERRíA M， et al. Distortion correction and calibration of intra-operative spine X-ray images using a constrained DLT algorithm [J]. Computerized Medical Imaging and Graphics， 2014， 38（7）： 558-568.

[6]ZHU H， XU J， HE D， et al. Design and implementation of the moving workpiece sorting system based on LabVIEW [C]// CCDC 2014： Proceedings of the 26th Chinese Control and Decision Conference. Piscataway， NJ： IEEE， 2014： 5034-5038.

[7]闫士举. 基于C形臂手术导航关键技术研究及系统实现[D]. 上海交通大学， 2008： 95-99. （YAN S. Research on key technology of C-ARM based surgical navigation and development of application system [D]. Shanghai： Shanghai Jiao Tong University， 2008： 95-99.）

[8]MENG C. New method for geometric calibration and distortion correction of conventional C-arm [J]. Computers in Biology and Medicine， 2014： 52：49-56.

[9]周晓君. C形臂图像校正与手术定位技术研究[D].北京：北京邮电大学，2010：7-9. （ZHOU X. Study on image correction & location technique of C-ARM [D]. Beijing： Beijing University of Posts and Telecommunications， 2010： 7-9.）

[10]范朝冬，欧阳红林，肖乐意，等.基于空间截面投影的 Otsu 图像分割算法[J].通信学报， 2014， 35（5）： 70-78. （FAN C D， OUYANG H L， XIAO L Y， et al. Otsu thresholding method based on projection of cross section for image segmentation [J]. Journal on Communications， 2014， 35（5）： 70-78.）

[11]NG H F. Automatic thresholding for defect detection [J]. Pattern Recognition Letters， 2006， 27（14）： 1644-1649.

[12]GRONENSCHILD E. Correction for geometric image distortion in the x-ray imaging chain： local technique versus global technique [J]. Medical Physics， 1999， 26： 2602-2616.

[13]FANTOZZI S， CAPPELLO A， LEARDINI A. A global method based on thin-plate splines for correction of geometric distortion： an application to fluoroscopic images [J]. Med Phys. 2003， 30（2）： 124-131.

[14]李元金，舒华忠，罗立民，等.Delaunay三角网插值在 XRII图像扭曲校正中的应用[J].东南大学学报（英文版），2014（3）：306-310.

LI J Y， SHU H Z， LUO L M， et al. Application of the Delaunay triangulation interpolation in distortion XRII image [J]. Journal of Southeast University （English Edition）， 2014（3）： 306-310.

[15]邱文杰，陈坤斌，刘琼，等.基于移动最小二乘法的图像变形及GPU 实现[EB/OL].北京：中国科技论文在线 [2013-12-02]. http：//www.paper.edu.cn/releasepaper/content/201312-1. （QIU W J， CHEN K B， LIU Q， et al. Image deformation using MLS and implementation with GPU [EB/OL]. Beijing： Sciencepaper Online [2013-12-02]. http：//www.paper.edu.cn/releasepaper/content/201312-1.）

[16]LIAO G， HU Y， LI Z， et al. Human-computer interaction system based on binocular stereo vision [C]// CCC 2012： Proceedings of the 31st Chinese Control Conference. Piscataway， NJ： IEEE， 2012： 3640-3644.

[17]孙静坤，曾勇明，郁仁强，等.C型臂锥形束CT成像偏离正中心点对图像噪声及变形程度的影响[J].中国医学影像技术， 2014， 30（7）：1095-1099. （SUN J K， ZENG Y M， YU R Q， et al. Impact of offsetting center point on image noise and deformations in C-arm cone beam CT [J]. Chinese Journal of Medical Imaging Technology， 2014， 30（7）： 1095-1099.）

[18]王田苗，刘文勇，胡磊，等.基于多项式拟合的C臂投影全局校正法[J].高技术通讯，2007，17（9）：919-923. （WANG T M， LIU W Y， HU L， et al. Polynomial fitting-based global correction method for C-arm projection images [J]. Chinese High Technology Letters， 2007， 17（9）： 919-923.

[19]张军，孟偲.基于成像模型的C臂图像校正方法[EB/OL].北京：中国科技论文在线 [2012-11-14]. http：//www.paper.edu.cn/releasepaper/content/201211-232. （ZHANG J， MENG S. Distortion correction based on visual model for C-arm images [EB/OL]. Beijing： Sciencepaper Online [2012-11-14]. http：//www.paper.edu.cn/releasepaper/content/201211-232.）

[20]陈槐，钟强，李丹勋，等.多级网格迭代的图像变形算法在PIV中的应用[J].流体力学，2013，1（2）：34-39. （CHEN H， ZHONG Q， LI D X， et al. Iterative multigrid image deformation method for PIV[J]. International Journal of Fluid Dynamics， 2013， 1（2）： 34-39.）

[21]HERRMANN C. Method and apparatus for image correction of X-ray image information： U.S. Patent 20，150，316，663 [P]. 2015-11-05.