基于协方差矩阵降维稀疏表示的二维波达方向估计

李文杰　杨涛　梅艳莹

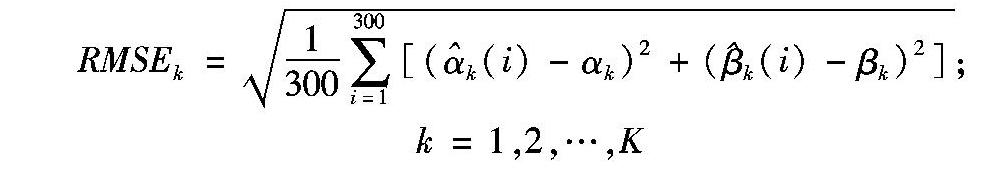
摘要：针对稀疏重构下二维波达方向（2D-DOA）估计存在计算量大的问题，提出一种基于协方差矩阵降维稀疏表示的二维波达方向估计方法。首先引入空间角构造流形矢量矩阵冗余字典，将方位角和俯仰角组合从二维空间映射到一维空间，降低了字典的长度和求解复杂度，并且能自动实现俯仰角和方位角配对；其次改进了样本协方差矩阵的稀疏表示模型，对该模型进行了降维处理；然后由协方差矩阵稀疏重构的残差约束特性得到约束残差项置信区间，避免采用正则化方法导致参数选取困难；最后通过凸优化包实现了二维波达方向的估计。仿真实验表明，待选取的协方差矩阵列数达到某个阈值（在只有两个入射信号情况下该值为3）时，可准确实现入射信号角的估计；当信噪比（SNR）较小（<5dB）时，该方法估计精度优于基于空间角的特征矢量算法；低快拍数（<100）下该方法估计精度略低于特征矢量法，但小间隔角度下估计精度与后者相当。

关键词：稀疏表示；二维波达方向估计；协方差矩阵；空间角；L型阵列

中图分类号：TN911.23

文献标志码：A

0引言

二维波达方向（Two-Dimensional Direction-Of-Arrival， 2D-DOA）估计作为信号处理领域的重要方向之一，在各个领域都有着广泛的应用，比如雷达、检测、通信等。随着技术的发展更是对波达方向估计提出了高精度、高分辨率、解相干等要求。阵列信号的空间谱非连续性，仅在相应的空间方位存在非零值，产生了稀疏表示求解波达方向估计思想。在一维波达方向估计（One-Dimensional Direction-Of-Arrival， 1D-DOA）方面，许多学者已经对稀疏算法进行了大量的研究[1-3]。

实际中，二维参量比一维参量更加具有实用价值和研究意义。以多重信号分类（MUltiple SIgnal Classification， MUSIC）[4]、旋转不变子空间（Estimation of Signal Parameters via Rotational Invariance Techniques， ESPRIT）[5]算法为代表的子空间类估计方法通常需要较高的信噪比（Signal-to-Noise Ratio， SNR）门限和较多的采样快拍，并且需要事先已知信号的信源数。此外，MUSIC算法对相干信号需进行去相干处理，容易造成阵列孔径损失问题，限制了其应用。Malioutov等[6]提出了l1范数奇异值分解（l1-norm Singular Value Decomposition， l1-SVD）方法，利用l1范数约束求解稀疏目标估计值。但此方法需要事先知道入射信号信源数，当信源数超出估计值时，带来性能严重下降问题。当进行2D-DOA估计时，l1-SVD算法计算量会变得非常庞大。张妍君[7]提出一种利用l1范数项和Capon谱约束解决参数选择问题的二维稀疏估计算法，避免了正则化参数的选取不当而降低算法性能。但由于引入Capon谱，不适宜处理相干信号。李鹏飞等[8]提出空间角稀疏求解DOA估计方法，利用空间角构造冗余字典，降低了计算难度，但没有避免正则化参数选取，对算法性能有较大影响。

对此，本文提出利用协方差部分信息稀疏求解2D-DOA估计的方法，首先依据阵列的方向矢量作为原子给出阵列信号的稀疏模型。对阵列输出协方差矩阵列数降维处理，利用阵列输出协方差矩阵某几列进行波达方向估计，且通过引用变换矩阵避免了正则化参数的选取。同时利用空间角概念，降低了计算的复杂度。

1阵列信号模型

假定两个均匀线性正交阵列，组成L型阵列结构，共由2M-1个阵元组成，具体结构如图1，阵元间距d=dx=dz=0.5λ，λ为信号波长；俯仰角θk定义为信号来波方向与坐标系z轴正向的夹角，角度范围为：0<θk<180°；方位角φk为信号来波方向在x-y平面投影与坐标系x轴夹角，同样角度范围为：0<φk<180°。

3基于协方差矩阵的稀疏估计方法

3.1阵列接收信号处理

文献[9-10]提出根据协方差矩阵估计波达方向方法，但是必须要知道噪声功率的限制。本文方法以子阵Z的接收信号rz（t）为例进行说明，对子阵X也类似。根据前面设定的信号与噪声之间不相关性质，则根据式（9），Z子阵列输出协方差矩阵可表示为：

3.2方位角和俯仰角配对

大多数情况下，用分维方法进行方位角和俯仰角估计的时候，比较困难之处在于方位角和俯仰角的配对问题。利用稀疏分解可得到信号幅值，进而可以根据信号幅值得到信号的方位信息，可实现俯仰角和方位角配对问题。

在式（16）中，Bz和Bx中非零元素的位置代表了入射信号对应的空间角的值，非零元素的值代表了入射信号对应的幅度信息，据此可同时求解空间角α和β的值，实现自动配对，经过式（6）就可以反推得θ和φ。

3.3阵列输出协方差矩阵列数优化

通过第2章可知使用空间角可以降低计算复杂度，将2D-DOA估计问题转化为1D-DOA估计问题。通过3.2节可知道空间角α和β与方位角俯仰角θ和φ之间存在对应关系，因此可以用空间角α和β来进行2D-DOA估计计算。

协方差矩阵列数的增加会造成算法的计算复杂度增大，为了选取最优的阵列协方差矩阵列数，这里通过逐步增加列数的方法进行搜索。假定入射信号个数在短时间内保持不变，则其输出协方差矩阵的秩也保持不变，在这段时间内可选取相同的输出协方差矩阵列数，这样可明显降低计算量。假定子阵元数目M=8，信源数为2个，信源1的俯仰角和方位角设为α1=35°、 β1=30°，信源2的俯仰角和方位角设为α2=60°、 β2=70°，信号和噪声不相关。信噪比为20dB，快拍数设为200，独立实验的次数为300，本文采用每个信源俯仰角和方位角估计误差平方和求得均方根误差（Root Mean Squared Error，RMSE），定义如下：

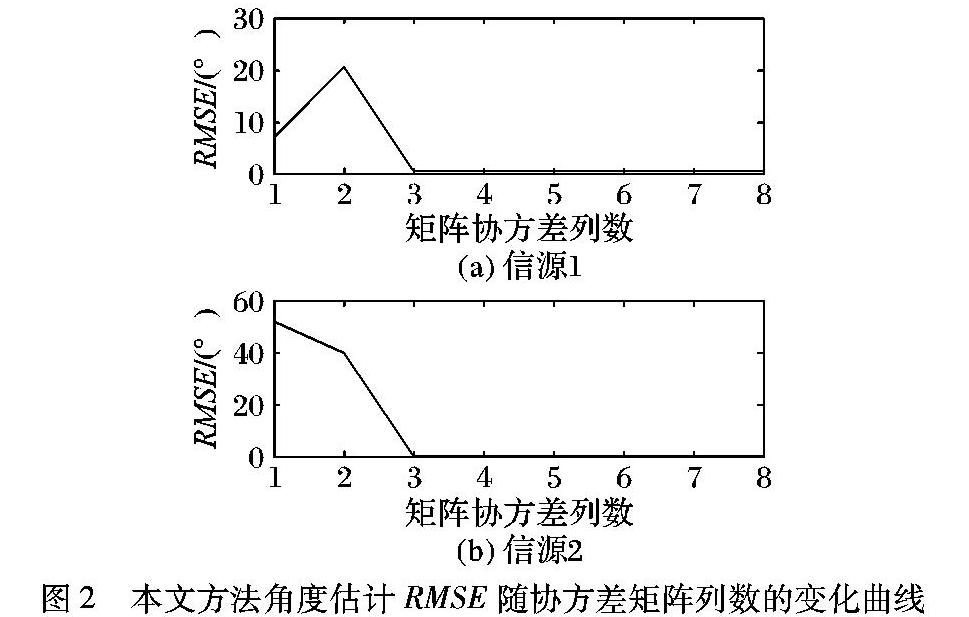
文献[11]中第4章中提到：基于协方差矩阵的稀疏表示波达方向估计方法实际上是利用协方差矩阵列向量的联合稀疏特性来进行的，实际中为降低计算复杂度，只需对某几列进行联合稀疏求解就可以获得很好的性能，规定协方差矩阵列数Q≤M。在假定2个远场入射信号情况下，为选出计算复杂度最小且不影响DOA估计性能的最优列数，从最小列数（1）到最大列数（子阵元数M），取单个信源均方根误差，图2显示了两信源角度估计的均方根误差RMSE随协方差列数变化的关系。

从图2可以看出，当协方差矩阵列数增加到3列时，角度估计的均方根误差趋于0，满足条件，此时可以准确地估计出入射角的信息。当入射信号的个数发生变化时或者部分阵元失效时，可定时采用上述方法搜索最优的协方差矩阵列数，从而减少计算量。

从减少计算量与平衡算法的性能角度出发，本文协方差矩阵列数选择3列，当然为了使结果更加精确，可根据需要适当增加阵列数目。

3.4计算复杂度分析

本文算法的计算量主要在于利用内点法对凸优化包形式求解，算法复杂度为O（N3），而同类稀疏表示算法中，文献[8，12]的方法（下文简称特征矢量法）也主要集中于对凸优化的求解，算法复杂度也为O（N3）。子空间类MUSIC算法复杂度为O（M3），通常情况下NM，MUSIC算法具有较低的复杂度，本文算法与特征矢量法相当。

4仿真实验与分析

本章主要进行各种仿真验证，文献[8]中已经对比了eigenvector算法与MUSIC算法，结果显示eigenvector算法的性能远优于MUSIC算法，这里不再重复比较，主要将本文方法与特征矢量法作比较。仿真的基本条件与3.3节中相同。子阵元数目M=8，信源数为2个，信源1的俯仰角和方位角设为α1=35°、 β1=30°，信源2的俯仰角和方位角设为α2=60°、 β2=70°，信号和噪声不相关，独立实验的次数为300。

公式重复定义，而且下标k表示什么？

均方根误差定义如下：

，K

实验1比较信噪比与估计精度关系。

本实验比较两种方法估计精度与信噪比关系。基本条件同上，快拍数设为200，SNR在-10dB到20dB范围内变化。图3显示两信源的角度估计变化情况。从图3中可以看出，当SNR从-10dB增加到20dB过程中，本文方法估计精度变化较小，在信噪比较低时，估计精度高于特征矢量法，信噪比较大时，二者估计精度相当。

实验2比较快拍数与估计精度关系。

本实验比较两种方法估计精度与快拍数关系。基本条件同上，信噪比设为15dB，快拍数在2到600范围内取值。图4显示了快拍数从2到600的过程中两信源角度估计变化情况。从图4可以看出在快拍数从2增加到600过程中，本文方法在快拍数很小情况下估计精度略低于特征矢量法，其他情况下两种方法估计精度相同。

实验3比较角度间隔与估计精度关系。

本实验比较两种方法在角度间隔下的分辨能力。假定两信源互不相关，快拍数取为200，信噪比取为15dB。首先假定信源1和2的方位角不变，假设为30°，令α1=35°+δ，β1=30°，α2=55°+δ，β2=30°，δ从1变到5，看看估计算法的超分辨能力；其次假定信源1和2的俯仰角不变，假设为35°，令α1=35°，β1=30°+δ，α2=35°，β2=40°+δ，δ从1变到5，看看估计算法的超分辨能力。图5显示了在信源1和2的方

位角β1和β2不变时，δ从1变化到5过程中两信源估计精度变化情况。从图5中可以看出在俯仰角α间距增大过程中，估计精度略有下降，信源1和信源2的均方根误差RMSE曲线完全重合，说明两种方法的分辨能力相同。图6显示了在信源1和2的俯仰角α1和α2不变时，δ从1变化到5过程中两信源估计精度变化情况。从图6中可以看出随方位角β间距增大过程中，信源1在两种方法下均方根误差曲线重合，信源2在两种方法下均方根误差RMSE曲线也重合，估计精度都略有下降，说明两种方法的分辨能力也相同。综合上述两种情况下的分析，本文方法与特征矢量法分辨能力相同。

实验4运算时间分析。

比较本文算法、特征矢量方法及去相干2D-MUSIC方法运行一次所需的时间，实验在配置相同的计算机上运行，笔记本型号为宏基GT520M系列，CPU为Intel 酷睿i3 380M、内存为2GB、操作系统为Windows 7，得到运算时间如表1所示。

由表1可以看出，MUSIC算法运行一次所需时间最少，表明子空间算法复杂度小于稀疏重构算法。本文算法运行时间略低于特征矢量法，与3.4节中对算法复杂度的分析相符。

5结语

本文针对2D-DOA估计存在计算量大、无法实现角度自动匹配的问题，引入协方差矩阵稀疏表示模型和空间角的概念，构建一种新的2D-DOA估计方法，能自动实现俯仰角与方位角的匹配。该方法与可实现角度自动配对的稀疏类2D-DOA方法（如特征矢量法）相比，不需选取正则化参数，对信噪比和快拍数要求低，小间隔角度下估计精度稳定。

参考文献：

[1]WU X， ZHU W-P， YAN J. Direction of arrival estimation for off-grid signals based on sparse Bayesian learning [J]. IEEE Sensors Journal， 2015， 16（7）： 2004-2016.

[2]TIAN Y， SUN X， ZHAO S. Sparse-reconstruction-based direction of arrival， polarisation and power estimation using a cross-dipole array [J]. IET Radar， Sonar & Navigation， 2015， 9（6）： 727-731.

[3]LIU Z-M， HUANG Z-T， ZHOU Y-Y. An efficient maximum likelihood method for direction-of-arrival estimation via sparse Bayesian learning [J]. IEEE Transactions on Wireless Communications， 2012， 11（10）： 1-11.

[4]GAO F， NALLANATHAN A， WANG Y. Improved MUSIC under the coexistence of both circular and noncircular sources [J]. IEEE Transactions on Signal Processing， 2008， 56（7）： 3033-3038.

[5]JIAN C， WANG S， LIN L. Two-dimensional DOA estimation of coherent signals based on 2D unitary ESPRINT method [C]// Proceedings of the 8th International Conference on Signal Processing. Piscataway， NJ： IEEE， 2006： 16-20.

[6]

MALIOUTOV D， CETIN M， WILLSKY A S. A sparse signal reconstruction perspective for source localization with sensor arrays [J]. IEEE Transactions on Signal Processing， 2005， 53（8）： 3010-3022.

[7]张妍君.基于稀疏重构的信源定位算法研究[D].长春：吉林大学，2014： 37-46. （ZHANG Y J. Research on algorithm of source localization based on sparse recovery[D]. Changchun： Jilin University， 2014： 37-46.）

[8]李鹏飞，张旻，钟子发.基于空间角稀疏表示的二维DOA估计[J].电子与信息学报，2011，33（10）：2402-2406. （LI P F， ZHANG M， ZHEN Z F. Two-dimensional DOA estimation based on sparse representation of space angle [J]. Journal of Electronics and Information Technology， 2011， 33（10）： 2402-2406.）

[9]YIN J， CHEN T. Direction-of-Arrival estimation using a sparse representation of array covariance vector [J]. IEEE Transactions on Signal Processing， 2011， 59（9）： 4489-4493.

[10]HE Z Q， LIU Q H， JIN L N， et al. Low complexity method for DOA estimation using array covariance matrix sparse representation [J]. Electronics Letters， 2013， 49（3）： 228-230.

[11]解虎，冯大政，袁明冬.一种采用协方差矩阵稀疏表示的DOA估计方法[J].西安电子科技大学学报，2015，42（1）：36-41. （JIE H， FENG D Z， YUAN M D. DOA estimation method by utilizing sparse representation of the covariance matrix [J]. Journal of Xidian University， 2015， 42（1）： 36-41.）

[12]崔琛，王粒宾.利用空域稀疏性的L型阵下二维波达方向估计[J].电路与系统学报，2013，18（1）：297-303. （CUI C， WANG L B. Two-dimensional DOA estimation of L array using spatial sparsity [J]. Journal of Circuits and Systems， 2013， 18（1）： 297-303.）