地震信号随机噪声压制的双树复小波域双变量方法
2016-09-29汪金菊袁力刘婉如徐小红
汪金菊,袁力,刘婉如,徐小红
合肥工业大学数学学院,合肥 230009
地震信号随机噪声压制的双树复小波域双变量方法
汪金菊,袁力,刘婉如,徐小红
合肥工业大学数学学院,合肥230009
有效地压制地震信号中的噪声是地震信号解释和后续处理的重要环节之一.本文建立两种双树复小波域双变量模型对地震信号中的随机噪声进行压制.地震信号经双树复小波变换后,同一方向实部与虚部系数、实部(或虚部)系数与对应的模之间存在较强的相关性.鉴于此,对同一方向实部与虚部小波系数建立双变量模型,从含噪地震信号小波系数中估计原始信号的小波系数,再基于双树复小波逆变换重构得到降噪后的地震信号.进一步对同一方向实部(或虚部)系数与对应的模建立双变量模型,得到地震信号随机噪声压制的第二种双树复小波域双变量方法.最后对合成地震记录和实际地震资料中的随机噪声进行压制的实验结果证实本文两种方法都能够有效地压制地震信号中的随机噪声.
双树复小波变换;随机噪声;双变量模型;小波系数
1 引言
地震信号降噪的目的在于去除各种干扰,提高信噪比的同时较好地保留有效信号.随机噪声衰减是地震信号处理中的一个重要环节,对噪声的压制效果直接影响后续处理.为了提高信噪比,人们根据信号与噪声的特征差异,设计出各种降噪方法.以傅氏变换为基础的频率域滤波方法是地震资料处理中的经典方法,该方法根据有效波和干扰波在频带上的差异来压制干扰波突出有效波.该方法的不足在于信号的降噪效果依赖于信号频带和噪声频带分离的程度.若混入噪声的频带和信号频带有重叠时,则降噪效果不是十分理想.在此基础上,基于傅氏变换的f-x域预测地震信号降噪技术被提出,该技术可有效地压制随机噪声,但不能对非平稳地震信号进行很好的处理.
小波是一种具有多分辨率和时频局域性的分析工具,可将信号的特征表现在不同分辨层次上,信号的局部特征可以通过处理变换系数而改变,因而被广泛应用于信号降噪.一些学者利用小波变换这一时频分析工具解决非稳态问题,相继提出了二进小波变换方法的地震信号分时分频去噪(章珂等,1996)、小波包变换和f-x域预测相结合的降噪算法(宗涛等,1998)、基于小波域贝叶斯方法(张波等,1999)和最小二乘降噪算法(王振国等,2002).这类降噪方法首先将地震信号进行多尺度分解得到高低频子带系数,然后对包含随机噪声的子带系数进行处理,以达到降噪目的.它们在一定程度上提高了降噪效果,但未考虑小波域统计模型.基于拉普拉斯先验分布的软阈值法(Berkner and Wells,2002)开创性地分析了小波系数的统计特征.该降噪算法将拉普拉斯分布作为单个小波分解系数的统计分布,通过最大后验概率估计得到软阈值函数.以单变量概率密度函数作为先验分布求解阈值的单变量模型算法如软阈值法,由于只考虑子带内单个小波系数的统计特征,没有考虑子带间小波系数的相关性,虽然实现简单,但去噪效果不理想.SURE-LET算法(Luisier et al.,2007)的先验模型在尺度内较好地模拟小波系数的概率分布,但忽略了小波系数尺度间的相关性,且其先验统计模型相对简单,不够准确.基于贝叶斯估计的小波域双变量法(Sendur and Selesnick,2002)利用相邻尺度间小波系数的相关性,取得较好的降噪效果.随后此方法被应用于地震信号降噪(刘鑫等,2006),实验表明该方法具有良好的降噪性能.殷明等(2014)提出非下采样双树复小波域的双变量模型去噪算法,把双变量统计模型引入到非下采样双树复小波变换同一方向实部和虚部小波系数中,较为有效地去除图像中的随机噪声.
Kingsbury(1998)提出了双树复小波变换(Dual-tree Complex Wavelet Transform,DTCWT),对传统小波进行了增强,使其具有近似平移不变、多方向选择和低冗余的优良特性,因而被广泛应用于信号降噪、特征提取和分析等领域(Kingsbury,2001).由于地震信号具有明显的多尺度性,相邻道共深度点有效信号有较强相关性,利用双树复小波变换能较好地检测与表示地震信号的线状变化特征(如弯曲的同相轴等).双树复小波变换的提出解决了二维可分离小波不能很好地表示信号细节特征和方向选择少的不足,且系数的模具有旋转不变性.这些优点使它能更好地表示地震信号的高维奇异特征.
鉴于此,本文分析并验证了地震信号的双树复小波变换系数中同一方向实部与虚部小波系数之间,以及实部(或虚部)系数与对应的模之间具有较强的相关性.从而对同一方向实部与虚部系数,以及实部(或虚部)系数与对应的模分别建立双变量模型.以此从含噪地震信号小波系数中估计恢复原信号的小波系数,得到两种地震信号随机噪声压制的双树复小波域双变量方法.通过理论合成记录仿真实验和实际地震资料处理结果证实本文两种方法都能够有效地压制地震信号中的随机噪声.
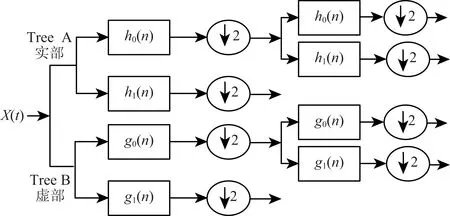
图1 一维双树复小波分解变换示意图Fig.1 1D dual-tree complex wavelet transform
2 双树复小波变换
双树复小波分解变换包含两个平行的分解树,需要用到两个独立的实小波来分别计算实部与虚部系数.实际中采用双树算法来实现分解变换.
图1展示了一维信号的双树复小波分解变换,其中h0(n)和h1(n)分别是树A分解过程的低通和高通滤波器,它产生实部的低频和高频小波系数;g0(n)和g1(n)分别是树B分解过程的低通和高通滤波器,它产生虚部的低频和高频小波系数;↓2表示下采样操作.
双树复小波所采用的实部滤波器组函数ψh(t)与虚部滤波器组函数ψg(t)构成一个复小波,即
(1)
双树复小波变换的优良性能来源于ψC(t)的解析性,为使ψC(t)满足解析性,则需要ψh(t)与ψg(t)构成一组希尔伯特变换对,即
(2)
使两个正交小波函数组成希尔伯特变换对的充要条件是:两低通滤波器满足半采样延迟条件(Coifman and Donoho,1995).则对正交小波基,有
(3)
(4)
(5)
式(5)与式(2)等价,称式(5)为半帧移条件.由于半帧移相当于在每个尺度对低通信号的采样提高到原来的2倍,这就极大地避免了由于二元下抽样导致的走样现象产生.双树结构和特殊滤波器的选择使变换具有近似平移不变性和频率无偏性.
二维双树复小波变换可通过一维双树复小波的张量积得到,分解时相当于对行和列分别进行一维双树复小波变换.因为双树复小波变换是冗余的,对于一维信号,产生2∶1的冗余度,而对于n维的信号,将产生2n∶1的冗余度.二维双树复小波变换过程中,各尺度生成2个低频子带和方向分别为±15°、±45°和±75°的6个不同高频子带,且每个方向子带有实部与虚部两个部分.对上一尺度的低频子带再进行分解操作可达到多尺度分解的目的,得到不同尺度不同方向的小波分解系数.
双树复小波变换后同一尺度内的各子带维数相同,同一位置的小波系数在同一尺度内的各子带位置固定,这样有利于分析同一位置小波系数间的统计特性.用合适的分布拟合小波系数分布,并通过分析系数间的相关性特征,建立合适的统计模型,可提高信号降噪方法的能力(Hill et al.,2012).
3 双树复小波子带系数相关性分析
基于小波域的降噪算法中,如何利用小波系数的统计分布特征一直是地震信号降噪算法领域的一个研究热点.小波系数具有零均值和重尾性,它的边缘分布近似服从拉普拉斯分布、广义高斯分布或混合高斯分布等非高斯统计分布.但是仅仅利用这些边缘分布特征描述小波系数特征是不够准确的,因为这类边缘统计分布特征忽略了小波系数之间的相关性.因此,如何建立较为准确的数学模型来描述系数之间的相关关系,从而提高降噪效果是研究的难点(Yin and Liu,2012).
小波系数具有传递和聚集的特性,即幅值较大系数的邻域系数幅值也较大,且在其他尺度同一位置系数的幅值也较大(Shi and Selesnick,2007).Sendur和Selesnick(2002)提出的双变量阈值降噪法考虑了小波系数间的相关性,把小波系数的统计特征引入模型以提高降噪效果.由于双树复小波的实部和虚部滤波器构成希尔伯特变换对,因此信号经双树复小波变换后,同一方向实部与虚部系数具有相关性.另外双树复小波系数的模具有旋转不变性,为了将这一性质应用于双变量模型,本文还考虑了实部(或虚部)系数与模的相关关系.为了衡量实部与虚部系数、实部(或虚部)系数和模之间的相关性,本文采用互信息(Liu and Moulin,2001)作为度量标准.对于两个变量z1和z2之间的互信息I(z1;z2)可表示为
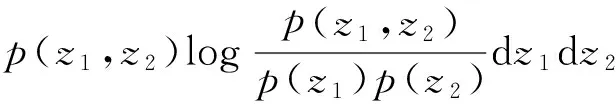
(6)
其中p(z1)和p(z2)为z1和z2的概率密度函数,p(z1,z2)为z1和z2的联合概率密度函数.并利用Peng等(2005)所述方法计算互信息值I(z1;z2).互信息值越大,表示变量之间的相关性越强.为了便于实验,对采样点数为512,道数为512的4个合成地震记录进行2层双树复小波变换,对分解得到的子带系数进行互信息计算,分别计算父子系数、相邻系数、实部与虚部系数、实部(或虚部)系数与模之间的互信息值,列出部分子带间互信息值如下表1所示.
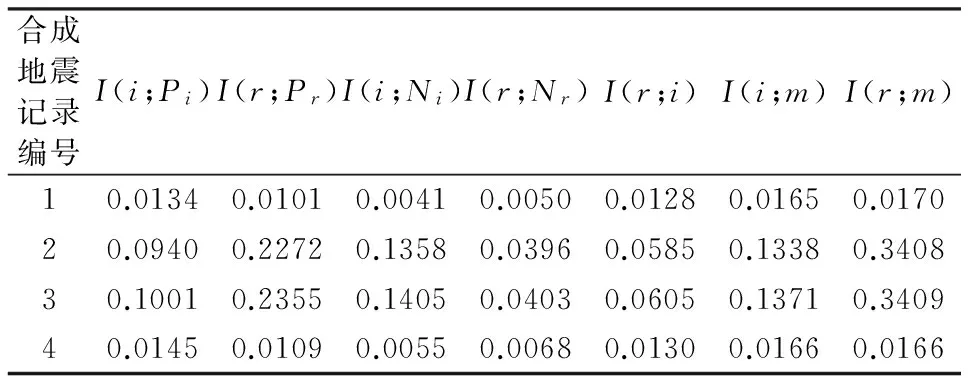
表1 双树复小波变换子带系数的互信息
在表1中r、Pr和Nr分别表示实部系数、其对应的父系数和邻域系数;i、Pi和Ni分别表示与r同一方向虚部系数、其对应的父系数和邻域系数,m是实部与虚部系数对应的模,其中
(7)
当式(6)中的变量z1和z2分别为r、Pr、Nr、i、Pi、Ni、m中的两者时,I(z1;z2)表示这两个子带系数之间的互信息值.
从表1中看出,同一方向的实部与虚部系数、实部(或虚部)系数与模存在着较强的相关性.相邻尺度间系数即某一子带系数与其父系数子带大小不同,系数位置不固定,子带系数与其邻域系数虽子带大小相同,在互信息度量时,考虑了取其邻域的平均值,这些都影响了相关性的计算与运用.由双树复小波分解变换特点知,同一方向的实部与虚部系数、实部(或虚部)系数与模子带大小一致,系数位置固定,便于度量与应用.所以本文考虑运用实部与虚部系数、实部(或虚部)系数与模之间的相关性建立统计模型.
4 双树复小波域双变量模型
4.1实部与虚部系数的双变量模型

(8)
在给定含噪地震信号s的前提下,地震信号降噪的目的是根据一定的准则尽可能地恢复原始地震信号x.在双树复小波域中,含噪模型可以表示为
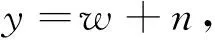
(9)
其中,y为含噪小波系数,w为原始地震信号小波系数,n为噪声的小波系数.
考虑同一方向实部与虚部小波系数之间相关性,构造双变量模型.假设
(10)
其中y1和y2是含噪地震信号同一方向的实部和虚部小波系数,w1和w2是对应的原信号小波系数的实部和虚部,n1和n2为对应的噪声小波系数的实部和虚部.式(10)可以改写成向量的形式:

(11)
其中w=(w1,w2)T,y=(y1,y2)T,n=(n1,n2)T.
(12)
利用条件概率公式进行推导,式(12)可变为
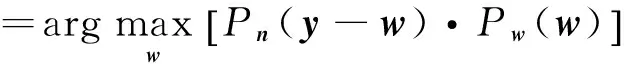
(13)
为了计算方便,进行对数变换后式(13)等价于
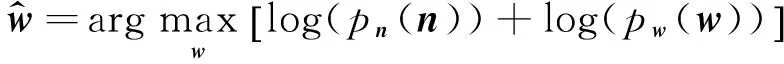
(14)
假设噪声是独立同分布的高斯白噪声,这种噪声在经过双树复小波变换后仍服从高斯分布,即概率密度函数为
(15)
设原地震信号同一方向实部与虚部小波系数的双变量联合概率密度函数为
(16)
其中a是待定参数,σ2表示被估计信号小波系数的方差.
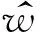
(17)
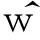
(18)
4.2实部(或虚部)系数与模的双变量模型
基于文中第3节的相关性分析,实部(或虚部)系数与模之间具有较强的相关性.故将实部与虚部系数的双变量模型推广建立实部(或虚部)系数与对应模的双变量模型.假设:
(19)
假设原地震信号实部系数与模的双变量联合概率密度函数为
(20)
其中t是待定参数,σ2表示被估计信号小波系数的方差.
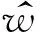
(21)
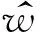
(22)
5 双树复小波域双变量模型降噪方法
5.1参数估计
(23)
其中yi为高频子带系数.
(24)
(25)
其中N是邻域U的大小.利用式(24)和(25)可得σ2的估计值:
(26)
对地震数据降噪效果的评价可以选用信噪比(SNR)进行定量评价.SNR的公式定义如下:
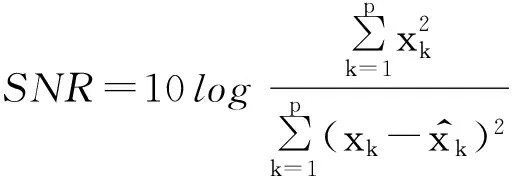
(27)
为了研究参数a和t对降噪效果的影响,本文选取5个合成地震信号数据,并对其分别加入标准差为10、20、30的高斯白噪声进行实验.下面的图2展示了当参数a的取值范围为[0,5]时采用双树复小波域实部与虚部系数组成的双变量模型降噪方法对SNR的影响,以及参数t取值范围为[0,8]时实部(或虚部)系数与模组成的双变量模型降噪方法对SNR的影响.图2(a、b、c)中的5条曲线分别表示了5个不同地震数据降噪后SNR随着参数a取值变化而变化.观察得知在一定范围内,SNR值先是随着参数a取值的增大而逐渐上升,在[1.5,3]间达到最大,即在此处取得较好的降噪效果.当参数a取值继续增大时SNR平缓地减小,对于加入了不同大小方差噪声的合成地震数据皆有这一特征.图2(d、e、f)中的5条曲线分别表示了5个不同地震数据降噪后SNR随着参数t取值变化而变化,得到参数t最优取值范围为[2,4].因此本文取参数a经验值为3,参数t经验值为4.

图2 参数a及t对SNR的影响(a)、(b)和(c)噪声标准差分别为10,20,30时参数a对SNR的影响;(d)、(e)和(f)噪声标准差分别为10,20,30时参数t对SNR的影响.Fig.2 The influence of parameter a and t on SNR(a)、(b)and (c)The influence of parameter a on SNR with standard deviation equals to 10,20,30;(d)、(e)and (f)The influence of parameter t on SNR with standard deviation equals to 10,20,30.
5.2降噪方法的算法步骤
本文中的双树复小波域实部与虚部系数组成的双变量降噪方法的算法步骤如下:
步骤1:对含噪地震信号进行双树复小波分解变换,得到每一尺度2个低频子带和6个不同方向的高频子带,且每个子带有实部与虚部两个部分;
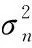
步骤3:低频系数保持不变,而对高频同一方向实部与虚部系数,运用式(17),(18)估计出不含噪地震信号的实部与虚部高频小波系数.从而得到各尺度各方向的小波分解系数的估计值;
步骤4:对小波分解系数的估计值进行双树复小波逆变换重构得到降噪后的地震信号.
本文提出的双树复小波域实部(或虚部)系数与模组成的双变量降噪方法的算法步骤与上面步骤类似,不同之处在于步骤3利用式(21)和(22)估计出不含噪地震信号高频小波系数的实部与虚部.
6 仿真实验与分析
为了验证本文降噪方法压制地震信号随机噪声的有效性,利用MATLAB2014a进行算法的仿真实验.首先生成合成地震信号,并对其加入标准差为30的高斯白噪声,对添加噪声后的地震信号进行一层二维双树复小波分解变换,所得到的小波系数如图3所示.
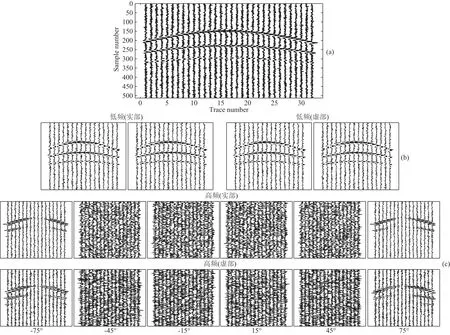
图3 含噪合成地震信号及其一层双树复小波分解系数(a)含噪地震信号;(b)低频系数;(c)6个角度方向的高频系数.Fig.3 The noisy synthetic seismic signal and the one layer dual tree complex wavelet transform coefficients(a)The noisy seismic signal;(b)The low frequency coefficients;(c)The high frequency coefficients of the six angles.
图3显示了含噪合成地震信号经过一层双树复小波分解后的低频与高频小波系数.观察图3(b,c)发现随机噪声主要集中于高频系数中.直观上可看出同一方向实部与虚部系数有较为明显的相关性.因此本文方法只对高频系数进行处理,而保持低频系数不变.最后对压制噪声后的小波系数进行双树复小波逆变换,得到压制噪声后的地震信号.
为了进一步说明本文方法的有效性,对合成地震数据加入不同大小方差的高斯白噪声,将本文方法与基于父子系数的离散小波域双变量阈值(DWT Bishrink)降噪方法(Abdelnour and Selesnick,2001)和基于父子系数的双树复小波域双变量阈值(DTCWT Bishrink)降噪方法(Sendur and Selesnick,2002,刘鑫等,2006)进行比较,其中各小波分解层数均为4层.本文中双树复小波域实部与虚部系数组成的双变量降噪方法记为方法1,双树复小波域实部(或虚部)系数与模组成的双变量降噪方法记为方法2.以SNR与均方误差(MSE)作为评价标准,MSE的公式定义如下:
(28)
从表2中可以看出,本文两种方法得到的SNR值明显大于其他两种方法得到的值,MSE值明显小于其他两种方法得到的数值.因此本文两种方法的降噪效果更好,且多数情况下方法2的结果稍优于方法1的结果.
为了能够更好地体现实验效果,在仿真实验中取加噪地震信号其中的某一道地震数据进行观察.选择降噪效果较好的DTCWT Bishrink方法与本文方法2进行降噪效果比较.表2中降噪前信噪比为-4.50dB地震信号的第11道地震数据的降噪结果局部放大比对图及对应的振幅谱比较图如图4所示.
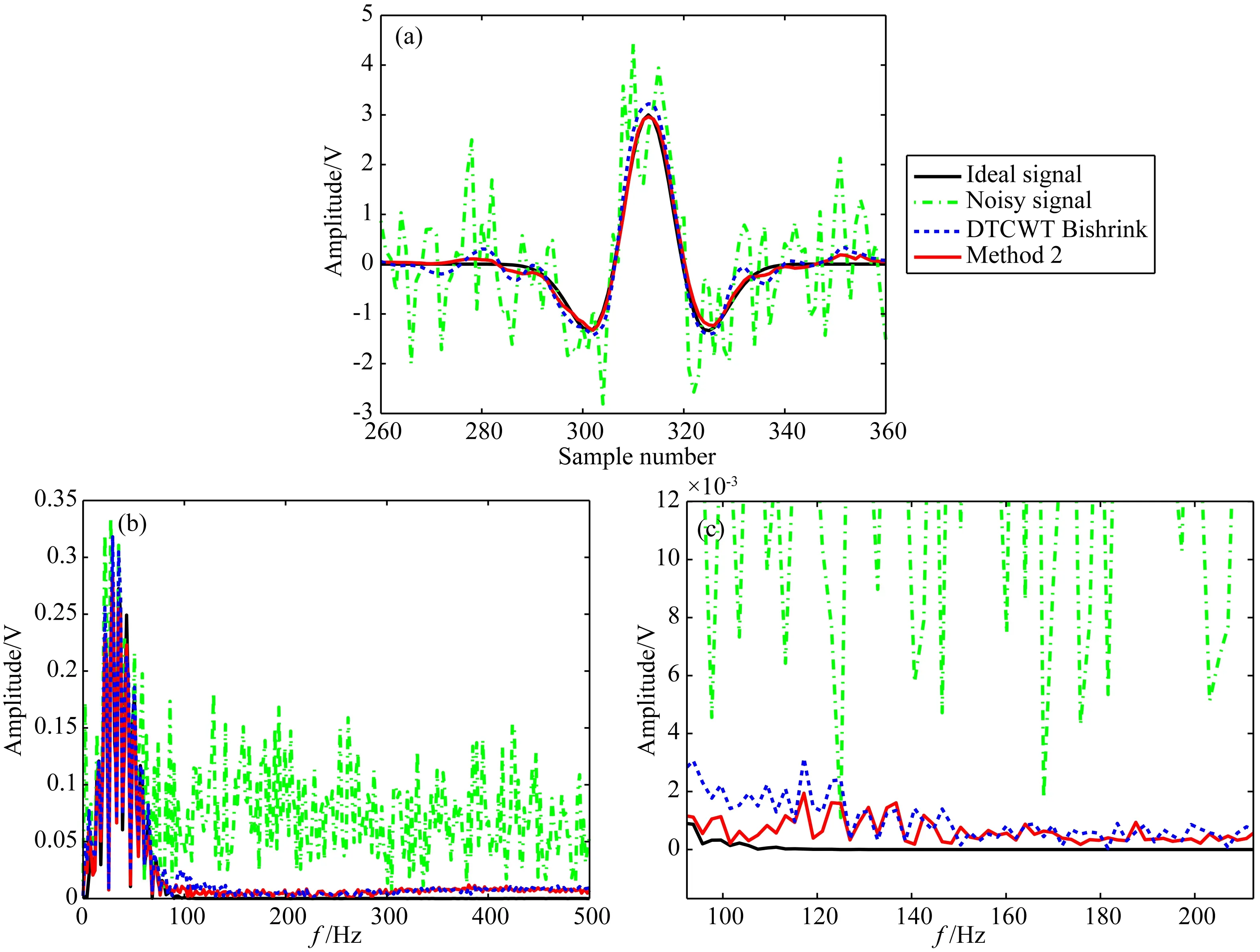
图4 单道地震信号降噪结果及对应的振幅谱(a)原始地震信号、加噪地震信号、DTCWT Bishrink方法和方法2降噪结果局部放大比较图;(b)地震信号及其降噪后信号对应的振幅谱;(c)振幅谱的局部放大图.Fig.4 The denoised results of the single channel seismic signal and their corresponding amplitude spectrums(a)The local enlarged figure of the ideal seismic signal、the noisy seismic signal、the denoised seismic signals via the DTCWT Bishrink and the method 2;(b)The amplitude spectrums of the seismic signal and the denoised seismic signals via the DTCWT Bishrink and the method 2;(c)The local enlarged figure of the amplitude spectrums.

降噪前DWTBishrinkDTCWTBishrink方法1方法2SNRSNRMSESNRMSESNRMSESNRMSE7.5719.0428.539820.1022.341021.8514.942421.9214.7066-0.3913.22108.940014.0390.290015.9358.229516.0057.3045-4.5010.09223.681510.80189.973712.67123.530912.75121.3709
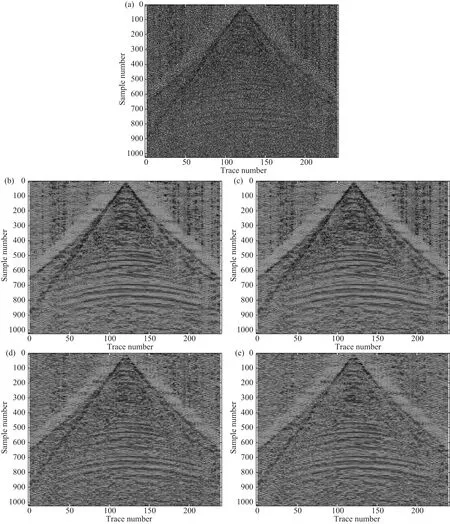
图5 实际地震信号降噪结果(a)实际地震信号;(b)本文方法1降噪后的地震信号;(c)本文方法2降噪后的地震信号;(d)DWT Bishrink降噪后的地震信号;(e)DTCWT Bishrink降噪后的地震信号.Fig.5 The denoised results of the field seismic signal(a)The field seismic signal;(b)The denoised seismic signal via the method 1;(c)The denoised seismic signal via the method 2;(d)The denoised seismic signal via the DWT Bishrink;(e)The denoised seismic signal via the DTCWT Bishrink.
由图4中的(a)—(c)子图可以看出,本文方法能够较好地压制随机噪声.从图4(b、c)振幅谱图中可看出,高频噪声得到了有效压制,且低频中混有的噪声也有所减弱.
综合表2和图4可以看出,本文方法在信噪比上较一些经典的降噪方法有一定的提高,而且降噪得到的地震信号与原地震信号具有更小的差异.压制随机噪声的同时较好地保留了地震信号的大部分细节信息.
7 实际地震资料处理
为了进一步测试本文方法对地震信号降噪的效果,采用DWT Bishrink方法、DTCWT Bishrink方法、本文方法1和本文方法2对实际采集的地震信号进行降噪处理,各小波分解层数均为4层.图5显示了实际地震信号降噪效果.
观察图5可知,本文提出的两种方法在压制随机噪声的同时也保留了更多的有效信号,具有较高的保真度.
8 结论
本文分析了地震信号经双树复小波变换后同一方向实部与虚部小波系数、实部(或虚部)系数与模的相关性.通过计算互信息进行验证,证实了实部与虚部系数、实部(或虚部)系数与模之间存在较强的相关关系.因此对小波系数实部与虚部、实部(或虚部)系数与模分别建立双变量模型,得到了两种地震信号随机噪声压制的双变量方法.本文方法不仅在信噪比上较一些经典的降噪算法有一定的提高,而且较好地保留了地震信号中的有效信息.当然本文方法还有需要进一步改进的地方,例如小波系数之间的相关性可以考虑采用其他统计模型进行分析,以获得更好的降噪效果.
致谢作者非常感谢两位匿名评审专家提出的宝贵意见.
References
Abdelnour A F,Selesnick I W.2001.Nearly symmetric orthogonal wavelet bases.//Proceedings of the IEEE International Conference on Acoustics,Speech,Signal Processing (ICASSP).IEEE.Berkner K,Wells R O Jr.2002.Smoothness estimates for soft-threshold denoising via translation-invariant wavelet transforms.Applied and Computational Harmonic Analysis,12(1):1-24,doi:10.1006/acha.2001.0366.
Coifman P R,Donoho D L.1995.Translation-invariant de-noising.//Wavelets and Statistics.New York:Springer,125-150.
Donoho D L,Johnstone J M.1994.Ideal spatial adaptation by wavelet shrinkage.Biometrika,81(3):425-455.
Hill P,Achim A,Bull D.2012.The Undecimated dual Tree Complex Wavelet Transform and its application to bivariate image denoising using a Cauchy model.//2012 19th IEEE International Conference on Image Processing (ICIP).Orlando,FL:IEEE,1205-1208.
Kingsbury N.1998.The dual-tree complex wavelet transform:A new technique for shift invariance and directional filters.//Proceedings of European signal processing Conference.Rhodes,319-322.Kingsbury N.2001.Complex wavelets for shift invariant analysis and filtering of signals.Applied and Computational Harmonic Analysis,10(3):234-253,doi:10.1006/acha.2000.0343.
Liu J,Moulin P.2001.Information-theoretic analysis of interscale and intrascale dependencies between image wavelet coefficients.IEEE Transactions on Image Processing,10(11):1647-1658,doi:10.1109/83.967393.
Liu X,He Z H,Huang D J.2006.Seismic data denoising research based on wavelet transform.Petroleum Geophysics (in Chinese),4(4):15-18.Luisier F,Blu T,Unser M.2007.A new SURE approach to image denoising:Interscale orthonormal wavelet thresholding.IEEE Transactions on Image Processing,16(3):593-606,doi:10.1109/TIP.2007.891064.
Peng H C,Long F H,Ding C.2005.Feature selection based on mutual information criteria of max-dependency,max-relevance,and min-redundancy.IEEE Transactions on Pattern Analysis and Machine Intelligence,27(8):1226-1238,doi:10.1109/TPAMI.2005.159.
Sendur L,Selesnick I W.2002.Bivariate shrinkage with local variance estimation.IEEE Signal Processing Letters,9(12):438-441,doi:10.1109/LSP.2002.806054
Shi F,Selesnick I W.2007.An elliptically contoured exponential mixture model for wavelet based image denoising.Applied and Computational Harmonic Analysis,23(1):131-151,doi:10.1016/j.acha.2007.01.007.
Wang Z G,Zhou X X,Li J.2002.Noise attenuation using minimum smooth filter based on wavelet transform.Oil Geophysical Prospecting (in Chinese),37(6):594-600.
Yin M,Liu W.2012.Image denoising using mixed statistical model in nonsubsampled Contourlet transform domain.Acta Photonica Sinica,41(6):751-756,doi:10.3788/gzxb20124106.0751.Yin M,Bai R F,Xing Y,et al.2014.Denoising algorithm by Nonsubsampled Dual-tree Complex Wavelet domain bivariate model.Acta Photonica Sinica (in Chinese),43(10):1010004,doi:10.3788/gzxb20144310.1010004.
Zhang B,Yin X Y,Wu G C,et al.1999.Random noise elimination using wavelet analysis and inversion.Oil Geophysical Prospecting (in Chinese),34(6):635-641.Zhang K,Liu G Z,Zou D W,et al.1996.Seismic data time-frequency Domain Denoising based on dyadic wavelet transform.Acta Geophysica Sinica (in Chinese),39(2):265-271.Zong T,Meng H Y,Jia Y L,et al.1998.Denoising method based on wavelet packet and forward-backward prediction in F-X domain.Acta Geophysica Sinica (in Chinese),41(S1):337-346.
附中文参考文献
刘鑫,贺振华,黄德济.2006.基于小波变换的地震资料去噪处理研究.油气地球物理,4(4):15-18.
王振国,周熙襄,李晶.2002.基于小波变换的最小光滑滤波去噪.石油地球物理勘探,37(6):594-600.
殷明,白瑞峰,邢燕等.2014.基于非下采样双树复小波域的双变量模型去噪算法.光子学报,43(10):1010004,doi:10.3788/gzxb20144310.1010004.
张波,印兴耀,吴国忱等.1999.用小波分析和反演方法联合去除随机噪声的研究.石油地球物理勘探,34(6):635-641.
章珂,刘贵忠,邹大文等.1996.二进小波变换方法的地震信号分时分频去噪处理.地球物理学报,39(2):265-271.
宗涛,孟鸿鹰,贾玉兰等.1998.小波包F-X域前后向预测去噪.地球物理学报,41(S1):337-346.
(本文编辑胡素芳)
Dual-tree complex wavelet domain bivariate method for seismic signal random noise attenuation
WANG Jin-Ju,YUAN Li,LIU Wan-Ru,XU Xiao-Hong
School of Mathematics,Hefei University of Technology,Hefei 230009,China
Seismic signal noise attenuation is important in processing and interpreting seismic signal subsequently.Two dual-tree complex wavelet domain bivariate methods for seismic signal random noise attenuation are proposed.After the dual-tree complex discrete wavelet transform,the real and imaginary parts of the wavelet coefficients have dependency in the same direction.The real or imaginary parts and the corresponding magnitudes of the wavelet coefficients have dependency in the same direction.So we construct the bivariate model for the real and imaginary parts in the same direction.Using the model the wavelet coefficients of the original seismic signal are estimated.The denoised seismic signal is achieved based on the dual-tree complex wavelet inverse transform.The proposed algorithm is also extended to the real or imaginary parts and the corresponding magnitudes of dual-tree complex wavelet coefficients in the same direction.Through experiments on the synthetic seismic record and the field seismic data,the results demonstrate that the proposed two methods can attenuate random noise effectively.
Dual-tree complex wavelet transform;Random noise;Bivariate model;Wavelet coefficients
汪金菊,袁力,刘婉如等.2016.地震信号随机噪声压制的双树复小波域双变量方法.地球物理学报,59(8):3046-3055,
10.6038/cjg20160827.
Wang J J,Yuan L,Liu W R,et al.Dual-tree complex wavelet domain bivariate method for seismic signal random noise attenuation.Chinese J.Geophys.(in Chinese),59(8):3046-3055,doi:10.6038/cjg20160827.
国家重大科研装备研制项目“深部资源探测核心装备研发”(ZDYZ2012-1)—06子项目“金属矿地震探测系统”—05课题“系统集成野外试验与处理软件研发”,中央高校基本科研业务费专项资金(J2014HGXJ0072,2015HGZX0018),国家级大学生创新创业训练计划项目(201410359075)共同资助.
汪金菊,女,1978年生,博士,讲师,主要从事信号处理等工作.E-mail:wjj@hfut.edu.cn
10.6038/cjg20160827
P631
2015-12-01,2016-01-19收修定稿
