一类三次微分系统的分段光滑扰动

李志鹏,　水树良

(浙江师范大学 数理与信息工程学院,浙江 金华　321004)



一类三次微分系统的分段光滑扰动

李志鹏,水树良

(浙江师范大学 数理与信息工程学院,浙江 金华321004)

考虑了一类具有二次不变曲线的平面三次微分系统在分段三次多项式扰动下的极限环个数问题.利用一阶Melnikov函数,证明了从该系统的周期环域可以分支出8个极限环.结果表明:分段三次多项式扰动此类三次微分系统比其相应的三次多项式扰动可多产生4个极限环.

极限环;不变曲线;一阶Melnikov函数；分段光滑系统

0　引　言

众所周知,Hilbert第16问题的后半部分是非常困难的公开问题,即便是Arnold给出的弱化形式也只解决了一些特殊情形[1].近年来,人们考虑如下形式的平面系统:

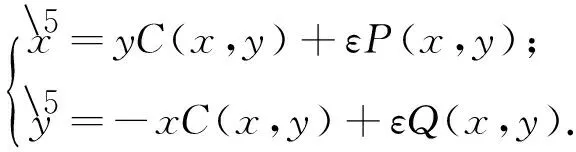
(1)

系统(1)中:ε是小参数;P(x,y),Q(x,y)是n次多项式;C(x,y)是m次多项式且C(0,0)≠0.当ε=0时,C(x,y)=0是系统(1)的不变代数曲线.在区域Ω={(x,y) |C(x,y)≠0}内,系统(1)的等价系统为近Hamilton系统

(2)

当ε=0时,系统(2)有一族闭轨Lh={(x,y) |H(x,y)=x2+y2=h},h∈(0,+∞).

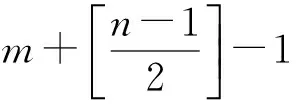
最近,对于光滑系统(1)的分支现象研究得比较多,但对于分段光滑微分系统

(3)

的研究少见报道.文献[7]利用一阶平均理论,给出了“当C(x,y)=1+x时,系统(3)有5个极限环”的结论,比相应的光滑微分系统多分支出3个极限环.本文利用一阶Melnikov函数,研究了当C(x,y)=(1-x)2时系统(3)的极限环个数问题.

考虑如下分段光滑三次微分系统:

(4)

系统(4)中:

易知未扰系统(4)在x>0和x≤0时具有相同的首次积分H(x,y)=x2+y2.

本文的主要目标是计算从未扰系统(4)|ε=0原点的周期环域分支出极限环的个数.所用的方法是文献[8]中介绍的一阶Melnikov函数.

定理1当|ε|>0充分小时,系统(4)经扰动后从未扰动系统的周期轨分支出8个极限环.

文献[8]考虑了平面分段近Hamilton系统

(5)

系统(5)中:0<ε≪1;H±∈C∞;f±(x,y)∈C∞;g±(x,y)∈C∞.对系统(5)作以下假设：

(H1)存在区间J=(h1,h2),系统 (5)|ε=0有一族顺时针周期轨道L(h):H(x,y)=h,h∈J;

(H2)各周期轨道交y轴于不同的两点A(h)=(0,a(h))和A1(h)=(0,b(h)),其中a(h)>0,b(h)<0.

在假设(H1)和(H2)下,根据文献[8]定理1.1和文献[9]引理2.2,可以得到系统(5)的一阶Melnikov函数为

(6)

此时,确定系统(5)的极限环个数就转化为求一阶Melnikov函数M(h)孤立零点个数(重根按重数计算)的问题.

1　定理1的证明

在证明定理1之前,先给出一个引理.

引理1[10]如果函数F1,F2,…,Fn在实数R上是线性无关的,那么存在b1,b2,…,bn和β1,β2,…,βn,有

系统(4)等价于分段光滑近Hamilton系统

(7)

系统(7)有一族周期轨道L(h)=x2+y2=h,h∈(0,1).由式(6)知

(8)

式(8)中,

(9)

对于式(9),运用Green′s公式可得

通过计算,M+(h)可以化简为

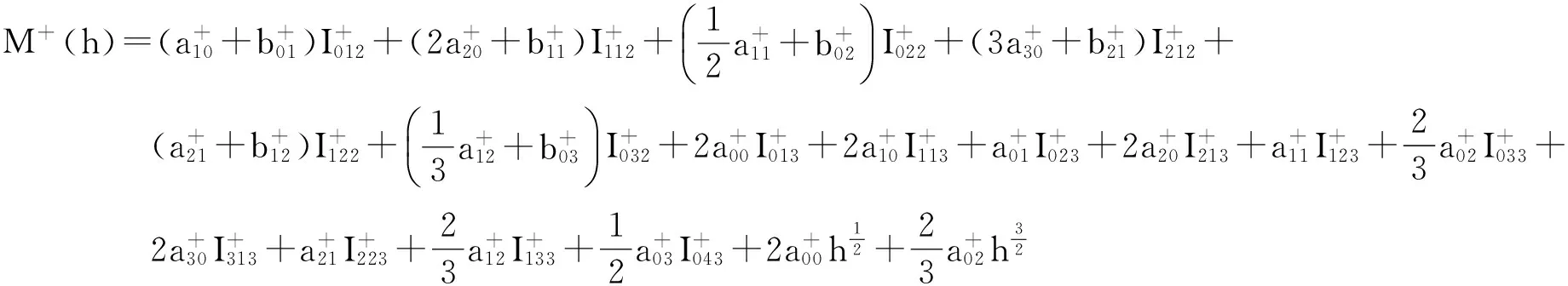
(10)

式(10)中,

(11)

李丽送走师兄后，又想到毕业了的师兄师姐很多，而在自己毕业的时候，这些师兄师姐已经工作很多年了，大部分都已经是公司的中层领导了，到时候如果有他们的帮助，肯定能找到一份好工作。李丽很快找到了大部分师兄师姐的联系方式，然后逐个去联系。

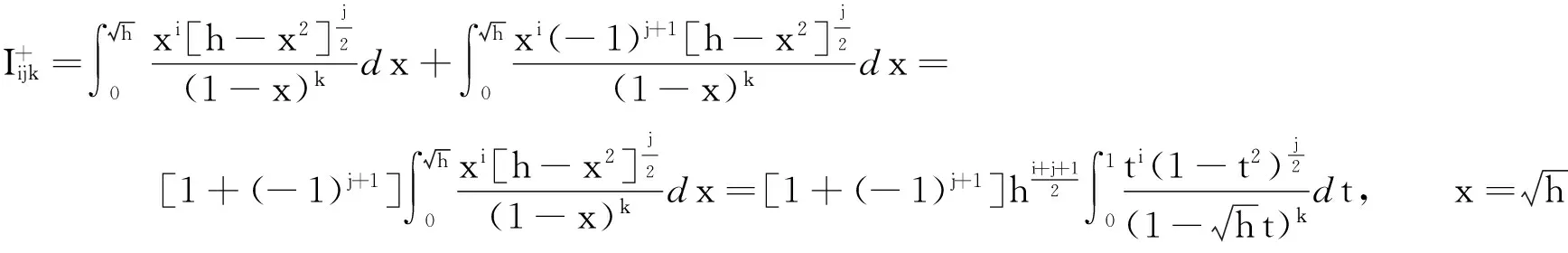
用相同的方法得到

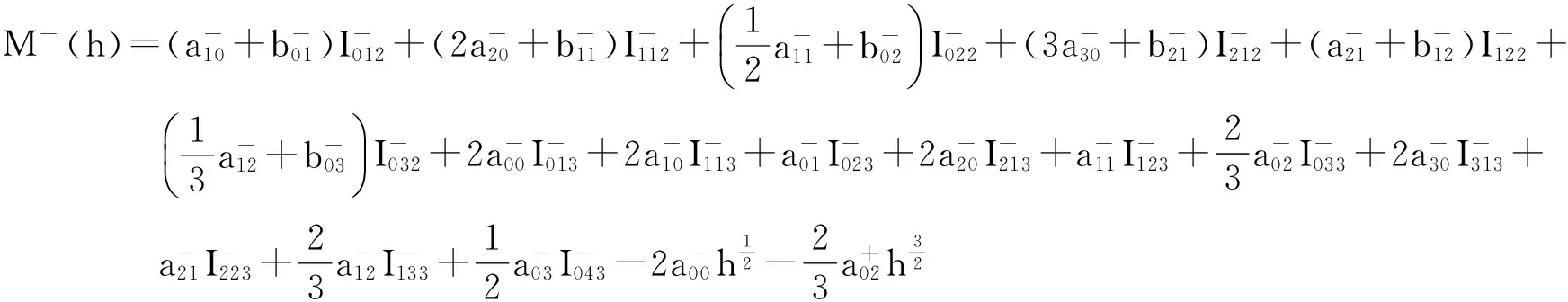
(12)

式(12)中,

(13)

C7G7(h)+C8G8(h)+C9G9(h)+C10G10(h).

(14)

式(14)中:

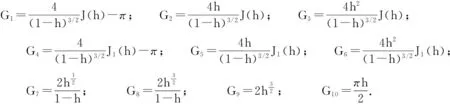
2　结　语

在系统(1)中,选取不同的C(x,y)会影响系统(1)的极限环的个数.到目前为止,对此已经有了一些研究成果.但对于分段光滑系统(3)的研究还不多,因此,可以选取不同的C(x,y)来研究系统(3)的分支现象.

[1]LiJB.Hilberts16thproblemandbifurcationsofplanarpolynomialvectorfields[J].IntJBifurChaosApplSciEng,2003,13(1):47-106.

[2]LlibreJ,RioJSPD,RodriguezJA．Averaginganalysisofaperturbedquadraticcenter[J]．NonliearAnal,2001,46(1)：45-51．

[3]LiuChao,HanMaoan.Thenumberoflimitcyclesofapolynomialsystemontheplane[J].AbstrApplAnal,2013,2013(2013):634-656.

[4]WangJing,ShuiShuliang.Poincarébifurcationoftwoclassesofpolynomialsystems[J].AbstrApplAnal,2013,2013(2013):1-12.

[5]YaoHY,HanMA．Thenumberoflimitcyclesofaclassofpolynomialdifferentialsystems[J]．NonlinearAnal,2012,75(1)：341-357．

[6]XiangGH,HanMA.Globalbifurcationoflimitcyclesinafamilyofmutiparametersystem[J].InternatJBifurChaos,2004,14(9)：3325-3335.

[7]李时敏,赵育林,岑秀丽.一类不连续平面二次微分系统的极限环[J].中国科学:A辑 数学,2015,45(1):43-52.

[8]LiuX,HanMA.BifurcationoflimitcyclesbyperturbingpiecewiseHamiltoniansystems[J].InternatJBifurChaosApplSciEng,2010,20(5):1379-1390.

[9]LiangF,HanMA.Limitcyclesneargeneralizedhomoclinicanddoublehomoclinicloopsinpiecewisesmoothsystems[J].ChaosSolitonsFractals,2012,45(4):454-464.

[10]LlibreJ,SwirszcaG.Onthelimitcyclesofpolynomialvectorfields[J].DynContinDiscreteImpulsSystSerA:MathAnal,2011,18(2):203-214.

(责任编辑陶立方)

Piecewise smooth perturbation for a class of cubic differential systems

LI Zhipeng,SHUI Shuliang

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,Jinhua321004,China)

It was studied the number of limit cycles that bifurcated from the periodic solutions of a cubic differential system, when it was perturbed by piecewise cubic polynomials. By using first order Melnikov functions to this system, it was proved that 8 limit cycles were bifurcated from the period annulus. The result showed that piecewise cubic polynomials perturbation cubic differential system had 4 more limits cycles than corresponding cubic polynomials perturbation.

limit cycles; invariant curve; first order Melnikov functions; piecewise smooth systems

10.16218/j.issn.1001-5051.2016.03.004

收文日期：2015-11-22；2015-12-29

国家自然科学基金资助项目(11171309;11172269)

李志鹏(1988-),男,河南周口人,硕士研究生.研究方向:微分方程与动力系统.

水树良.E-mail: shuisl@zjnu.cn

O175.25

A

1001-5051(2016)03-0258-05