自内射代数上的d-Koszul代数
2016-09-29吕家凤
吕家凤, 王 雪
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
自内射代数上的d-Koszul代数
吕家凤,王雪
(浙江师范大学 数理与信息工程学院,浙江 金华321004)
主要引入了自内射d-Koszul代数的概念,研究了它的一些基本性质.运用反证法和数学归纳法等方法得到了2个主要结果:一是证明自内射d-Koszul代数是d-齐次代数;二是证明自内射d-Koszul复形恰好是其平凡模的一个极小分次投射分解.因此,得到了自内射d-Koszul代数与经典的d-Koszul代数具有很多类似性质的结论.
自内射d-Koszul代数;d-齐次代数;复形;投射分解
0 引 言
Koszul代数最初由Priddy于1970年正式提出,经过40多年的研究,Koszul代数出现了各种形式的推广:纯分解的、非纯分解的等.特别地,最近,对于分次代数A,当A0不是半单时,文献[1-5]给出了更为广泛的Koszul理论.本文采用文献[2]的思想方法,把文献[6]中的d-Koszul代数推广到零次分支非半单的分次代数的情形,引入了所谓的自内射d-Koszul代数,即分次代数A=A0⊕A1⊕A2⊕…的零次分支A0是自内射的k-代数.通过反证法和数学归纳法等相关方法,证明了自内射d-Koszul代数是d-齐次代数;通过研究自内射d-Koszul代数的复形,证明了该复形恰好是其平凡模A0的一个极小分次投射分解.这些结果是自内射d-Koszul代数的基本性质,为进一步研究这类代数的结构和更深层次的性质奠定了基础.
1 预备知识
首先回顾一些本文将要用到的定义及相关预备知识.
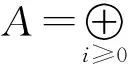
使得每个分次投射模Pi都是由δ(i)次生成,则称M为自内射d-Koszul模.其中,
特别地,若A0作为分次A-模是自内射d-Koszul模,则称A是自内射d-Koszul代数.
引理1设M是生成次数为s的分次A-模.如果Ms是投射的A0-模,那么
其中,ΩM是M的第1个合冲.
证明当i>1时,M的线性投射分解为
若将函子Hom(-,A0)作用到M的线性投射分解中,可以得到如下的复形:
则
又因为ΩM的投射分解为
且依然将函子Hom(-,A0)作用到ΩM的投射分解中,得到复形
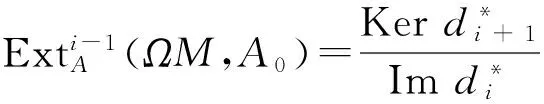
当i=1时,将函子Hom(-,A0)作用到短正合序列0→ΩM→P→M→0中,得到下面的正合序列:
因为P为M的分次投射盖,M的生成次数为s,所以P的生成次数也为s.又因Ms是投射的A0-模,Ps≅Ms,所以

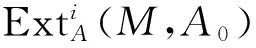

证明若A是自内射d-Koszul代数,则A0是自内射d-KoszulA-模,从而Ωi(A0)δ(i)是投射的A0-模.此外,存在A0的极小分次投射分解
其中,Pi由δ(i)次生成.将函子HomA(-,A0[n])作用到A0的极小分次投射分解中,可以得到复形
当n=δ(i)时,HomA(Pi,A0[n])≠0;当n≠δ(i)时,HomA(Pi,A0[n])=0.若考虑复形
则

反之,要证分次代数A是自内射d-Koszul代数,即证A0是自内射d-KoszulA-模.又因为A0是自内射d-KoszulA-模与Ωi(A0)的生成次数为δ(i)是等价的,所以只需证Ωi(A0)的生成次数为δ(i).
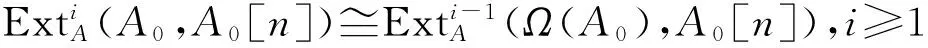
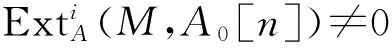
现在来回顾由A1生成的张量代数T(A),它是(A0,A0)-双模,即
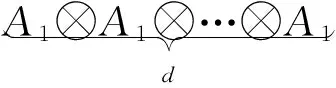
2 主要结论及证明
定理1如果A是自内射d-Koszul代数,那么A是d-齐次代数.
证明首先考虑下面的正合序列:


由于m(p(x))=0,所以p(x)∈W.下面证明p(x)∉JW.

由于A0是自内射d-KoszulA-模,所以J[-δ(1)]=Ω(A0)[-δ(1)],即J[-1]=Ω(A0)[-1].可知A1≅J[-1]0是投射的A0-模,故下面的序列也是正合的:
因为p(x-y)=0,所以x-y∈Rn-1⊗A1,进而可得x∈Rn-1⊗A1+y,即x∈Rn-1⊗A1+A1⊗Rn-1,得到矛盾.因此,p(x)∉JW.
综上可知,p(x)∈W/JW≅Wδ(2)的生成次数为δ(2).但是,由于p作为一个分次同态,x∈Rn,n>2,对任意的n是矛盾的,所以A是d-齐次代数.定理1证毕.
现在介绍A的自内射d-Koszul复形.
设A≅T(A)/(R)是d-齐次代数,其中,R是某些d次齐次元所生成的理想,定义

定理2若A≅T(A)/(R)是一个d-齐次代数,则A是自内射d-Koszul代数当且仅当自内射d-Koszul复形是A0的投射分解.
证明若A是自内射d-Koszul代数,则A0是自内射d-KoszulA-模,从而,A的自内射d-Koszul复形K*有以下性质:
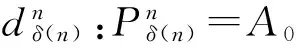



下证复形是正合的.
由序列
是右正合的可知,结论对n=1是成立的.当n>1时,
又因A0是d-KoszulA-模,且由引理2可知,只有当m=δ(n+1)时,
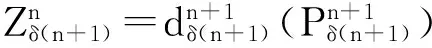
反之显然.定理2证毕.
[1]LiLiping.AgeneralizedKoszultheoryanditsrelationtotheclassicaltheory[J].JAlgebra,2014,420:217-241.
[2]LiLiping.AgeneralizedKoszultheoryanditsapplication[J].TransAmerMathSoc,2014,366(2):931-977.
[3]MadsenD.Ext-algebrasandderivedequivalences[J].ColloquiumMathematicsWarsaw,2006,104(1):113-140.
[4]MadsenD.OnacommongeneralizationofKoszuldualityandtiltingequivalence[J].AdvMath,2011,227(6):2327-2348.
[5]WoodcockD.Cohen-MacaulaycomplexesandKoszulrings[J].JLondonMathSoc,1998,57(2):398-410.
[6]GreenEL,MarcosEN,Martinez-VillaR,etal.d-Koszulalgebras[J].JPureApplAlgebra,2004,193(1):141-162.
(责任编辑陶立方)
d-Koszul algebra over self-injective algebra
LÜ Jiafeng,WANG Xue
(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,Jinhua321004,China)
The notion of self-injective algebra was introduced and some related properties of such algebras were studied. By using the reduction to absurdity and mathematical induction, it was proved that (1) self-injectived-Koszul algebras wered-homogeneous graded algebras; and (2) the self-injectived-Koszul complex was a minimal graded projective resolution of the trivialA-moduleA0. Therefore, it was concluded that self-injective algebras had many similar properties as classicd-Koszul algebras.
self-injectived-Koszul algebra;d-homogeneous algebra; complex; projective resolution
10.16218/j.issn.1001-5051.2016.03.003
收文日期:2016-01-02;2016-03-09
国家自然科学基金资助项目(11571316);浙江省自然科学基金资助项目(LY16A010003)
吕家凤(1980-),男,安徽定远人,副教授.研究方向:非交换代数.
O175.25
A
1001-5051(2016)03-0253-05
